Similar presentations:
Постоянный электрический ток. (Лекция 5)
1. Лекция 5
Постоянный электрический ток.2. Постоянный электрический ток
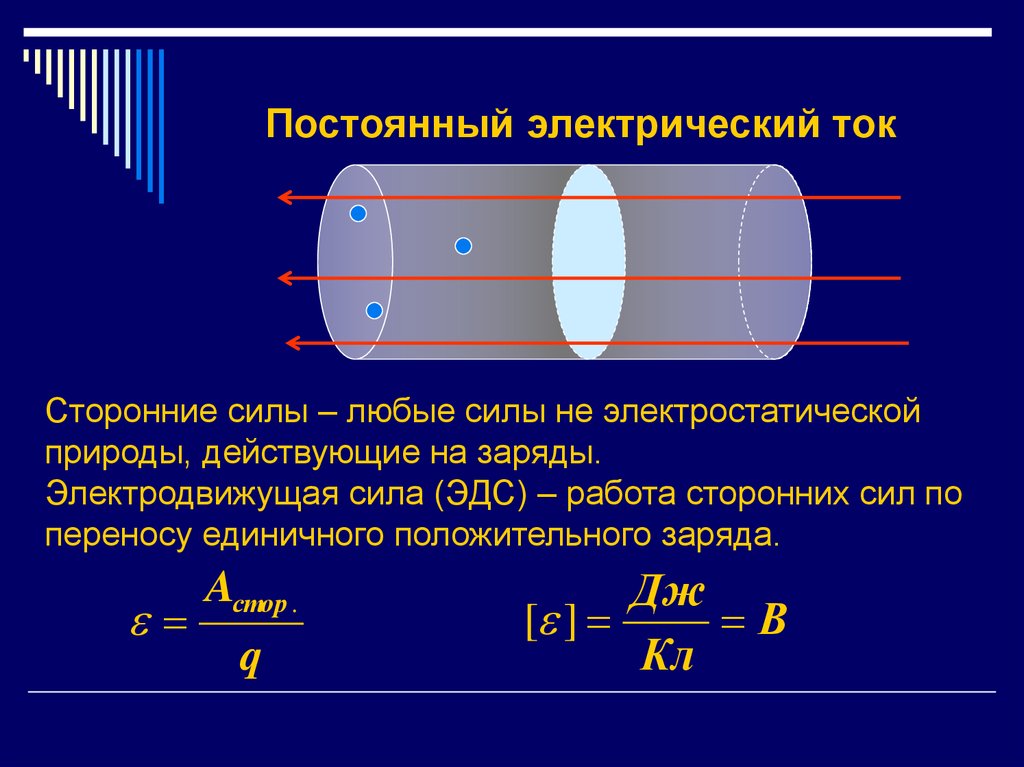
SЭлектрический ток – упорядоченное движение заряженных частиц.
Сила тока
Плотность тока
dq
I
dt
dI
j
n
dS
I A
А
j 2
м
3. Постоянный электрический ток
Сторонние силы – любые силы не электростатическойприроды, действующие на заряды.
Электродвижущая сила (ЭДС) – работа сторонних сил по
переносу единичного положительного заряда.
Aстор .
q
Дж
[ ]
В
Кл
4. Напряжение
– работа всех сил по переносу единичногоположительного заряда
U
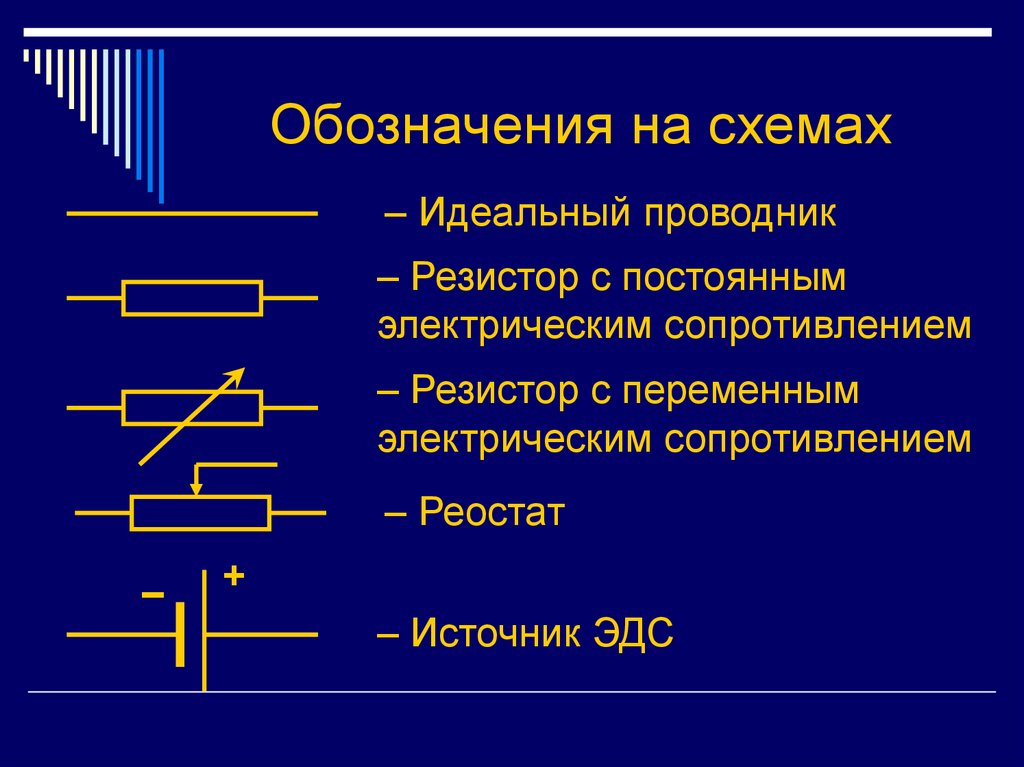
5. Обозначения на схемах
– Идеальный проводник– Резистор с постоянным
электрическим сопротивлением
– Резистор с переменным
электрическим сопротивлением
– Реостат
–
+
– Источник ЭДС
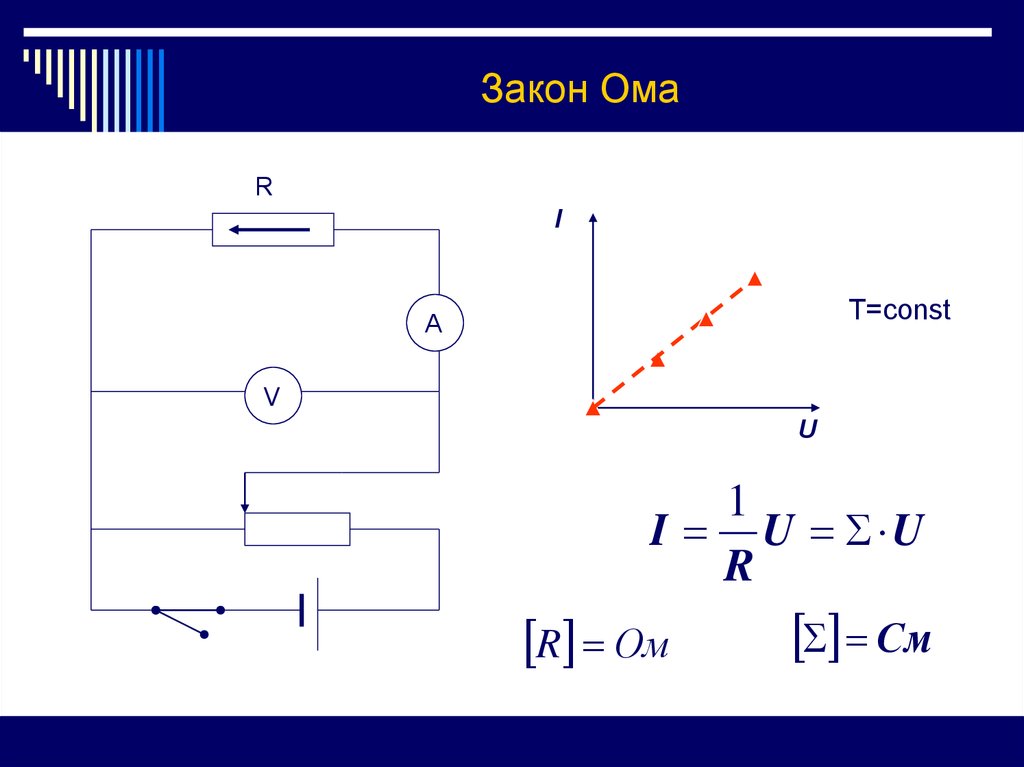
6. Закон Ома
RI
I
1
U
R
А
R
l
S
Т=const
V
U
R
l
S
1
I U U
R
R Ом
Cм
7. Закон Ома
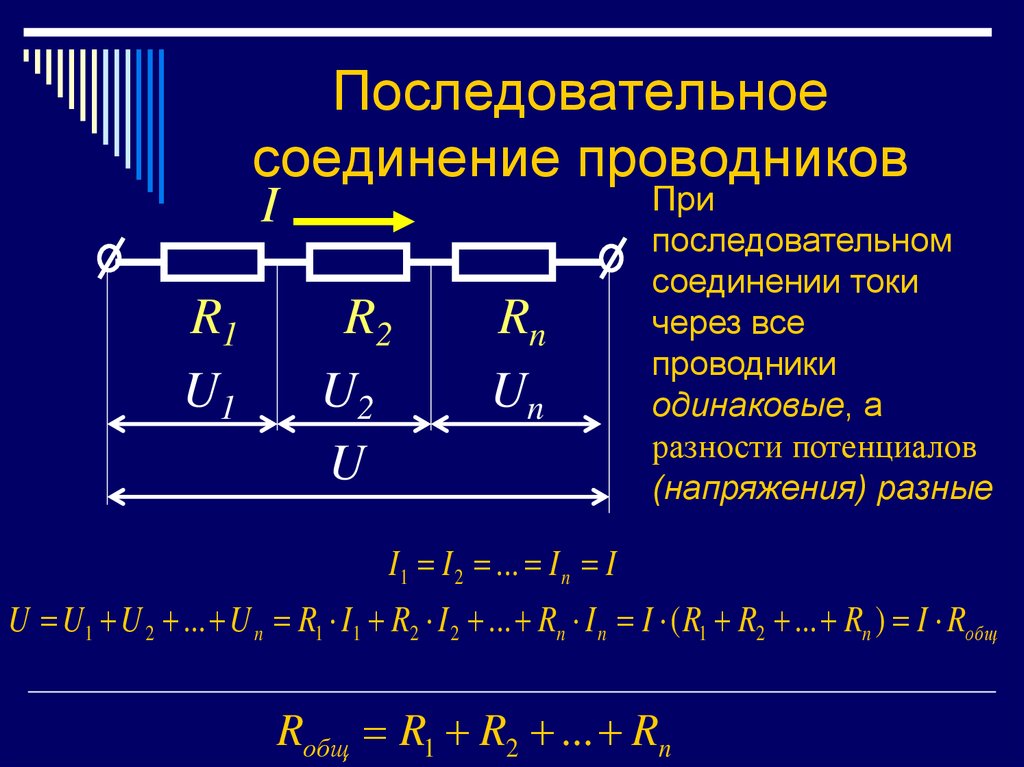
8. Последовательное соединение проводников
IR1
U1
R2
U2
U
Rn
Un
При
последовательном
соединении токи
через все
проводники
одинаковые, а
разности потенциалов
(напряжения) разные
I1 I 2 ... I n I
U U1 U 2 ... U n R1 I1 R2 I 2 ... Rn I n I ( R1 R2 ... Rn ) I Rобщ
Rобщ R1 R2 ... Rn
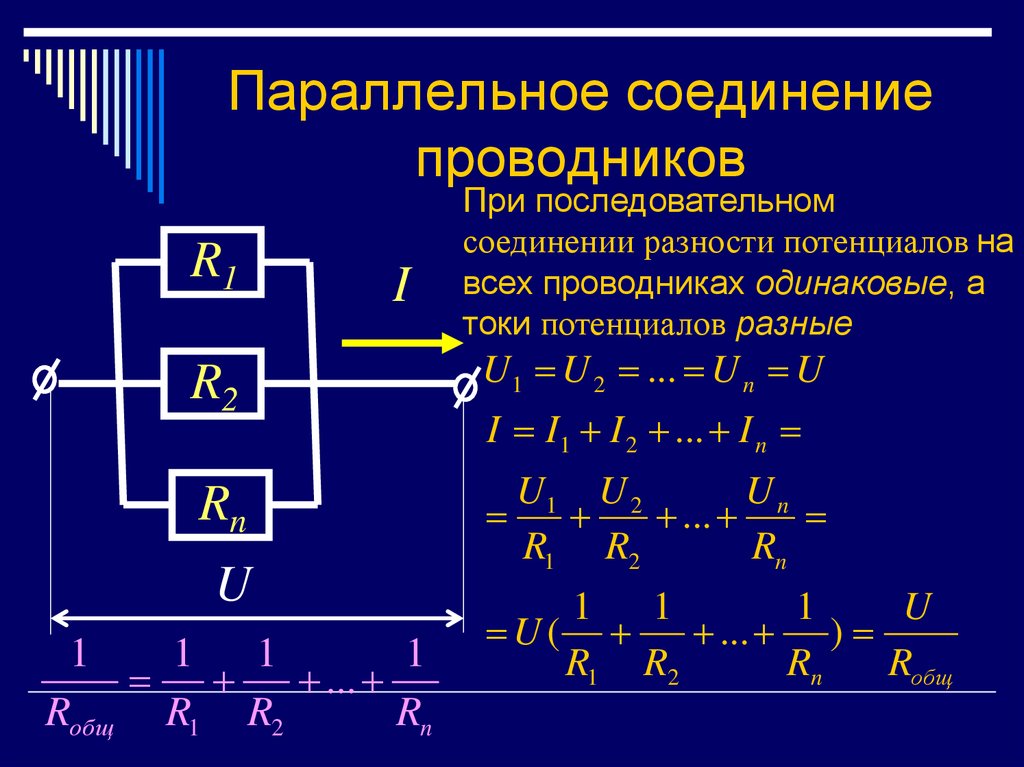
9. Параллельное соединение проводников
R1I
R2
Rn
U
1
1
1
1
...
Rобщ R1 R2
Rn
При последовательном
соединении разности потенциалов на
всех проводниках одинаковые, а
токи потенциалов разные
U1 U 2 ... U n U
I I1 I 2 ... I n
Un
U1 U 2
...
R1 R2
Rn
1
1
1
U
U(
... )
R1 R2
Rn
Rобщ
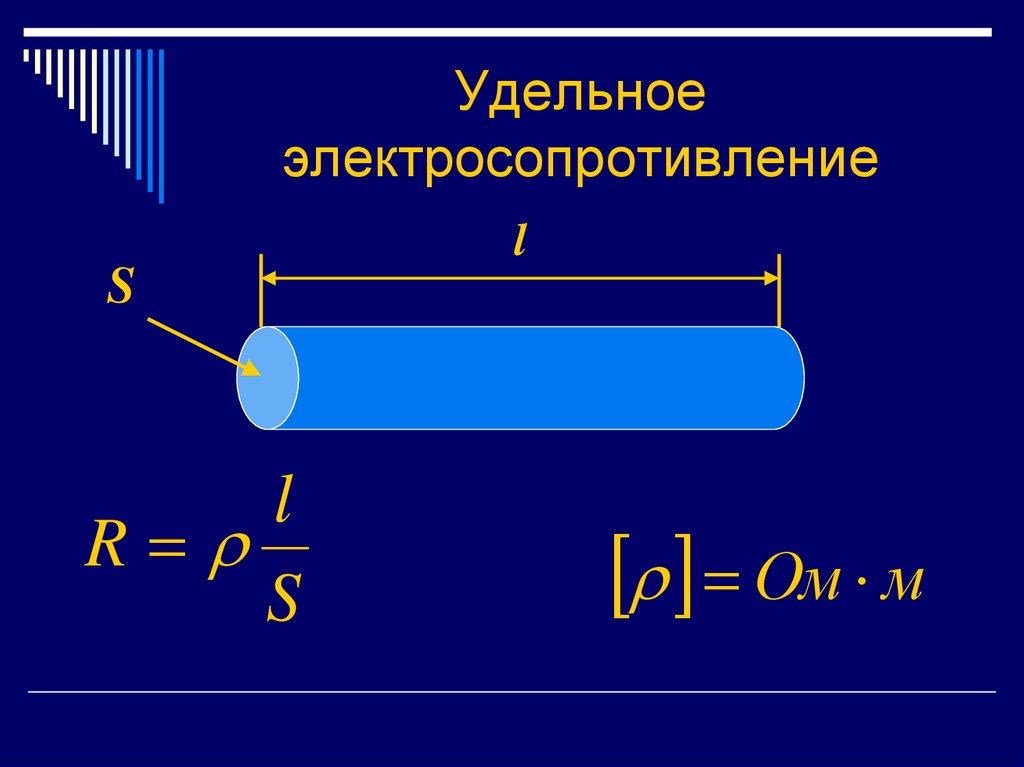
10. Удельное электросопротивление
lS
l
R
S
Ом м
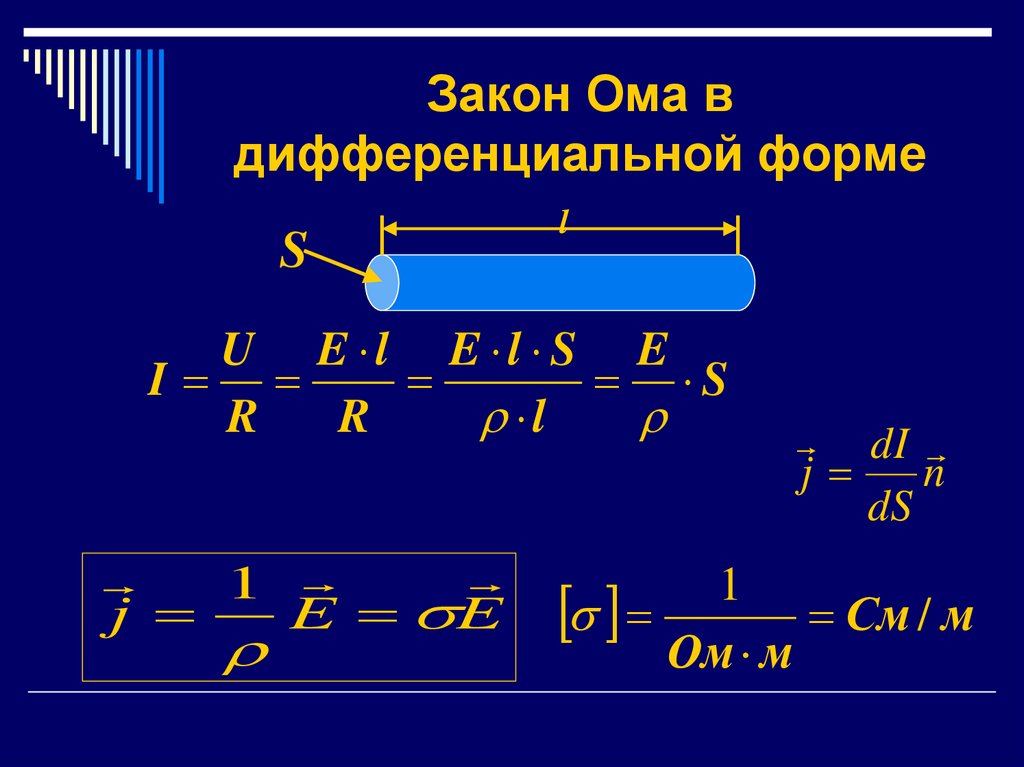
11. Закон Ома в дифференциальной форме
Sl
U E l E l S E
I
S
R
R
l
1
j
E E
dI
j
n
dS
1
См / м
Ом м
12. Закон Джоуля-Ленца
Интегральная формаРабота тока
A q U I U t
Мощность тока
A
P I U
t
Тепло, выделяемое в проводнике
P I R
2
Q I Rt
2
Q
I R t j S l
Q уд
V t
V t
S S l
2
Дифференциальная форма
2
2
Qуд j E
2
2
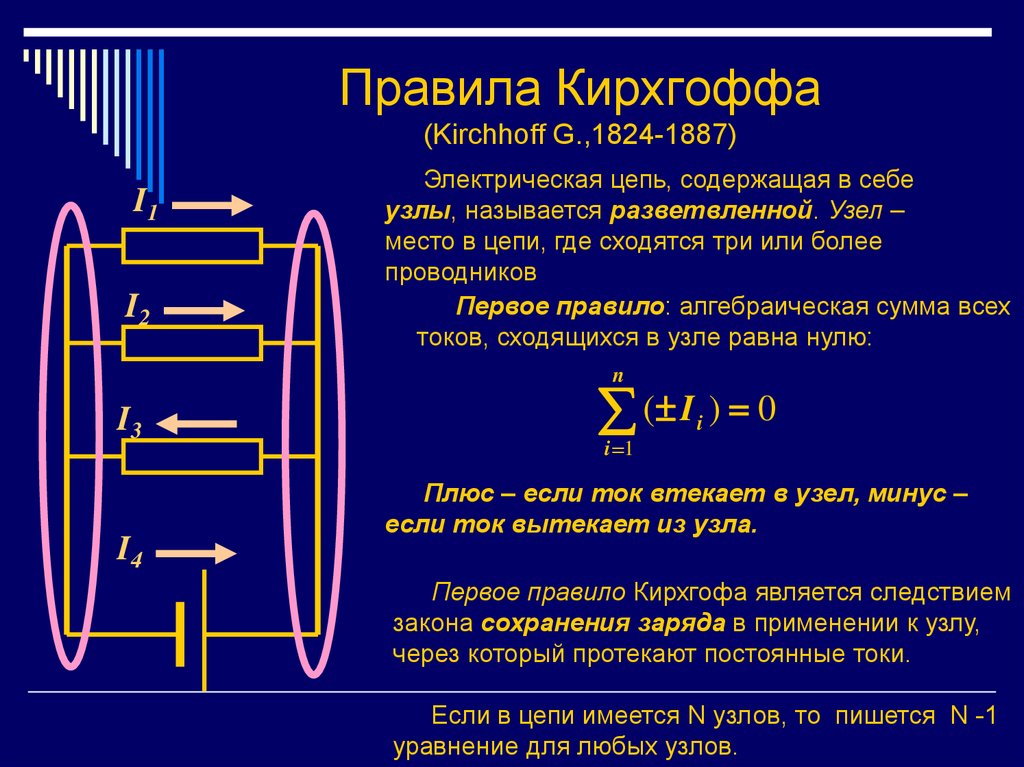
13. Правила Кирхгоффа (Kirchhoff G.,1824-1887)
I1I2
Электрическая цепь, содержащая в себе
узлы, называется разветвленной. Узел –
место в цепи, где сходятся три или более
проводников
Первое правило: алгебраическая сумма всех
токов, сходящихся в узле равна нулю:
n
I3
I4
( I ) 0
i 1
i
Плюс – если ток втекает в узел, минус –
если ток вытекает из узла.
Первое правило Кирхгофа является следствием
закона сохранения заряда в применении к узлу,
через который протекают постоянные токи.
Если в цепи имеется N узлов, то пишется N -1
уравнение для любых узлов.
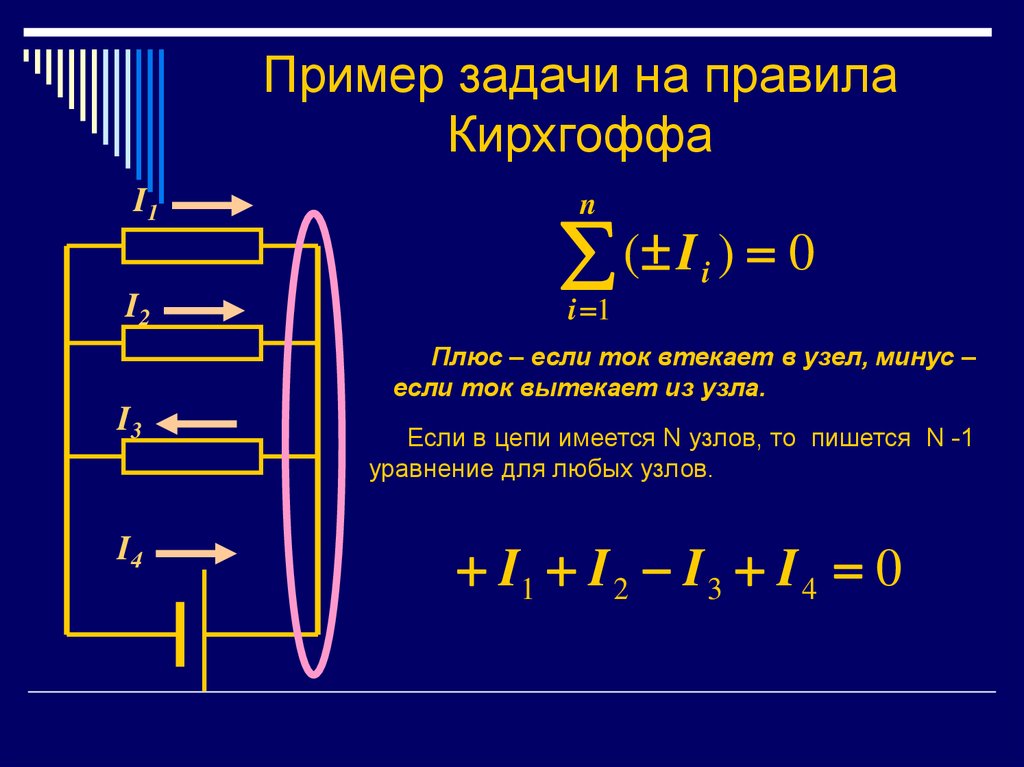
14. Пример задачи на правила Кирхгоффа
I1I2
n
( I ) 0
i 1
i
Плюс – если ток втекает в узел, минус –
если ток вытекает из узла.
I3
I4
Если в цепи имеется N узлов, то пишется N -1
уравнение для любых узлов.
I1 I 2 I 3 I 4 0
15. Правила Кирхгоффа (Kirchhoff G.,1824-1887)
I1I2
I3
I4
Второе правило: для любого замкнутого контура,
выделенного внутри разветвленной цепи,
алгебраическая сумма падений напряжений на
сопротивлениях равна алгебраической сумме ЭДС,
действующих в этом контуре:
n
m
( I R ) (
i 1
i
i
Плюс – если направление
тока совпадает с
направлением обхода.
k 1
k
)
Плюс – если направление
от минуса к плюсу
совпадает с
направлением обхода.
Второе правило Кирхгофа является следствием
равенства нулю циркуляции электростатического
поля по замкнутому контуру, то есть следствием его
потенциальности.
Если в цепи имеется M токов (ветвей) и N узлов, то
пишется M – (N -1) уравнение для любых контуров.
16.
Пример задачи на правилаКирхгоффа
I1
I2
I3
I4
n
m
( I R ) (
i 1
i
i
k 1
k
)
Плюс – если направление
Плюс – если направление
от минуса к плюсу
тока совпадает с
совпадает с
направлением обхода.
направлением обхода.
I1 R1 I 4 r k
Если в цепи имеется M токов (ветвей) и N узлов, то
пишется M – (N -1) уравнение для любых контуров.
I1 R1 I 2 R2 0
I 2 R2 I 3 R3 0
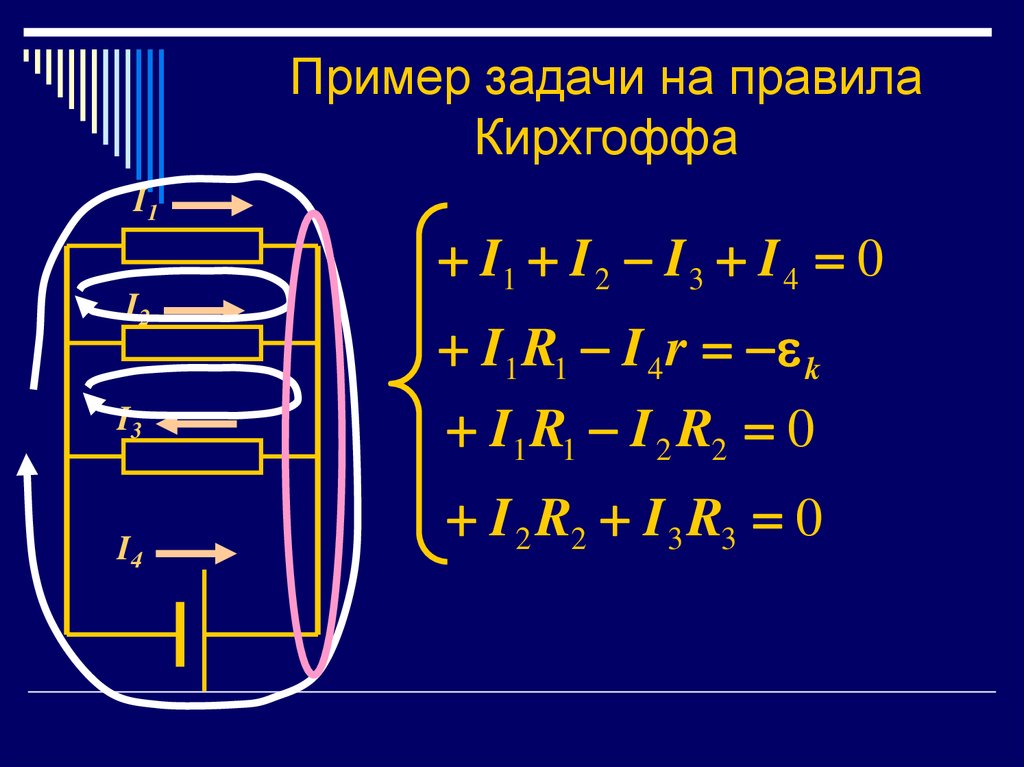
17.
Пример задачи на правилаКирхгоффа
I1
I2
I3
I4
I1 I 2 I 3 I 4 0
I1 R1 I 4 r k
I1 R1 I 2 R2 0
I 2 R2 I 3 R3 0
18.
LorentzHendrik
1853-1928
Drude
Paul Karl Ludwig
1863-1906
Основы классической
теории
электропроводности
металлов
(модель Друде – Лоренца,
1900 г.)
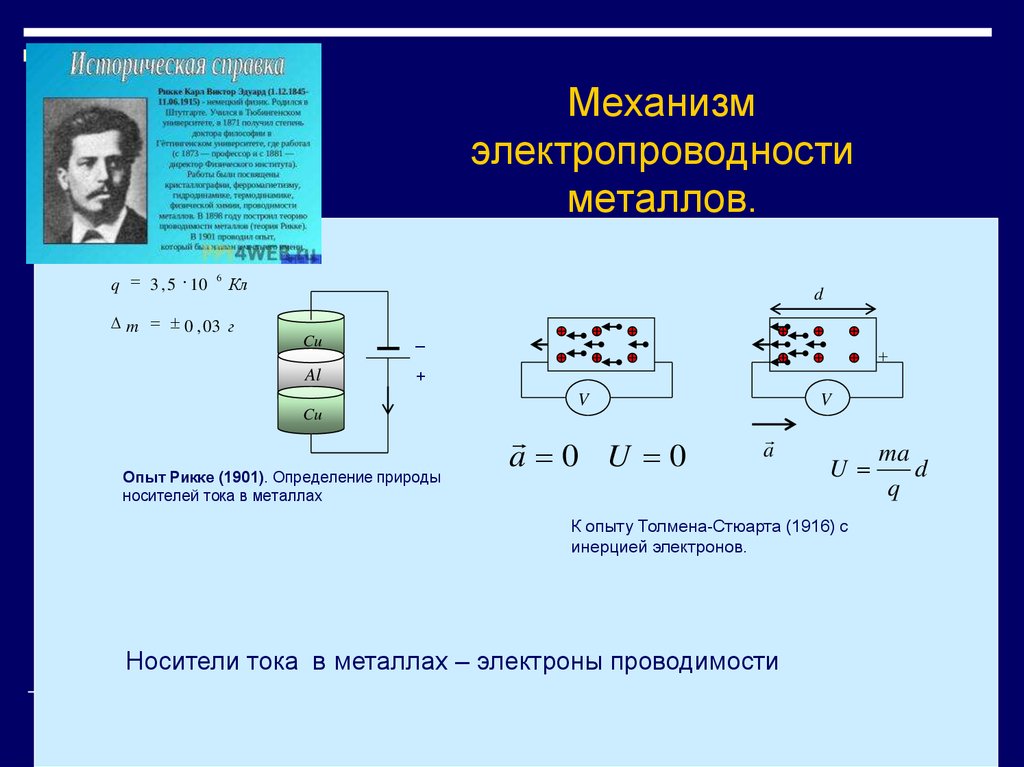
19. Механизм электропроводности металлов.
q 3 , 5 106
Кл
m 0 , 03 г
d
Cu
_
Al
+
Cu
Опыт Рикке (1901). Определение природы
носителей тока в металлах
_
V
a 0 U 0
V
a
U
К опыту Толмена-Стюарта (1916) с
инерцией электронов.
Носители тока в металлах – электроны проводимости
ma
d
q
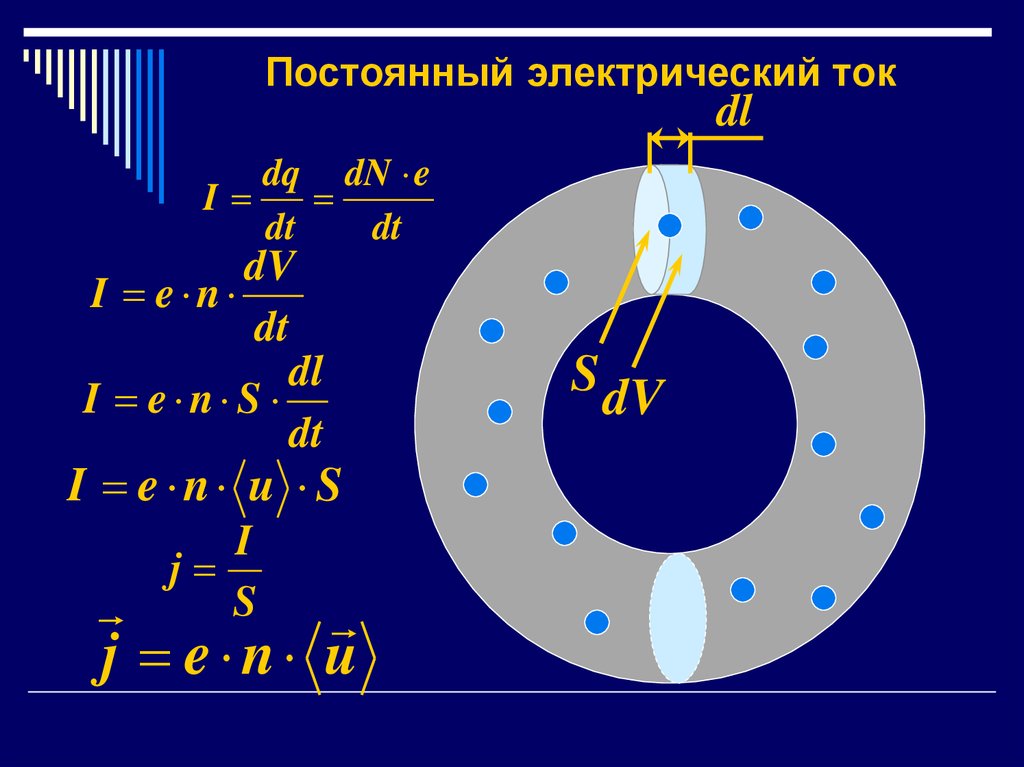
20. Постоянный электрический ток
dldq dN e
I
dt
dt
dV
I e n
dt
dl
I e n S
dt
I e n u S
I
j
S
j e n u
S dV
21. Оценка средней скорости кооперативного движения электронов проводимости
j e n un
N электронов
nCu
V
j
u
e n
N атомов zвалентност ь m металла z плотность z N A
V
mатома V
8,9 103 1 6 10 23
29
3
0
,
8
10
м
63,5 10 3
u
jmax
107
3 м
10
19
29
1,6 10 0,8 10
с
А
10 2
м
7
22. Основные положения классической теории проводимости Друде –Лоренца.
Основные положения классическойтеории проводимости Друде –
Лоренца.
1. Носители заряда – электроны, движение которых
подчиняется законам классической механики.
2. Можно не учитывать столкновения электронов
друг с другом. Взаимодействие с ионами – упругие
столкновения.
3. Поведение электронов подобно поведению
молекул идеального газа (электронный газ)
Средняя скорость хаотического движения электронов
8kT
v
105 м / с
m
v u
23. Движение заряда в электрическом поле
E24. Закон Ома в дифференциальной форме
_eE
F ma eE a
m
v
j en u
j E
eE
umax a
m
eE
u
2m v
ne 2
2m v
Е
eE
u
2m
1/
2m v
ne 2
25. Закон Джоуля–Ленца в дифференциальной форме
Кинетическая энергия, передающаяся иону:Общее число столкновений электронов
с ионами в единицу времени
Q уд E кин N
Q уд Е
2
me 2 2 E 2
2m 2 v
2
Wкин
2
mu max
2
N n
v
ne 2
n
E2
2m v
v
Q уд j
2
26. Длина свободного пробега
2m vne
2
плотность z N A
n
Медь: Cu
2m v
ne
2
2 m v
плотность z N A e 2
2 9,1 10 31 105 63,5 10 3
9
5
10
м
3
23
19 2
9
8,9 10 1 6 10 (1,6 10 ) 17 10
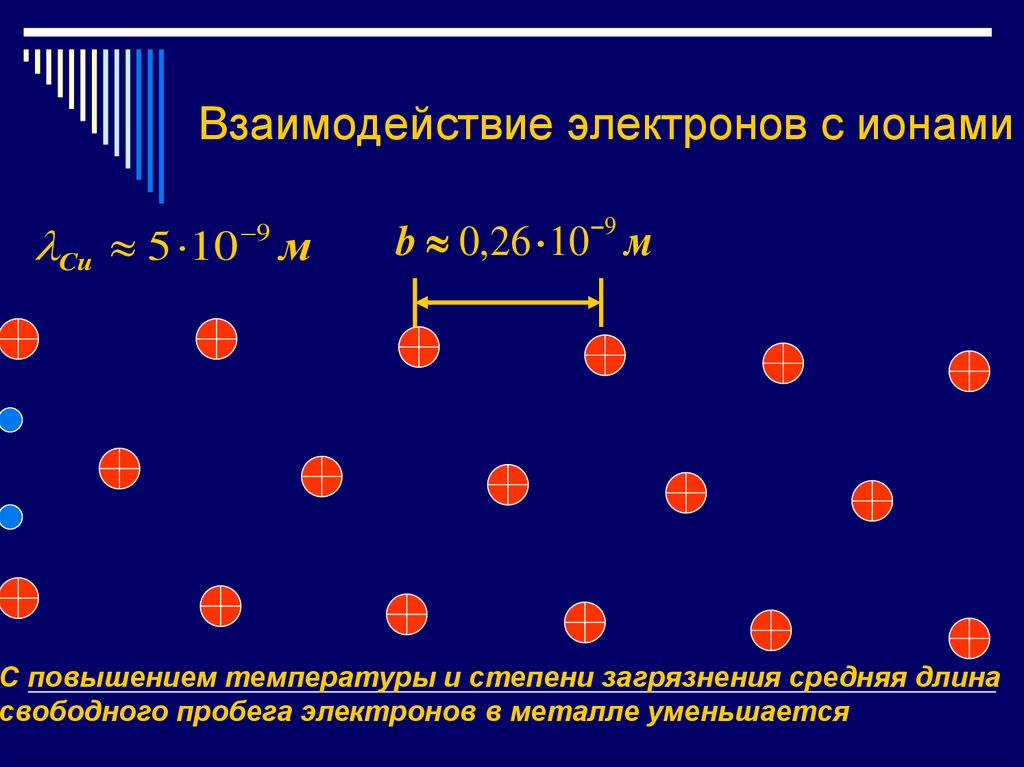
27. Взаимодействие электронов с ионами
Cu 5 10 м9
9
b 0,26 10 м
С повышением температуры и степени загрязнения средняя длина
свободного пробега электронов в металле уменьшается
28. Зависимость сопротивления металлов от температуры. Открытие сверхпроводимости (Г.Камерлинг-Онесс, 1911 г.)
1 - металл с примесями2 - чистый металл или интерметаллид
1
2
Тк
Т
Зависимость сопротивления металлов от температуры
в широком диапазоне температур вблизи Т= 300 К: R~T
Тк – температура
перехода в
сверхпроводящее
состояние
Вещество
Тк (К)
Титан
Алюминий
Ртуть
Свинец
0,4
1,2
4,1
7,2
29. Трудности классической теории
теорияВозможность
сверхпроводимости
только при Т=0
С=9/2 R
эксперимент
Наличие
сверхпроводимости
при Т≠0
С=3R
Объяснение сверхпроводимости дано в 1967 г. Дж.
Бардиным, Л. Купером, Дж. Шриффером (США) на
основе квантовой теории.
30. Высокотемпературная сверхпроводимость керамик
Высокотемпературная сверхпроводимость –1986-1987 г.г.
Дж. Беднорц, К.А.Мюллер, М. Такашиге.
Металлоксиды (оксиды лантана, бария, др.
элементов)
Температура перехода в сверхпроводящее
состояние ~ 100 К.















 physics
physics








