Примеры расчета рамы с распределенной массой на собственные и вынужденные колебания

1. Лекция Примеры расчета рамы с распределенной массой на собственные и вынужденные колебания

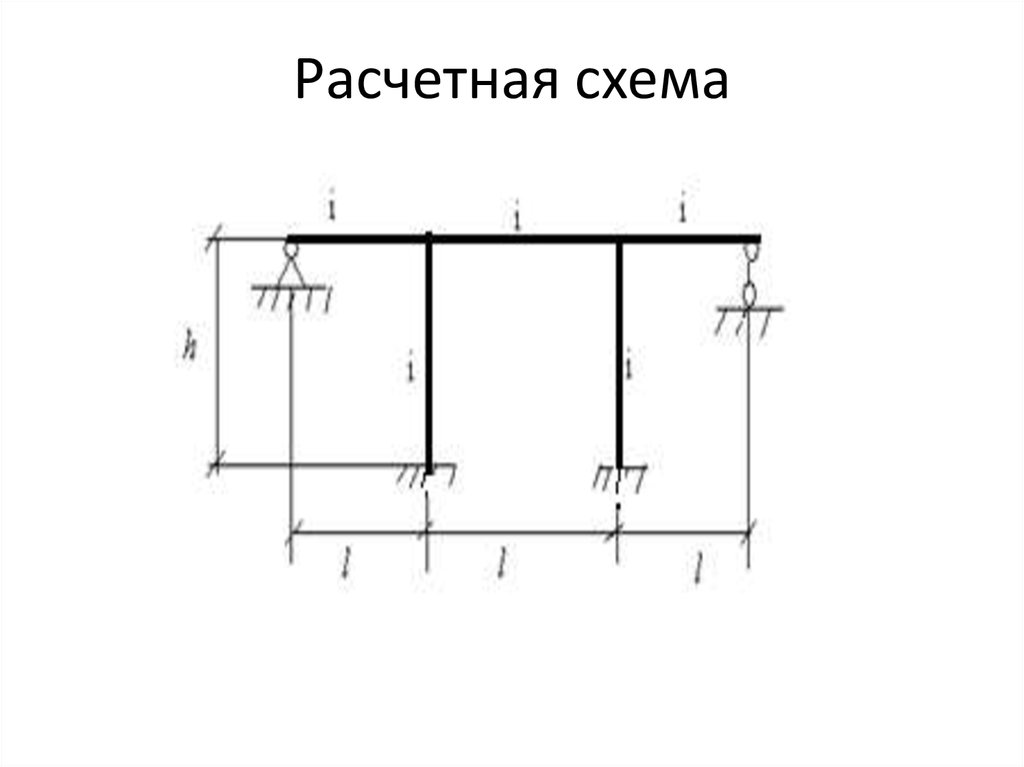
Пример 1
Определить собственные частоты поперечных
колебаний симметричной рамы с распределенной
массой по длине стержней (рисунок 1). Пусть
высота стоек и длины пролетов одинаковы, а
интенсивность распределения масс постоянная
величина, т.е.
h= l 6 м, m const

2. Расчетная схема

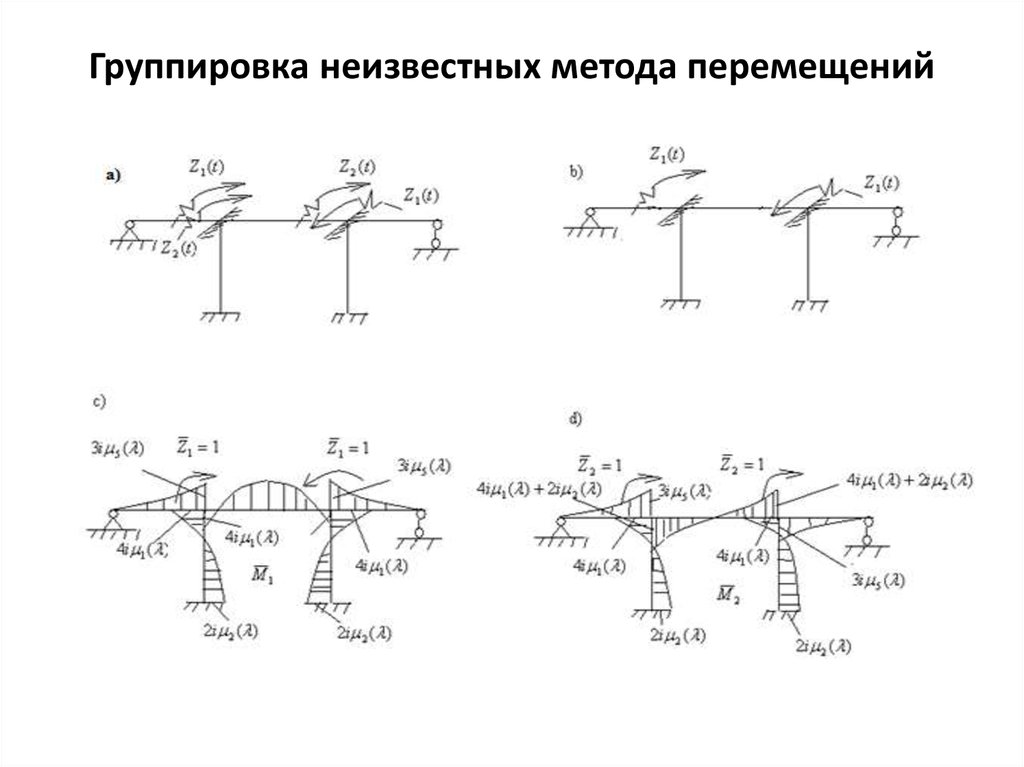
3. Группировка неизвестных метода перемещений

4. Канонические уравнения

Z1 (t ) Z1 Sin t,
r11 Z 1 R1 p 0,
r11 0,
Z 2 (t ) Z 2 Sin t
r22 Z 2 R2 p 0
r22 0
2
m
l4
EI
r11 2 3i 5 ( ) 4i 1 ( ) 4i 1 ( ) 2i 2 ( ) 0,
r22 2 3i 5 ( ) 4i 1 ( ) 4i 1 ( ) 2i 2 ( ) 0
r11 3i 5 ( ) 8i 1 ( ) 2i 2 ( ) 0,
r22 3i 5 ( ) 8i 1 ( ) 2i 2 ( ) 0
2
i
2 EI
(
)
3
l
m
ml

5.

Подставляя заданные значения длин пролетов,
получаем следующие значения для симметричных
частот собственных колебаний:
λ 1=3,34;
EI
1 0,318
,
m
λ2=4,25;
λ3=4,73
EI
2 0,501
,
m
EI
1 0,622
m
Для обратносимметричных форм собственных
колебаний получаем:
λ 1=3,6;
EI
1 0,36
,
m
λ2=4,53
EI
2 0,57
,
m
λ3=5,02
EI
1 0,68
m

6.

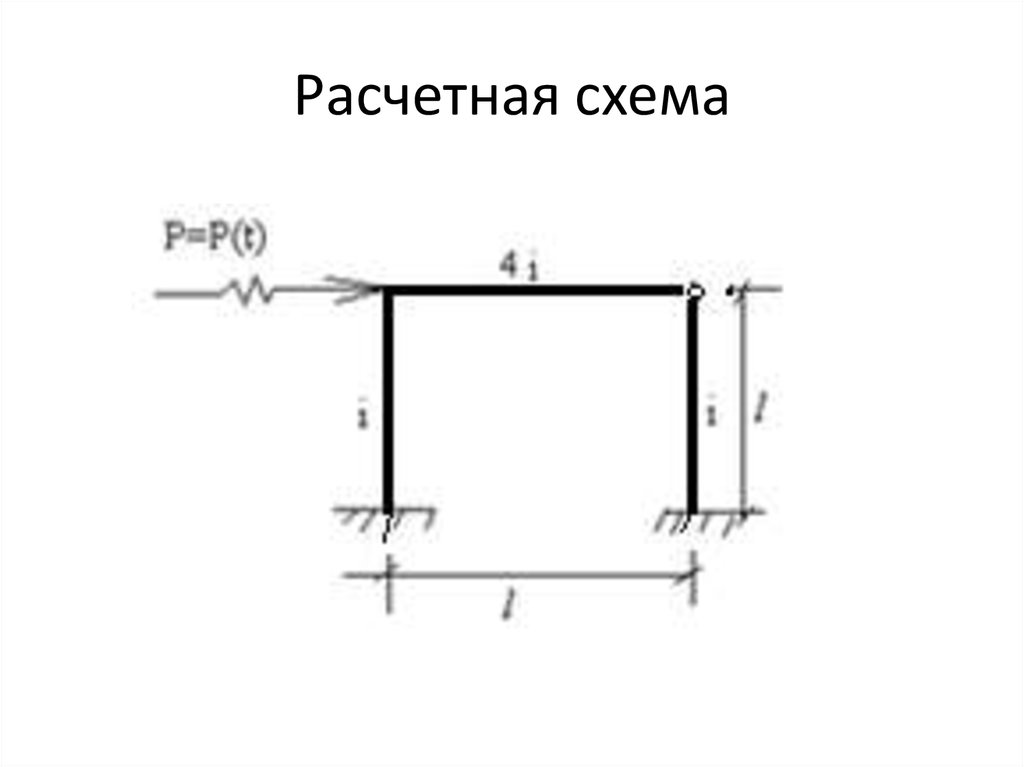
Пример 2
Построить эпюру динамических изгибающих
моментов в раме с распределенной массой по
длине стержней, показанной на рисунке 3,а от
действия возмущающей силы P(t)=P Sinθt, где θчастота внешней силы. Пусть θ =0,8ω, где ωсобственная частота основного тона колебаний.
Погонные массы ригеля и стоек постоянны, т.е.
m=const.

7. Расчетная схема

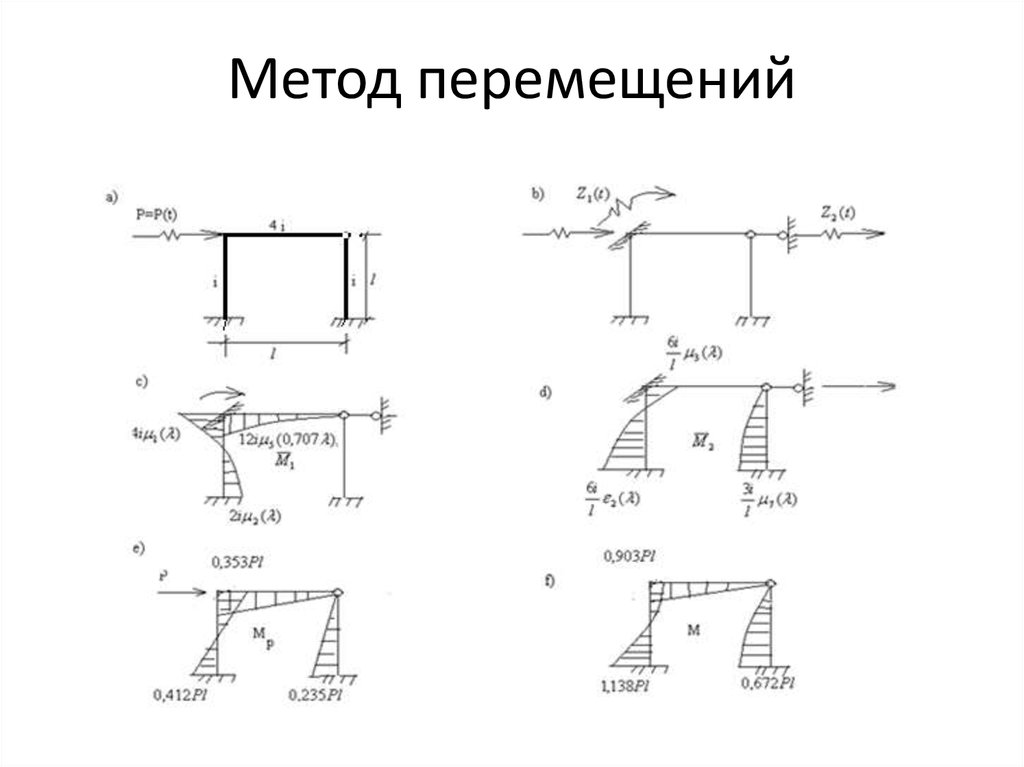
8. Метод перемещений

9. Определение собственных частот

Z1 (t ) Z1 Sin t,
Z 2 (t ) Z 2 Sin t
r11Z1 r12 Z 2 R1 p 0,
r21Z1 r22 Z 2 R2 p 0
r11 4i 1 ( ) 12i 5 (0,707 ) ,
6i
r12 r21 3 ( ) ,
l
3i
i 4
12i
r22 2 3 ( ) 2 8 ( ) 2 0, R1 p 0, R2 p P
l
l
l
D
r11
r12
r21
r22
0,
r11r22 r122 0
1 ( )
l
2
EI 2,82 EI
2
m
m
l

10. Динамический расчет

2,25 EI
По условию θ=0,6ω1= l 2 m ,
следовательно, λ=√2,25=1,5.
2
m
l4
EI
Подставив специальные функции в канонические уравнения , после их
решения, находим:
Z1=0,0759Pl/i, Z2=0,210Pl2/i. Окончательная эпюра
динамических изгибающих моментов на основе принципа независимости
действия сил, определяется по следующей формуле:
M MZ1 MZ 2 M p
Окончательная эпюра амплитудных значений изгибающих моментов представлена
на рисунке (3,f). На рисунке (3е) показана эпюра изгибающих моментов от
статической нагрузки, равной амплитудному значению силы P(t). Наибольший
динамический коэффициент по изгибающим моментам равен:
μmax =
1,138
2,76
0,412