Пример динамического расчета плоской рамы с сосредоточенными массами при действии гармонических нагрузок

1. Лекция 13-14

Содержание
1 Пример динамического расчета плоской
рамы с сосредоточенными массами при
действии гармонических нагрузок

2. Расчетная схема рамы

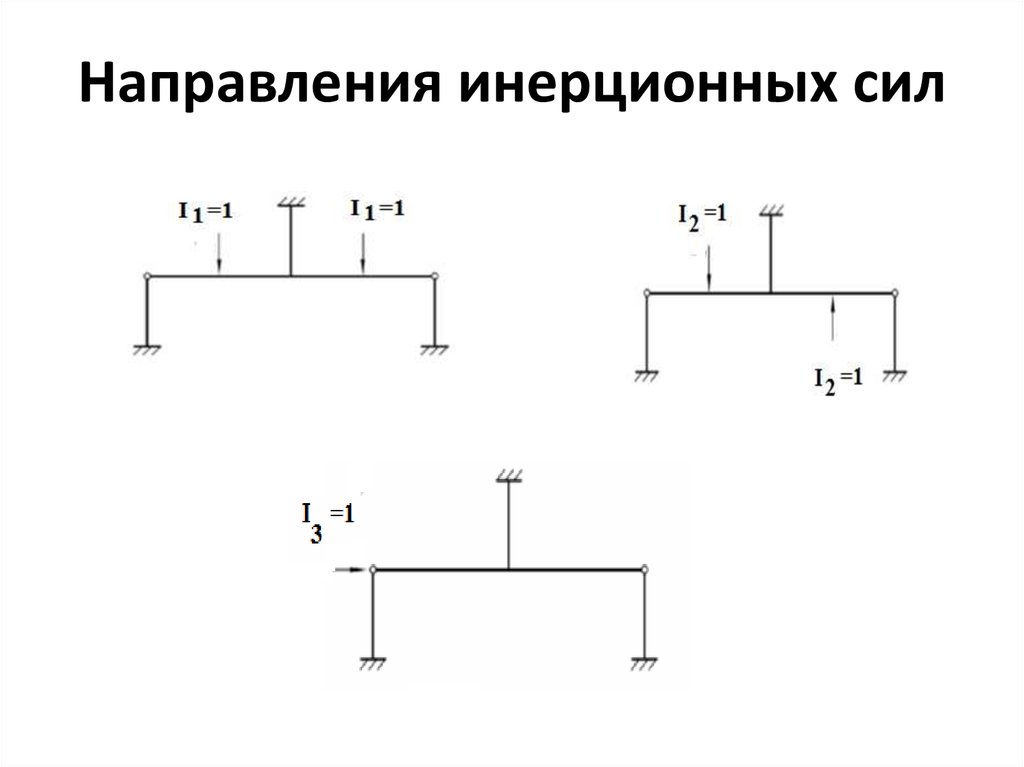
3. Направления инерционных сил

4. Амплитудные значения инерционных сил

min 2
EI
9,674 m
0,7 min 0,7
EI
EI
9,674 m
19,74 m
*
I1 11
I 2 12 I 3 13 1p 0;
*
I1 21 I 2 22 I 3 23 2 p 0;
*
I1 31 I 2 32 I 3 33 3p 0.

5.

*
ii
ii
1
m 2
;
M12 dx
14
11
.
EI
3EI
M 32 dx 40
33
;
EI
9EI
M3 M 2dx 2
32 23
;
EI
EI
M 22dx 55
22
;
EI
6EI
*33
*
11
14
19,74 m
34,32
.
3EI 0,5m EI
EI
40 19,74 m
5,43
55
19,74 m
30,32
*
; 22
;
9EI 2m EI
EI
6EI 0,5m EI
EI

6. Метод перемещений для построения грузовой эпюры

7.

Грузовые
коэффициенты
в
канонических
уравнениях метода перемещений равны:
R1p=qL2/8=160,
R2p=-P=-30
Канонические уравнения имеют вид:
5EI
6EI
Z1
Z2
160 0
2
16
6EI
18EI
Z1
Z2
30 0,
16
64
Z1 100,
Z2 240

8. Эпюра изгибающих моментов в заданной раме от амплитудных значений вибрационной нагрузки

M р M1Z1 M 2 Z2 M 0 p M1 ( 100) M 2 240 M 0 p ,

9. Определение коэффициентов (грузовые коэффициенты)

1p
M1 M p dx
EI
1 4
5
5 4
5
1
4 98,8 117 ,5
117 ,5 4 117 ,5
EI 2 6
8
4 2 6
4
8
3 4
3
5
3
5
1 1 5 2
85
2 75 2 37,5 37,5 37,5 4 37,5
2 2 6
2
4
2
4
2 2 4 3
213,3
.
EI

10.

3p
M 3 M p dx
EI
1 1 5
2 5
8
1
1 1 1 1
2 4 45
4 117 ,5 85 8
EI 2 6
3 6
2 6
4
2 2 2 2
2
4
1
1
240
75 2 1 10 2 40 10 40 1
;
3
6
3
3
EI
2
4
29
29
1 3
2 4 45
4 98,8
117 ,5
2
8
3
2
6
32
16
4
29
11,5
3 4
3
3
117 ,5
4 56,3
85 2 10 40
2 6
16
16
8 6
4
4
2p M 2 M p
1
EI
4
3
29
3
29
1 29 2
512,4
2 75 2 37,5 37,5 75 2
4 37,5
;
2 6
8
16
8
16
2 16 3
EI

11. Уравнения для амплитудных значений инерционных сил

34,32
213,3
0 I1 0 I 2 EI I 3 EI 0.
30,32
512 ,4
2
I 2 0 I3
0;
I1
EI
EI
EI
2
240
5,43
EI I1 EI I 2 0 I 3 EI 0;

12. Амплитудные значения инерционных сил

I3 = 51,6 кН; I2 = 20,3 кН; I1 = 6,2 кН
M дин M1I1 M 2 I 2 M 3I3 M p M1 (6,2) M 2 (20,3) M 3 (51,6) M p ,

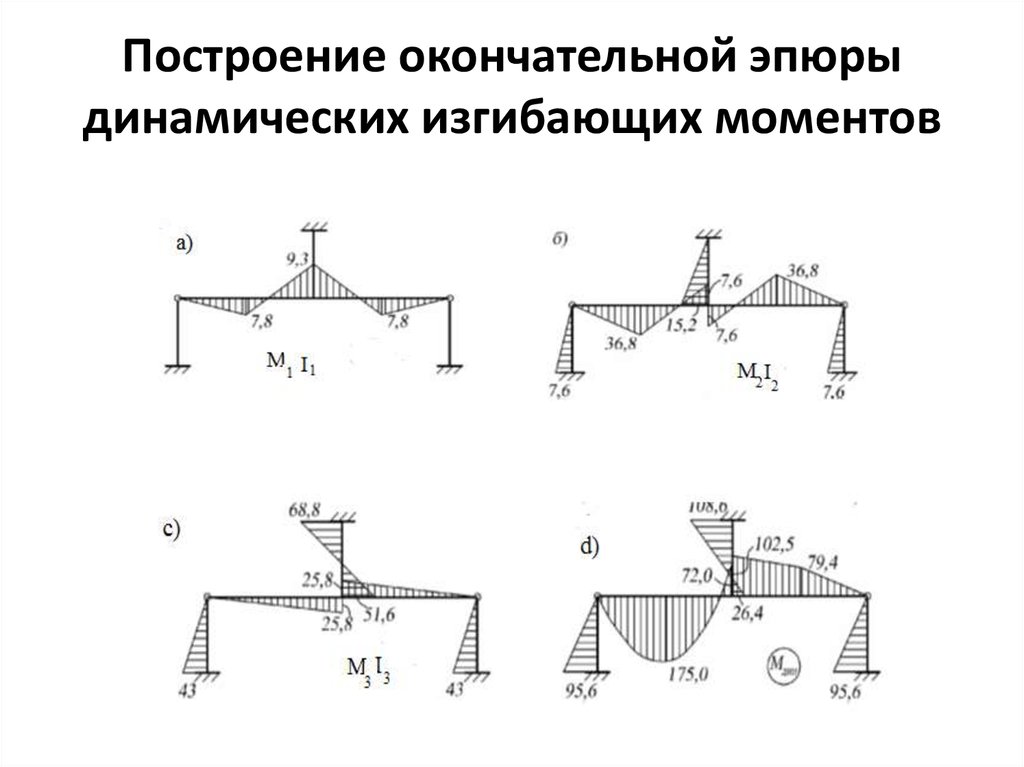
13. Построение окончательной эпюры динамических изгибающих моментов

14. Динамический коэффициент

M дин мах
М ст
175
1,49
117 ,5