Теория пар и моментов. Тема 2

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
Кафедра строительной механики
Теоретическая механика
Тема 1
Статика. Момент силы относительно
точки и оси. Пара сил, теоремы о парах.
Юлина Анна Олеговна
1

2.

Лекция № 2
Тема 2. Теория пар и моментов
УЧЕБНЫЕ ВОПРОСЫ
1. Момент силы относительно точки и оси.
2. Пара сил. Момент пары.
3. Теоремы о парах.
4. Уравнения равновесия системы пар.

3.

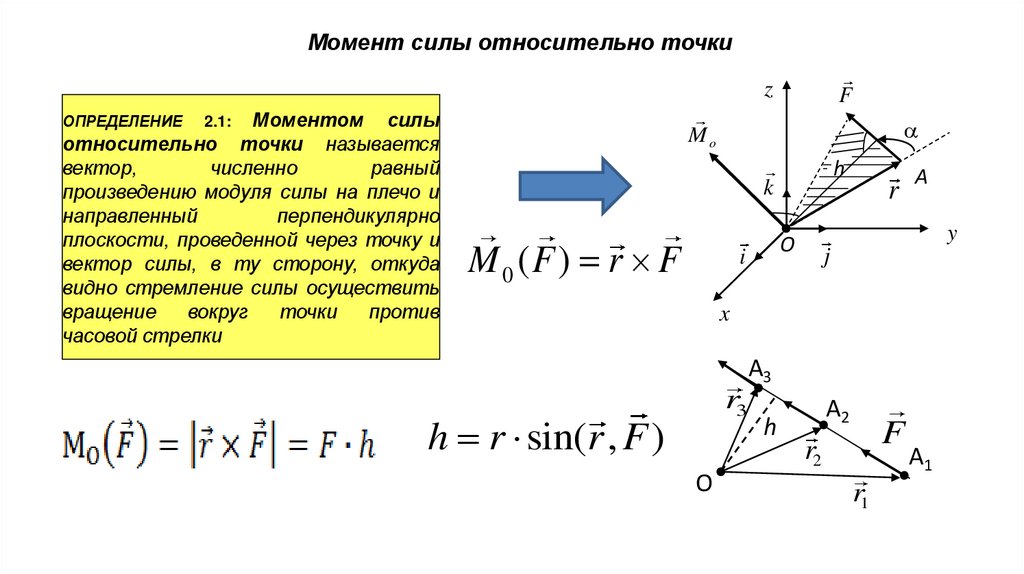
Момент силы относительно точки
z
Моментом силы
относительно точки называется
вектор,
численно
равный
произведению модуля силы на плечо и
направленный
перпендикулярно
плоскости, проведенной через точку и
вектор силы, в ту сторону, откуда
видно стремление силы осуществить
вращение
вокруг
точки
против
часовой стрелки
ОПРЕДЕЛЕНИЕ
2.1:
F
Mo
h
k
M 0 (F ) r F
A
y
O
i
r
j
x
А3
r3
h r sin(r , F )
О
h
А2
F
r2
r1
А1

4.

Момент силы относительно оси
Моментом силы относительно оси называется проекция вектора момента силы
относительно точки на ось, проходящую через эту точку.
M x ( F ) yFz zFy ;
M y ( F ) zFx xFz ;
M z ( F ) xFy yFx

5.

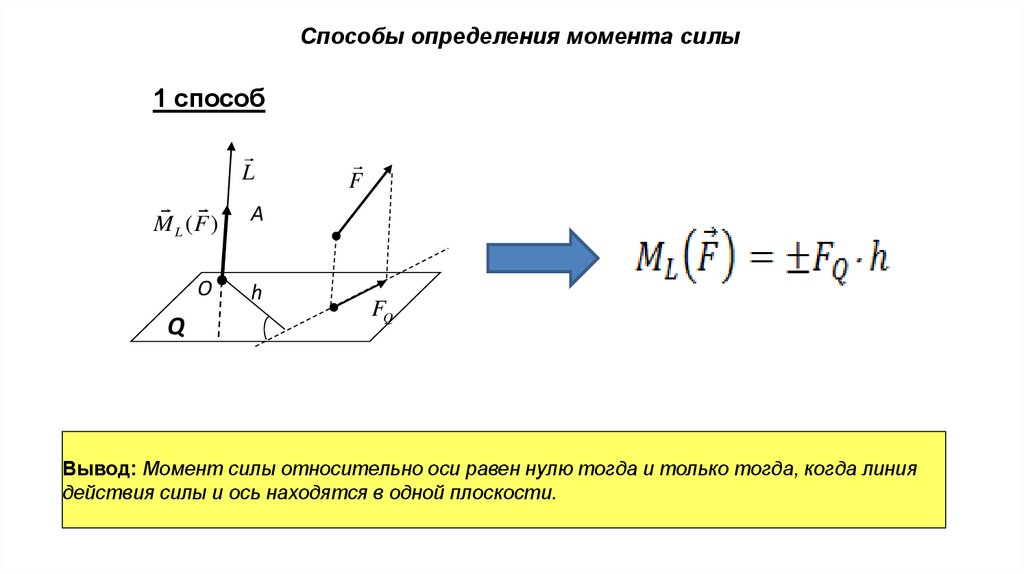
Способы определения момента силы
1 способ
L
M L (F )
O
Q
F
A
h
FQ
Вывод: Момент силы относительно оси равен нулю тогда и только тогда, когда линия
действия силы и ось находятся в одной плоскости.

6.

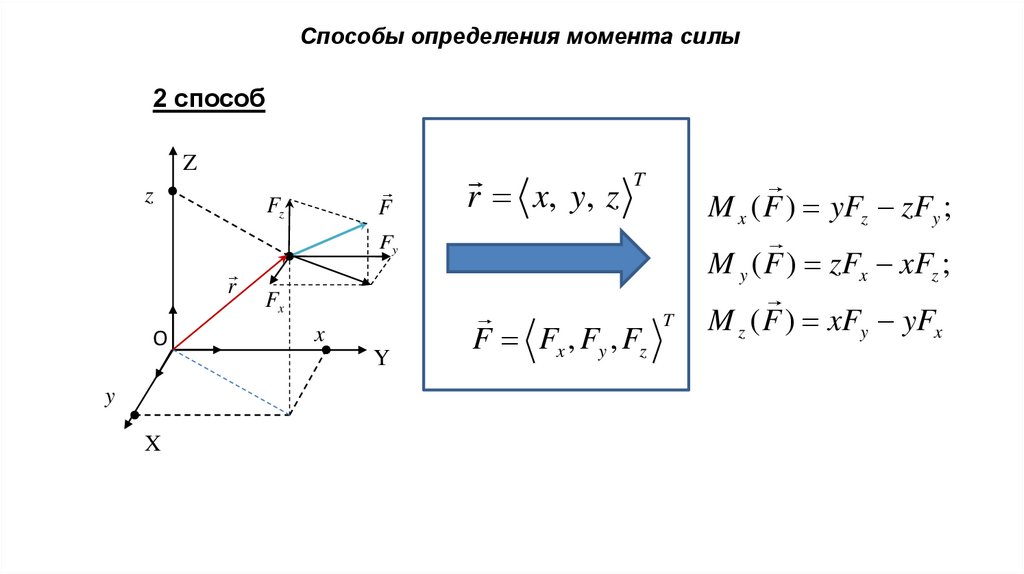
Способы определения момента силы
2 способ
Z
z
Fz
F
r x, y , z
T
M x ( F ) yFz zFy ;
Fy
r
O
y
X
M y ( F ) zFx xFz ;
Fx
x
Y
F Fx , Fy , Fz
T
M z ( F ) xFy yFx

7.

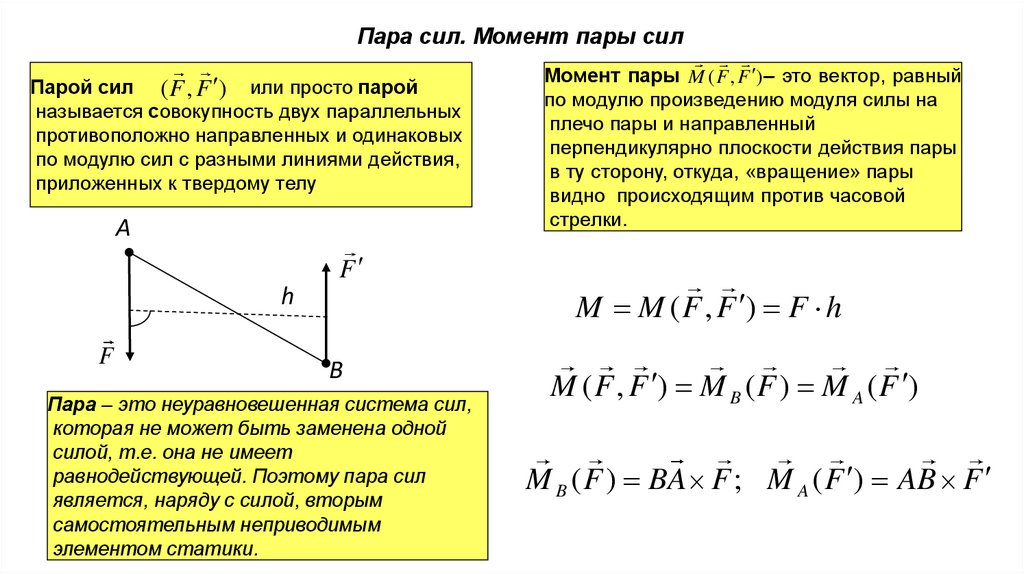
Пара сил. Момент пары сил
Парой сил ( F , F ) или просто парой
называется совокупность двух параллельных
противоположно направленных и одинаковых
по модулю сил с разными линиями действия,
приложенных к твердому телу
А
Момент пары M ( F , F ) – это вектор, равный
по модулю произведению модуля силы на
плечо пары и направленный
перпендикулярно плоскости действия пары
в ту сторону, откуда, «вращение» пары
видно происходящим против часовой
стрелки.
F
M M ( F , F ) F h
h
F
B
Пара – это неуравновешенная система сил,
которая не может быть заменена одной
силой, т.е. она не имеет
равнодействующей. Поэтому пара сил
является, наряду с силой, вторым
самостоятельным неприводимым
элементом статики.
M ( F , F ) M B ( F ) M A ( F )
M B ( F ) BA F ; M A ( F ) AB F

8.

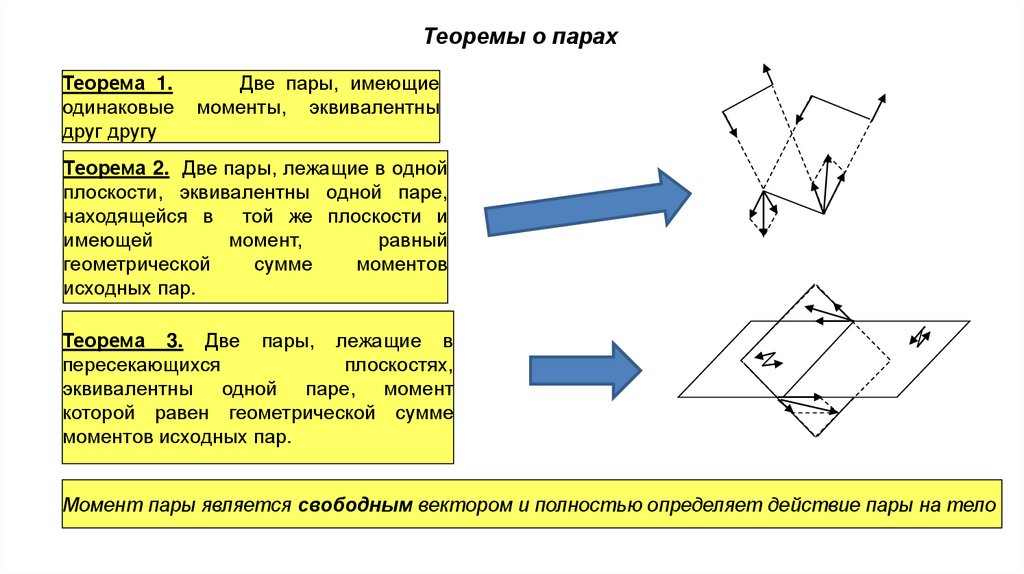
Теоремы о парах
Теорема 1.
одинаковые
друг другу
Две пары, имеющие
моменты, эквивалентны
Теорема 2. Две пары, лежащие в одной
плоскости, эквивалентны одной паре,
находящейся в той же плоскости и
имеющей
момент,
равный
геометрической
сумме
моментов
исходных пар.
Теорема 3. Две пары, лежащие в
пересекающихся
плоскостях,
эквивалентны одной паре, момент
которой равен геометрической сумме
моментов исходных пар.
Момент пары является свободным вектором и полностью определяет действие пары на тело

9.

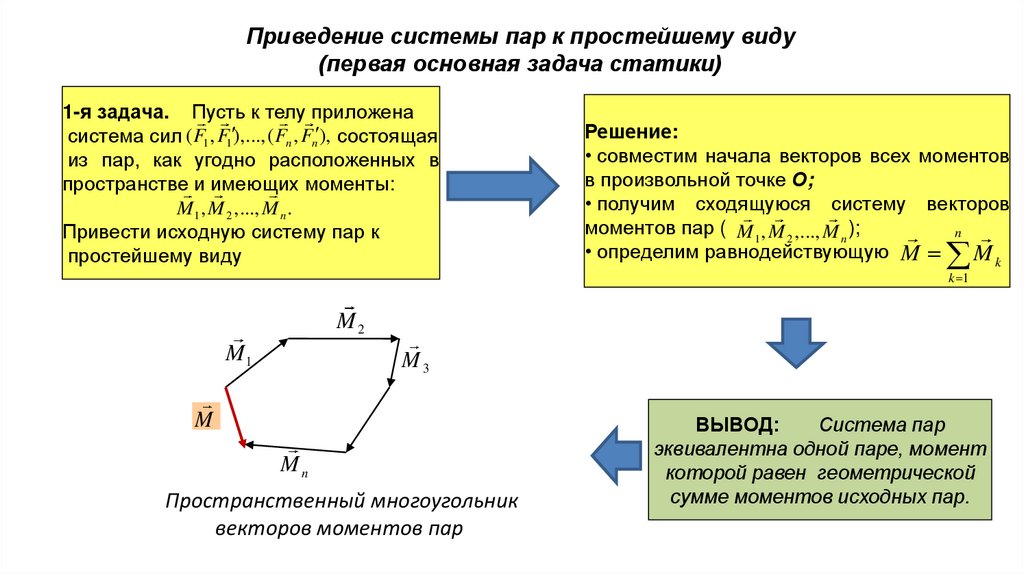
Приведение системы пар к простейшему виду
(первая основная задача статики)
1-я задача. Пусть к телу приложена
система сил ( F1 , F1 ),...,( Fn , Fn ), состоящая
из пар, как угодно расположенных в
пространстве и имеющих моменты:
M 1 , M 2 ,..., M n .
Привести исходную систему пар к
простейшему виду
Решение:
• совместим начала векторов всех моментов
в произвольной точке О;
• получим сходящуюся систему векторов
моментов пар ( M 1 , M 2 ,..., M n );
n
• определим равнодействующую M
Mk
k 1
M2
M1
M3
M
Mn
Пространственный многоугольник
векторов моментов пар
ВЫВОД:
Система пар
эквивалентна одной паре, момент
которой равен геометрической
сумме моментов исходных пар.

10.

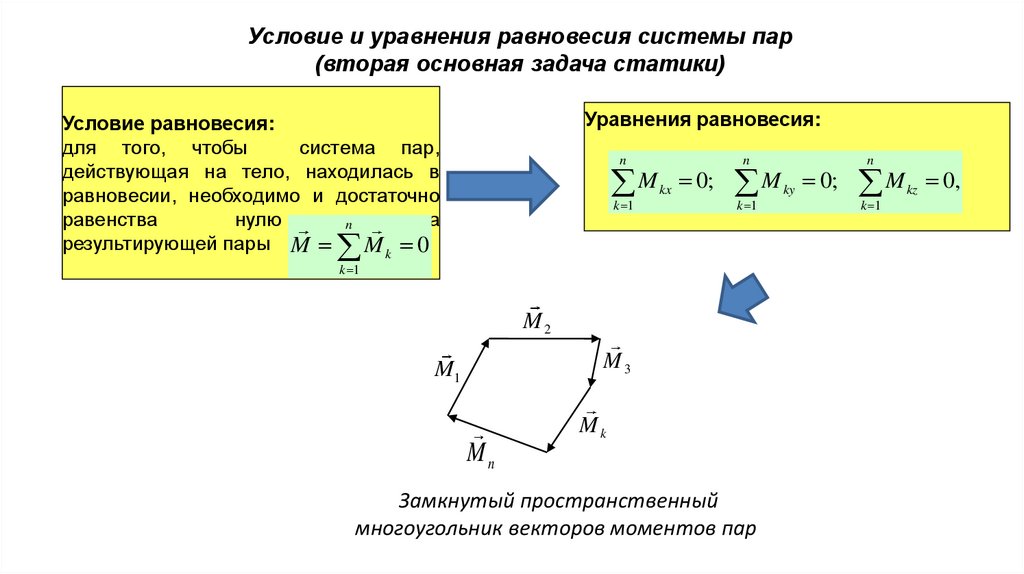
Условие и уравнения равновесия системы пар
(вторая основная задача статики)
Уравнения равновесия:
Условие равновесия:
для того, чтобы
система пар,
действующая на тело, находилась в
равновесии, необходимо и достаточно
равенства
нулю
n момента
результирующей пары M
Mk 0
n
n
n
M 0; M 0; M 0,
k 1
kx
k 1
k 1
M2
M3
M1
Mk
Mn
Замкнутый пространственный
многоугольник векторов моментов пар
ky
k 1
kz

11.

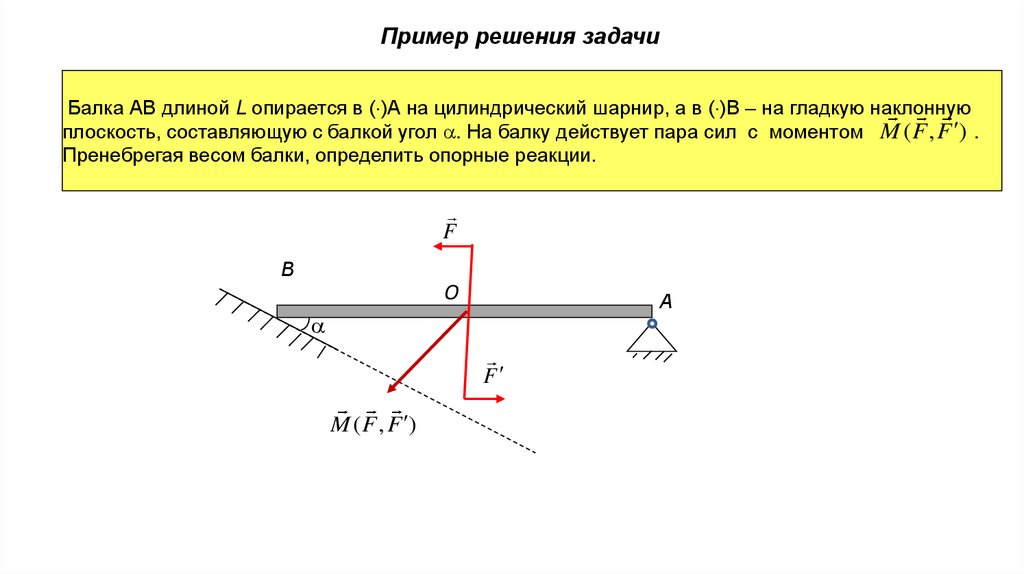
Пример решения задачи
Балка АВ длиной L опирается в ( )А на цилиндрический шарнир, а в ( )В – на гладкую наклонную
плоскость, составляющую с балкой угол . На балку действует пара сил с моментом M ( F , F ) .
Пренебрегая весом балки, определить опорные реакции.
F
В
О
А
F
M ( F , F )

12.

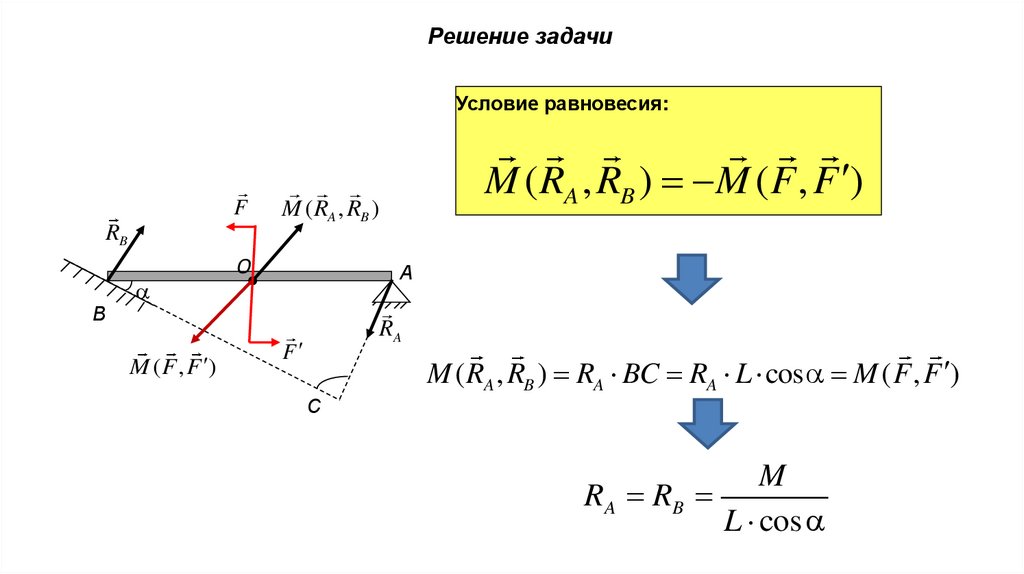
Решение задачи
Условие равновесия:
F
RB
В
M ( F , F )
M ( RA , RB ) M ( F , F )
M ( RA , RB )
О
А
RA
F
M ( RA , RB ) RA BC RA L cos M ( F , F )
С
RA RB
M
L cos