Теорема о трех силах. (Лекция 2)

1.

ТЕОРЕМА
ТЕОРЕМА О
О ТРЕХ
ТРЕХ СИЛАХ
СИЛАХ
Если твердое тело находится в равновесии
под действием трех непараллельных сил,
лежащих в одной плоскости, то линии
действия этих сил пересекаются в одной
точке.

2.

ТЕОРЕМА
ТЕОРЕМА О
О ТРЕХ
ТРЕХ СИЛАХ
СИЛАХ
Вес диска
G 250 2 H ;
А
G
реакция шарнира RA=… H.

3.

ТЕОРЕМА
ТЕОРЕМА О
О ТРЕХ
ТРЕХ СИЛАХ
СИЛАХ
Решение:
RA
RA
G
G
R
R

4.

МОМЕНТ
МОМЕНТ СИЛЫ
СИЛЫ ОТНОСИТЕЛЬНО
ОТНОСИТЕЛЬНО ТОЧКИ
ТОЧКИ
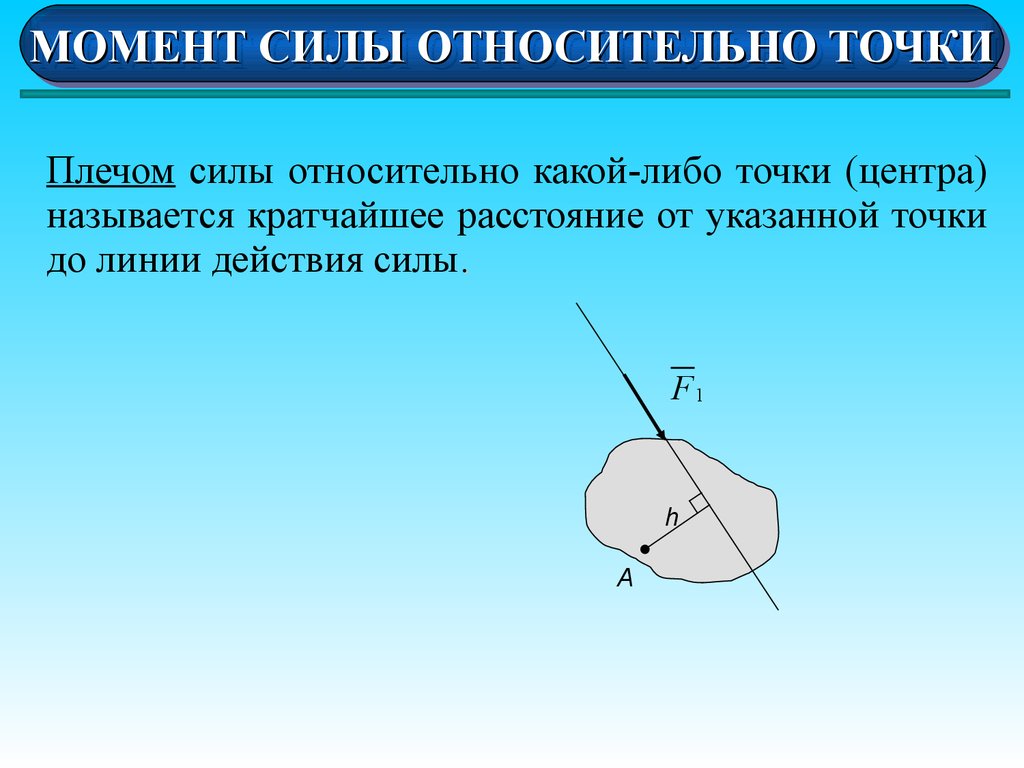
Плечом силы относительно какой-либо точки (центра)
называется кратчайшее расстояние от указанной точки
до линии действия силы.
F1
h
A

5. Момент силы относительно центра это вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, п

МОМЕНТ
МОМЕНТ СИЛЫ
СИЛЫ ОТНОСИТЕЛЬНО
ОТНОСИТЕЛЬНО ТОЧКИ
ТОЧКИ
Момент силы относительно центра это вектор, численно
равный произведению модуля силы на плечо и направленный
перпендикулярно плоскости, проходящей через выбранную
точку и вектор силы, в ту сторону, откуда “вращение” силы
вокруг точки направлено против хода часовой стрелки.
M0 ( F ) r ´ F
M 0 F × r × sin F × h
B
F
h
MO(F)
O
r
A

6.

МОМЕНТ
МОМЕНТ СИЛЫ
СИЛЫ ОТНОСИТЕЛЬНО
ОТНОСИТЕЛЬНО ТОЧКИ
ТОЧКИ
Алгебраический момент силы
Алгебраический момент силы F относительно центра
О
равен взятому с соответствующим знаком
произведению модуля силы на ее плечо
M O ( F ) Fh
Правило знаков: момент считается положительным,
когда сила стремится повернуть тело вокруг центра О
по ходу часовой стрелки

7.

ПАРА
ПАРА СИЛ
СИЛ
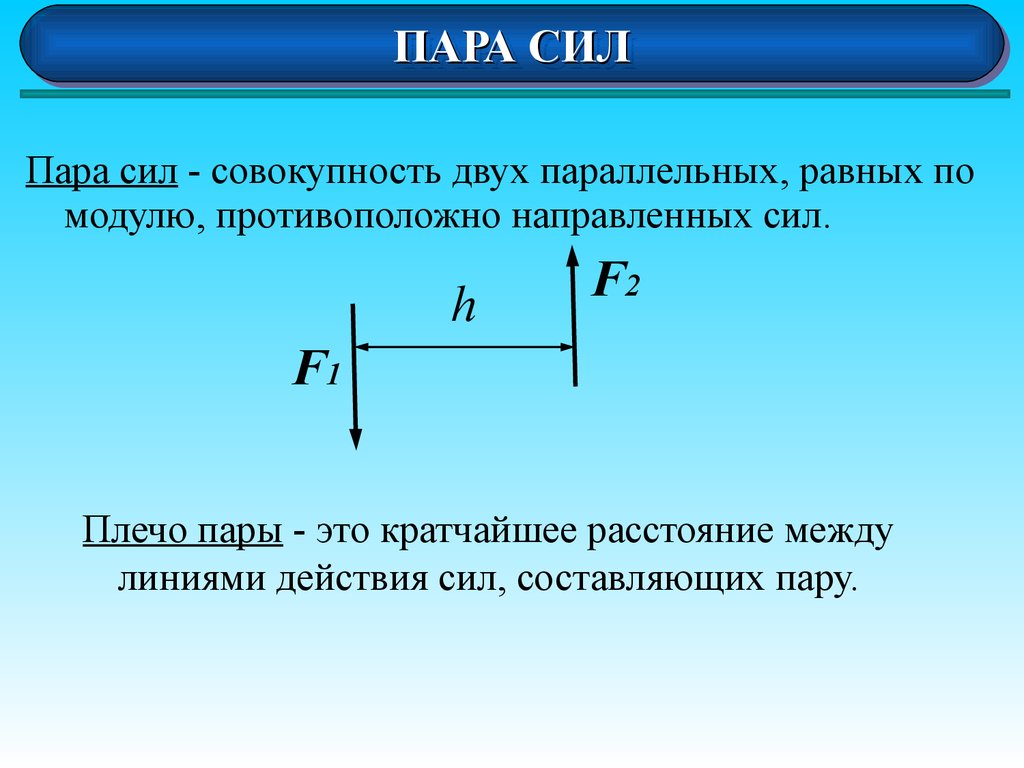
Пара сил - совокупность двух параллельных, равных по
модулю, противоположно направленных сил.
h
F2
F1
Плечо пары - это кратчайшее расстояние между
линиями действия сил, составляющих пару.

8.

ПАРА
ПАРА СИЛ
СИЛ
Момент пары сил - это вектор, численно равный
произведению модуля силы на плечо пары; направлен
перпендикулярно плоскости, в которой лежит пара, в ту
сторону, откуда поворот пары виден происходящим
против хода часовой стрелки.
F
A
А
F
M
h
К
'
'
M ( F , F ' )× A,' A F
Оказалось, что момент пары не
зависит
от
выбора
центра О.
Алгебраический
момент
пары
равен:
M F × h

9.

ПАРА
ПАРА СИЛ
СИЛ
На плоскости пара сил изображается
m
А
В
М
Свойства пар
1. Момент пары – свободный вектор, т.е. пару можно
переносить в плоскости ее действия и в параллельную
плоскость.

10.

ПАРА
ПАРА СИЛ
СИЛ
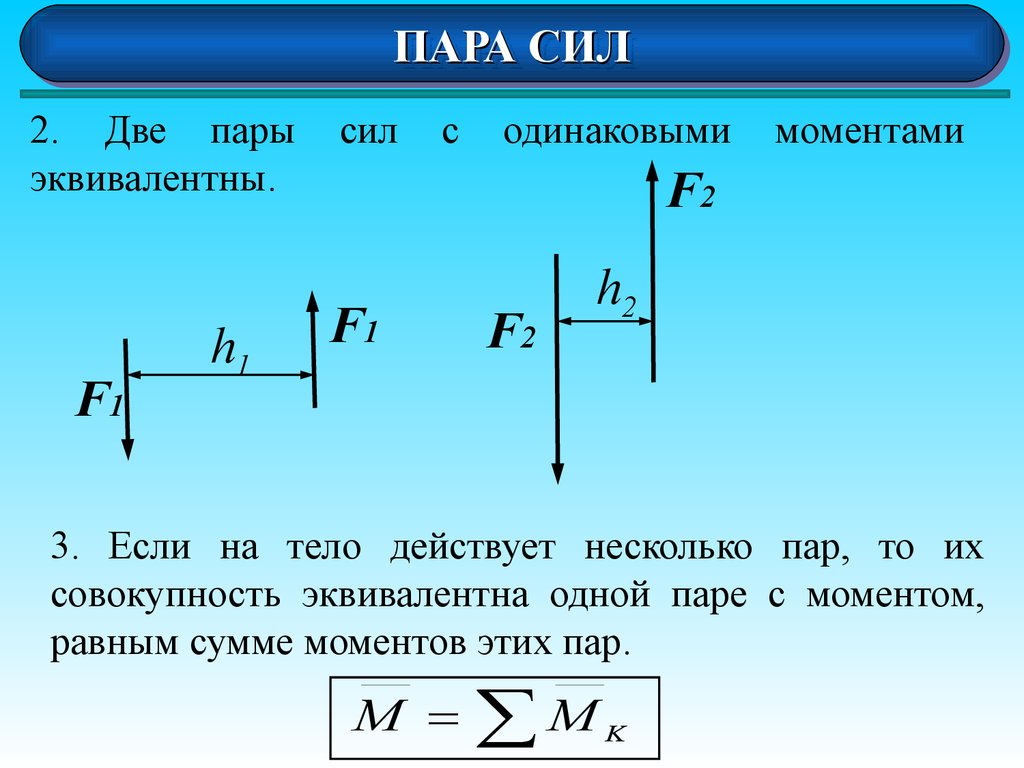
2. Две пары
эквивалентны.
F1
h1
сил
с
одинаковыми
моментами
F2
F1
F2
h2
3. Если на тело действует несколько пар, то их
совокупность эквивалентна одной паре с моментом,
равным сумме моментов этих пар.
M
M
K

11.

ТЕОРЕМА
ТЕОРЕМА О
О ПАРАЛЛЕЛЬНОМ
ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ
ПЕРЕНОСЕ СИЛЫ
СИЛЫ
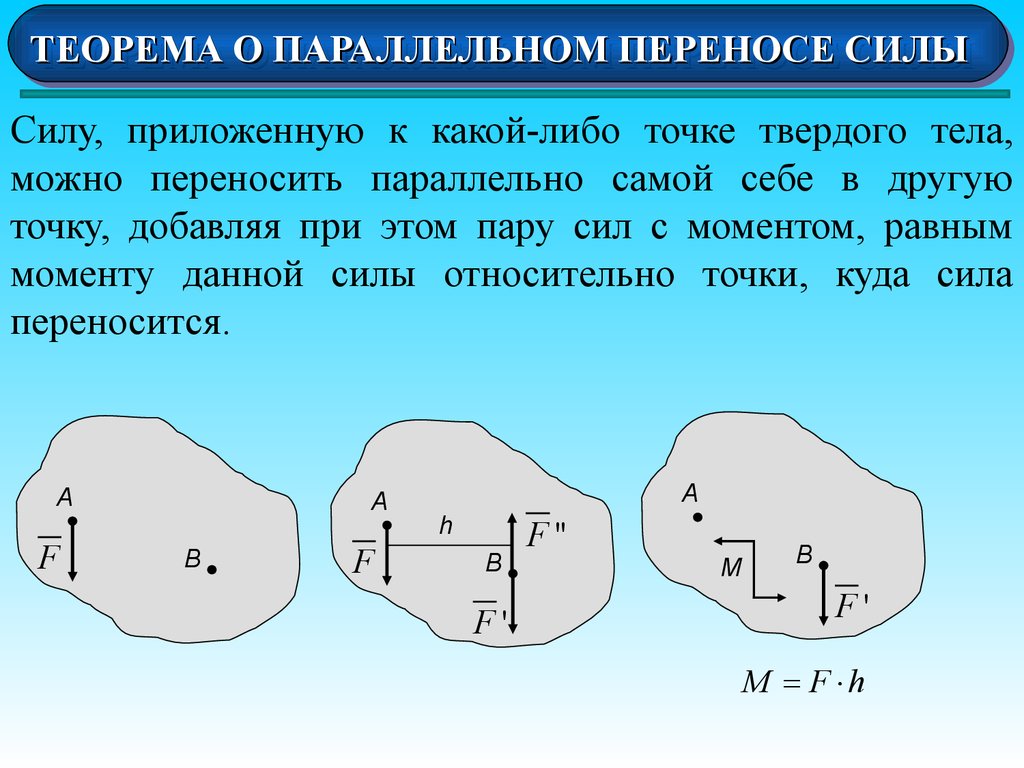
Силу, приложенную к какой-либо точке твердого тела,
можно переносить параллельно самой себе в другую
точку, добавляя при этом пару сил с моментом, равным
моменту данной силы относительно точки, куда сила
переносится.
А
F
А
В
F
А
h
В
F'
F"
M
В
F'
M F ×h

12.

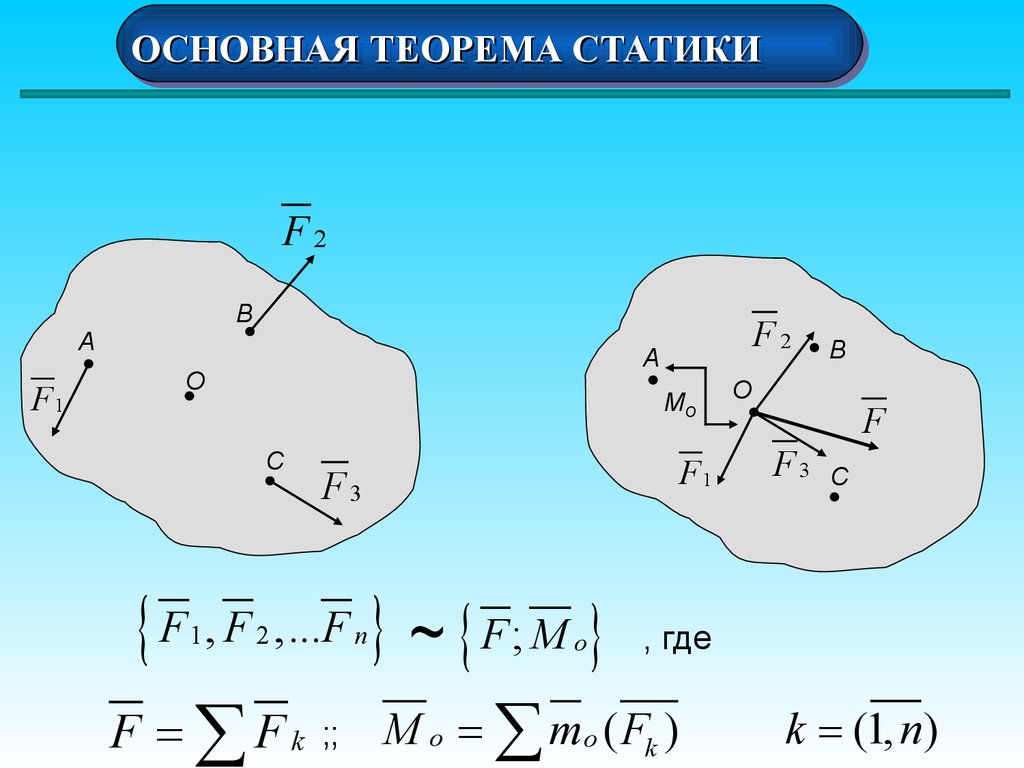
ОСНОВНАЯ
ОСНОВНАЯ ТЕОРЕМА
ТЕОРЕМА СТАТИКИ
СТАТИКИ
Главным вектором системы сил называется
геометрическая сумма всех сил системы
R FK
Главным моментом системы сил относительно центра О
называется геометрическая сумма моментов всех сил
относительно этого центра
MO
M
O
( FK )

13.

ОСНОВНАЯ
ОСНОВНАЯ ТЕОРЕМА
ТЕОРЕМА СТАТИКИ
СТАТИКИ
Теорема Пуансо
Всякую пространственную систему сил можно
заменить эквивалентной системой, состоящей из силы,
приложенной в выбранном центре и равной главному
вектору, и пары сил, момент которой равен главному
моменту всех сил относительно выбранного центра.

14.

ОСНОВНАЯ
ОСНОВНАЯ ТЕОРЕМА
ТЕОРЕМА СТАТИКИ
СТАТИКИ
F2
В
А
F1
F2
А
O
MO
C
F1
F3
{ F , F ,...F } ~ { F ; M } , где
F F ;; M m ( F )
1
2
n
k
В
O
F
F
F3
C
o
o
o
k
k (1, n)

15.

УСЛОВИЯ
УСЛОВИЯ РАВНОВЕСИЯ
РАВНОВЕСИЯ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Для равновесия любой системы сил необходимо и
достаточно, чтобы главный вектор этой системы сил и ее
главный момент относительно любого центра были
равны нулю
F
k
0,
M ( F ) 0.
O
k

16. Первая (основная) форма уравнений равновесия:

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Плоской называется система сил, как угодно
расположенных в одной плоскости.
Первая (основная) форма уравнений равновесия:
1. Fkx 0 ,
2. Fky 0 ,
3. M O ( Fk ) 0 .
Для
равновесия
плоской
системы
сил
необходимо и достаточно, чтобы алгебраические
суммы проекций всех сил на две координатные оси и
алгебраическая сумма моментов всех сил относительно
произвольной точки равнялись нулю.

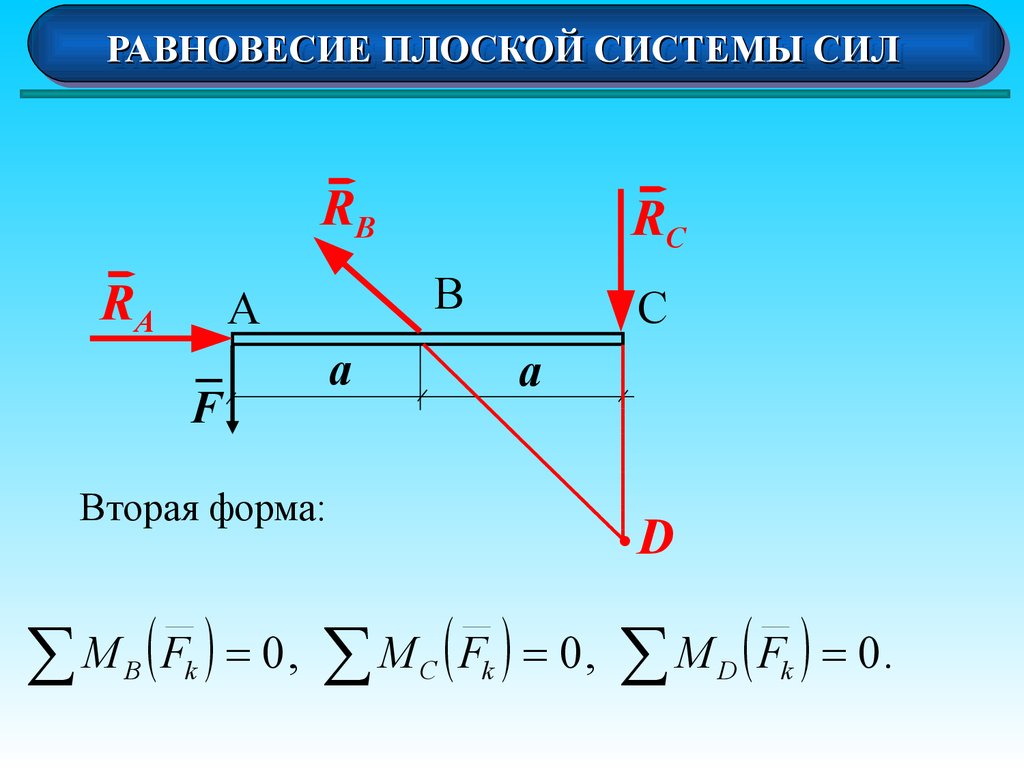
17. Вторая форма:

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Вторая форма:
M ( F ) 0,
M ( F ) 0,
M ( F ) 0,
A
k
B
k
C
k
Для равновесия плоской системы сил необходимо
и достаточно, чтобы суммы моментов всех сил
относительно любых трех точек, не лежащих на одной
прямой, были равны нулю.

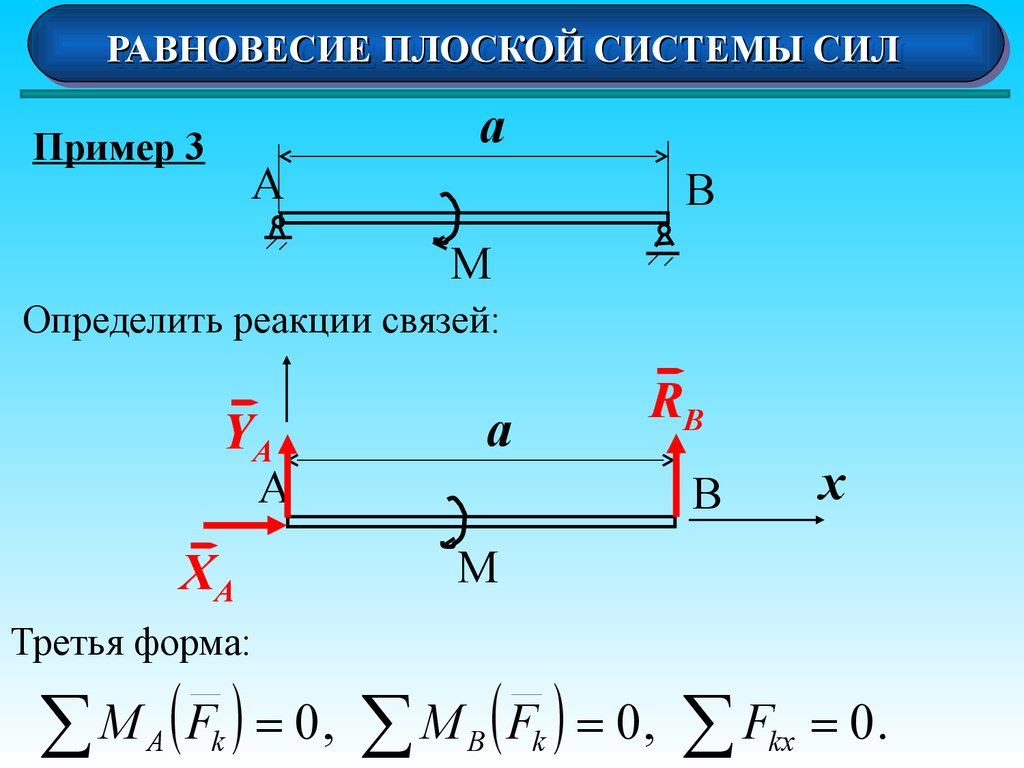
18. Третья форма:

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Третья форма:
M ( F ) 0,
M ( F ) 0,
F 0.
A
k
B
k
kx
Для
равновесия
плоской
системы
сил
необходимо и достаточно, чтобы суммы моментов всех
сил относительно любых двух точек А и В и сумма
проекций сил на ось Оx, не перпендикулярную прямой
АВ, были равны нулю.

19. Пример 1

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Пример 1
l
A
F
Определить реакции связи.

20.

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
y
YA
XA
MA
A
x
F
X A F × cos 0 , X A F × cos .
YA F × sin 0, YA F × sin .
M A F × sin × l 0
M A F × l × sin .

21. Пример 2

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
Пример 2
А
F
45
В
а
С
а

22.

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
RB
RA
В
А
F
RC
С
а
а
.D
Вторая форма:
M ( F ) 0 , M ( F ) 0 , M ( F ) 0.
B
k
C
k
D
k

23.

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
F × a RC × a 0 , RC F .
F × 2a RB × a × sin 45 0 ,
o
RB 2 F sin 45 ; RB 2 2 × F .
o
F × 2a RA × a 0 ,
RA 2 F .

24. Пример 3

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
а
Пример 3
А
В
М
Определить реакции связей:
RB
а
YA
А
XA
x
В
М
Третья форма:
M ( F ) 0, M ( F ) 0, F
A
k
B
k
kx
0.

25.

РАВНОВЕСИЕ
РАВНОВЕСИЕ ПЛОСКОЙ
ПЛОСКОЙ СИСТЕМЫ
СИСТЕМЫ СИЛ
СИЛ
RB × a M 0 ,
YA × a M 0 ,
M
RB
.
a
M
YA
.
a
X A 0.