Similar presentations:
Система параллельных сил. Лекция 3
1. Новосибирский Государственный Архитектурно- Строительный Университет (Сибстрин)
Новосибирский Государственный АрхитектурноСтроительный Университет (Сибстрин)Лекция 3.
Система параллельных сил.
Теория пар сил
Из того, что пересекающиеся силы имеют
равнодействующую, следует, что
параллельные имеют ее тоже, поскольку
последние являются частным случаем
пересекающихся.
Николай Егорович Жуковский
Кафедра теоретической механики
2.
Николай Егорович Жуковский1847-1921, Москва
2
3. На предыдущей лекции
• Изучили систему сходящихся сил• Показали, что ССС имеет
равнодействующую
• Установили уравнения равновесия
ССС
• Познакомились с алгоритмом
решения задач статики
• Ввели понятие момента силы
относительно точки и оси
3
4. Цель лекции
• Решение задач статики для тел, на которыедействует система параллельных сил
• Ввести понятие пары сил
• Сформулировать основную теорему статики
План лекции
3.1. Параллельные силы, направленные в одну сторону
3.2. Параллельные силы, направленные
противоположно
3.3. Теория пар сил
3.4. Основная теорема статики
3.5. Условия равновесия СПС
3.6. Заключение
4
5. 3.1. Определение СПС
6. 3.1.1. Определение и примеры
Система сил, линии действия которыхпараллельны, называются системой
параллельных сил (СПС)
2.1.
ССС
3.1.ОПРЕДЕЛЕНИЕ
ПС, НАПРАВЛЕННЫЕ
В ОДНУ СТОРОНУ
5
7.
3.1.2. Теорема о равнодействующей двух силС и с те ма дву х па ра л ле л ьн ы х с и л ,
направленных в одну сторону, имеет
равнодействующую, равную по модулю
сумме их модулей, параллельна им и
направленную в ту же сторону.
Линия действия равнодействующей делит
отрезок между точками приложения
данных сил обратно пропорционально их
величине
2.1.
ССС
3.1. ОПРЕДЕЛЕНИЕ
ПС, НАПРАВЛЕННЫЕ
В ОДНУ СТОРОНУ
6
8. Теорема о равнодействующей двух сил
3.1.2. Теорема о равнодействующейдвух сил
Теорема о равнодействующей
двух сил
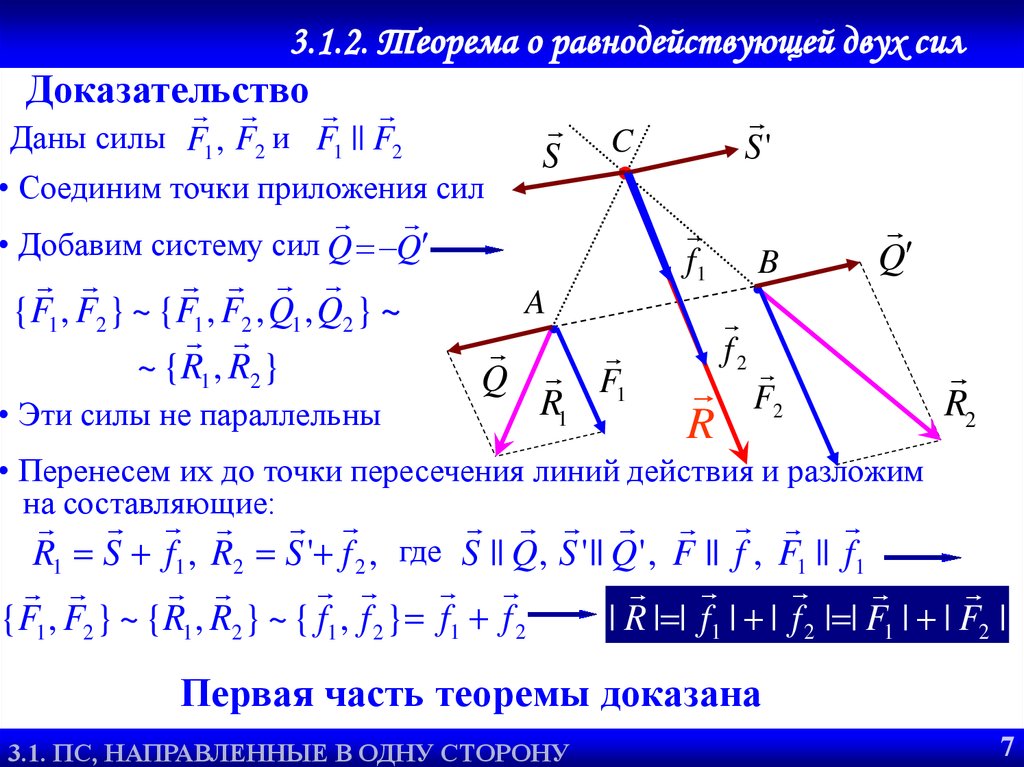
Доказательство
Даны силы F1 , F2 и F1 || F2
S
• Соединим точки приложения сил
• Добавим систему сил Q Q
{F1 , F2 } ~ {F1 , F2 , Q1 , Q2 } ~
~ {R1 , R2 }
• Эти силы не параллельны
S'
C
f1
A
Q
R1
F1
R
B
f2
Q
F2
R2
• Перенесем их до точки пересечения линий действия и разложим
на составляющие:
R1 S f1 , R2 S ' f 2 , где S || Q, S ' || Q ' , F || f , F1 || f1
{F1 , F2 } ~ {R1 , R2 } ~ { f1 , f 2 } f1 f 2
| R | | f1 | | f 2 | | F1 | | F2 |
Первая часть теоремы доказана
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ
СИЛСТОРОНУ
3.1.
ПС, НАПРАВЛЕННЫЕ
В ОДНУ
78
9. Теорема о равнодействующей двух сил
Теорема о равнодействующейсил
Теорема о3.1.2.
равнодействующей
двухдвух
сил
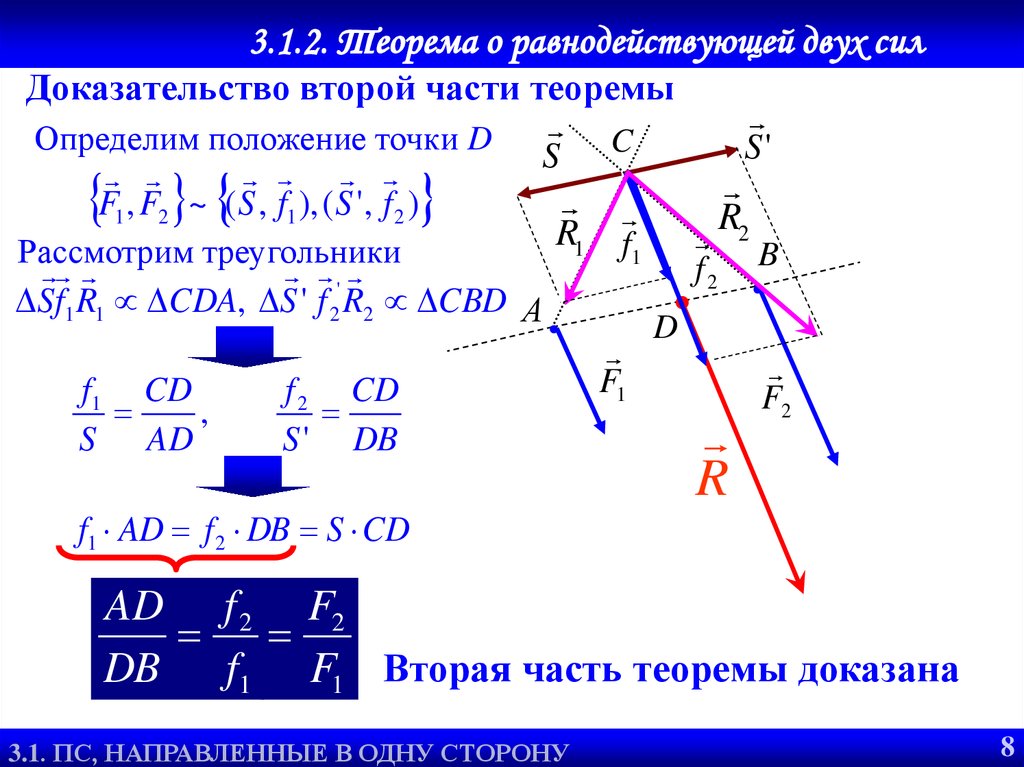
Доказательство второй части теоремы
Определим положение точки D
C
S'
S
F1 , F2 ~ ( S , f1 ), ( S ' , f 2 )
R2
R
f1
1
Рассмотрим треугольники
f2 B
'
Sf1 R1 CDA, S ' f 2 R2 CBD А
f1 CD
,
S AD
f 2 CD
S ' DB
f1 AD f 2 DB S CD
F1
D
R
F2
AD f 2 F2
DB f1 F1 Вторая часть теоремы доказана
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ
СИЛСТОРОНУ
3.1.
ПС, НАПРАВЛЕННЫЕ
В ОДНУ
89
10. Равнодействующая СПС
3.1.3.Центр параллельных сил
Равнодействующая
СПС
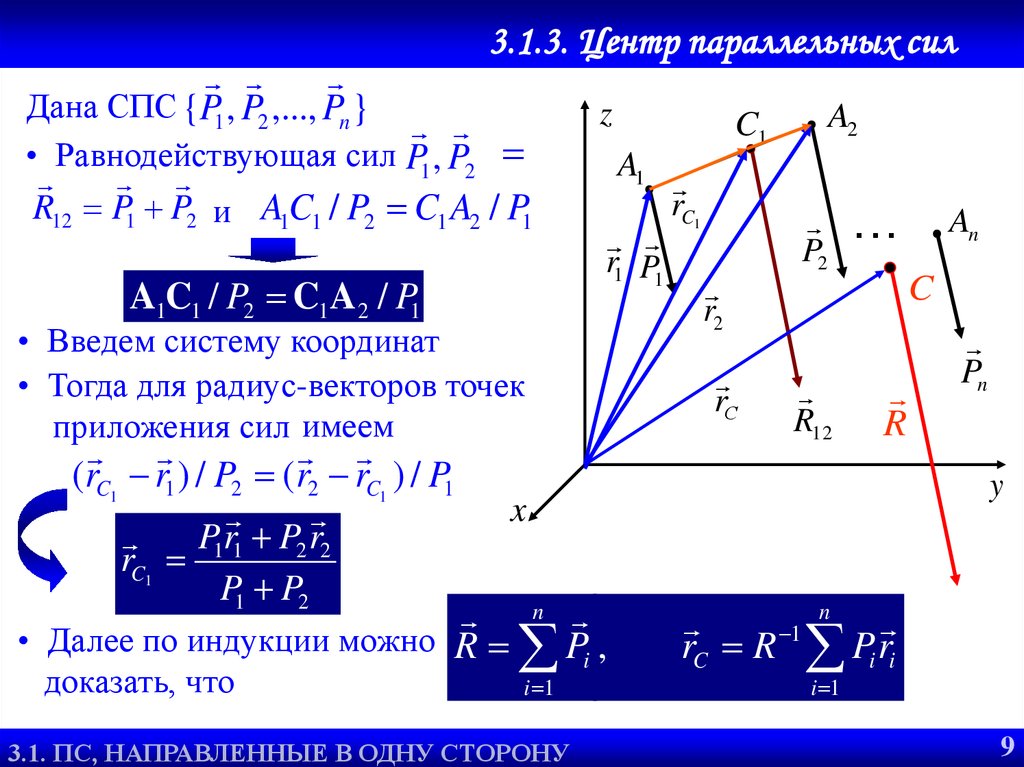
Дана СПС {P1 , P2 ,..., Pn }
• Равнодействующая сил P1 , P2
R12 P1 P2 и A1C1 / P2 C1 A2 / P1
A1C1 / P2 C1A 2 / P1
z
A1
r1 P1
• Введем систему координат
• Тогда для радиус-векторов точек
приложения сил имеем
(rC1 r1 ) / P2 (r2 rC1 ) / P1
P1r1 P2 r2
rC1
P1 P2
rC1
r2
rС
P2
...
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ
СИЛ
3.1.
ПС, НАПРАВЛЕННЫЕ
В ОДНУ СТОРОНУ
An
C
R12
R
Pn
y
x
n
• Далее по индукции можно R Pi ,
доказать, что
A2
C1
n
1
rC R Pi ri
i 1
119
11. Распределенные силы
3.1.4. Распределенные силыРаспределенные силы
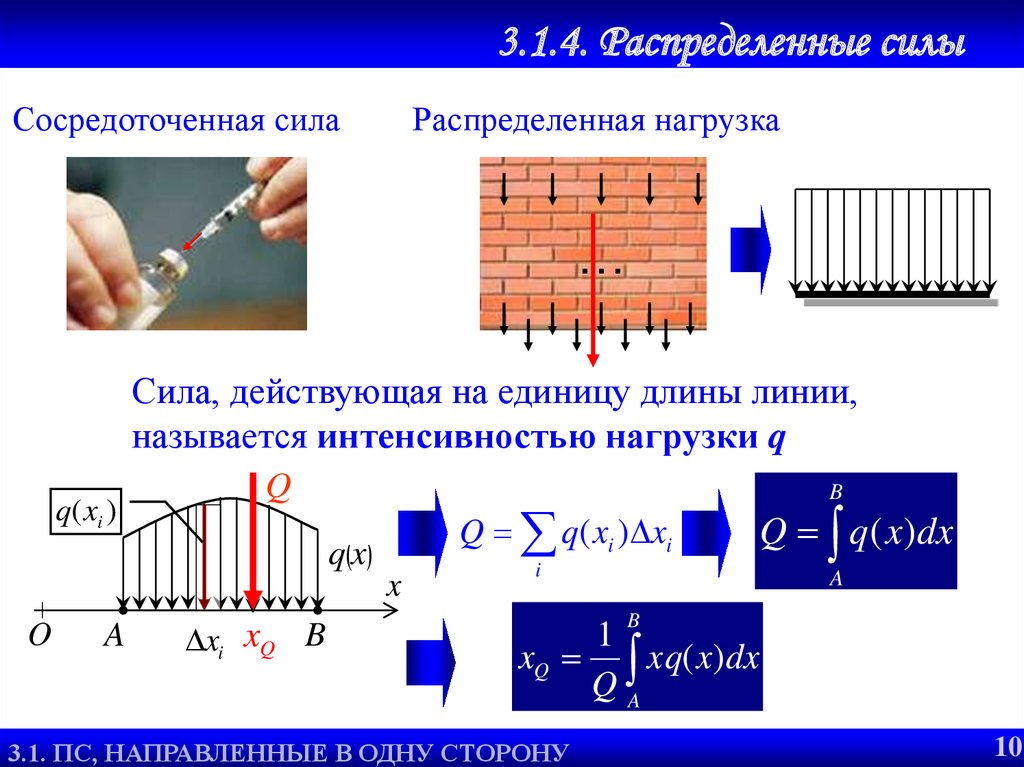
Сосредоточенная сила
Распределенная нагрузка
…
Сила, действующая на единицу длины линии,
называется интенсивностью нагрузки q
Q
B
q( xi )
Q q( xi ) xi
Q q ( x)dx
q x
x
O
A
xi xQ B
i
A
B
1
xQ xq( x)dx
QA
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ
СИЛ
3.1.
ПС, НАПРАВЛЕННЫЕ
В ОДНУ СТОРОНУ
10
13
12. Распределенные силы. Два примера
3.1.4. РаспределенныеДва примера
Распределенные
силы. Два силы.
примера
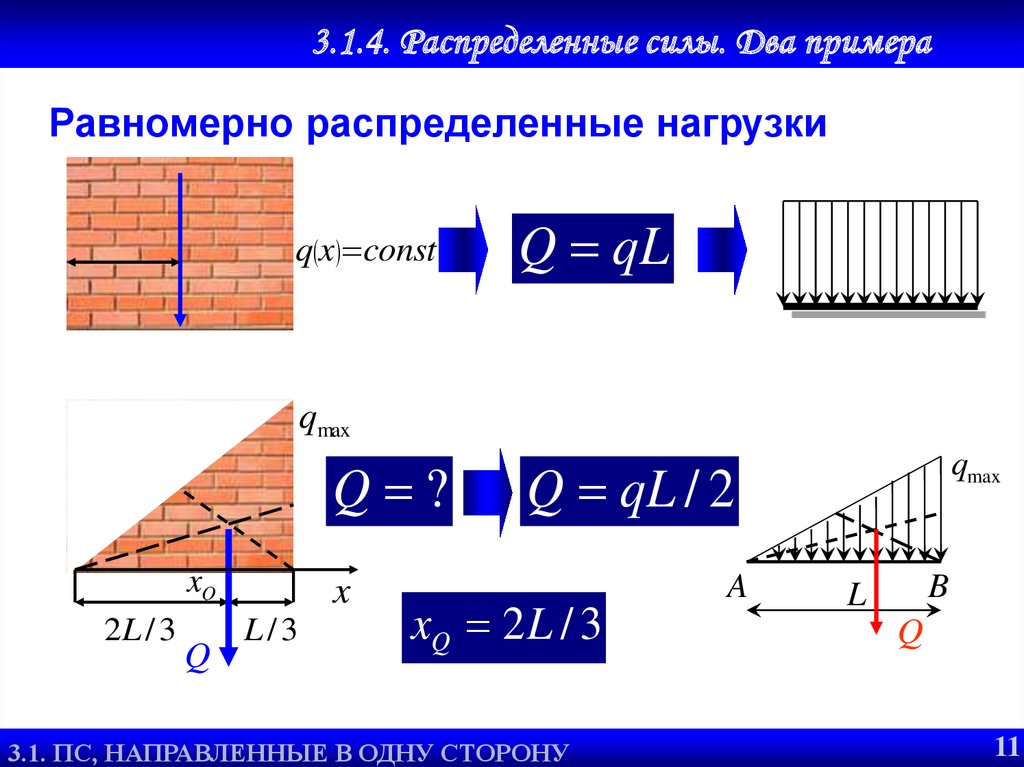
Равномерно распределенные нагрузки
L/2
Q
q x const
Q qL
qmax
Q ?
xQ
2L / 3
Q
x
L/3
Q qL / 2
xQ 2L / 3
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ
СИЛ
3.1.
ПС, НАПРАВЛЕННЫЕ
В ОДНУ СТОРОНУ
A
qmax
B
L
Q
11
14
13. 3.2. Параллельные силы, направленные противоположно
14.
3.2.1. Теорема о равнодействующей двух силСистема двух не равных по модулю сил, линии
действ ия которых пара ллельны, н о силы
направлены противоположно, имеет
равнодействующую, которая равна по модулю
разности модулей этих сил, им параллельна и
направлена в сторону большей силы.
Линия действия равнодействующей проходит
через точку, которая лежит на продолжении
отрезка АВ и делит этот отрезок внешним образом
на части, обратно пропорциональные силам
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
СПС, НАПРАВЛЕННЫЕ
ПРОТИВОПОЛОЖНО
12
15.
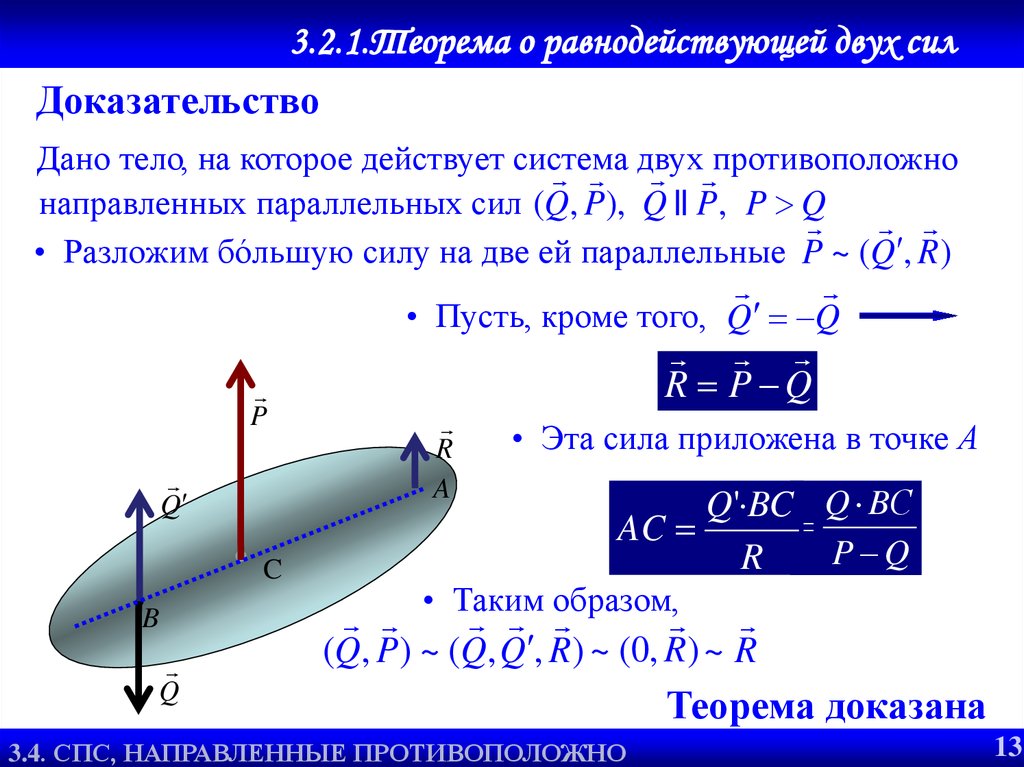
3.2.1.Теорема о равнодействующей двух силДоказательство
Дано тело, на которое действует система
двух
противоположно
направленных параллельных сил (Q, P ), Q || P, P Q
• Разложим бóльшую силу на две ей параллельные P ~ (Q , R )
• Пусть, кроме того, Q Q
P
Q
C
B
Q
R P Q
R
A
• Эта сила приложена в точке А
Q' BC Q BС
AC
P Q
R
• Таким
образом,
(Q, P ) ~ (Q, Q , R ) ~ (0, R ) ~ R
2.1.
СССсил, направленных
Сложение
в разные стороны
3.4. ОПРЕДЕЛЕНИЕ
СПС,параллельных
НАПРАВЛЕННЫЕ
ПРОТИВОПОЛОЖНО
Теорема доказана
13
16. 3.3. Теория пар сил
17.
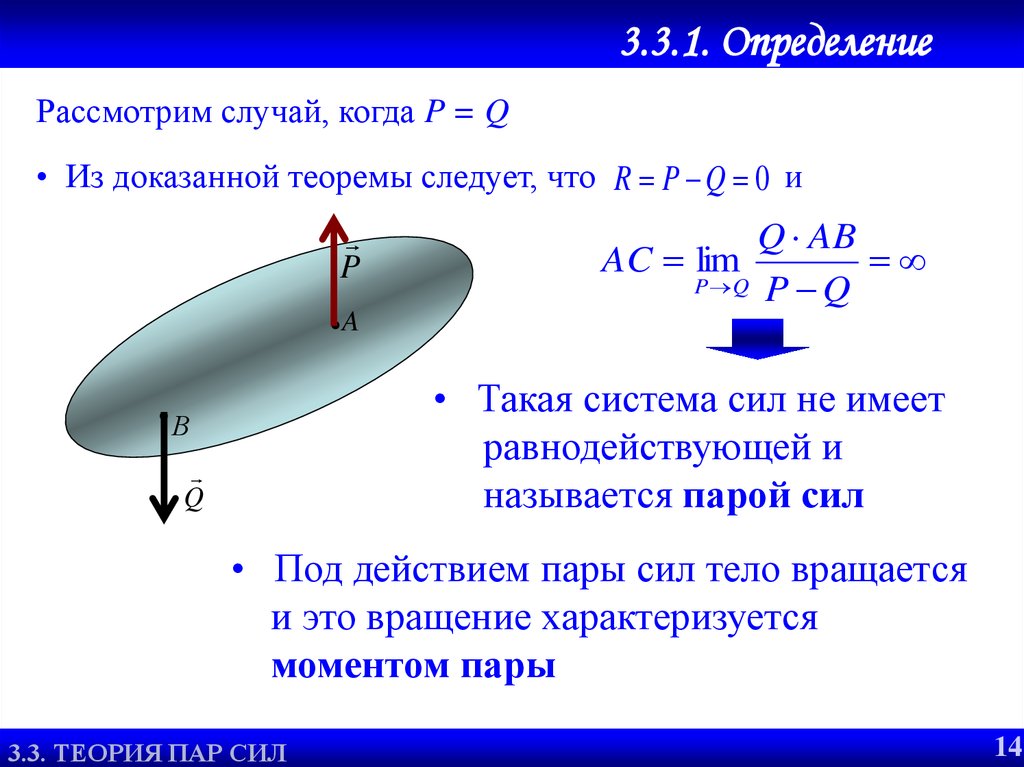
3.3.1. ОпределениеРассмотрим случай, когда P = Q
• Из доказанной теоремы следует, что R P Q 0 и
P
Q AB
AC lim
P Q P Q
A
• Такая система сил не имеет
равнодействующей и
называется парой сил
В
Q
• Под действием пары сил тело вращается
и это вращение характеризуется
моментом пары
2.1.
ССС
ПАРА
СИЛ
3.3. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР СИЛ
14
18.
3.3.2. Момент парыM
Пусть дана пара сил ( F , F1 )
F1
• Плоскость, проходящая через линии
действия сил, называется плоскостью
А
действия пары
B
• Расстояние между линиями действия
F
сил называется плечом пары
Моментом пары сил называется вектор M , модуль которого равен
произведению модуля одной из сил пары на плечо пары: M=Fd. Этот
вектор направлен перпендикулярно плоскости действия пары в сторону,
откуда вращение пары видно происходящим против часовой стрелки.
Для пар сил, расположенных в одной плоскости можно использовать
понятие алгебраического момента пары: M = ±Fd. Знак "плюс" берется,
если пара стремится повернуть тело против хода часовой стрелки,
"минус" – по ходу.
Момент пары не зависит от точек приложения сил пары.
Он определяется лишь плечом пары
2.1.
ССС
ПАРА
СИЛ
3.3. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР СИЛ
15
19. Доказательство
3.3.3. Теорема об эквивалентности пар силДоказательство
Все пары сил, имеющие один и тот же момент,
эквивалентны.
Доказательство Дана пара сил ( F , F ) с моментом m = Fh
Q
A
d
f
F
C
h
Q
F
B
• Разложим каждую из них по двум
направлениям на силы { f , Q},{ f , Q }
( F , F ) ~ ( f , Q, f , Q ) но ( f , f ) ~ 0
f
( F , F ) ~ (Q, Q )
• Момент пары (Q, Q ) равен m Qd
Так как ABC ~ FQf то d hF Q
m Qd (Qh ) F / Q Fh m
Теорема доказана для пар, лежащих в одной плоскости
2.1.
ССС
ТЕОРЕМА
ОБ ЭКВИВАЛЕНТНОСТИ
ПАР СИЛ
3.3. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР СИЛ
16
20.
3.3.4. Пары сил. Итоги• Таким образом, действие на тело пары сил целиком
определяется ее моментом
• Действие всех пар, имеющих одинаковые моменты
эквивалентны
• Располагать пару сил в пространстве можно в любом
месте. Момент пары сил поэтому называют
свободным вектором
• Если пары сил лежат в одной
плоскости, то их моменты
перпендикулярны этой плоскости
и можно использовать понятие
алгебраического момента пары
ТЕОРЕМА
ОБ ЭКВИВАЛЕНТНОСТИ
ПАР СИЛ
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР СИЛ
m2
m1
m3
17
21. Доказательство
3.3.5. Теорема об сложении пар силДоказательство
Действие на тело системы пар с моментами M 1 , M 2 ,..., M N
Эквивалентно действию одной пары с моментом
Q1
R1
A
F1
B
R1
N
M Mk
Q1
k 1
• Докажем сначала теорему для двух пар сил
• Из теоремы об эквивалентности пар следует, что
F1
для доказательства достаточно рассмотреть две
пары, точки приложения сил которых A и B
совпадают
• Рассмотри две пары сил ( F1 , F1 ) и (Q1 , Q1 )
• Действие рассматриваемых
двух пар эквивалентно
действию одной пары ( R1 , R1 ) с моментом
M AB R1 AB ( F1 Q1 ) AB F1 AB Q1 M 1 M 2
Для N пар доказательство получается по индукции.
ТЕОРЕМА
О СЛОЖЕНИИ
2.1.
ССС ПАР СИЛ
3.3. ОПРЕДЕЛЕНИЕ
ТЕОРИЯ
ПАР СИЛ
18
22. 3.3.6. Уравнения равновесия тела под действием системы пар
• Действие на телосистемы пар сил с
произвольной
моментами M 1 , M 2 ,..., M N эквивалентно
действию
N
одной пары с моментом M M k
k 1
• Для того чтобы тело под действием системы пар тело
находилось в равновесии, необходимо и достаточно,
чтобы
N
M Mk 0
k 1
Уравнения равновесия
N
M x M kx 0,
k 1
M y M ky 0,
Для плоской системы сил
3.3.УСЛОВИЯ
ТЕОРИЯ РАВНОВЕСИЯ
ПАР СИЛ
2.2.
N
k 1
N
M z M kz 0
k 1
N
m
k 1
k
0
19
23. Условия равновесия тела под действием системы пар сил
Условия равновесия тела под3.3.7. Задача 3.1
В плоскости Оxy расположены
три пары
Определить момент
действием
системы
парсил.
сил
пары m3, при котором эта система пар находится в равновесии,
если m1 = 510 Н·м, m2 = 120 Н·м
Решение
y
m1
m2
m3
Уравнение равновесия данной
системы пар имеет вид
m1 + m2 – m3 = 0
O
x
510 120 m3 0
Условия
равновесия
под действием системы пар сил
3.3.УСЛОВИЯ
ТЕОРИЯ
ПАРтела
СИЛ
2.2.
РАВНОВЕСИЯ
m3 670 Н м
20
24. 3.3.8. Еще один тип связи
• Жесткая заделка – это вид связи, полностью запрещающейдвижение тела
• Пример – балка, один конец которой защемлен
• Реакция жёсткой заделки представляет собой совокупность
силы и пары сил, которые образуют плоскую или
пространственную систему сил в зависимости от того,
какими являются активные силы.
Графическое представление
Реакция жесткой заделки
y
YA
А
mA
3.3. РЕШЕНИЯ
ТЕОРИЯ ПАР
СИЛСТАТИКИ
2.5.
ЗАДАЧ
2.2.
УСЛОВИЯ
РАВНОВЕСИЯ
XA
x
21
25. 3.4. Основная теорема статики (теорема Пуансо)
26.
Луи Пуансо1777-1859, Париж
22
27. 3.4.1. Лемма о параллельном переносе силы
Действие на твердое тело силы F , приложенной в точкеA, эквивалентно действию силы F ' , равной исходной по
модулю, параллельной ей и приложенной в точке В, и
паре сил с моментом равным моменту данной силы
относительно точки В
F'
F'
В
F
A
Доказательство
• Добавим к силе
F уравновешенную
систему сил {F ' , F '} ~ 0 в точке В
F ~ {F , F ' , F '}
• Но силы F , F ' образуют пару сил с
моментом
M ( F , F ' ) BA F M B ( F )
Теорема доказана
2.1.
ССС
3.4. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
23
28. 3.4.2. Иллюстрация
QА
Q
B
P
Чтобы удержать однородный
брусок весом P за его середину,
нужно просто тянуть его вверх
с силой Q = P
2.1.
ССС
3.4. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
m А
B
P
Чтобы удержать однородный
брусок весом P в равновесии за
конец А, необходимо не только
тянуть его вверх с силой Q = P,
но и создавать момент m = P·AB/2
24
29.
3.4.3. Главный векторГлавным
*вектором данной системы сил называется
вектор R , равный сумме всех сил системы
* n
R Fi
i 1
Замечание
• Главный вектор определен для любой системы, а равнодействующая в ряде случаев просто не существует
• Главный вектор системы сил не зависит от центра
приведения
2.1.
ССС
3.4. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
25
30.
3.4.3. Главный моментГлавным моментом данной системы сил относительно
*
точки А называется вектор M A , равный сумме моментов
всех сил системы относительно той же точки
n
n
*
M A M Ai M A ( Fi )
i 1
i 1
Замечание
• Главный момент
меняется
при смене центра
приведения
Действительно, M Ai rAK Fi , а M Bi rBK Fi
n
n
**
Fi
M A ( Fi ) rAK Fi
M
MAA
rAK
i 1
i 1
А
К
rАВ
rВK
B
n
n
(rAB rBK ) Fi rAB Fi rBK Fi
i 1
i 1
i 1
rAB R* M B*
n
2.1.
ССС
3.4. ОПРЕДЕЛЕНИЕ
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
26
31. Теорема о равнодействующей двух сил
3.4.4. Теорема Пуансо(1804
Теорема о равнодействующей
двух
силг.)
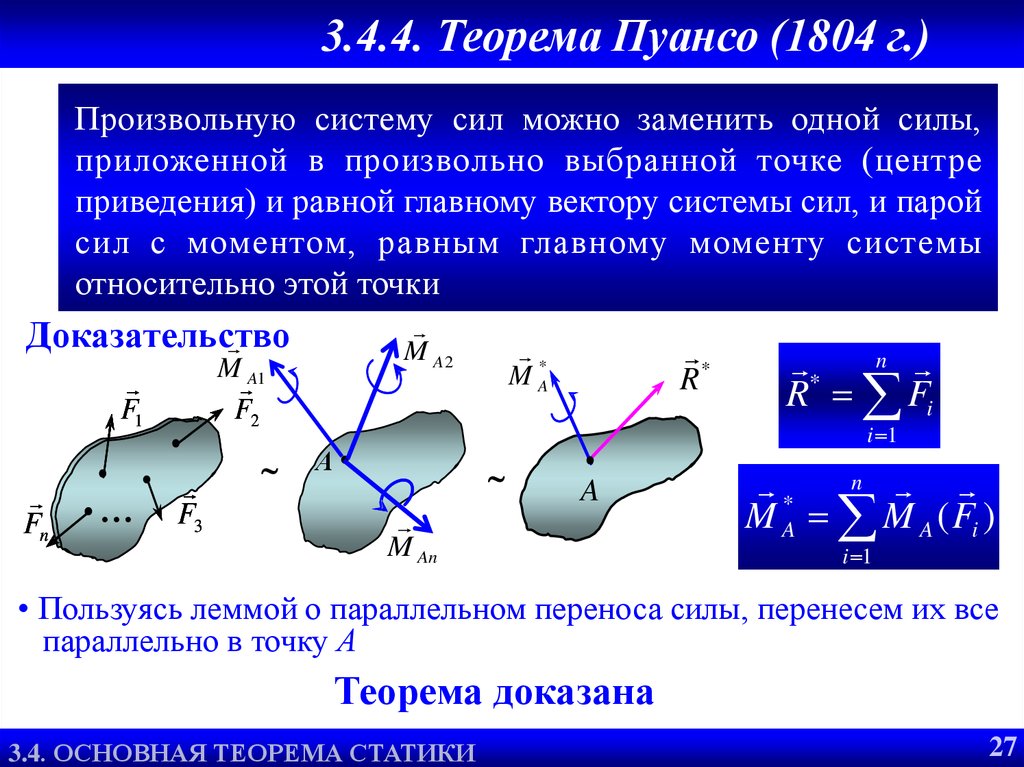
Произвольную систему сил можно заменить одной силы,
приложенной в произвольно выбранной точке (центре
приведения) и равной главному вектору системы сил, и парой
сил с моментом, равным главному моменту системы
относительно этой точки
M A2
Доказательство
M A1
F1
Fn
…
F2
F3
*
R
*
MA
* n
R Fi
i 1
~
А
~
M An
A
n
*
M A M A ( Fi )
i 1
• Пользуясь леммой о параллельном переноса силы, перенесем их все
параллельно в точку А
Теорема доказана
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ
СИЛ
3.4.
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
27
8
32. Теорема о равнодействующей двух сил
3.4.5. Критерий эквивалентностиДля того чтобы две системы сил, приложенные к
твердому телу, были эквивалентны, необходимо и
достаточно, чтобы они имели одинаковые главные
векторы и главные моменты
Основная теорема статики является конструктивной, она дает
простой способ аналитического определения главного
вектора и главного момента любой системы сил
n
n
* * * *
R i Rv j Rv k Rv Fi i Fix j Fiy k Fiz
i 1
i 1
n
n
*
* * *
M A i M Ax j M Ay k M Az M A ( Fi ) i M Ax ( Fi ) j M Ay ( Fi ) k M Az ( Fi )
n
i 1
i 1
i 1
i M x ( Fi ) j M y ( Fi ) k M z ( Fi )
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ
СИЛ
3.4.
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
28
8
33. Теорема о равнодействующей двух сил
3.4.6. двухЗадача
3.2
Теорема о равнодействующей
сил
Привести к центру О систему сил P, F1 , F2 , F3 , действующих на
пластину длиной 2b, если Р = 30 Н, F1 = F2 = F3 = 20 Н, а = 0,3 м,
b = 0,5 м, = 60°.
y
F1
Решение
F2 F
3
a
• Введем систему координат с
началом в точке О
• Найдем главный вектор
O
x
P
данной системы сил
Rx* F1 cos F2 cos F3 40 (H),
R*y F1 sin F2 sin P 30 (H)
• Найдем теперь главный момент данной системы сил. Эта
система плоская, поэтому момент имеет единственную
составляющую, перпендикулярную плоскости чертежа
M O* aF1 cos 2bF2 sin aF3 bP 11.3 (H м)
2.1.
ССС
3.2. ОПРЕДЕЛЕНИЕ
РАВНОДЕЙСТВУЮЩАЯ
ДВУХ
СИЛ
3.4.
ОСНОВНАЯ ТЕОРЕМА
СТАТИКИ
29
8
34. 3.5. Условия равновесия произвольной системы сил
35. Равнодействующая СПС
3.5.1. УравненияРавнодействующая
СПС равновесия
Пусть дана произвольная система сил {F1, F2 ,..., Fn }. Тело под
действием этой системы
в равновесии, если она
сил находится
эквивалента нулю {F1 , F2 ,..., Fn } ~ 0
Но
{F1, F2 ,..., Fn } ~ {R* , M O* )} ~ 0
n
* n
*
R Fi 0,
M O M Oi 0
i 1
i 1
В координатной форме эти уравнения равновесия имеют вид
n
F
i 1
ix
i 1
F
0,
M x ( Fi ) 0,
n
n
i 1
iy
0,
M y ( Fi ) 0,
n
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ СИЛ
3.5.
УСЛОВИЯ
РАВНОВЕСИЯ
n
F
iz
i 1
0
M z ( Fi ) 0
n
i 1
30
11
36. Равнодействующая СПС
3.5.2. УравненияРавнодействующая
СПСравновесия СПС
Пусть дана параллельных сил в пространстве (линии действия
параллельны оси Oz. Главный вектор в этом случае имеет
единственную составляющую, параллельную этой оси, поэтому
n
F
i 1
iz
0
Моменты же всех сил относительно оси Oz равны нулю, и
следовательно,
M x ( Fi ) 0,
n
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ СИЛ
3.5.
УСЛОВИЯ
РАВНОВЕСИЯ
M y ( Fi ) 0
n
i 1
31
11
37. Равнодействующая СПС
3.5.3. УравненияРавнодействующая
СПСравновесия ПСС
Пусть все силы находятся в плоскости Oxy. В этом случае проекция
главного вектора на ось Oz равна нулю, а главный момент направлен
параллельно этой оси. Т.о., имеем три уравнения равновесия.
Основная форма уравнений равновесия ПСС
n
F
i 1
ix
0,
n
F
iy
i 1
0,
M А ( Fi ) 0
n
i 1
Вторая форма уравнений равновесия ПСС (АВ
M А ( Fi ) 0,
n
i 1
M В ( Fi ) 0,
n
i 1
n
F
i 1
ix
Ox)
0
Третья форма уравнений равновесия ПСС (точки А, В, С не
должны лежать на одной прямой)
n
n
n
M А ( Fi ) 0, M В ( Fi ) 0, M С ( Fi ) 0
i 1
i 1
2.1.
ССС
3.3. ОПРЕДЕЛЕНИЕ
ЦЕНТР
СИСТЕМЫ
ПАРАЛЛЕЛЬНЫХ СИЛ
3.5.
УСЛОВИЯ
РАВНОВЕСИЯ
i 1
32
11
38. 3.6. Заключение
39. 3.6.1. Основные выводы
• Две сонаправленные силы, линии действия которыхпараллельны имеют равнодействующую
• Две параллельные противоположно направленные и
не равные по модулю силы имеют равнодействующую
• Введено понятие пары сил, действие которой
характеризуется ее моментом
• Действие на тело произвольной системы сил
всегда можно заменить действием одной силы
равной главному вектору и одной парой с
моментом, равным главному моменту
• Для произвольной системы сил в общем случае
можно составить 6 уравнений равновесия
3.6.
ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
1.2. ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
33
40. 3.6.2. Тема следующей лекции
РАВНОВЕСИЕСИСТЕМЫ ТЕЛ
1.3.
СТАТИКИ
3.6.АКСИОМЫ
ЗАКЛЮЧЕНИЕ
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
34
41. 3.6.2. Тема следующей лекции
1.3.СТАТИКИ
3.6.
ЗАКЛЮЧЕНИЕ
1.2. АКСИОМЫ
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
35
42. 3.6.2. Тема следующей лекции
1.3.СТАТИКИ
3.6.АКСИОМЫ
ЗАКЛЮЧЕНИЕ
1.2.
ОСНОВНЫЕ
ПОНЯТИЯ И МОДЕЛИ
37


































 physics
physics








