Similar presentations:
Теория пар сил
1.
Новосибирский Государственный Архитектурно-СтроительныйУниверситет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 5.
ТЕОРИЯ ПАР СИЛ
Кафедра теоретической механики
2. План лекции
ВведениеСложение параллельных сил, направленных
в разные стороны
Пара сил. Момент пары сил
Теорема об эквивалентности пар сил
Теорема о сложении пар сил
Условие равновесия тела под действием
системы пар сил
Заключение
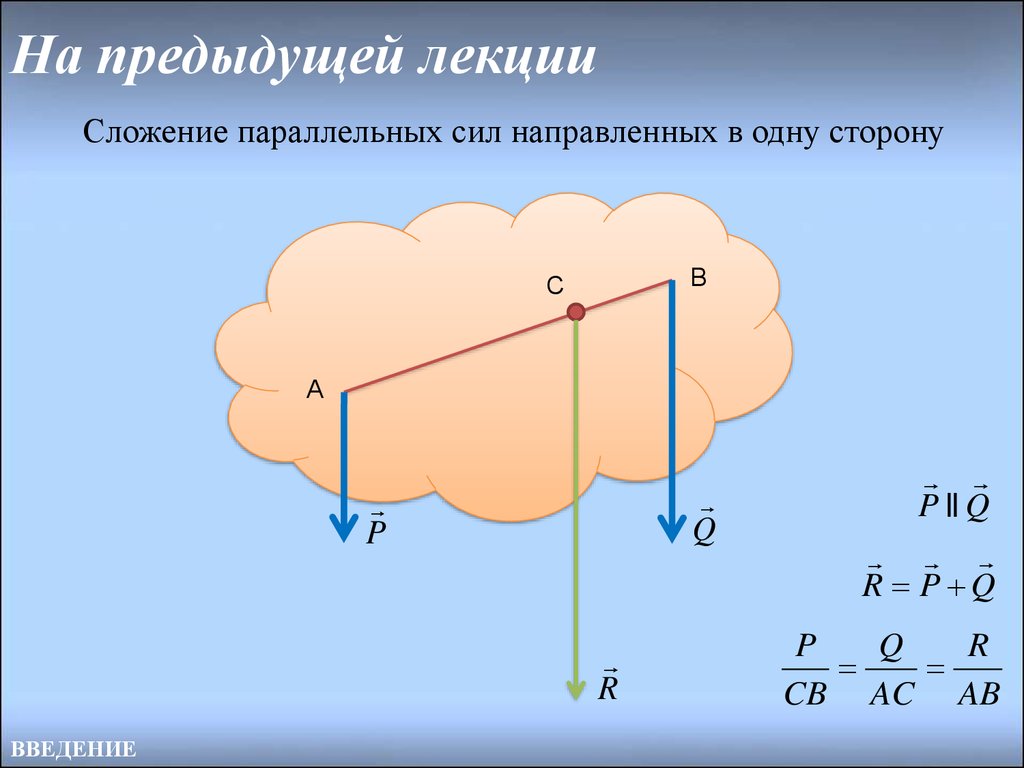
3. На предыдущей лекции
Сложение параллельных сил направленных в одну сторонуB
C
A
Q
P
R
ВВЕДЕНИЕ
P || Q
R P Q
P
Q
R
CB AC AB
4. Цель лекции
Научиться работать спарами сил.
ВВЕДЕНИЕ
5. Актуальность. Практические примеры
…что тело под действием одной силы F (~системе сходящихся сил)Движется прямолинейно и
равноускоренно.
… что тело под действием системы параллельных сил
Движется прямолинейно и
равноускоренно.
ВВЕДЕНИЕ
6. Актуальность. Практические примеры
В этой лекции вы узнаете…Какую систему сил необходимо приложить, чтобы заставить
тело вращаться
ВВЕДЕНИЕ
7. Теорема о сложении двух сил, направленных в разные стороны, но линии действия которых параллельны
Система двух не равных по модулю сил, линиидействия которых параллельны, но силы
направлены противоположно, имеет
равнодействующую, которая равна по модулю
разности модулей этих сил, им параллельна и
направлена в сторону большей силы. Линия
действия равнодействующей проходит через
точку, которая лежит на продолжении отрезка АВ
и делит этот отрезок внешним образом на части,
обратно пропорциональные силам.
Сложение параллельных сил, направленных в разные стороны
8.
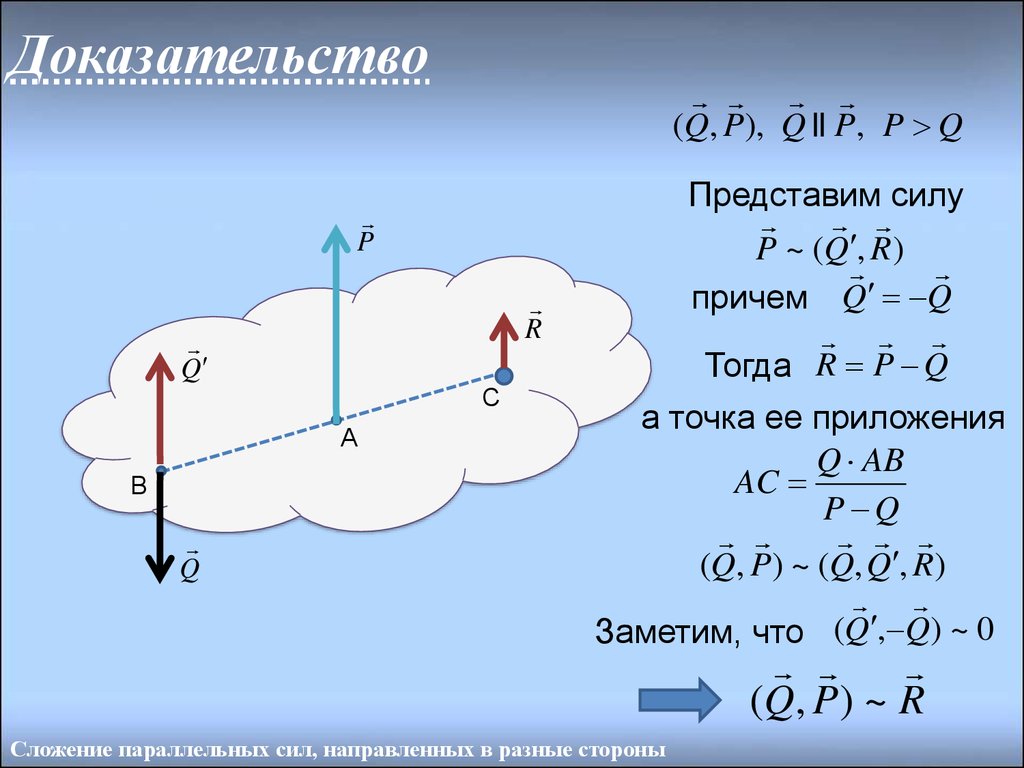
Доказательство(Q, P), Q || P, P Q
Представим силу
P ~ (Q , R )
причем Q Q
Тогда R P Q
P
R
Q
C
A
B
Q
а точка ее приложения
Q AB
AC
P Q
(Q, P) ~ (Q, Q , R)
Заметим, что (Q , Q) ~ 0
(Q, P ) ~ R
Сложение параллельных сил, направленных в разные стороны
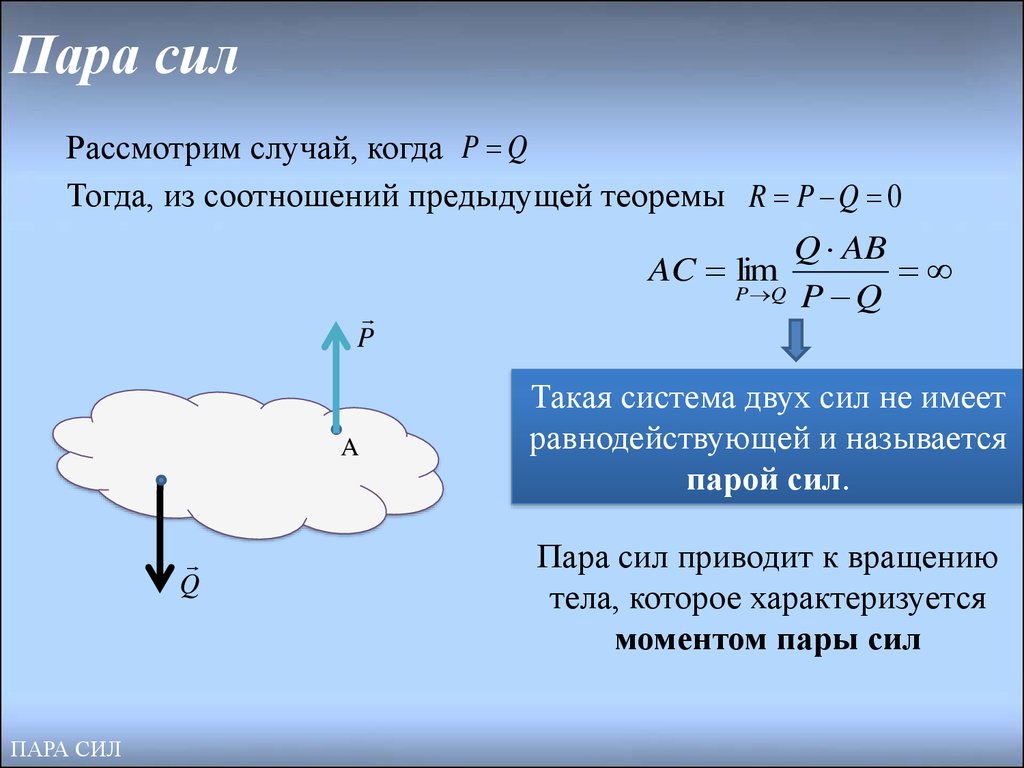
9. Пара сил
Рассмотрим случай, когда P QТогда, из соотношений предыдущей теоремы R P Q 0
P
A
Q
ПАРА СИЛ
Q AB
AC lim
P Q P Q
Такая система двух сил не имеет
равнодействующей и называется
парой сил.
Пара сил приводит к вращению
тела, которое характеризуется
моментом пары сил
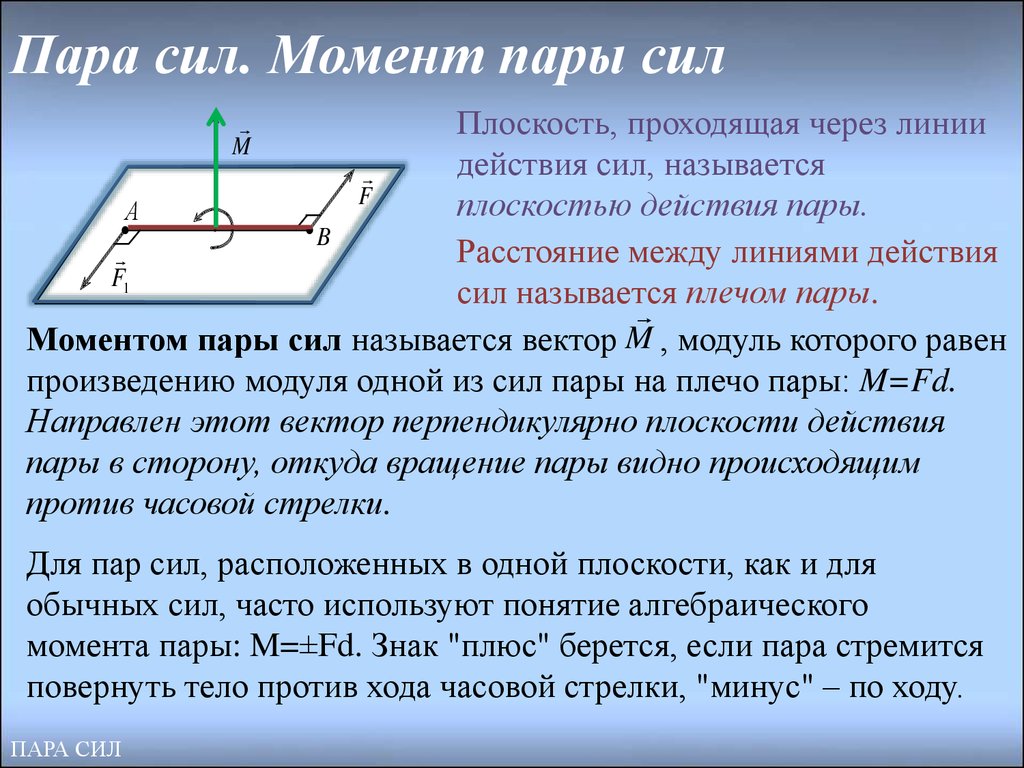
10. Пара сил. Момент пары сил
Плоскость, проходящая через линиидействия сил, называется
F
плоскостью действия пары.
А
B
Расстояние между линиями действия
F1
сил называется
плечом пары.
Моментом пары сил называется вектор M , модуль которого равен
произведению модуля одной из сил пары на плечо пары: M=Fd.
Направлен этот вектор перпендикулярно плоскости действия
пары в сторону, откуда вращение пары видно происходящим
против часовой стрелки.
M
Для пар сил, расположенных в одной плоскости, как и для
обычных сил, часто используют понятие алгебраического
момента пары: M=±Fd. Знак "плюс" берется, если пара стремится
повернуть тело против хода часовой стрелки, "минус" – по ходу.
ПАРА СИЛ
11. Пара сил. Вращательный эффект пары
Вращательный эффект парыF1
z
A
rA
F2
B
rB
O
y
x
складывается из вращательных
эффектов составляющих ее сил
M AB F2 (OB OA) F2
OB F2 OA F2 OB F2 OA F1
M O ( F1 ) M O ( F2 )
M M O ( F1 ) M O ( F2 )
Сумма моментов сил пары относительно любой точки О равна
моменту пары этих сил. Поскольку момент пары сил
перпендикулярен плоскости
пары, а его модуль равен
M AB F1 sin( AB, F1 ) , то момент пары не зависит от точек
приложения сил пары. Он определяется лишь плечом пары.
ПАРА СИЛ
12.
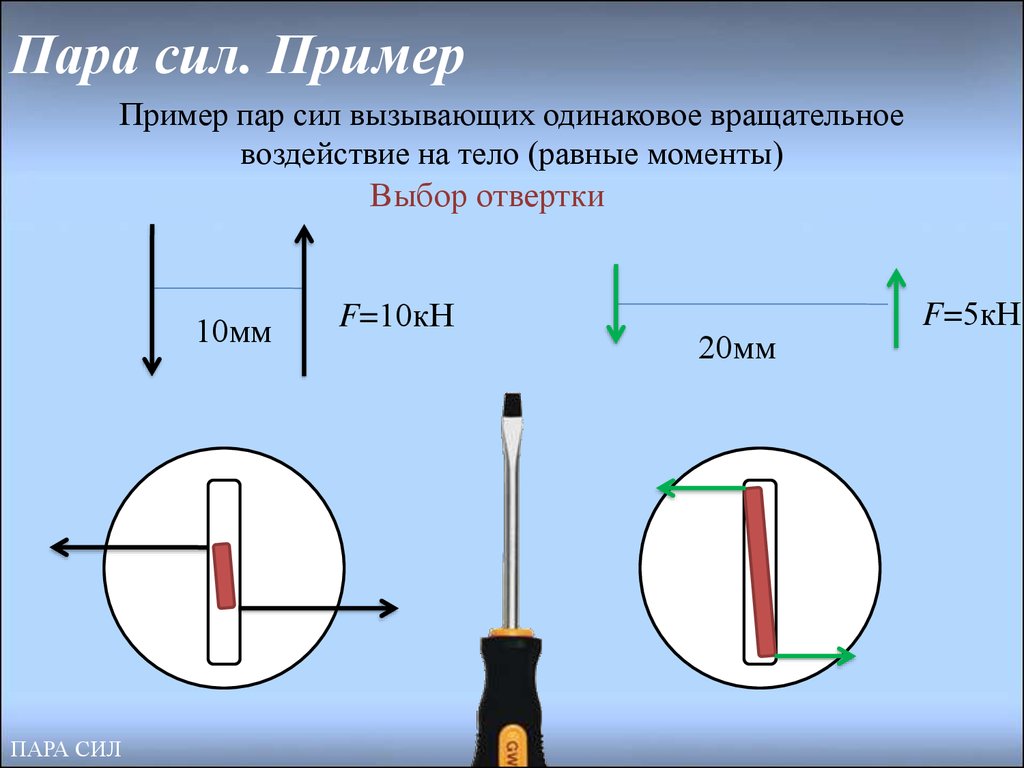
Пара сил. ПримерПример пар сил вызывающих одинаковое вращательное
воздействие на тело (равные моменты)
Выбор отвертки
10мм
ПАРА СИЛ
F=10кН
20мм
F=5кН
13.
Теорема об эквивалентности пар силВсе пары сил, имеющие один и тот
же момент, эквивалентны.
Доказательство проведем в два этапа:
1. Для случая когда плоскости действия пар совпадают.
2. Когда плоскости действия пар параллельны.
Так как вектор момента пары направлен перпендикулярно
плоскости действия пары, то равенство моментов
подразумевает, что плоскости действия пар либо совпадают
либо параллельны.
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
14. Доказательство
плоскости действия пар совпадаютПара сил ( F , F ) с моментом m Fh
( F , F ) ~ ( f , Q, f , Q )
Q F
A
h
F
Q
( f , Q, f , Q ) ~ (Q, Q )
C
d
f
Так как ( f , f ) ~ 0 то
B
f
Момент пары (Q, Q ) равен m Qd
Так как ABC ~ FQf то d hF Q
F
m Qd Qh Fh m
Q
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
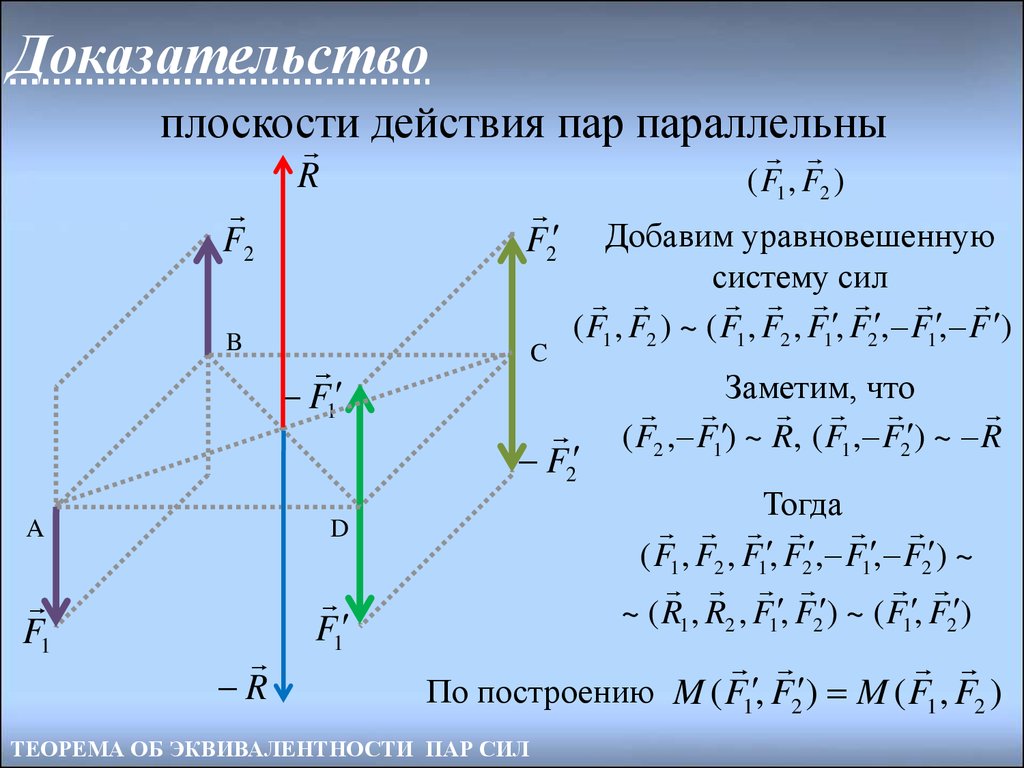
15. Доказательство
плоскостидействия пар параллельны
F2
B
R
F2
F1
A
D
F1
F1
R
C
( F1 , F2 )
Добавим уравновешенную
систему сил
( F1 , F2 ) ~ ( F1 , F2 , F1 , F2 , F1 , F )
F2
Заметим, что
( F2 , F1 ) ~ R, ( F1 , F2 ) ~ R
Тогда
( F1 , F2 , F1 , F2 , F1 , F2 ) ~
~ ( R1 , R2 , F1 , F2 ) ~ ( F1 , F2 )
По построению M ( F1 , F2 ) M ( F1 , F2 )
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
16.
Теорема об эквивалентности пар силПрименение теоремы об эквивалентности пар сил
Если нет крестовой отвертки, а есть только плоская с узким
шлицем. Воспользуемся теоремой и перенесем усилие…
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
17.
Теорема о сложении пар силДействие на тело системы пар с
моментами
M1 , M 2 ,..., M N
эквивалентно действию одной
пары с моментом
N
M Mk
k 1
ТЕОРЕМА О СЛОЖЕНИИ ПАР СИЛ
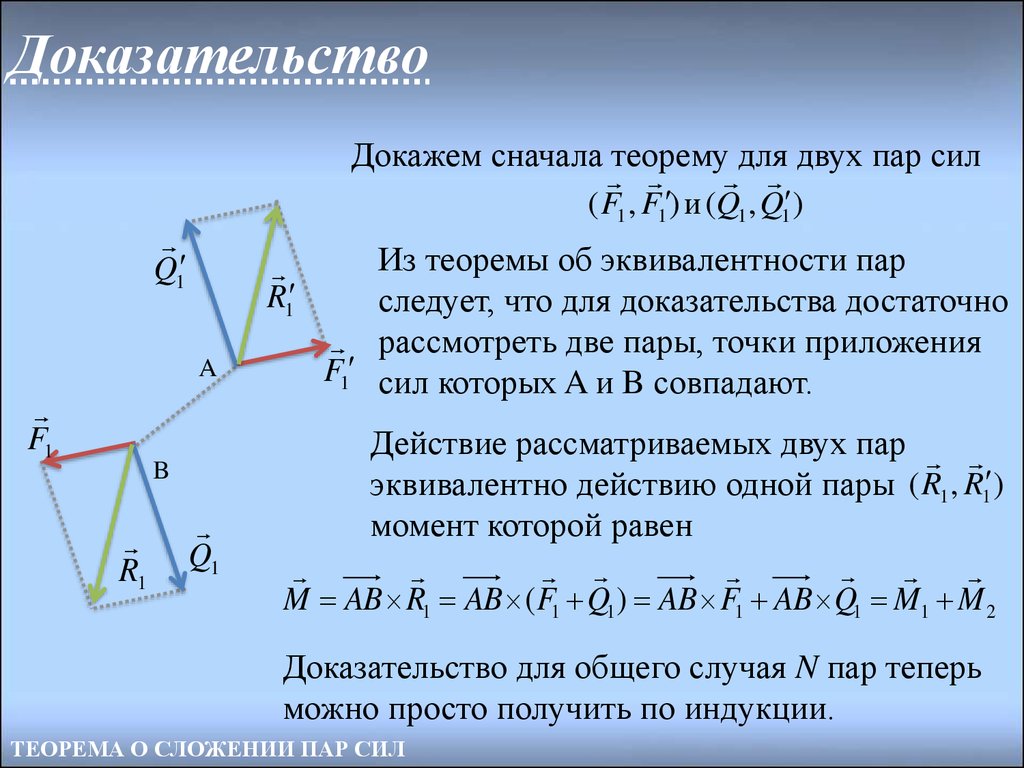
18. Доказательство
Докажем сначала теорему для двух пар сил( F1 , F1 ) и (Q1 , Q1 )
Q1
R1
A
F1
B
R1
Q1
Из теоремы об эквивалентности пар
следует, что для доказательства достаточно
рассмотреть две пары, точки приложения
F1 сил которых A и B совпадают.
Действие рассматриваемых двух пар
эквивалентно действию одной пары ( R1 , R1 )
момент которой равен
M AB R1 AB ( F1 Q1 ) AB F1 AB Q1 M1 M 2
Доказательство для общего случая N пар теперь
можно просто получить по индукции.
ТЕОРЕМА О СЛОЖЕНИИ ПАР СИЛ
19. Условия равновесия тела под действием системы пар сил
Для того чтобы тело под действием системы парM1 , M 2 ,..., M N находилось в равновесии, необходимо и
достаточно, чтобы результирующая пара была эквивалентна
нулю:
N
M Mk 0
k 1
Для проекций на оси координат получаем
три скалярных уравнения:
N
M x M kx 0
k 1
N
M y M ky 0
k 1
Условия равновесия тела под действием системы пар сил
N
M z M kz 0
k 1
20. Условия равновесия тела под действием системы пар сил
Пример решения задачиЗадача. В плоскости Оxy расположены три пары сил.
Определить момент пары m3, при котором эта система пар
находится в равновесии, если m1 = 510 Н·м, m2 = 120 Н·м
y
m1
m2
m3
Решение. Моменты пар m1, m2
положительны. Следовательно, уравнение
равновесия пар имеет вид:
510 120 m3 0
O
x
m3 670 Н м
Условия равновесия тела под действием системы пар сил
21. Вопросы для самоконтроля
1. В каком случае можно найти равнодействующую двухсил, направленных в противоположные стороны, линии
действия которых параллельны?
2. Чему равна эта равнодействующая?
3. Можно ли силу разложить на две ей параллельные, но
направленные противоположно?
4. Что такое пара сил?
5. Как найти плечо пары?
6. Чему равен момент пары?
7. Какие пары являются эквивалентными?
ЗАКЛЮЧЕНИЕ
22. Вопросы для самоконтроля
8. Почему момент пары сил называют свободным вектором?9. Как сложить пары?
10. Могут ли две эквивалентные пары иметь разные плечи?
11. Можно ли пару сил уравновесить одной силой?
12. Сформулируйте условия равновесия тела под действием
системы пар. Запишите уравнения равновесия тела под
действием системы пар.
ЗАКЛЮЧЕНИЕ
23. Тема следующей лекции
Приведение произвольнойсистемы сил к центру
ЗАКЛЮЧЕНИЕ

















 physics
physics mechanics
mechanics








