Similar presentations:
Решение систем показательных, логарифмических и линейных уравнений
1.
Решение системпоказательных,
логарифмических и
линейных уравнений
2.
Цель: научиться решать системыпоказательных, логарифмических и линейных
уравнений
Задачи:
1. Повторить правила решения показательных,
логарифмических уравнений.
2. Повторить материал школьного курса
математики, при решении систем линейных
уравнений.
3. Научиться решать системы уравнений
3.
1Основные свойства логарифмов
log a a 1
log a 1 0
c
log a a
c
1) log a b log a c log a b c
b
2) log a b log a c log a
c
k
3) k log a b log a b
4.
Основные свойства показательной функцииПри любых действительных значениях Х
справедливы равенства
а 0
х
1) а а
х1
х2
х1
а
х1 х2
а
х1 х2
2) х2 а
а
а
3) а
х1
х2
x
a
a
5) x
b
b
x
6) а 1
0
х1 х2
4) a b a b
х
x
x
x
1 1
х
7) х а
а
a
5.
2Способы решения линейных
уравнений
Система уравнений — это условие, состоящее в
одновременном выполнении нескольких
уравнений относительно нескольких (или одной)
переменных.
Другими словами, если задано несколько
уравнений с одной, двумя или больше
неизвестными, и все эти уравнения (равенства)
должны одновременно выполняться, такую
группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью
фигурной скобки
6.
1. Метод подстановких у 5
2 х 3 у 15
Нужно в одном из уравнений выразить одну
переменную через другие, а затем полученное
выражение подставить в остальные уравнения
вместо этой переменной.
Затем точно так же выражаем и подставляем
другую переменную и т.д., пока не получим
уравнение с одной переменной. После его
решения и нахождения одной из переменных последовательно возвращаемся к ранее
выраженным, подставляя найденные значения.
7.
1) Из первого уравнения выражаем Хх 5 у
2 х 3 у 15
2) Подставляем вместо Х во второе уравнение, находим У
2 (5 у ) 3 у 15
10 2 у 3 у 15
у 15 10
у 5
3) Возвращаемся к первому уравнению и находим Х
х 5 у 5 5 0
Ответ: х=0, у=5
8.
2. Метод алгебраического сложениях у 5
2 х 3 у 15
Основан на следующем: если сложить левые
части уравнений, то полученное выражение
будет равно сложенным правым частям этих
же уравнений, т.е.:
a b
a c b d
c d
9.
х у 52 х 3 у 15
Умножим первое уравнение на -2
2 х 2 у 10
2 х 3 у 15
Сложим первое и второе уравнение
2 х 2 х 2 у 3 у 10 15
у 5
Подставим У=5 в любое исходное уравнение
х у 5
х 5 5
х 0
Ответ: х=0, у=5
10.
2. Графический методПостроим графики каждого уравнения, в одной
системе координат. Решениями системы уравнений
будут точки пересечения графиков
х у 5
2 х 3 у 15
Для начала выразим У в каждом уравнении:
у 5 х
15 2 х
у
3
11.
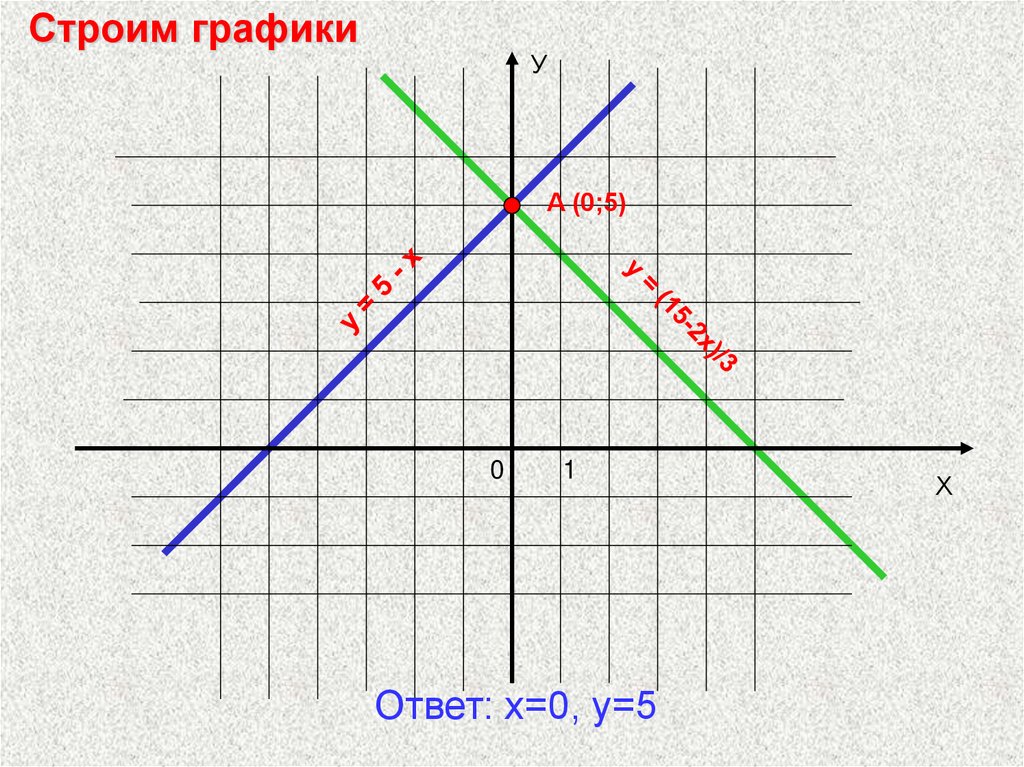
Строим графикиУ
А (0;5)
0
1
Ответ: х=0, у=5
Х
12.
3ПРИМЕРЫ
1) Решить систему
2 х у 1
х у
25
5
2 х у 1
х у
2
5
5
2 х у 1
х у 2
Ответ : (1;1)
2 х у 1
х 2 у
2 (2 у ) у 1
х 2 у
4 2у у 1
3 у 3
у 1
х 2 1 1
13.
2) Решить систему2 2 16
log 3 x log 3 y 1
2 x y 24
log 3 x y log 3 3
x y 4
x y 3
х
у
x 4 y
( 4 y ) y 3
2
4y y 3 0
y 4y 3 0
y1 3, y2 1
2
x1 1,
Ответ : (1; 3), ( 3; 1)
x2 3












 mathematics
mathematics








