Методы решения логарифмических уравнений

1.

2.

Основные сведения о логарифмах.

3.

Методы решения
логарифмических уравнений
1. Решение уравнений по свойствам
логарифма.
2. Решение уравнений по определению
логарифма
3. Решение уравнений заменой переменной.

4.

Решение логарифмического
уравнения по определению логарифма
log2 ( х 17 )
2
13
1. Решите уравнение:
Решение уравнения:
2
log2 ( х 17)
13
х – 17 = 13
х = 13 +17 = 30
2log2 (30 17) 13
log2 13
2
13
13=13
Ответ: х = 30
Пояснения и применяемые
формулы:
а
logа в
в
Перенесём число 2 в правую часть
Сделаем проверку
Посчитаем в скобках
а
logа в
в
Верно

5.

Решение логарифмического
уравнения по определению логарифма
3. Решите уравнение:
Решение уравнения:
lg x 3
lg x lg 10
3
1
lg x lg 3
10
Х= 1
103
Ответ: х = 0,001
lg x 3
Пояснения и применяемые формулы:
lg 10b b
a n
1
an
Левая и правая часть уравнения приведена
к логарифму по одному основанию

6.

Решение логарифмического
уравнения по определению логарифма
4. Решите уравнение: log 7 (5 x) 3
Решение уравнения:
Пояснения и применяемые формулы:
log 7 (5 x) 3
log a a b b
log 7 (5 x) log 7 7 3
Возведём 7 в куб
log 7 (5 x) log 7 343
5 - х = 343,
-x = 343 - 5
- x = 338
х = - 338
Левая и правая часть уравнения
приведена к логарифму по одному
основанию
Решим линейное уравнение
Неизвестные оставим в левой части,
числа переносим вправо
Умножим все части на (-1)

7.

Решение логарифмического
уравнения по свойствам логарифма
5. Решите уравнение: log 3 ( x 1) log 3 ( x 3) 1
Решение уравнения:
log 3 ( x 1) log 3 ( x 3) 1
log 3 ( x 1)( x 3) 1
log 3 ( x 1)( x 3) log 3 3
( x 1)( x 3) 3
x 2 3x x 3 3
x 4x 3 3 0
2
x2 4x 0
Пояснения и применяемые
формулы:
log a x log a y log a ( x y )
log a a 1
Левая и правая часть уравнения приведена к
логарифму по одному основанию
Раскроем скобки
Приведём подобные
Перенесём все слагаемые в лево
Решим неполное квадратное уравнение

8.

Решение логарифмического
уравнения по свойствам логарифма
Решение уравнения:
x2 4x 0
х ( х 4) 0
х 0или
х 4 0, х 4
х 0
log 3 (0 1) log 3 (0 3) 1
log 3 1 log 3 3 1
0 1 1,1 1
х 4
log 3 ( 4 1) log( 3)
Ответ: х = 0
Пояснения и применяемые
формулы:
Вынесем за скобки общий
множитель
Произведение равно нулю, когда хотя
бы один из множителей равен нулю
Сделаем проверку
log a 1 0, log a a 1
Верно
Посторонний корень
Не существует логарифма от
отрицательного числа.

9.

Решение логарифмического
уравнения по свойствам логарифма
6. Решите уравнение:
lg( x 2 2 х 7) lg( x 1) 0
Решение уравнения:
lg( x 2 2 х 7) lg( x 1) 0
x2 2x 7
lg
0
x 1
x2 2x 7
lg
lg 1
x 1
x2 2x 7
1
x 1
x2 2x 7 x 1
x2 2x 7 x 1 0
х2 х 6 0
Пояснения и применяемые
формулы:
log a x log a y log a
log a 1 0
Левая и правая часть уравнения
приведена к логарифму по одному
основанию
Применим свойство пропорции
Перенесём все слагаемые влево
Приведём подобные
Решим квадратное уравнение
x
y

10.

Решение логарифмического
уравнения по свойствам логарифма
Решение уравнения:
x2 x 6 0
a = 1, b = 1, c = -6
D 12 4 1 ( 6) 1 24 25
1 5
2 1
1 5
x2
2 1
x1
х 2
Пояснения и применяемые
формулы:
6
3
2
4
2
2
D b 2 4ac
x1, 2
b D
2a
Сделаем проверку
lg( 2 2 2 2 7) lg( 2 1) 0
lg 1 lg 1 0,0 0
х 3
lg( 3 1) lg( 4)
Ответ: х = 2
Верно
Посторонний корень
Не существует логарифма от
отрицательного числа.

11.

Решение логарифмического уравнения
введением новой переменной
7. Решите уравнение:
log 32 log 3 x 2 0
Решение уравнения:
log 32 log 3 x 2 0
t2 t 2 0
D ( 1) 4 1 ( 2) 1 8 9
2
1 3 2
1
2 1
2
1 3 4
t 2
2
2 1
2
t1
log 3 х 1
log 3 х 2
log 3 x log 3 3 1 log x log 32
3
3
1
1
x 3
x 32 9
3
Ответ: х1 = 1/3, х2 = 9.
Пояснения и применяемые
формулы:
Обозначим:
log 3 x t
Решим квадратное уравнение
D b 2 4ac
t1, 2
b D
2a
log a a b
b
Левая и правая часть уравнения
приведена к логарифму по одному
основанию

12.

Решите уравнения:
1.4 log4 ( x 7 ) 11
2. log 3 (5 x 1) 2
3. log 5 ( x 1) log( x 2) log( x 2)
4. log 22 x 3 log 2 x 4 0
5. log 2 x log 1 x 4
2
1.2 log2 ( x 15) 4
2. log 4 (5 2 x ) 3
3. lg 2 x lg x 6 0
4. log 23 ( 2 x 1) log 23 x 0
5. log 16 x log 4 x log 2 x 7

13.

Гимнастика для глаз
Сильно зажмурьте глаза, откройте глаза и посмотрите
на предмет перед Вами (повторите 5 раз).
Закройте глаза, откройте глаза, посмотрите направо,
посмотрите налево (повторите 5 раз).
Сильно зажмурьте глаза, откройте глаза и посмотрите
на предмет вдали от вас (повторите 5 раз).

14.

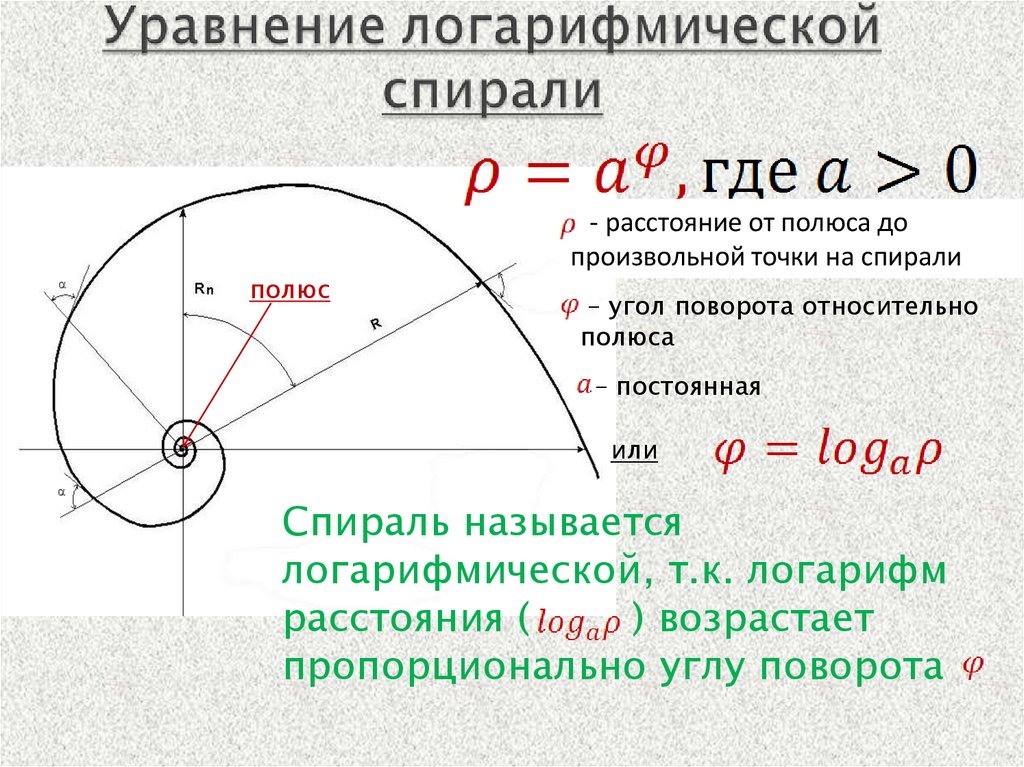
Логарифмическая спираль

15.

полюс
- расстояние от полюса до
произвольной точки на спирали
– угол поворота относительно
полюса
– постоянная
или
Спираль называется
логарифмической, т.к. логарифм
расстояния (
) возрастает
пропорционально углу поворота

16.

Если вращать спираль
вокруг полюса по
часовой стрелке, то
можно наблюдать
кажущееся растяжение
спирали.

17.

Если вращать спираль
вокруг полюса против
часовой стрелки, то
можно наблюдать
кажущееся сжатие
спирали.

18.

Спирали широко проявляют себя в
живой природе. Спирально
закручиваются усики растений, по
спирали происходит рост тканей в
стволах деревьев.

19.

В подсолнухе
семечки расположены
по дугам, близким к
логарифмической
спирали

20.

Рога животных растут
лишь с одного конца.
Этот рост осуществляется
по логарифмической
спирали. Например, рога
баранов, коз, антилоп и
других рогатых
животных.

21.

Раковины морских животных могут расти лишь в одном
направлении. Чтобы не слишком вытягиваться в длину,
им приходится скручиваться, причем каждый следующий
виток подобен предыдущему. Поэтому раковины многих
моллюсков, улиток, закручены по логарифмической
спирали.

22.

По логарифмической спирали
формируется тело циклона

23.

По логарифмическим спиралям закручены и
многие галактики, в частности – Галактика
Солнечной системы.

24.

Всем спасибо
за работу на уроке!
Удачи
в освоении
математики