Система параллельных сил и пар. Сложение параллельных сил

1.

P1 P2
3. СИСТЕМА ПАРАЛЛЕЛЬНЫХ СИЛ И ПАР
3.1. Сложение параллельных
сил
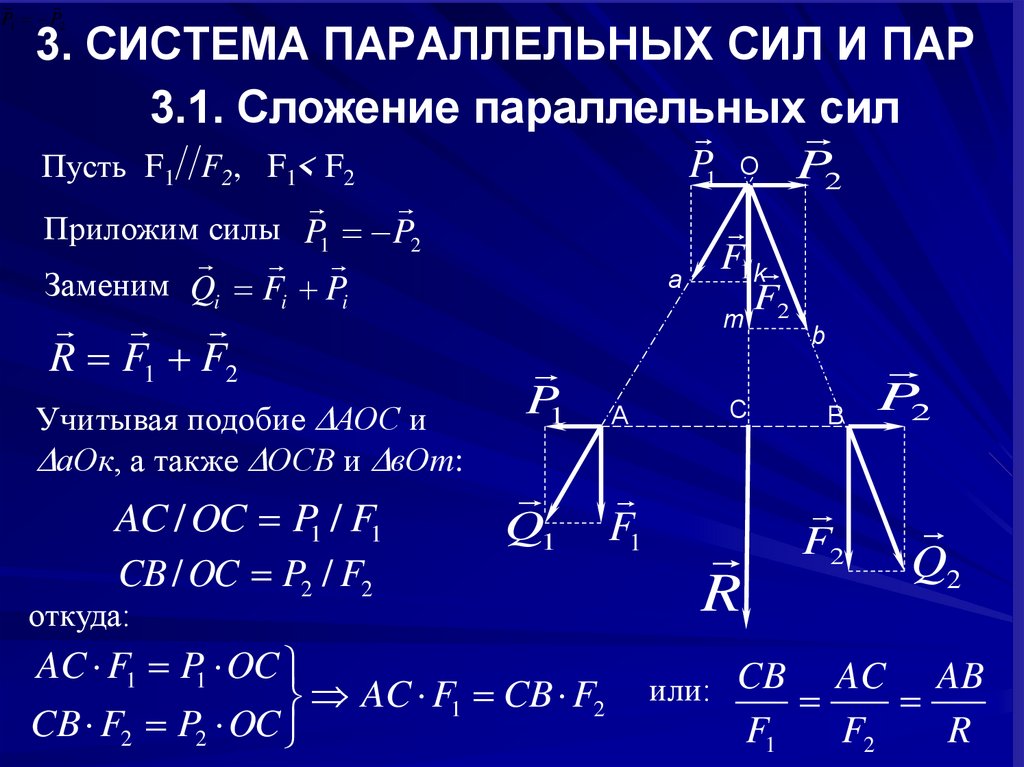
Пусть F1 F2, F1< F2
Приложим силы P1 P2
P1 O P2
Заменим Qi Fi Pi
R F1 F2
Учитывая подобие АОС и
аОк, а также ОСВ и вОm:
AC / OC P1 / F1
CB / OC P2 / F2
a
F1 k
F2
m
P1
A
Q1
F1
откуда:
AC F1 P1 OC
AC F1 CB F2
CB F2 P2 OC
b
C
B
F2
R
P2
Q2
или: CB AC AB
F1
F2
R

2.

Сложение двух сил, направленных в одну сторону
равнодействующая двух параллельных и направленных в одну
сторону сил, действующих на АТТ, равна по модулю сумме
модулей слагаемых сил, им параллельна и направлена в ту же
сторону; линия действия равнодействующей проходит между
точками приложения слагаемых сил на расстояниях от этих
точек, обратно пропорциональных их модулям
Сложение двух сил, направленных в противоположные стороны
равнодействующая R двух параллельных, направленных в
разные стороны, сил равна по модулю разности модулей
слагаемых сил, им параллельна и направлена в сторону большей
силы; линия действия равнодействующей проходит вне
отрезка, соединяющего точки приложения слагаемых сил на
расстояниях от этих точек, обратно пропорциональных силам
F2
B
A
C
F1
R
R F1 F2
BC AB AC
F1
R
F2

3.

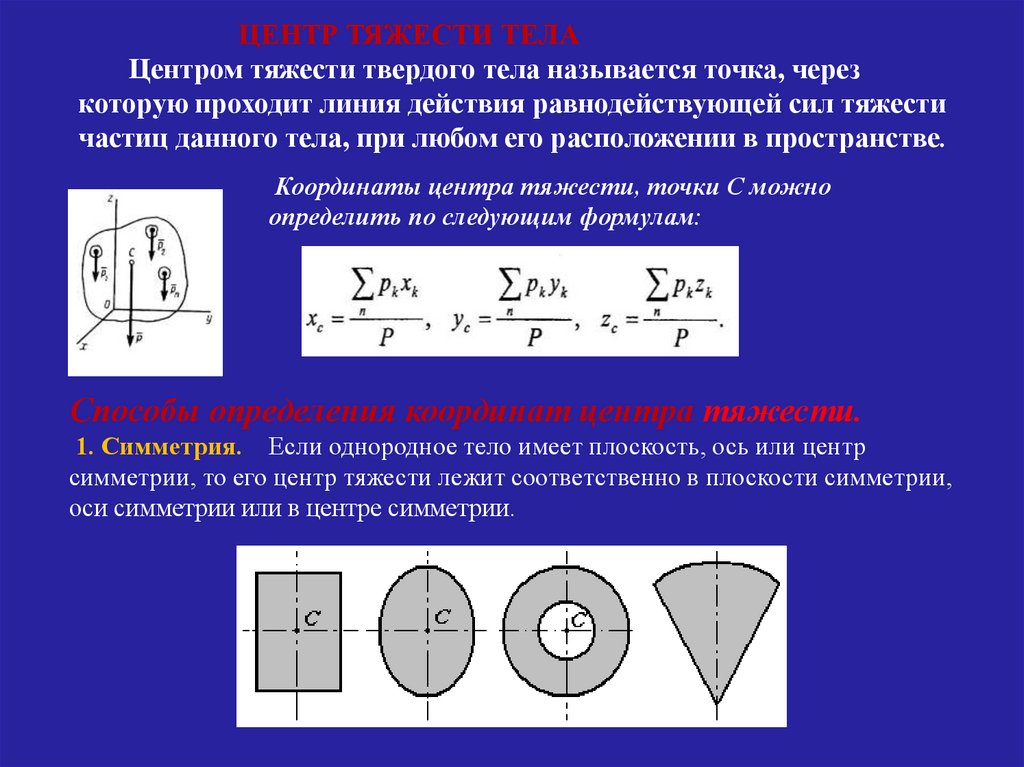
ЦЕНТР ТЯЖЕСТИ ТЕЛА
Центром тяжести твердого тела называется точка, через
которую проходит линия действия равнодействующей сил тяжести
частиц данного тела, при любом его расположении в пространстве.
Координаты центра тяжести, точки C можно
определить по следующим формулам:
Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр
симметрии, то его центр тяжести лежит соответственно в плоскости симметрии,
оси симметрии или в центре симметрии.

4.

2. Разбиение. Тело разбивается на конечное число частей, для каждой из которых
положение центра тяжести и площадь известны.
S=S1+S2
3. Метод отрицательных площадей. Частный случай способа разбиения. Он
применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и
вырезанной части известны. Тело в виде пластинки с вырезом представляют
комбинацией сплошной пластинки (без выреза) с площадью S1 и площади
вырезанной части S2 .

5.

Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести
треугольника лежит в точке пересечения его медиан.
Координаты центра тяжести треугольника представляют
собой среднее арифметическое из координат его
вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
2. Центр тяжести прямоугольника. Центр тяжести
прямоугольника лежит в точке пересечения его
диагоналей . Координаты центра тяжести
прямоугольника рассчитываются по
формулам: xc =b/2 ; yc =h/2.
3. Центр тяжести полукруга. Центр тяжести
полукруга лежит на оси симметрии. Координаты
центра тяжести полукруга рассчитываются по
формулам: xc =D/2 ; yc =4R/3π.