Similar presentations:
Расчет переходных процессов в электрических цепях операторным методом. Переход от изображений к оригиналам
1.
1Лекция 13
Расчет переходных процессов
в электрических цепях операторным методом.
Переход от изображений к оригиналам.
Формула разложения
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
2.
2Структуры записи операторного сопротивления
ветви и комплексного сопротивления этой же
ветви
1
Z k rk j Lk
j Ck
1
1
j
Ck j Ck
тождественны, и выражение для операторного
сопротивления Zk(p) можно получить через
комплексное сопротивление Zk путем замены
jω на p.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
3.
3Сопоставляя выражения законов Кирхгофа в
операторной форме с их выражением в
комплексной форме:
Ik 0
и
Ek I k Z k ,
мы видим, что при нулевых начальных условиях
законы Кирхгофа в операторной форме
одинаковы по виду с этими законами в
комплексной форме.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
4.
4Поэтому при нулевых начальных условиях
методы расчета любых сложных цепей при
переходных процессах операторным методом
аналогичны методам расчета установившихся
режимов комплексным методом.
При нулевых начальных условиях входное
операторное сопротивление сколь угодно
сложного пассивного двухполюсника можно
получить из комплексного сопротивления этого
двухполюсника заменой jω на p.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
5.
5Пример 1. При включении цепи r, С на
постоянное напряжение при uC(0+) = 0 имеем
r
U
U p
1
U
I ( p)
.
1
1
r
r
p
pC
rC
C Пользуясь изображением
функции e
t
1
,
p
U
можно записать i (t )
e
r
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
1
t
rC
.
Тэттэр А.Ю., Пономарев А.В.
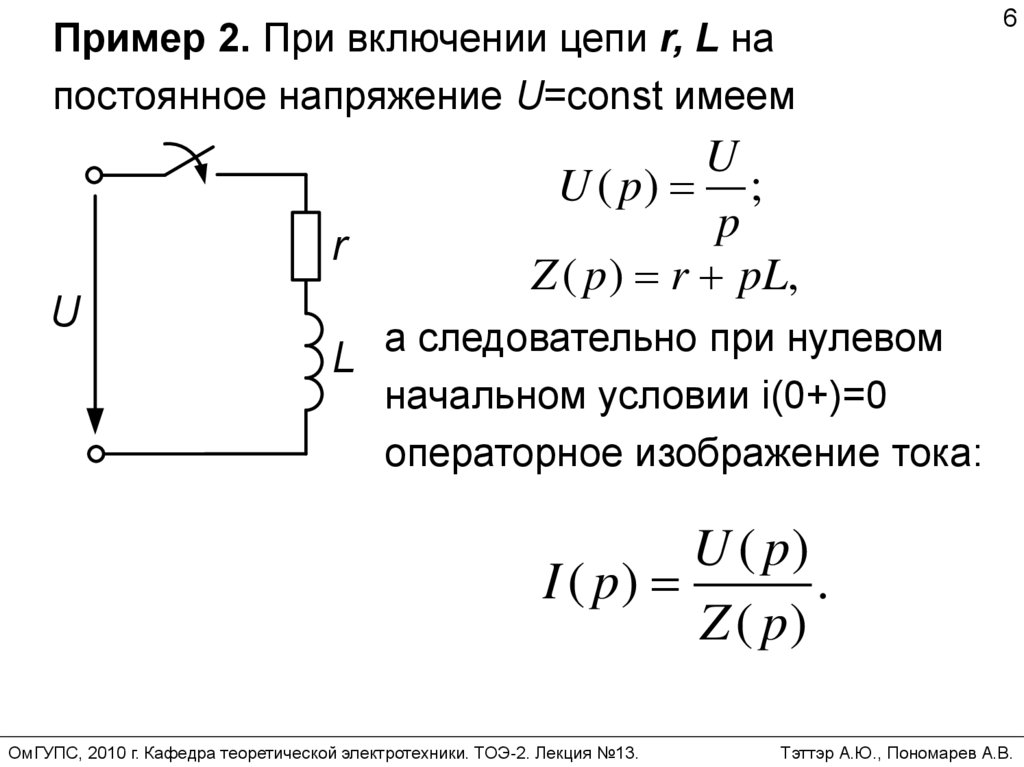
6.
Пример 2. При включении цепи r, L напостоянное напряжение U=const имеем
r
U
6
U
U ( p) ;
p
Z ( p ) r pL,
а следовательно при нулевом
L
начальном условии i(0+)=0
операторное изображение тока:
U ( p)
I ( p)
.
Z ( p)
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
7.
U ( p)U p
U
1
I ( p)
L
Z ( p ) r pL r
p 1 p
r
7
L
1 p 1
U 1 1
1
U 1
r
L r p
L
r p p
p 1 p
p 1 p
r
r
U 1
1
.
r p r p
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
8.
8Пользуясь изображениями функций
A
A
p
и
e
t
1
,
p
можно записать для искомого тока:
U
i (t ) 1 e
r
r
t
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
.
Тэттэр А.Ю., Пономарев А.В.
9.
9Достоинство операторного метода для расчета
переходных процессов, заключающееся в
алгебраизации дифференциальных уравнений
цепи, особенно проявляется при расчете
сложных цепей.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
10.
Обратное преобразование10
(переход от изображений к оригиналам)
При решении задач электротехники используют:
1. Обратное преобразование Лапласа:
f (t )
1
0 j
F ( p)e dp,
pt
2 j 0 j
где p 0 j .
2. Таблицы соответствия оригиналов и
изображений (приводятся в справочниках);
3. Формулу разложения.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
11.
11При расчете переходных процессов изображение
можно представить в виде рациональной дроби,
представляющей собой отношение двух
полиномов параметра p:
m 1
M ( p ) a0 p a1 p ... am
X ( p)
. (159)
n
n 1
N ( p)
b0 p b1 p ... bn
m
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
12.
12Переход от изображения X(p) к функции времени
(оригиналу) x(t), т.е. обратное преобразование,
осуществляется с помощью формулы
разложения.
В случае простых (некратных) корней
знаменателя выражение (159) можно
представить в виде суммы простых дробей, для
которых известны оригиналы:
M ( p)
A1
A2
An
...
, (*)
N ( p) p p1 p p2
p pn
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
13.
где A1, А2 … Аn – неизвестные покакоэффициенты;
p1, p2 … pn – корни знаменателя, т.е.
корни уравнения N(p)=0.
13
Умножим левую и правую части (*) на (p – p1) и
рассмотрим предел полученного выражения при
p p1
M ( p)( p p1 )
lim
p p1
N ( p)
A1 p p1
A2 p p1
An p p1
lim
lim
... lim
.
p p1
p p1
p p1
p p1
p p2
p pn
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
14.
0Предел левой части – неопределенность .
0
14
Применяем правило Лопиталя
M ( p)( p p1 ) M ( p) M ( p1 )
lim
.
p p1
N ( p)
N ( p1 )
В правой части остается A1.
M ( p1 )
M ( p2 )
A1
; A2
;
N ( p1 )
N ( p2 )
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
M ( pn )
An
.
N ( pn )
Тэттэр А.Ю., Пономарев А.В.
15.
Порядок расчета переходных процессовоператорным методом
15
1. Расчет установившегося режима
до коммутации. Определение iL(0–), uC(0–).
2. Формирование уравнения для нахождения
изображения. Два способа.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
16.
16а) Составление дифференциальных
уравнений для послекоммутационного
состояния цепи для мгновенных значений
токов и напряжений.
Переход к алгебраическим уравнениям для
изображений с помощью преобразования
Лапласа.
б) Составление операторной схемы
замещения и запись для нее операторных
уравнений.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
17.
Порядок расчета переходных процессовоператорным методом
17
1. Расчет установившегося режима
до коммутации. Определение iL(0–), uC(0–).
2. Формирование уравнения для нахождения
изображения. Два способа.
3. Нахождение изображения искомого тока или
напряжения.
4. Переход от изображения I(p) или U(p) к
оригиналу i(t) или u(t) с помощью таблицы
соответствия или формулы разложения.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
18.
18Операторный метод расчета
переходных процессов
(примеры расчета)
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №13.
Тэттэр А.Ю., Пономарев А.В.
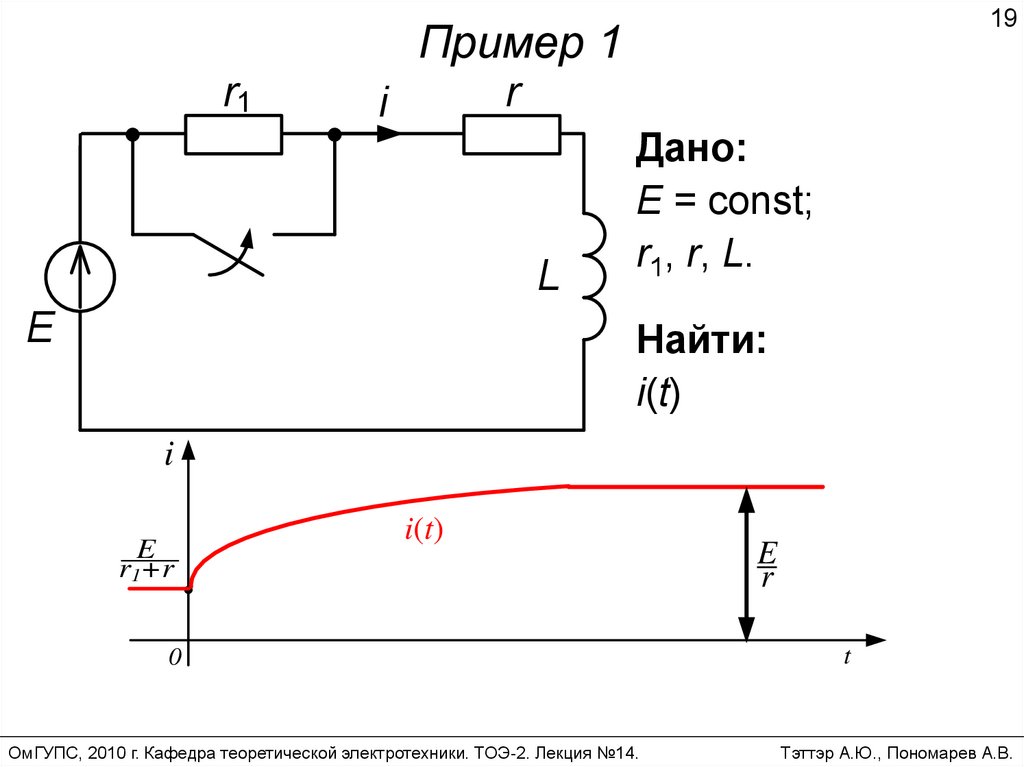
19.
19Пример 1
r1
r
i
L
E
Дано:
E = const;
r1, r, L.
Найти:
i(t)
i
E .
r1+r .
i(t)
0
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
E
r
t
Тэттэр А.Ю., Пономарев А.В.
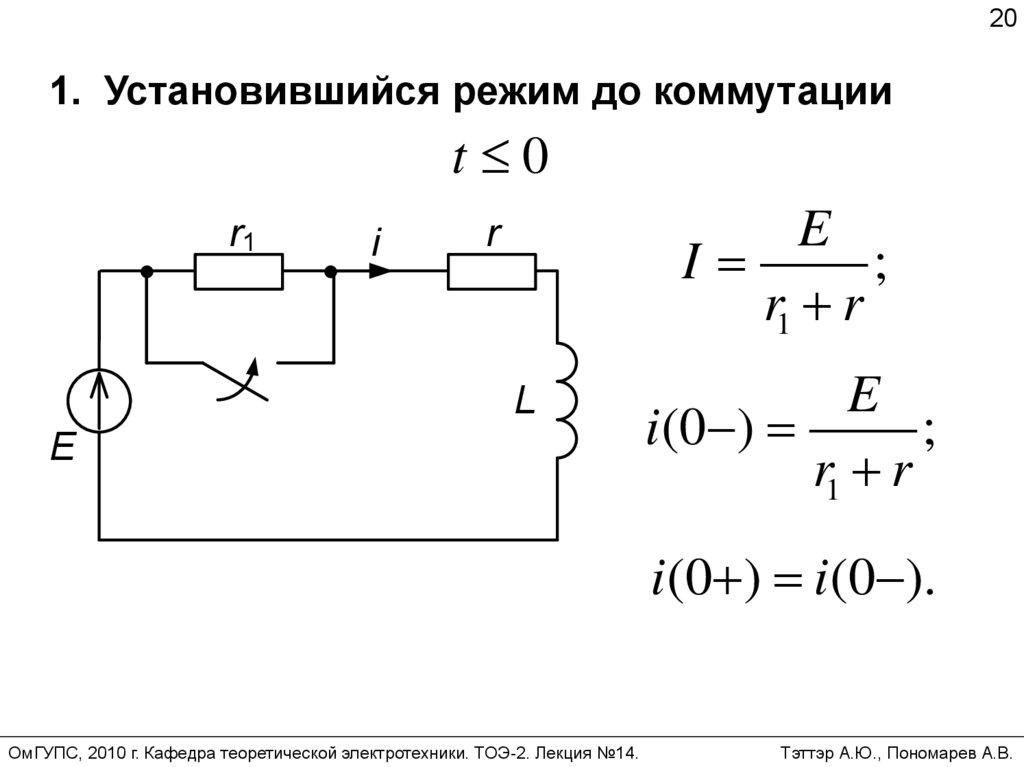
20.
201. Установившийся режим до коммутации
t 0
r1
i
E
I
;
r1 r
r
L
E
E
i (0 )
;
r1 r
i (0 ) i(0 ).
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
21.
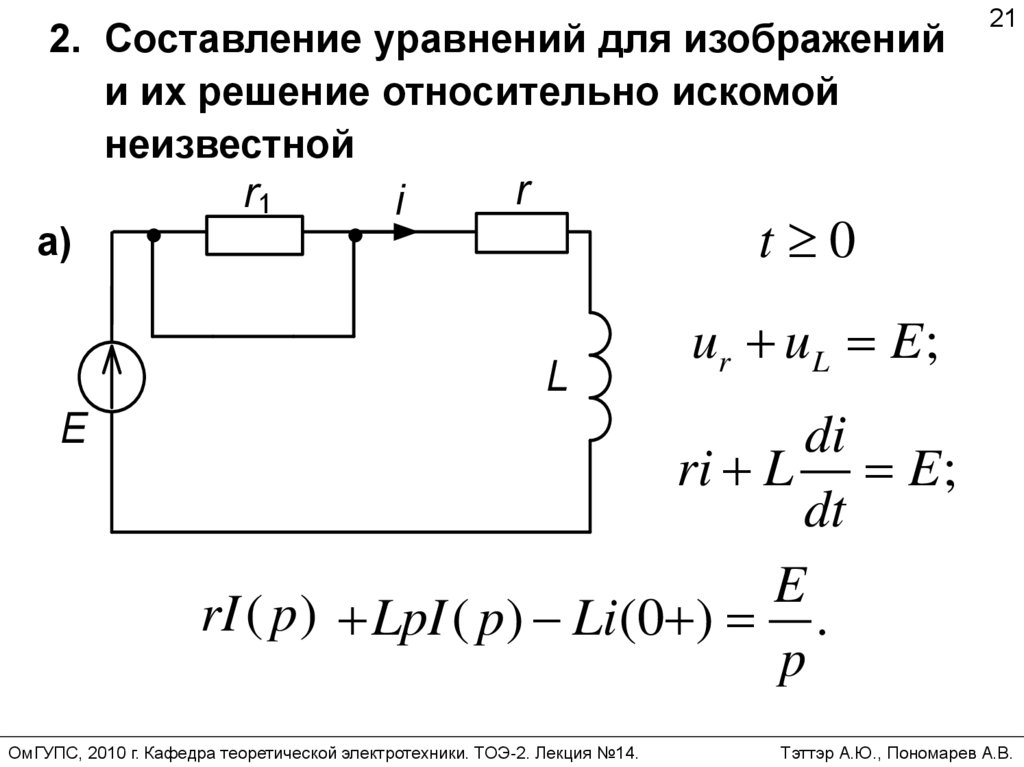
2. Составление уравнений для изображенийи их решение относительно искомой
неизвестной
r1
i
r
t 0
a)
L
E
21
ur u L E ;
di
ri L E;
dt
E
rI ( p) LpI ( p) Li (0 ) .
p
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
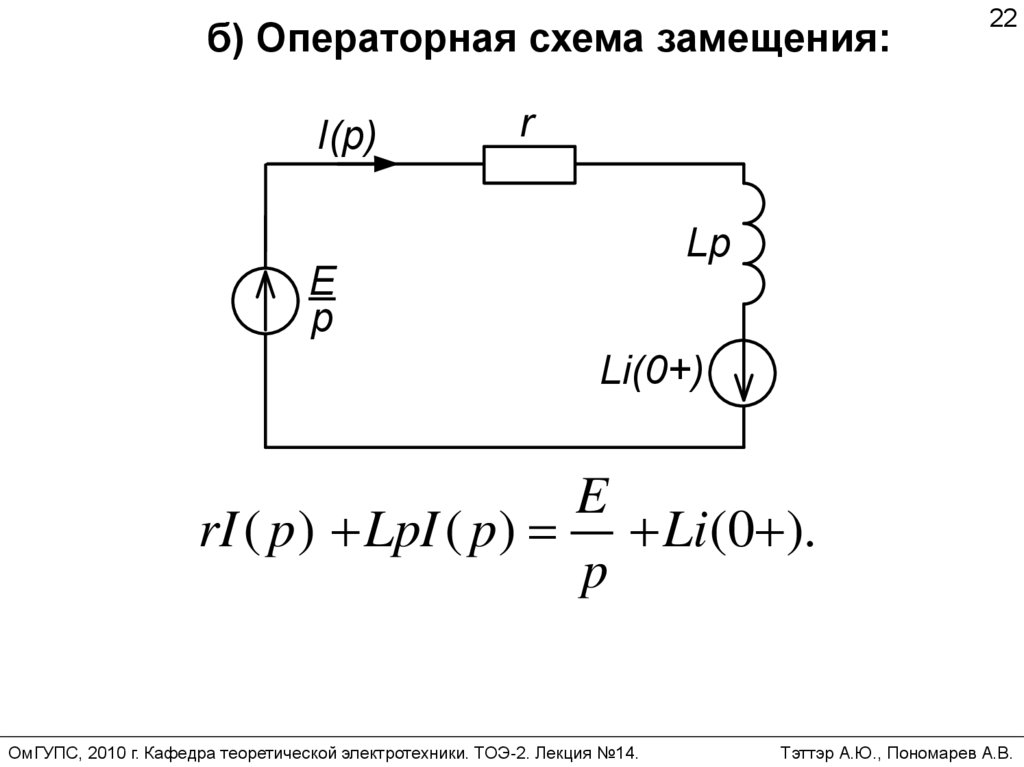
22.
б) Операторная схема замещения:I(p)
22
r
Lp
E
p
Li(0+)
E
rI ( p) LpI ( p) Li (0 ).
p
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
23.
3. Нахождение изображения искомойнеизвестной величины
23
E
rI ( p ) LpI ( p ) Li (0 );
p
E
Li (0 )
E Lpi (0 ) M ( p )
p
I ( p)
.
p r Lp
r Lp
N ( p)
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
24.
4. Нахождение оригинала i(t), поформуле разложения
24
M ( pk ) pk t
i (t )
e ;
N ( pk )
N ( p) 0;
p(r Lp) 0;
p1 0;
r
p2 .
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
25.
M ( p) E Lpi (0 );25
M ( p1 ) E ;
Er
r E
E
;
M ( p2 ) E L
r1 r
L r1 r
N ( p) r 2 Lp;
N ( p1 ) r ;
r
N ( p2 ) r 2 L r.
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.
26.
M ( p1 ) p1t M ( p2 ) p2ti (t )
e
e
N ( p1 )
N ( p2 )
r
E E
r
E
r r1 L t
e
r
r
E E
E
e
r r r1 r
E
i (0)
;
r1 r
r
t
L
26
;
E
i ( ) .
r
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №14.
Тэттэр А.Ю., Пономарев А.В.





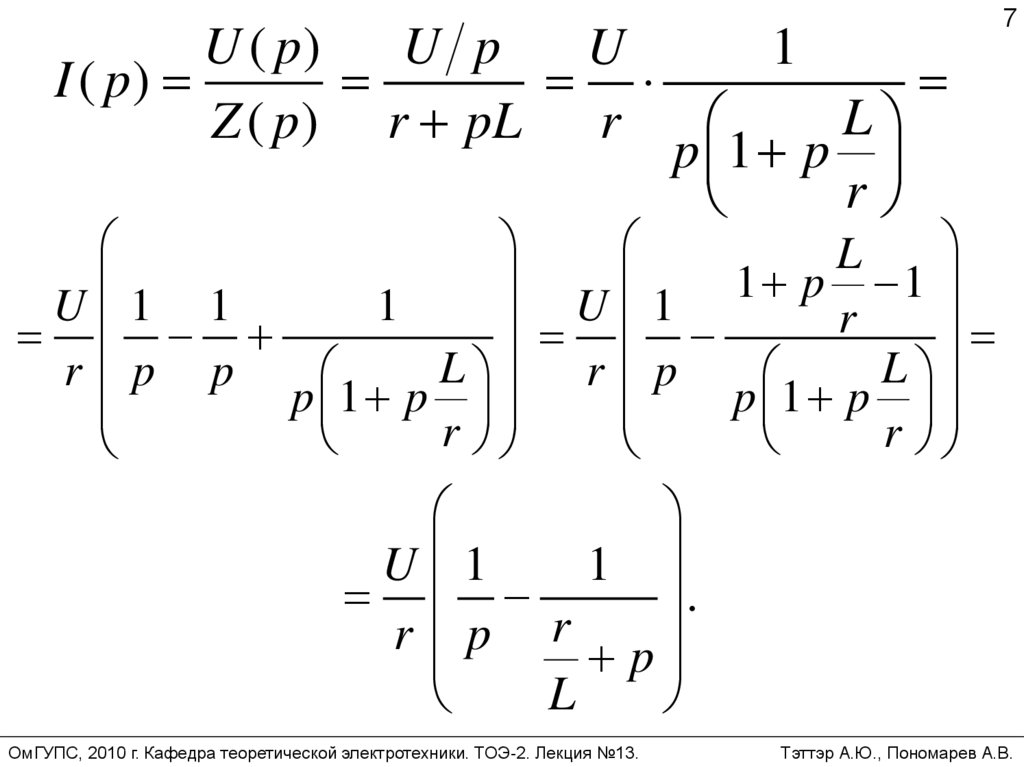













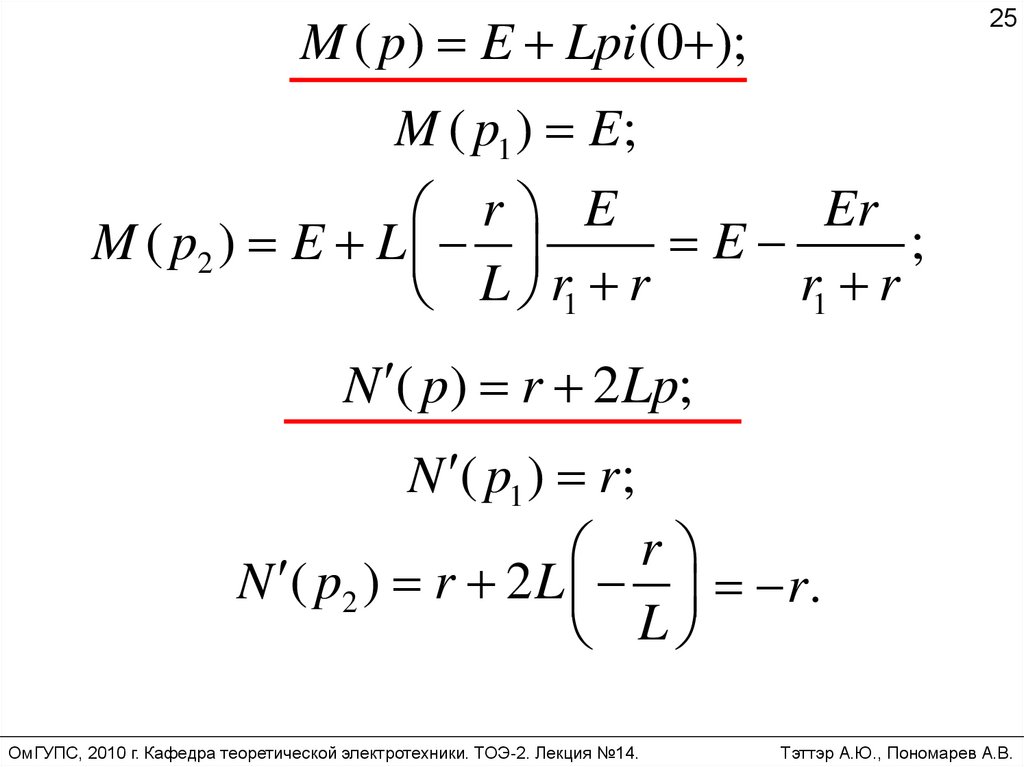
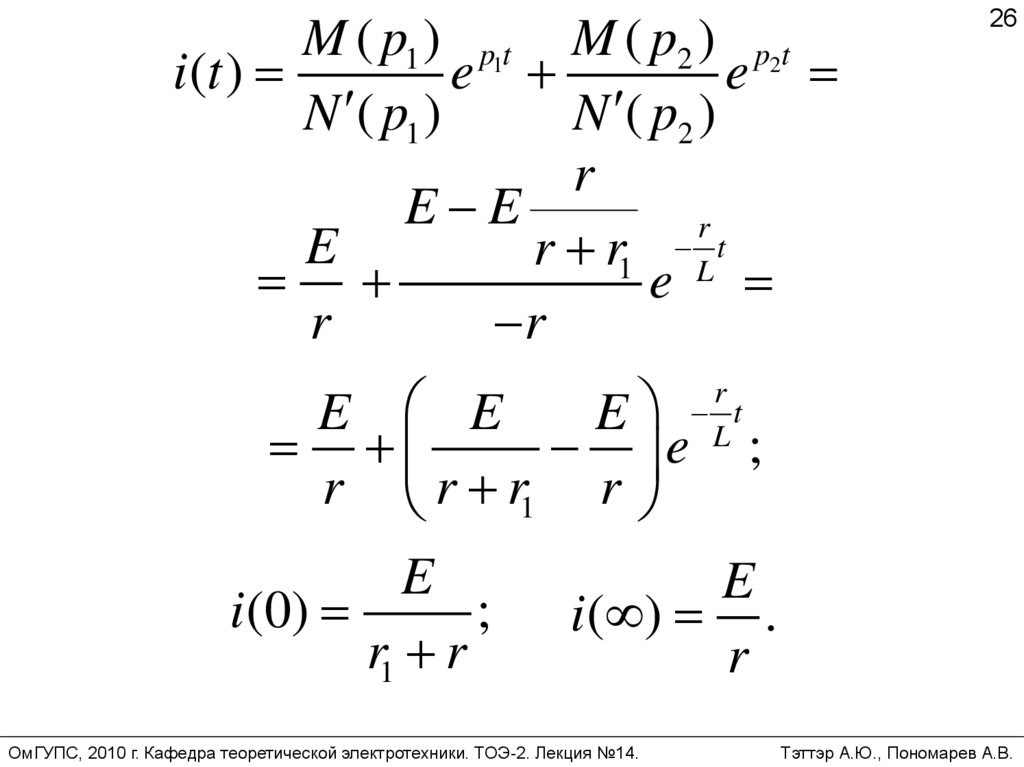
 physics
physics








