Теоретические основы электротехники

1.

Теоретические основы
электротехники
(часть 3)
Лекции: 30 часов
Лабораторные занятия: 16 часов
Практические занятия: 16 часов
Самостоятельная работа: 56 часов
Форма контроля: зачет с оценкой
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №1.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

2.

Рекомендуемая литература:
2
Четырехполюсники: Методические указания и задания для
самостоятельной работы студентов / А.Г. Зверев, А.А.
Рублева, А.Ю. Тэттэр, В.Ю. Тэттэр; Омский гос. ун-т путей
сообщения. Омск, 2009. 36 с.
Электрические цепи с распределенными параметрами:
Учебное пособие / А.А. Комяков, Н.В. Пашкова, А.В.
Пономарев, А.Ю. Тэттэр; Омский гос. ун-т путей сообщения.
Омск, 2011. 71 с.
Нелинейные электрические цепи: Методические указания
к лабораторным работам / М.М. Никифоров, А.А. Рублева,
А.Ю. Тэттэр; Омский гос. ун-т путей сообщения. Омск, 2007.
44 с.
Нелинейные цепи: Учебное пособие / Т.В. Ковалева, О.О.
Комякова, А.Ю. Тэттэр, А.Г. Зверев; Омский гос. ун-т путей
сообщения. Омск, 2011. 86 с.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №1.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

3.

Рекомендуемая литература:
3
Тэттэр А. Ю. Основы теории электрических цепей: Учебное
пособие / А.Ю. Тэттэр, А.В. Пономарев; Омский гос. ун-т путей
сообщения. Омск, 2012. 143 с.
Зажирко В. Н. Переходные процессы в линейных
электрических цепях: Учебное пособие / В.Н. Зажирко, А.Ю.
Тэттэр / Под ред. В.Н. Зажирко; Омский гос. ун-т путей
сообщения. Омск, 2006, 91 с.
СТП ОмГУПС-1.2-2005. Общие требования и правила
оформления текстовых документов/Омский гос. ун-т путей
сообщения. Омск, 2005. 29 с.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №1.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

4.

4
ЦЕПИ С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

5.

5
Лекция 1
Уравнение однородной линии.
Установившийся синусоидальный режим линии
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

6.

6
Особенности функционирования электрических
цепей с распределенными параметрами
зависят от распределения сопротивлений,
проводимостей, индуктивностей и емкостей
по длине линии.
Это различные воздушные и кабельные линии
из области энергетики, проводной связи,
радиотехники, передачи информации.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

7.

7
Протяженность линии оказывает существенное
влияние на протекание в ней электромагнитных
процессов из-за конечной скорости
распространения этих процессов.
Поэтому основные соотношения и уравнения
линий содержат две независимые переменные –
время и пространственную координату.
Рассмотрим модель двухпроводной линии
как простейшего представителя
рассматриваемого класса цепей.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

8.

8
Из-за распределенного характера параметров
линий электромагнитные процессы в них носят
волновой характер.
Математическое описание этих процессов
строится на использовании понятий прямых и
обратных волн напряжения и тока.
В отличие от цепей с сосредоточенными
параметрами законы Кирхгофа не могут быть
записаны для линии в целом.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

9.

9
Для обозначения цепей с распределенными
параметрами часто используется термин
«длинная линия».
В основу этого понятия положено условие
соизмеримости протяженности линии с длиной
волны синусоидального напряжения (тока).
Однако, при рассмотрении более широкого
спектра вопросов следует использовать понятие
«цепь с распределенными параметрами».
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

10.

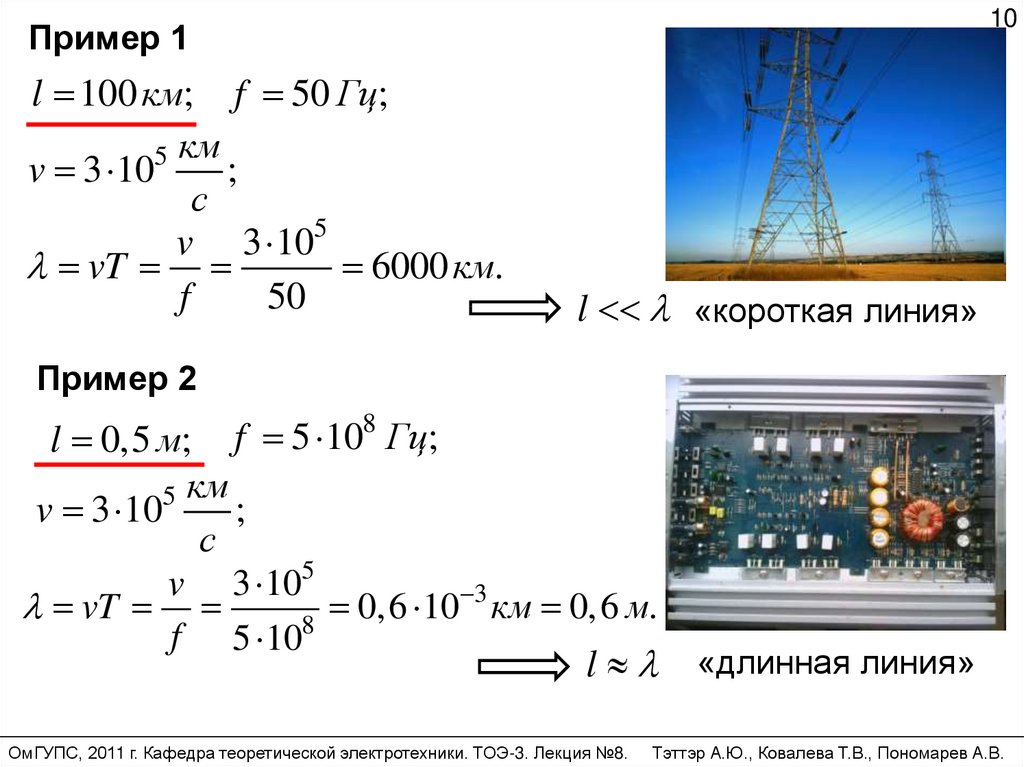
10
Пример 1
l 100 км; f 50 Гц;
5 км
v 3 10
;
с
v 3 105
vT
6000 км.
f
50
l «короткая линия»
Пример 2
f 5 108 Гц;
l 0,5 м;
5 км
v 3 10
;
с
v 3 105
3
vT
0,6
10
км 0,6 м.
8
f 5 10
l
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
«длинная линия»
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

11.

11
Дифференциальные уравнения
однородной двухпроводной линии
При математическом исследовании линий
используются первичные параметры,
задаваемые на единицу длины линии:
– сопротивление r0, Ом/км (Ом/м);
– индуктивность L0, Гн/км (Гн/м);
– емкость C0, Ф/км (Ф/м);
– проводимость g0, См/км (См/м).
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

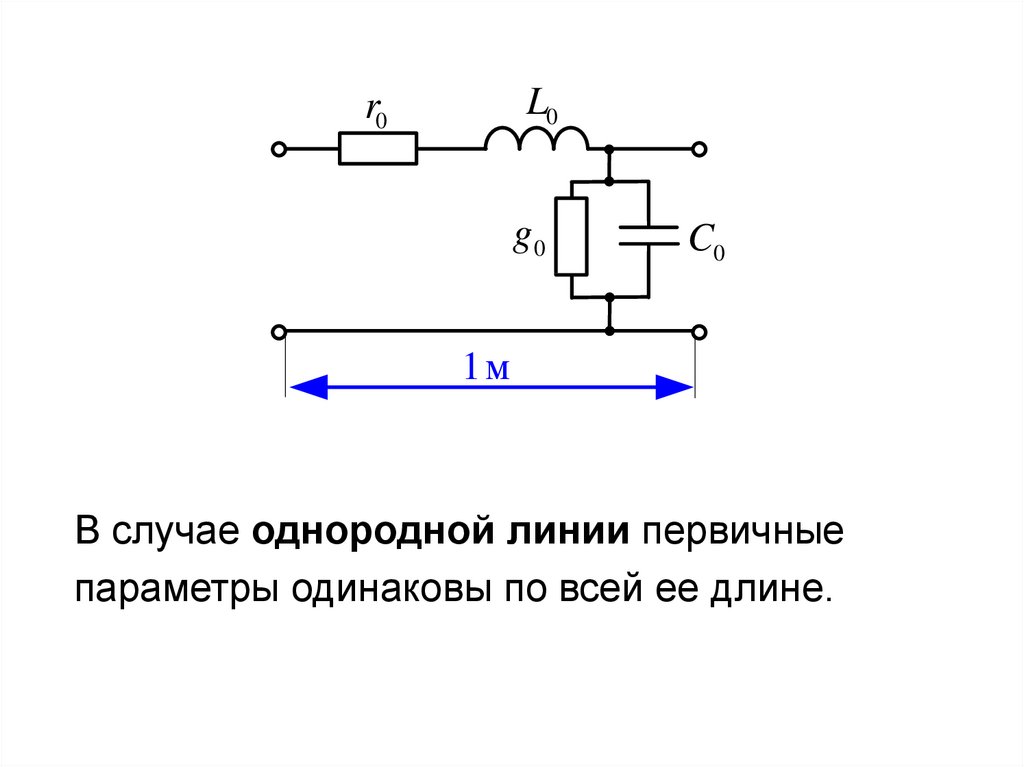
12.

L0
r0
g0
C0
1м
В случае однородной линии первичные
параметры одинаковы по всей ее длине.

13.

13
Сопротивление r0 и индуктивность L0
характеризуют провода линии и называются
продольными параметрами.
Емкость C0 и проводимость g0 относятся к среде,
окружающей провода, и называются
поперечными параметрами.
Проводимость среды и распределенная емкость
между проводами обусловливают токи утечки
через изоляцию по всей длине линии.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

14.

14
iвх
iн
i1
i2
in-1
in
uн
uвх
Ток нагрузки iН из-за токов утечки не равен ее
входному току iВХ.
Кроме того, фазы напряжений и токов
изменяются вдоль линии, что также требуется
учитывать в расчетах.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

15.

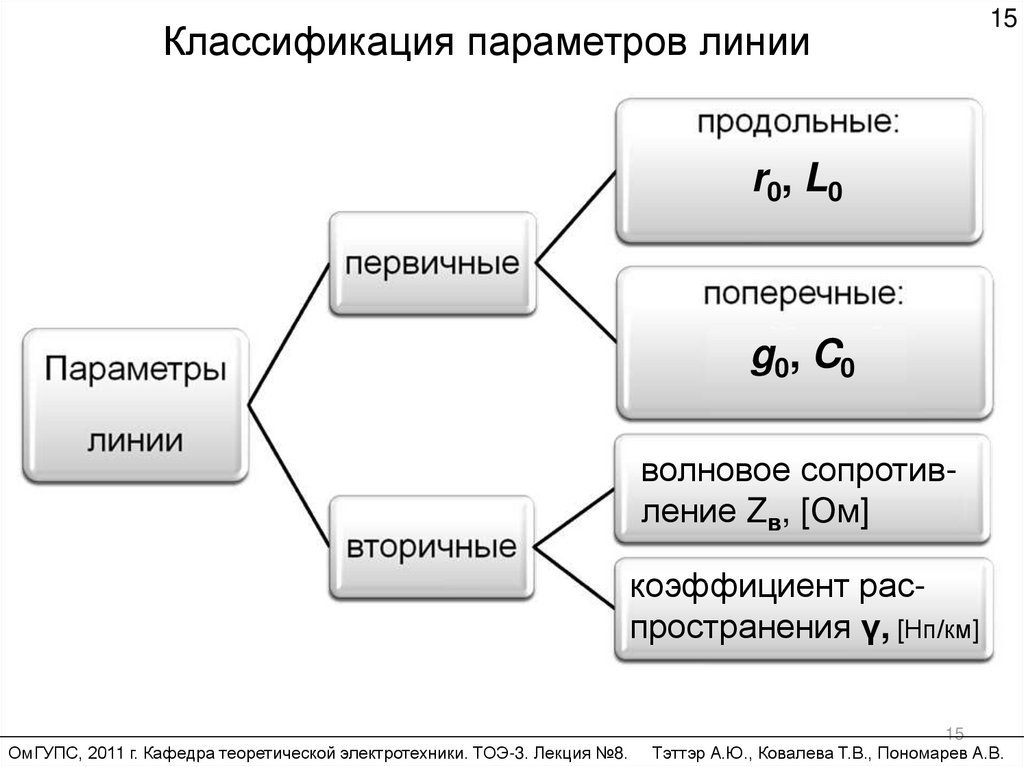
Классификация параметров линии
15
r0, L0
g0, C0
волновое сопротивление Zв, [Ом]
коэффициент распространения γ, [Нп/км]
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
15
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

16.

Схема замещения линии
(цепная или цепочечная схема)
16
Для получения дифференциальных уравнений
линию представляют как набор малых элементов,
для каждого из которых записываются законы
Кирхгофа.
Полученный результат распространяют на всю
линию.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

17.

Рассмотрим бесконечно малый элемент линии с
распределенными параметрами:
i
i dx
L0 dx
x
r0 dx
i
ig
iC
u
C0 dx
g 0 dx
u
dx
u
x
x
С учетом равенств
17
dx
duC
ig gu g , iC C
dt
для контура и узла этой цепи можно записать:
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

18.

r0 dx
i
L0 dx
ig
i
i dx
x
iC
g 0 dx
u
x
C0 dx
u
18
u
dx
x
dx
i
u
dx
u u dx L0 dx r0 dx i 0;
t
x
u
i
i dx g 0 dx u dx
dx
x
x
u
C0 dx u dx i 0.
t
x
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

19.

19
i
u
r
i
L
;
0
0
x
t
i
u
u
u
g 0u C0
g0
dx C0 ( dx ) .
t x
t x
x
Составляющие в квадратных скобках
представляют собой величины второго порядка
малости, которыми можно пренебречь.
В результате приходим к системе двух
дифференциальных уравнений с частными
производными:
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

20.

i
u
x r0i L0 t ;
i
u
g 0u C0 ,
x
t
20
(1)
которые в литературе получили название
телеграфных уравнений.
Здесь независимыми переменными являются
время t и пространственная координата x,
совпадающая с направлением линии.
Эти уравнения, а также уравнения, выводимые на
их основе, применимы к различным видам линий.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

21.

21
a
б
в
г
а – двухпроводная воздушная линия;
б – коаксиальный кабель;
в – трехфазная линия;
г – двухжильный симметричный кабель.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

22.

Установившийся
синусоидальный режим линии
22
В этом случае решение дифференциальных
уравнений проводится для комплексов
напряжения и тока
U ( x)
и
I ( x).
Так как комплексные величины не являются
функциями времени, то задача сводится к
решению системы обыкновенных
дифференциальных уравнений с постоянными
коэффициентами.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

23.

Подставим
U ( x)
и
I ( x)
23
в (1):
dU ( x)
dx (r0 j L0 ) I ( x);
dI ( x) ( g j C )U ( x);
0
0
dx
(2)
d U ( x)
dI ( x)
dx 2 (r0 j L0 ) dx ;
2
d I ( x) ( g j C ) dU ( x) .
0
0
2
dx
dx
2
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

24.

24
Получаем уравнения Гельмгольца:
d U ( x)
2
dx 2 U ( x) 0;
2
d I ( x) 2 I ( x) 0,
dx 2
2
где
(3)
(r0 j L0 )( g 0 j C0 ) j
комплексное число, называемое
коэффициентом распространения.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

25.

Каждому из уравнений (3) соответствует
характеристическое уравнение
p 0,
2
имеющее корни
25
2
p1 ;
p2 .
Для напряжения
U ( x) решение имеет вид:
U ( x) U пр U св ; U пр U ( x) 0;
U св A1e
p1 x
U ( x) A1e
A2e
x
x
p2 x
,
x
A2e ,
где A1 и A2 – неизвестные постоянные.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

26.

26
Решение для тока можно получить из первого
уравнения системы (2):
dU ( x)
(r0 j L0 ) I ( x);
dx
( A1e
x
x
A2e ) (r0 j L0 ) I ( x),
откуда
I ( x)
r0 j L0
r0 j L0
( A1e
x
x
A2e );
r0 j L0 g0 j C0
r0 j L0
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

27.

Запишем решение для тока в виде
27
1
x
x
I ( x)
( A1e A2e ),
Zв
где
Zв
r0 j L0
g 0 j C0
– комплексное число,
называемое волновым
сопротивлением.
В итоге можно записать систему уравнений
U ( x) A1e x A2e x ;
1
x
x
I ( x) Z ( A1e A2e ).
в
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
(4)
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

28.

28
Определение А1 и А2 осуществляется по
граничным значениям напряжения и тока
(при x = 0 или x = ℓ ), где ℓ - длина линии.
Условимся обозначать через U1 и I1 комплексы
напряжения и тока в начале линии, а через
U 2 и I 2 – в конце линии.
Если заданы U1 и I1 , то система (4)
записывается при x = 0:
U1 A1 A2 ;
1
I
(
A
A
).
1
1
2
Zв
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
+
–
Zв
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

29.

Решение этой системы дает значения постоянных:
29
1
1
A1 (U1 I1Z в ); A2 (U1 I1Z в ),
2
2
подстановка которых в (4) приводит к
соотношениям:
1
1
x
x
U
(
x
)
(
U
I
Z
)
e
(
U
I
Z
)
e
;
1
1
в
1
1
в
2
2
(5)
1
1
x
x
I ( x)
(U1 I1Z в )e
(U1 I1Z в )e .
2Zв
2Zв
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

30.

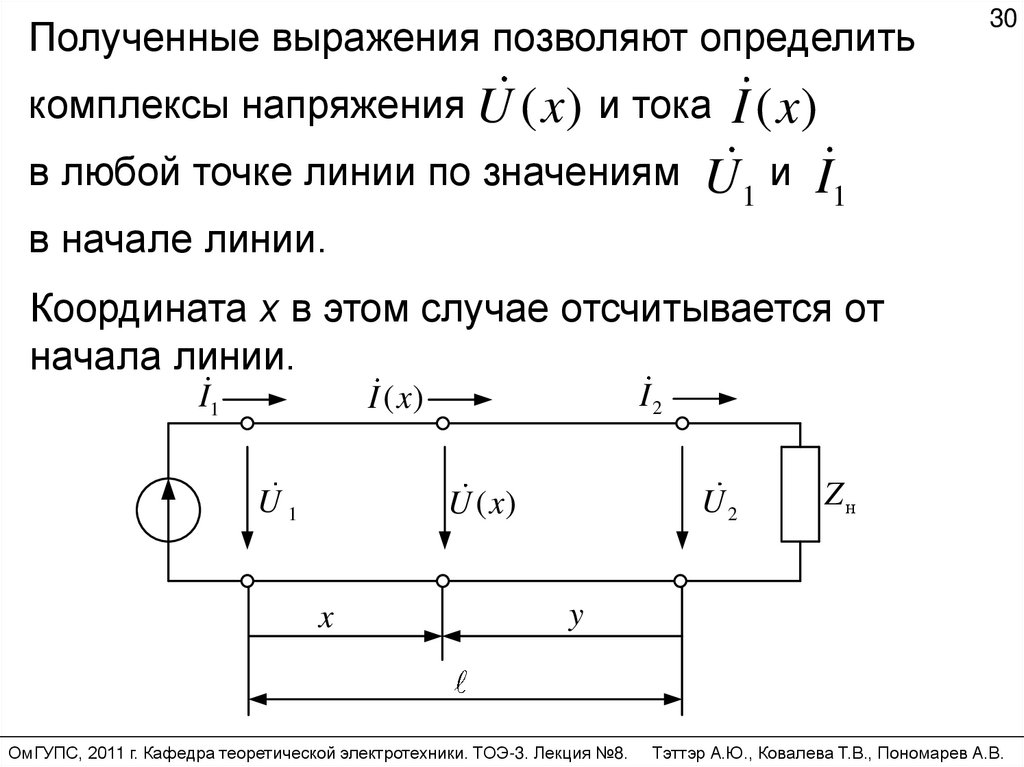
Полученные выражения позволяют определить
30
комплексы напряжения U ( x ) и тока
в любой точке линии по значениям
I ( x)
U1 и I1
в начале линии.
Координата х в этом случае отсчитывается от
начала линии.
I1
I2
I ( x)
U1
U2
U ( x)
x
Zн
y
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

31.

31
При известных U и I координата y
2
2
отсчитывается от конца линии.
Выразим А1 и А2 через напряжение и ток в конце
линии.
I1
x y;
I2
I ( x)
U1
U2
U ( x)
x
Zн
y
Граничные условия (при у = 0):
x ;
U U2;
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
I I2;
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

32.

32
При подстановке в (4) x = ℓ получим:
U 2 A1e A2e ;
Z в I 2 A1e A2e ;
U 2 Zв I 2 1
U
Z
I
e
;
A1
2
в
2
2
2e
U 2 Zв I 2 1
U
Z
I
e
;
A2
2
в
2
2
2e
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

33.

33
Полученные коэффициенты А1 и А2 подставляем
в (4), заменяя x на ℓ – y:
A1
x
1
U ( y ) (U 2 I 2 Z в )e e ( y ) A
2
2
x
1
( y )
(U 2 I 2 Z в )e e
;
2
1
( y )
I ( y)
(U 2 I 2 Z в )e e
2Zв
1
( y )
(U 2 I 2 Z в )e e
;
2Zв
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

34.

34
1
1
y
y
U
(
y
)
(
U
I
Z
)
e
(
U
I
Z
)
e
;
2
2
в
2
2
в
2
2
(6)
1
1
y
y
I ( y)
(U 2 I 2 Z в )e
(U 2 I 2 Z в )e .
2Zв
2Zв
Эти выражения позволяют определить
напряжение и ток в любой точке линии по
известным величинам U 2 и I 2 в конце линии.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

35.

35
Выражения (5) и (6) можно преобразовать с
учетом известных соотношений для
гиперболических функций:
1 a a
ch a (e e );
2
1 a a
sh a (e e ).
2
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

36.

При известных входных величинах
36
U1 и I1 :
U ( x) U1ch x I1Z вsh x;
U1
I ( x) I1ch x Z sh x.
в
При известных
U 2 и I2 :
U ( y ) U 2ch y I 2 Z вsh y;
U2
I ( y ) I 2ch y Z sh y.
в
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
(7)
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

37.

Из (7) при
y
U ( ) U1 , откуда
37
U1 AU 2 BI 2 ;
I1 CU 2 DI 2 ,
где
A ch ;
B Z вsh ;
1
C
sh ;
Zв
A D
D ch .
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

38.

Приведенные соотношения получены в
предположении, что линия является линейной
электрической цепью.
38
Для такой цепи применим принцип наложения,
поэтому указанные соотношения могут быть
использованы для расчета несинусоидальных
режимов, когда токи и напряжения содержат кроме
основной еще и высшие гармоники.
В этом случае расчет ведется отдельно для
каждой гармоники.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №8.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.