Similar presentations:
Переходные процессы в цепях с r и L, r и C при синусоидальных напряжениях и токах. Лекция 9
1.
1Лекция 9
Переходные процессы
в цепях с r и L, r и C
при синусоидальных напряжениях и токах
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
2.
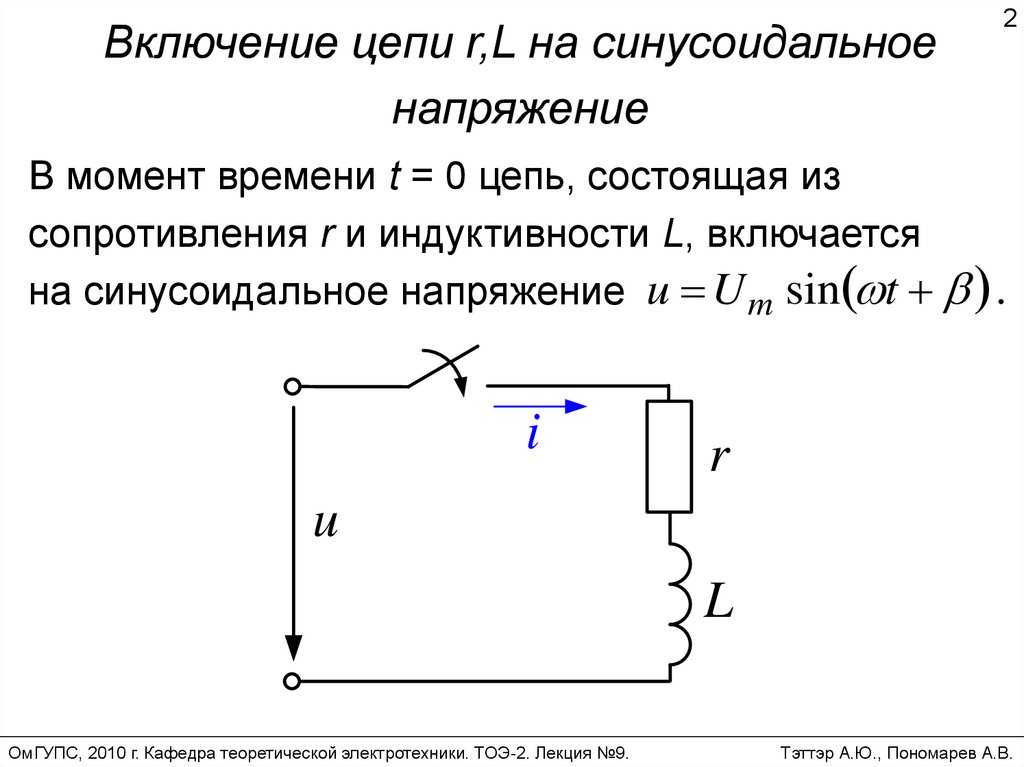
Включение цепи r,L на синусоидальноенапряжение
2
В момент времени t = 0 цепь, состоящая из
сопротивления r и индуктивности L, включается
на синусоидальное напряжение u U m sin t .
i
r
u
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
3.
Уравнение по второму закону Кирхгофа:или
3
ur u L u
di
r i L U m sin t .
dt
Характеристическое уравнение имеет вид:
r pL 0
и, соответственно, корень
r
p .
L
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
4.
4Переходный ток в цепи состоит из суммы
принужденного и свободного токов:
i iпр iсв .
Принужденная составляющая по форме
совпадает с формой приложенного напряжения.
Следовательно, принужденная составляющая
тока – синусоидальная функция времени и ее
удобнее всего рассчитывать комплексным
методом.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
5.
5U m U m e j
j
I
e
,
I m пр
m
пр
j
Z
ze
где Z = r + jωL
– комплексное сопротивление;
z r L
– модуль комплексного сопротивления;
2
arctg
2 2
L – аргумент комплексного сопротивления,
r
Um
Im пр
z
представляющий собой угол сдвига фаз
между напряжением u и током i;
– амплитуда тока.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
6.
Мгновенное значение принужденной составляющей6
iпр Jm I m пр e j t ;
iпр I m пр sin t I m пр sin t .
Свободная составляющая не зависит от
напряжения на входе цепи и записывается
так же, как в предыдущих задачах:
iсв Ае pt .
Решение для тока:
i (t ) I m пр sin t
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
r
t
Ae L .
Тэттэр А.Ю., Пономарев А.В.
7.
7Постоянная А определяется при t = 0+:
i 0 iпр 0 iсв 0 I m пр sin A.
Величина i(0+) находится на основании первого
правила коммутации:
i(0+) = i(0–) = 0,
так как до коммутации ток был равен нулю.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
8.
8Следовательно,
0 I m пр sin A,
откуда
A I m пр sin .
Ток в цепи
i I m пр sin t I m пр sin
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
r
t
e L.
Тэттэр А.Ю., Пономарев А.В.
9.
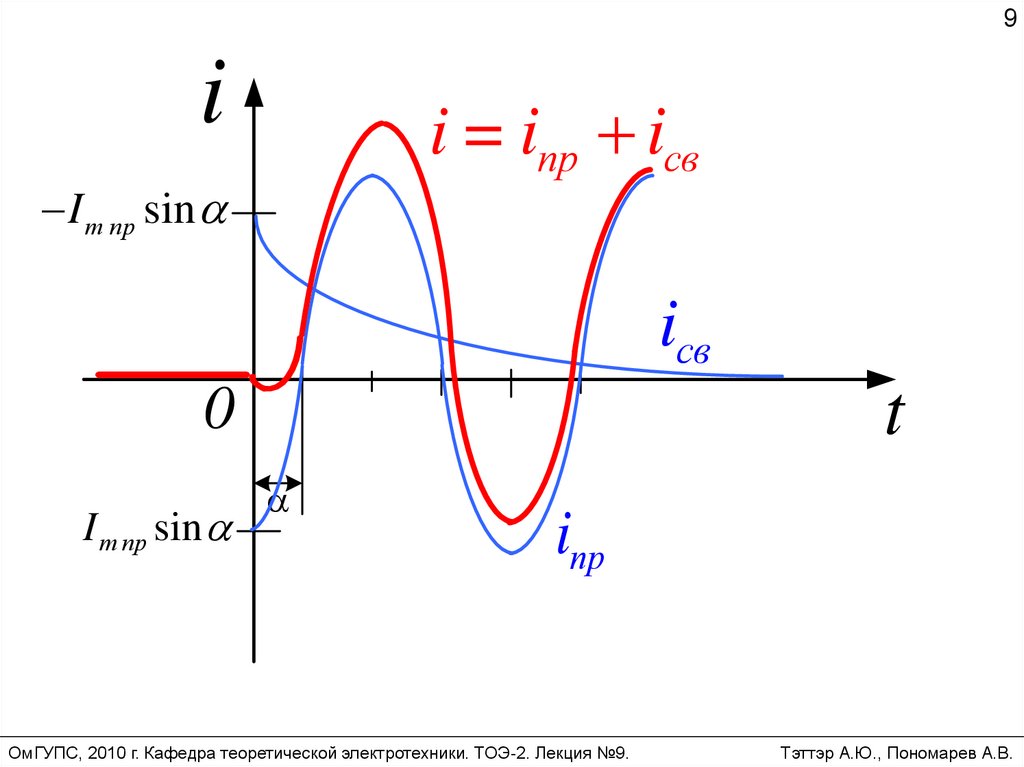
9i
i = iпр iсв
I m пр sin
iсв
t
0
I m пр sin
iпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
10.
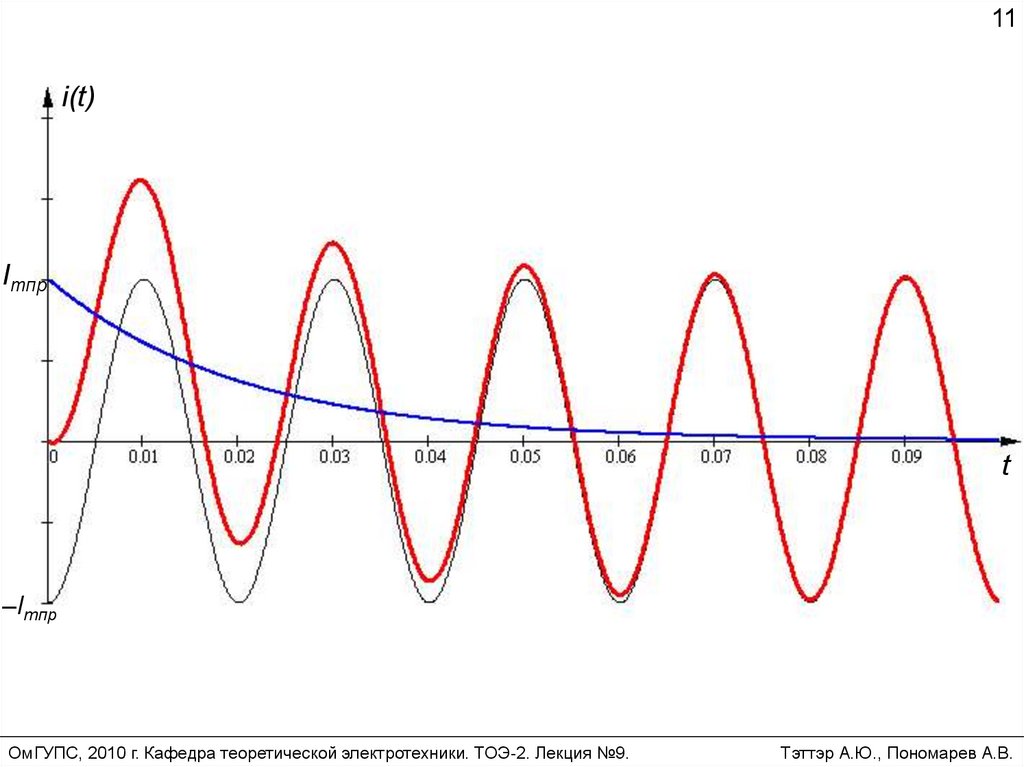
Если коммутация происходит при 2 , то10
начальное значение свободного тока iсв(t)
максимально, а именно i св 0 I m пр , и ток
переходного режима достигает экстремального
значения в конце первого полупериода.
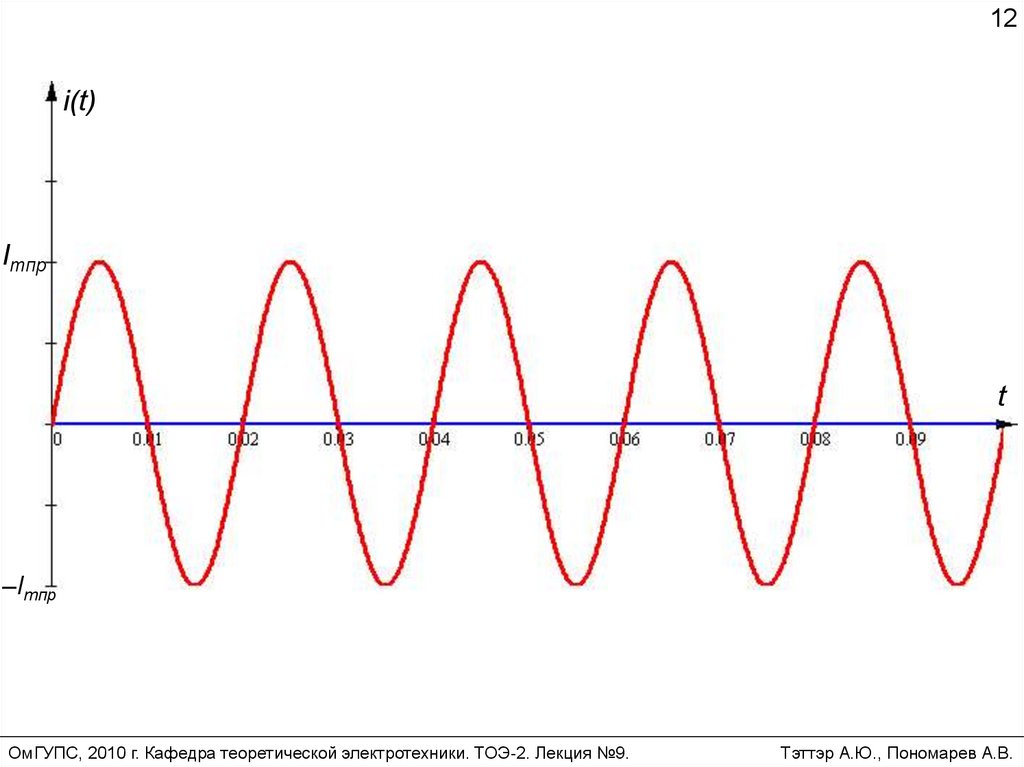
Если же коммутация происходит при = 0, то в
цепи сразу же наступает установившийся режим
без переходного процесса.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
11.
11i(t)
Imпр
t
–Imпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
12.
12i(t)
Imпр
t
–Imпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
13.
Включение цепи r,C на синусоидальноенапряжение
13
В момент времени t = 0 цепь, состоящая из
сопротивления r и емкости С, включается на
синусоидальное напряжение u U m sin t .
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
14.
14Исходное уравнение:
ur uC u,
где ur = r i ;
duC
i C
,
dt
или
duC
rC
uC U m sin t .
dt
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
15.
Характеристическое уравнение имеет вид:15
rCp 1 0
и, соответственно, корень уравнения
1
p .
rC
Переходное напряжение в цепи состоит из
суммы принужденной и свободной
составляющих:
uC uC пр uC св .
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №8.
Тэттэр А.Ю., Пономарев А.В.
16.
16Принужденную составляющую целесообразно
рассчитывать комплексным методом:
1
j
U Сm пр j
I m пр U Сm пр e ;
C
где U Cm пр – амплитуда принужденной
составляющей напряжения на емкости;
90 – начальная фаза принужденной
составляющей напряжения
на емкости;
Im пр – комплексная амплитуда тока;
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №8.
Тэттэр А.Ю., Пономарев А.В.
17.
17j
U m Ume
j
j
I m пр e
Im пр e ;
I m пр
j
Z
ze
1 – комплексное сопротивление;
Z r j
С
1
z r 2 2 – модуль комплексного сопротивления;
С
2
1
arctg С – аргумент комплексного сопротивления;
r
U m – амплитуда принужденной
Im пр
составляющей тока.
z
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №8.
Тэттэр А.Ю., Пономарев А.В.
18.
Мгновенное значение принужденной составляющейнапряжения на емкости
uC пр Jm U Cm пр e
j
e
j t
18
U Cm пр sin t .
Свободная составляющая
uC cв B е .
pt
Постоянная В определяется из уравнения:
uC (t ) U Cm пр sin t
1
t
Bе rC
при t = 0+
u C 0 u C пр 0 u C св 0 U Cm пр sin B.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №8.
Тэттэр А.Ю., Пономарев А.В.
19.
Величина uC(0+) находится на основании второгоправила коммутации:
19
uC 0 uC 0 0.
Следовательно,
0 U Cm пр sin B,
откуда
B U Cm пр sin .
Напряжение на емкости
uC U Cm пр sin t U Cm пр sin
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №8.
1
t
e rC .
Тэттэр А.Ю., Пономарев А.В.
20.
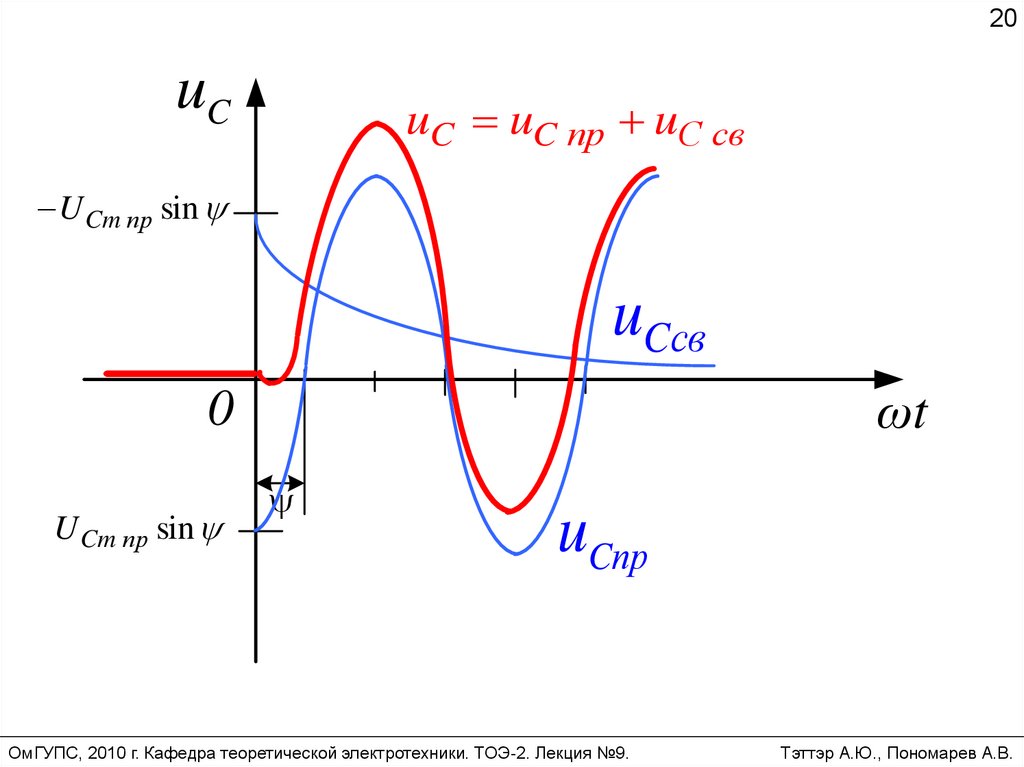
20uC
uC uC пр uC св
U Cm пр sin
uCсв
ωt
0
U Cm пр sin
uCпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
21.
Если коммутация происходит при 2 , то21
начальное значение свободной составляющей
напряжения на емкости uCcв(0) максимально, а
именно u Cсв 0 U Cm пр , и переходное
напряжение достигает экстремального значения в
конце первого полупериода.
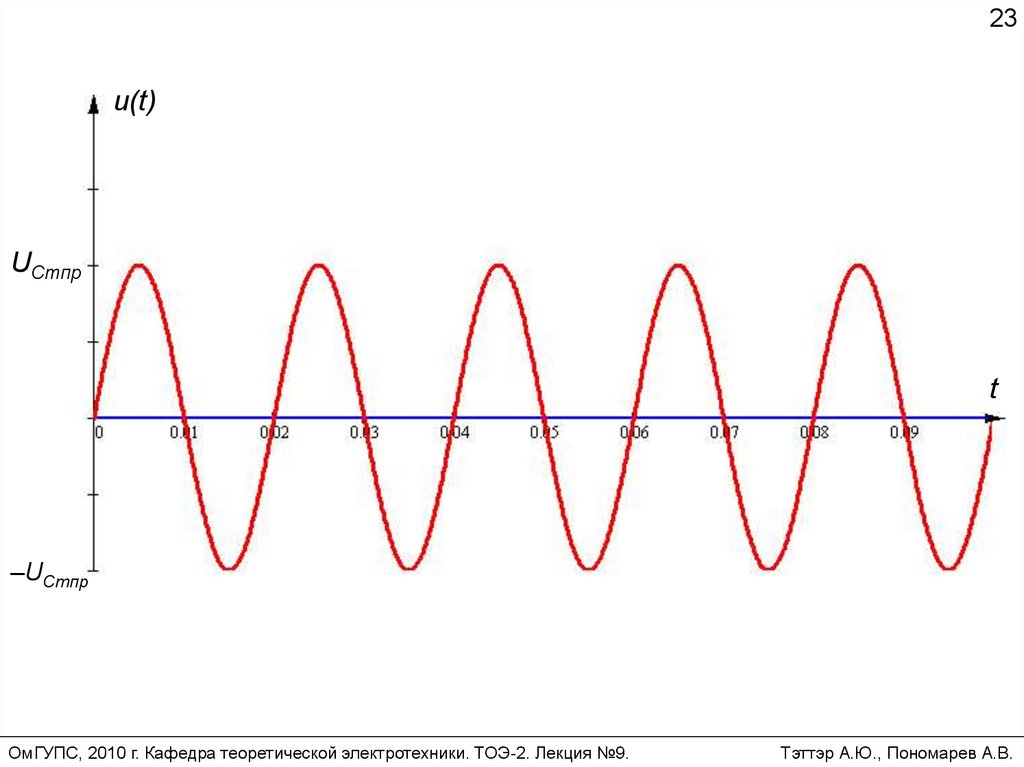
Если же коммутация происходит при = 0, то в
цепи сразу же наступает установившийся режим
без переходного процесса.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
22.
22u(t)
UCmпр
t
–UCmпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
23.
23u(t)
UCmпр
t
–UCmпр
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
24.
Этапы расчета переходных процессовКЛАССИЧЕСКИМ МЕТОДОМ
24
1. Расчет установившегося режима в схеме до
коммутации. Определение тока в индуктивности и
(или) напряжения на емкости.
2. Составление дифференциальных уравнений по
законам Кирхгофа для послекоммутационного
состояния цепи.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
25.
253. Определение принужденных составляющих
искомых токов и (или) напряжений из расчета
установившегося режима в схеме после
коммутации.
4. Формирование характеристического уравнения:
а) непосредственно из дифференциального;
б) через определитель алгебраизированной
системы дифференциальных уравнений;
в) по входному сопротивлению схемы.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.
26.
265. Определение начальных условий – значений
искомых токов и напряжений (при необходимости
и их производных) при t = 0+.
6. Нахождение постоянных.
ОмГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция №9.
Тэттэр А.Ю., Пономарев А.В.




















 physics
physics electronics
electronics








