Similar presentations:
Операторный метод расчета переходных процессов. Лекция 5
1. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
Сложность определения постоянныхинтегрирования при степени характеристического
уравнения выше второй сильно усложняет расчет
переходных процессов классическим методом.
Для инженерной практики более удобным является
метод решения линейных дифференциальных
уравнений, при котором заданные начальные
условия включаются в исходные уравнения и для
нахождения решения не требуется отдельно
определять постоянные интегрирования.
2.
Одним из таких методов является метод расчета переходныхпроцессов, основанный на преобразовании Лапласа, который
назван операторным.
Идея метода заключается в том, что из области функций
действительного переменного решение переносится в
область функций комплексного переменного p=a+jb, где
операции принимают более простой вид: вместо исходных
дифференциальных или интегродифференциальных
уравнений получатся алгебраические уравнения; затем
результат решения алгебраических уравнений
«интерпретируется», т.е. производится обратный переход в
область функций действительного переменного
аналитически или с помощью таблиц.
3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Будем под р понимать комплексное числоp = a + jb,
(2.28)
где а – действительная, а jb – мнимая части комплексного
числа.
Функцию времени (ток, напряжение, ЭДС, заряд) обозначают
f(t) и называют оригиналом. Ей соответствует функция F(p),
называемая изображением, определяемая в соответствии с
выражением:
F(p) f ( t )e ptdt .
(2.29)
0
Соответствие между функциями F(p) и f(t) записывают
следующим образом:
F(p) ≓ f(t).
(2.30)
4.
Знак «≓» называют знаком соответствия.Верхний предел интеграла (2.29) равен бесконечности.
Интегралы с бесконечным верхним пределом называют
несобственными. Если в результате интегрирования и
подстановки пределов получают конечное число (не
бесконечность), то говорят, что интеграл сходится.
В курсе математики доказывается, что интеграл (2.29), в
состав которого входит функция е–pt = e–ate–jbt, сходится
только в том случае, когда модуль функции f(t), если и
увеличивается с ростом t, то все же медленнее, чем модуль
функции еpt, равный еat.
Практически все функции f(t), с которыми имеют дело в
курсе ТОЭ, этому условию удовлетворяют.
5.
Определим изображения некоторых простейших функций.Изображение постоянной
Найдем изображение функции f(t) = A, где А —постоянная
величина. Для этого в (2.29) вместо f(t) подставим А и
выполним интегрирование:
F(p) Ae
0
pt
pt
1
Ae
pt
dt A d(e )
p
p 0
A
.
p
0
Следовательно, изображение постоянной равно самой
постоянной, деленной на р:
А ≓ А/р.
(2.31)
6.
Изображение показательной функции еatВместо f(t) подставим в (2.29) еat:
1
e at e ptd t (p a)
F(p) e at e ptdt e t ( p a ) dt
p a 0
0
0
1 t ( p a )
1
1
e
(0 1)
.
0
p a
p a
p a
Таким образом,
eat ≓ 1/(p – a).
(2.32)
При выводе формулы (2.32) (при подстановке пределов) было
учтено, что действительная часть оператора р больше, чем a, т.
е. а > a. Только при этом условии интеграл сходится.
Положив в формуле (8.28)
1
jw t
a jw, получим
(2.33)
e
.
p jw
7.
Формула (2.33) позволяет найти изображение комплексасинусоидального тока:
j( w t )
jw t
I m e
Ime
.
С этой целью обе части (2.33) умножим на постоянное число
Im:
1
I e jw t I
.
(2.34)
m
m
p jw
Аналогично, изображение комплекса синусоидального
напряжения
e jw t U
U
m
m
1
.
p jw
(2.35)
Функции е–at соответствует изображение:
e
a t
1
.
p a
(2.36)
8.
Изображение производныхПусть функции f(t) соответствует изображение F(p).
Требуется найти изображение первой производной df(t)/dt,
если известно, что значение функции f(t) при t = 0 равно f(0).
Подвергнем функцию df(t)/dt преобразованию Лапласа:
df ( t ) pt
pt
e
dt
e
dt
d f (t ) .
0
0
Положим е–pt = u, d[f(t)] = dv и применим формулу
интегрирования по частям:
e d f (t ) e
0
pt
pt
f ( t ) 0 f ( t )d e pt pF(p) f (0), (2.37)
0
9.
посколькуe pt f ( t ) 0 0 f (0) f (0),
а
Поэтому
f (t )d e pt p f ( t )e ptdt pF(p).
0
0
df(t)/dt ≓pF(p) – f(0).
(2.38)
Повторным применением операции, выражаемой формулой
(2.38), можно распространить теорему о дифференцировании
на производные высших порядков:
f"(t) = p[рF(p) – f(0)] – f‘(0) = p2F(p) – pf(0) – f'(0)
и т. д., откуда
n
f ( n ) ( t ) p n F(p) f ( k 1) (0)p n k
1
10.
Если, в частности, f(0) = f/(0) = ... = f(n-1)(0) = 0, тои, следовательно, n-кратному дифференцированию
оригинала соответствует n-кратное умножение на р (если все
производные при t=0 равны нулю).
Выражение (2.38) позволяет получить изображение
напряжения на индуктивном элементе. Как известно,
напряжение на индуктивности uL = L di/dt. Пусть оригиналу
тока i соответствует изображение I(p), т.е. i ≓ I(p). Тогда,
найдя в соответствии с (2.38) изображение дифференциала
тока, получим:
uL = L di/dt ≓ рLI(p) – Li(0),
(2.39)
где i(0) – значение тока в момент времени t = 0–.
Если i(0) = 0, то
uL ≓ LpI(p).
11.
Ниже приведены схема замещения индуктивности (а) и ееоператорная схема (б).
L
i
a
pL
I(p)
Li(0)
b
12.
Изображение интеграловt
Требуется найти изображение функции f ( t )dt, если
0
известно, что функции f(t) соответствует изображение F(p).
Подвергнем функцию преобразованию Лапласа:
t
pt
pt .
1 t
f ( t )dt e
0 0
dt
f ( t )dt d e
p
0 0
t
pt
pt
1 t
f ( t )dt e dt p f ( t )dt d e
0 0
0 0
Положим
и проинтегрируем по частям:
t
pt
f
(
t
)
e
dt
pt
pt 0
1 t
1 t
f ( t )dt d e f ( t )dt e
0
p 0 0
p 0
p
F(p)
.
p
13.
Первое слагаемое правой части при подстановке и верхнегои нижнего пределов обращается в нуль. При подстановке
верхнего предела нуль получается за счет обращения в нуль
экспоненты при t = , при подстановке нижнего предела
нуль получим за счет обращения в нуль интеграла функции
f(t).
t
F (p )
Таким образом,
0 f (t )dt p .
(2.40)
Повторное применение операции, выраженной этой
формулой, дает:
t
t
F (p )
(2.41)
... f ( t )dt
0
0
pn
Выражение (2.40) позволяет получить изображение
напряжения на емкостном элементе. Как известно,
напряжение на емкости определяется выражением
t
1
u C u C (0) idt .
C0
14.
Тогда, найдя в соответствии с (2.40) изображение интегралатока и учтя, что изображение начального напряжения uC(0)
на конденсаторе согласно (2.31) равно uC(0)/p, получим:
uC ≓ I(p)/Cp + uC(0)/p.
(2.42)
Ниже приведены схема замещения емкости (а) и ее
операторная схема (б).
C
i
a
1/pC
i
uC(0)/p
b
15. ЗАКОНЫ ОМА И КИРХГОФА В ОПЕРАТОРНОЙ ФОРМЕ. ВНУТРЕННИЕ ЭДС
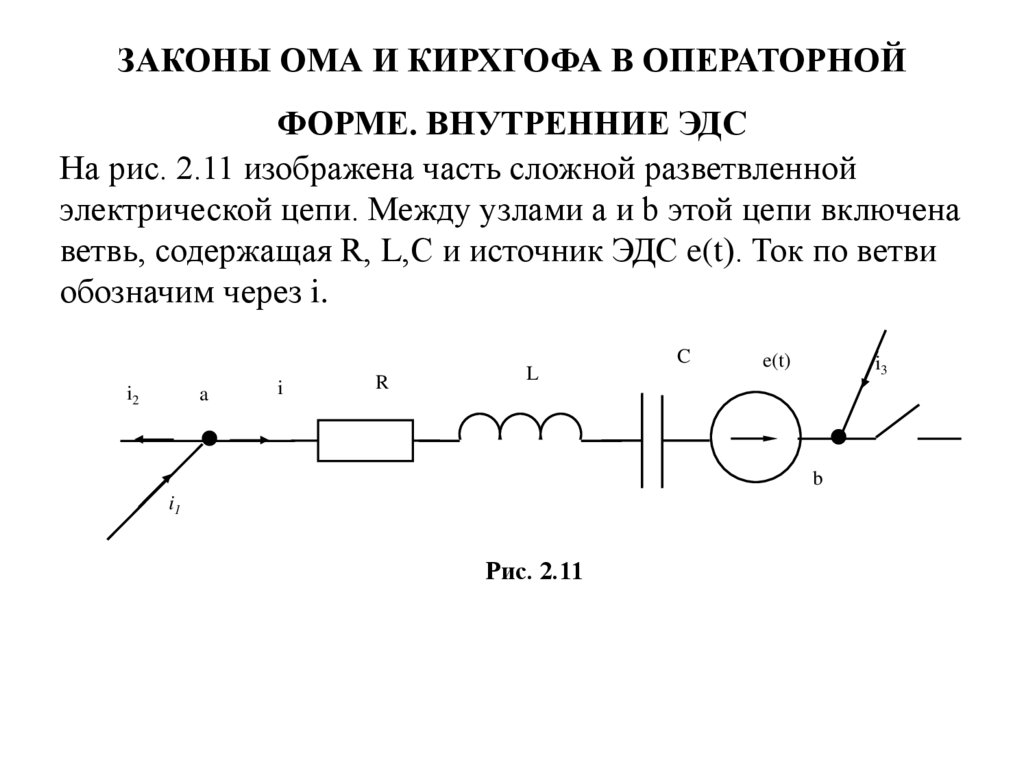
На рис. 2.11 изображена часть сложной разветвленнойэлектрической цепи. Между узлами а и b этой цепи включена
ветвь, содержащая R, L,С и источник ЭДС e(t). Ток по ветви
обозначим через i.
i2
a
i
R
L
C
e(t)
i3
b
i1
Рис. 2.11
16.
Замыкание ключа приводит к переходному процессу в схеме.Пусть до коммутации ток i = i(0–) и напряжение на
конденсаторе uC = uC(0–). Запишем выражение для
напряжения uab для послекоммутационного режима:
uab = a – b = uC + uL + uR – e(t),
или
di
1t
(2.50)
u ab iR L u C (0) idt e( t ).
dt
C0
К уравнению (2.50) применим преобразование Лапласа. В
силу линейности преобразования Лапласа изображение
суммы равно сумме изображений.
К уравнению (2.50) применим преобразование Лапласа. В
силу линейности преобразования Лапласа изображение
суммы равно сумме изображений.
17.
Каждое из слагаемых уравнения (2.50) заменим егооператорным изображением:
u C ( 0)
1
U ab (p ) I(p ) R pL
Li (0)
E(p ).
pC
p
1
pC
(2.51)
где
– операторное сопротивление
участка цепи между точками а и b. Структура его аналогична
структуре комплекса сопротивления того же участка цепи
переменному току, при замене jw на р.
Комплексное число р = a + jb может быть записано в виде р =
j(b – jа) = jW, где W =b – ja – комплексная частота; Z(p)=Z(jW)
– сопротивление, оказываемое рассматриваемой цепью
воздействию UejWt = U еpt, подобно тому как Z(jw) есть
сопротивление, оказываемое воздействию U еjwt. Поэтому
Z(p) называют сопротивлением для комплексной частоты.
Z(p ) R pL
18.
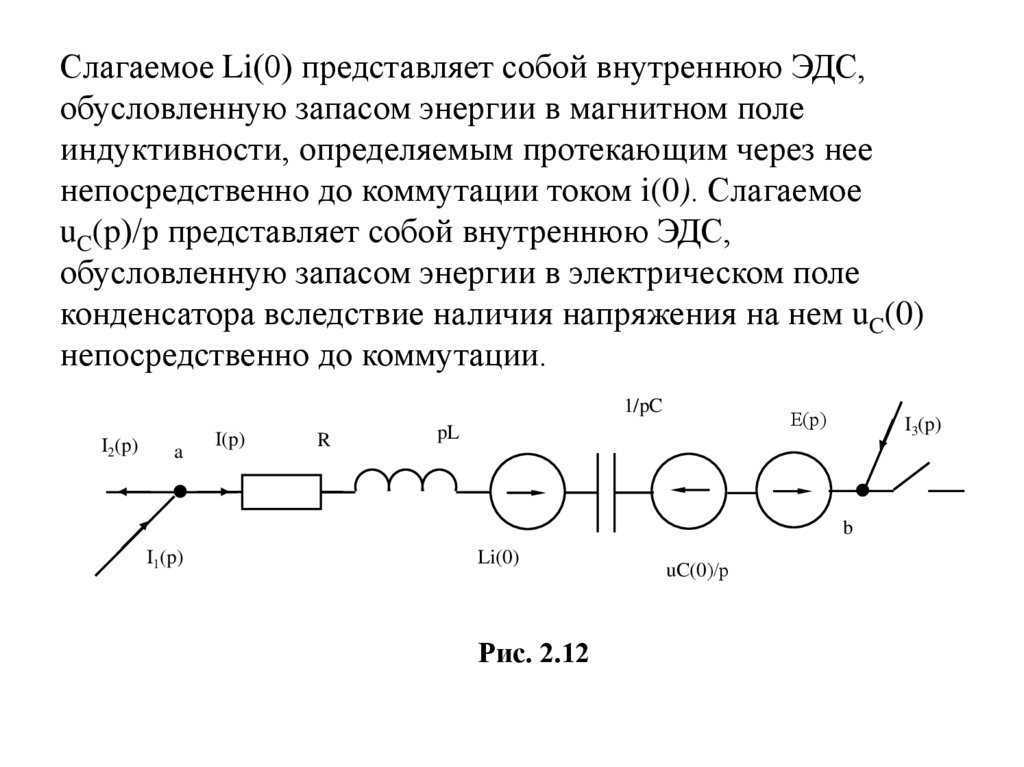
Слагаемое Li(0) представляет собой внутреннюю ЭДС,обусловленную запасом энергии в магнитном поле
индуктивности, определяемым протекающим через нее
непосредственно до коммутации током i(0). Слагаемое
uC(p)/р представляет собой внутреннюю ЭДС,
обусловленную запасом энергии в электрическом поле
конденсатора вследствие наличия напряжения на нем uC(0)
непосредственно до коммутации.
1/pC
I2(p)
a
I(p)
R
Е(р)
pL
I3(p)
b
I1(p)
Li(0)
Рис. 2.12
uC(0)/р
19. ПЕРВЫЙ ЗАКОН КИРХГОФА В ОПЕРАТОРНОЙ ФОРМЕ
По первому закону Кирхгофа, алгебраическая суммамгновенных значений токов, сходящихся в любом узле
схемы, равна нулю. Так, для узла а схемы рис. 2.13
i1 – i2 + i3 = 0
Применим преобразование Лапласа к уравнению (2.54) и
воспользуемся тем, что изображение суммы равно сумме
изображений:
I1(p) – I2(p) +I3(p) = 0.
a
i1
i2
i3
Рис. 2.13
20.
В общем случаеI(p) 0.
(2.55)
Уравнение (2.55) является записью первого закона Кирхгофа
в операторной форме.
21. ВТОРОЙ ЗАКОН КИРХГОФА В OПEРАТОРНОЙ ФОРМЕ
Для любого замкнутого контура любой электрической цепиможно составить уравнение по второму закону Кирхгофа для
мгновенных значений. Предварительно необходимо выбрать
положительные направления для токов в ветвях и
направление обхода контура.
е2(t)
C2
a
i2
R2
b
R3
L1
i1
R1
i3
R4
d
i4
Рис. 2.14
е4(t)
c
22.
Запишем для контура рис. 2.14 уравнение по второму законуKирхгофа при его обходе по часовой стрелке.
При составлении уравнения учтем, что начальное
напряжение на конденсаторе равно uC(0) и прием, что оно
действует согласно с током i2. Пусть начальное значение тока
i1 = i1(0). Тогда
t
di 1
1
i 1R1 L1 i 2 R 2 u C 2 (0)
i 2dt i 3 R 3 i 4 R 4 e2(t ) e4(t ).
dt
C2 0
Заменим каждое слагаемое его операторным изображением
(см. 2.13), объединим слагаемые с I1(p), I2(p), I3(p) и
перенесем в правую часть внутренние ЭДС uC(0)/p и L1i1(0).
В результате получим:
I1 (p)Z1(p) I 2 (p)Z2(p) I 3 (p)Z3(p) I 4 (p)Z4(p) E2(p) E4(p) EBH (p),
23.
гдеZ1(p ) R1 pL1,
1
Z2(p ) R 2
,
pC 2
Z3(p ) R 3, Z4(p ) R 4,
u ( 0)
EBH (p ) L1 i 1 (0) C 2 .
p
Это уравнение, записанное в более общем виде,
I (p)Z (p) E (p).
k
k
k
(2.56)
представляет собой математическую запись второго закона
Кирхгофа в операторной форме. В состав Ek(p) в общем
случае входят и внутренние ЭДС.
24. СОСТАВЛЕНИЕ УРАВНЕНИЙ ДЛЯ ИЗОБРАЖЕНИЙ
Уравнения для изображений по форме аналогичныуравнениям, составленным для той же цепи с помощью
символического метода для комплексов токов и напряжений.
Все, основанные на законах Кирхгофа приемы и методы
составления уравнений (методы эквивалентного генератора,
контурных токов, узловых потенциалов, наложения и т.д.)
можно применить и при составлении уравнений для
изображений.
При составлении уравнений для изображений ненулевые
начальные условия учитывают путем введения "внутренних"
ЭДС, обусловленных начальными токами через индуктивные
элементы и начальными напряжениями на конденсаторах.
25. ПЕРЕХОД ОТ ИЗОБРАЖЕНИЙ К ФУНКЦИИ ВРЕМЕНИ
Вторым этапом операторного метода расчета переходныхпроцессов является обратный переход от изображений к
функциям времени. Этот переход может быть выполнен
различными способами.
Наиболее простым способом перехода от изображений к
функции времени является способ, заключающийся в
непосредственном применении формул соответствия между
функциями оператора р и функциями времени t, которые
приводятся в справочной литературе.
Однако, этот способ требует достаточного большого опыта
решения дифференциальных уравнений.
26.
В общем случае изображение тока или напряжения всегдаM (p )
приводится к виду
.
N (p )
Студентам рекомендуется использовать так называемую
формулу разложения, которая приводится ниже без вывода.
M(p)
M(p i ) pi t
e
N(p) n N (p i )
где рi – i-й корень характеристического уравнения, которое
получается приравниванием нулю знаменателя N(p); N (p i )–
значение производной знаменателя относительно рi.
Левая часть формулы является функцией р, правая часть –
соответствующая ей функция времени t.
27.
Если изображение токато
M (p )
I (p )
N (p )
(2.57)
M( p i ) p i t
i( t )
e
n N (p i )
(2.58)
28. ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА ОПЕРАТОРНЫМ МЕТОДОМ
Расчет переходного процесса операторным методом состоитиз двух основных этапов:
• составления изображения искомой функции времени, в
который входит расчет независимых начальных условий,
составление операторной схемы цепи, вывод изображения
рассчитываемого искомой функции в виде уравнения
(2.57);
• перехода от изображения к функции времени.


























 physics
physics








