Метод расчета переходных процессов в линейной электрической цепи

1. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Обязательными этапами расчета переходных процессов
любым методом в линейной электрической цепи
являются:
• расчет мгновенных значений токов через индуктивности
и напряжений на емкостях непосредственно до
коммутации (расчет независимых начальных условий);
• составление характеристического уравнения и
определение его корней;
• определение выражений и расчет искомых токов и
напряжений как функции времени.
Расчет независимых начальных условий является
обязательным для всех методов расчета переходных
процессов. Способ составления характеристического
уравнения и алгоритм последнего этапа различается в
зависимости от метода.

2.

В классическом методе расчета отдельно рассчитывают
принужденные и свободные составляющие токов и
напряжений, а общее решение представляет собой сумму
принужденной и свободной составляющих. Определение
постоянных интегрирования, входящих в выражение для
свободного тока (напряжения), производят путем
совместного решения системы линейных алгебраических
уравнений по известным значениям корней
характеристического уравнения, а также по известным
значениям свободной составляющей тока (напряжения) и их
производных, взятых при t = 0+.

3. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ИНТЕГРИРОВАНИЯ В КЛАССИЧЕСКОМ МЕТОДЕ

Для любой схемы с помощью уравнений Кирхгофа и
законов коммутации можно найти:
числовое значение искомого свободного тока при t =
0+, обозначим его iсв(0+);
числовое значение первой, а если понадобится, то и
высших производных от свободного тока, взятых
при t = 0+. Числовое значение первой производной
от свободного тока при t = 0+ обозначим i св (0+);
второй – i св(0+); и т. д.
Рассмотрим способ определения постоянных
интегрирования A1,A2,..., полагая известными
iсв(0+), i св(0+), i св(0+) и значения корней p1, p2, ....

4.

Если характеристическое уравнение цепи представляет собой
уравнение первой степени, то iсв = Aept. Постоянную
интегрирования А определяют по значению свободного тока
iсв(0+):
A = iсв(0+).
(18)
Если дано характеристическое уравнение второй степени и
его корни действительны и не равны, то
(19)
p1t
p 2t
i св A1e
A 2e .
Продифференцируем это уравнение по времени:
i св p1 A1ep1t p 2 A 2ep2t .
(20)

5.

Запишем уравнения (19) и (20) для момента коммутации t =
0+ с учетом, того, что при t = 0+
ep1t ep2t 1.
В результате получим
i св (0 ) A 1 A 2 ;
i св (0 ) p 1 A 1 p 2 A 2 .
(21)
(22)
В этой системе уравнений известными являются его iсв(0+),
i св(0+), p1 и p2, неизвестными – А1 и А2
Совместное решение (21) и (22) дает
i св (0 ) p 2 i св (0 )
A1
,
p1 p 2
A 2 i св (0 ) A 1 .
(23)

6.

Для цепи, имеющей характеристическое уравнение третьей
степени, свободный ток
(24)
i св A1ep1t A 2ep2t A 3ep3t .
Найдем первую и вторую производные от обеих частей
уравнения (20):
(25)
i p A ep1t p A ep2t p A ep3t ;
св
1
1
2
2
3
3
i св p12 A1ep1t p 22 A 2ep2t p 23 A 3ep3t .
(26)
Запишем (24) – (26) при t = 0+:
i св (0 ) A 1 A 2 A 3 ;
i св (0 ) p 1 A 1 p 2 A 2 p 3 A 3 ;
2
2
2
i св (0 ) p 1 A 1 p 2 A 2 p 3 A 3 .
(27)

7.

Система уравнений (27) представляет собой систему трех
линейных алгебраических уравнений с тремя неизвестными:
А1, А2 и А3. Все остальные входящие в нее величины [p1, p2,
p3, iсв(0+), i св(0+), i св(0+)] известны.
При двух корнях характеристического уравнения для
определения постоянных интегрирования достаточно, чтобы
были известны величины свободных токов и напряжений и
их производных. Величины свободных составляющих
определяются как разность начальных условий и
принужденных составляющих при t = 0+. Согласно (8)
i(0+) = iПР(0+) + iCB(0+),
откуда
iCB(0+) = i(0+) – iПР(0+) = А1 + А2

8.

Производные токов и напряжений найдем из выражений
напряжения на индуктивности и тока через емкость.
u L CB (0 ) L
откуда
di L CB (0 )
dt
di L CB (0 )
dt
;
u L CB (0 )
L
;
i C CB (0 ) C
du C CB (0 )
dt
du C CB (0 )
dt
,
i C CB (0 )
C
Определение третьих производных токов и напряжений и
выше достаточно сложно, поэтому классический метод
расчета переходных процессов в электрических цепях
применения не нашел.

9. ПЕРЕХОДНЫЙ ПРОЦЕСС В RL–ЦЕПИ ПРИ ВКЛЮЧЕНИИ ЭДС

Рассмотрим электрическую цепь, изображенную на рис. 12.
Так как ток через индуктивность не может измениться
скачком, то в момент времени t(0+) тока в цепи нет. Поэтому
в схеме для определения начальных условий индуктивность
можно заменить разрывом. Начальными условиями
являются: i(0+) = 0; uL(0+) = e(0–).
r
r
а
i(t)
е(t)
а
L
i(0+) = 0
e(t)
b
а
b
б
Рис. 12. Включение RL-цепи. а – исходная схема; б – схема для
расчета начальных условий

10.

Характеристическое уравнение имеет вид
r + pL = 0,
r
и соответственно корень характеристического уравнения p
L
Переходный ток в цепи равен сумме принужденной и
свободной составляющей, которые определяются через e(t), r и
L.
i(t ) i ПР (t ) i СВ (t )
r
t
L
где i СВ ( t ) Ae
.
Рассмотрим случаи, когда ЭДС постоянная и равна Е и когда
она синусоидальная e(t) = Emsin(wt + Y).
При включении цепи к постоянной ЭДС принужденная
Е
i
составляющая тока равна ПР
,
r
поскольку сопротивление индуктивности постоянному току
равно нулю.

11.

Постоянная интегрирования А находится из начальных
условий при t = 0(+).
i(0 ) i ПР (0 ) i СВ (0 ) i ПР (0 ) A
E
A
откуда
.
r
Таким образом, переходный ток в цепи равен
E
i(t ) (1 e
r
r
t
L
)
Переходное напряжение на индуктивности выразится как
u L (t ) u ПР (t ) u СВ (t )

12.

При постоянной ЭДС в цепи принужденная составляющая
напряжения равна нулю, поэтому
u L (0 ) u ПР (0 ) u СВ (0 ) u СВ (0 ) A
откуда А = Е.
Таким образом, переходное напряжение на индуктивности
выражается как
u(t ) E e
r
t
L
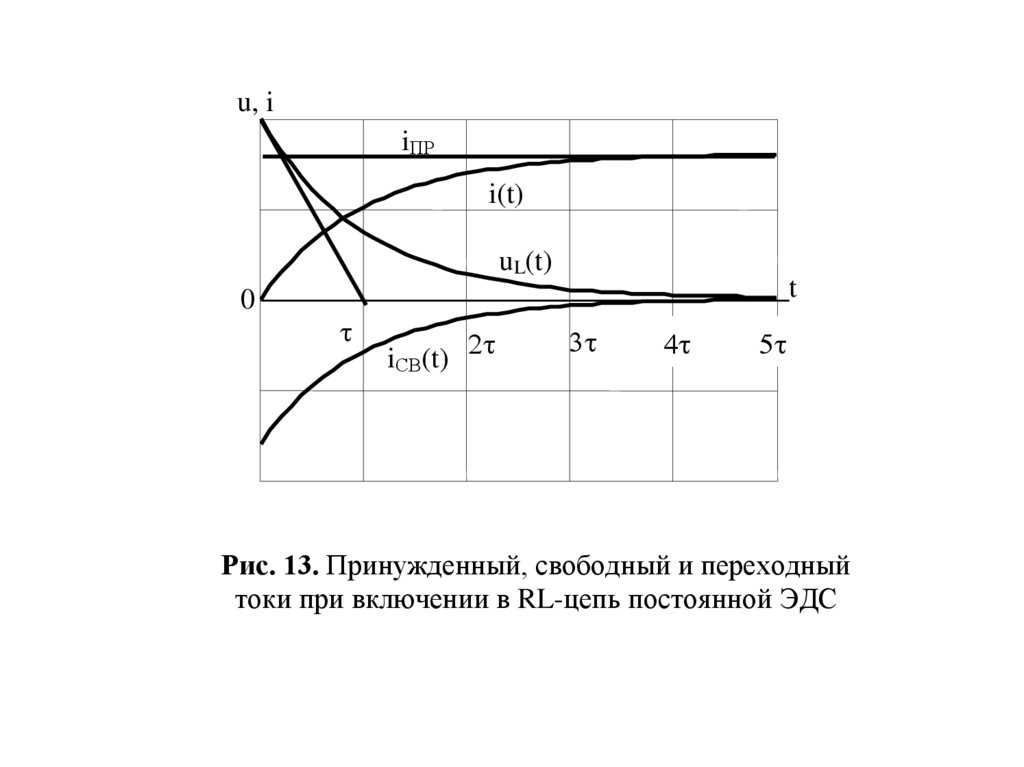
Графики принужденной составляющей тока, свободных и
полных составляющих тока и напряжения приведены на рис.
13.

13.

u, i
iПР
i(t)
uL(t)
0
iСВ(t)
t
Рис. 13. Принужденный, свободный и переходный
токи при включении в RL-цепь постоянной ЭДС

14.

При включении синусоидальной ЭДС e = Emsin(wt + Y)
характеристическое уравнение остается тем же, так как
определяется только параметрами цепи и не зависит от
величин и фаз источников электрической энергии. Не
изменяется также схема цепи для определения начальных
условий (рис. 12, б).
Определим начальные условия.
i(0+) = i(0–) =0; uL(0+) = Em sin( w 0 Y) Em sin Y .
Принужденные составляющие определятся символическим
методом через комплексные величины
I ПР max
где
wL
arctg (
)
r
E
m
r jwL
Em
r 2 ( wL ) 2
e j( Y )

15.

Комплексному значению принужденного тока соответствует
мгновенное:
E
i( t )
sin( wt Y )
m
r (wL)
2
2
Постоянная интегрирования определяется из уравнения
Em
i(0 ) i ПР (0 ) A
r (wL)
2
2
sin( Y ) A
При нулевом значении i(0+)
A
Em
r (wL)
2
2
sin( Y )
Переходной ток
i(t ) i ПР (t ) i СВ (t )
Em
r ( wL )
2
2
(sin( wt Y ) sin( Y ) e
r
t
L
)

16.

Свободная составляющая напряжения на индуктивности
будет изменяться по экспоненциальному закону как
u L (t ) E m sin Y e
r
t
L
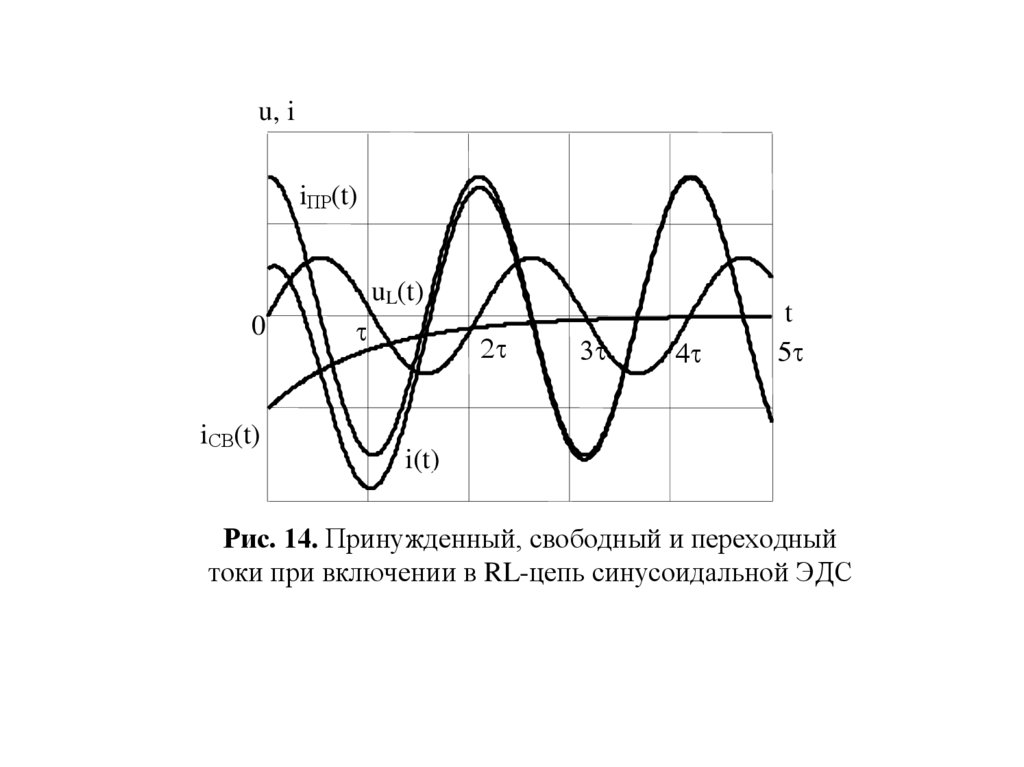
Графики принужденной составляющей тока, свободных и
полных составляющих тока и напряжения приведены на рис.
14.

17.

u, i
iПР(t)
0
iСВ(t)
uL(t)
t
i(t)
Рис. 14. Принужденный, свободный и переходный
токи при включении в RL-цепь синусоидальной ЭДС

18.

Анализ уравнения для свободного тока показывает, что его
начальное значение зависит от соотношения активного и
реактивного сопротивлений и от начальной фазы ЭДС.
Начальное значение свободного тока тем меньше, чем
меньше разность Y - . Если эта разность равна нулю или p,
будет равна нулю и свободная составляющая тока, т.е.,
переходного тока при подключении синусоидальной ЭДС не
будет. А так как напряжение на индуктивности равно
произведению индуктивности на производную тока, не будет
и переходного напряжения, т.е., переходного процесса в цепи
не будет.
В цепях синусоидального тока при коммутациях могут
быть случаи, когда переходного процесса не будет.

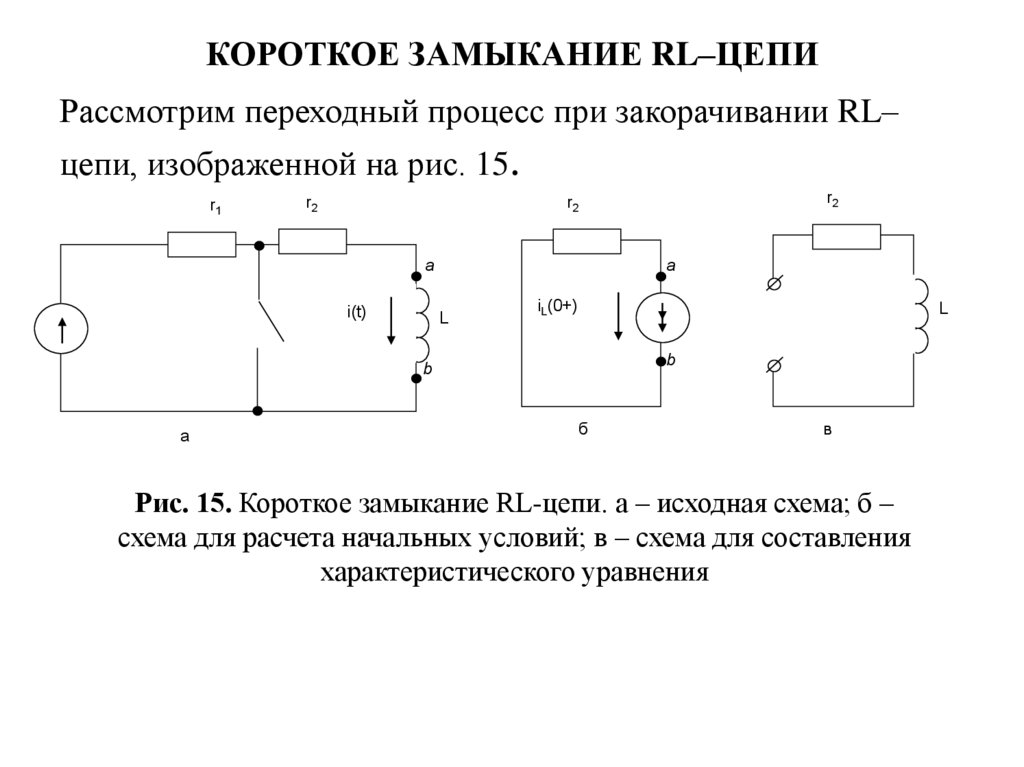
19. КОРОТКОЕ ЗАМЫКАНИЕ RL–ЦЕПИ

Рассмотрим переходный процесс при закорачивании RL–
цепи, изображенной на рис. 15.
r1
r2
а
i(t)
а
L
iL(0+)
L
b
b
а
r2
r2
б
в
Рис. 15. Короткое замыкание RL-цепи. а – исходная схема; б –
схема для расчета начальных условий; в – схема для составления
характеристического уравнения

20.

В отличие от предыдущей задачи в этой независимые
начальные условия ненулевые. Через индуктивность
протекает ток, определяемый суммой активных
сопротивлений, если в цепи включена ЭДС постоянного тока,
и комплексным сопротивлением, если ЭДС синусоидальная.
Рассмотрим оба случая.
При постоянной ЭДС ток через индуктивность до
коммутации
Е
i ( 0 )
r1 r2 ,
при синусоидальной комплексное значение
докоммутационного тока
I max
где
E
E max
max
e j( Y )
r1 r2 jwL
(r1 r2 ) 2 (wL ) 2
arctg (
wL
)
r1 r2

21.

Мгновенное значение тока при t = 0+ получается как
i ( 0 )
Em
(r1 r2 ) (wL)
2
2
sin( Y )
Коммутацией ключа цепь делится на две, между собой не
связанные: левая состоит из ЭДС и сопротивления r1; правая
из сопротивления r2 и индуктивности L. Переходный
процесс имеет место только в правой части, где имеется
индуктивность. Так как в этой части цепи отсутствуют
источники электрической энергии, то принужденные
составляющие токов и напряжений равны нулю.
Следовательно, переходные ток и напряжение равны
соответственно свободному току и свободному напряжению.

22.

Характеристическое уравнение получаем через операторное
сопротивление, разомкнутой послекоммутационной схемы
(рис.15, в):
Z(p) = r2 + pL,
r2
p
откуда
.
L
Переходный ток при постоянной ЭДС
Е
i( t )
ept ,
r1 r2
при синусоидальной
i( t )
Em
(r1 r2 )2 (wL)2
sin( Y ) ept

23.

Напряжение на индуктивности равно напряжению на
сопротивлении r Оно выражается соответственно при
постоянной и синусоидальной ЭДС как
Е r2
u L (t )
e pt
r1 r2
u L (t )
Em r2
(r1 r2 )2 (wL)2
sin( Y ) ept

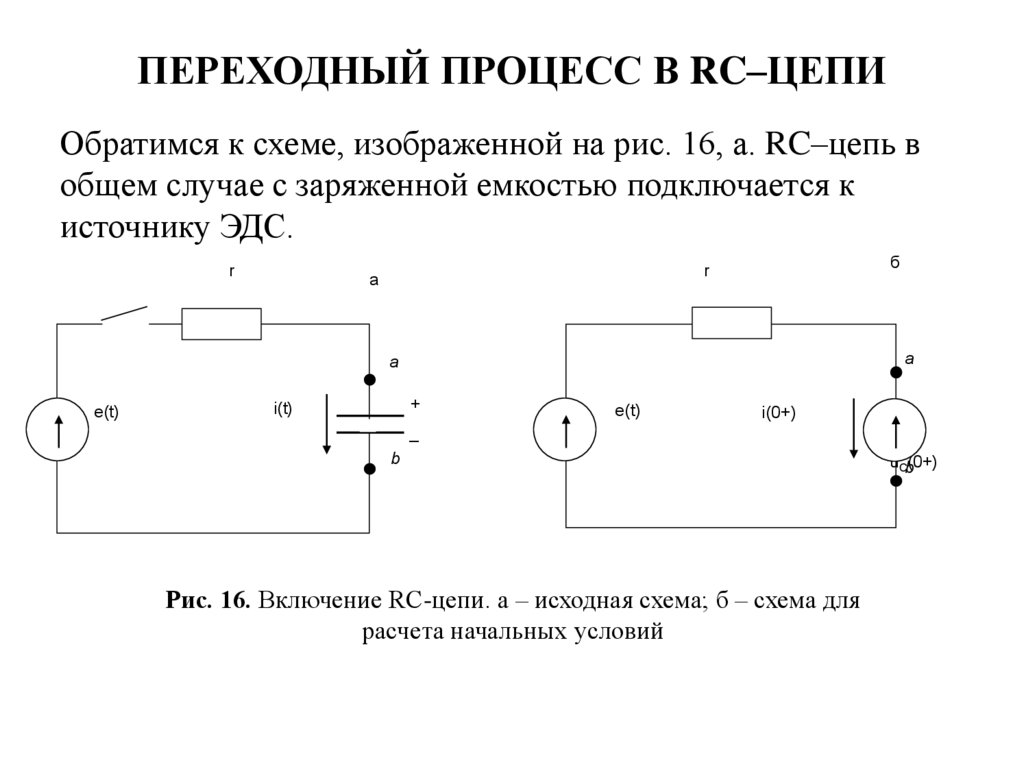
24. ПЕРЕХОДНЫЙ ПРОЦЕСС В RC–ЦЕПИ

Обратимся к схеме, изображенной на рис. 16, а. RC–цепь в
общем случае с заряженной емкостью подключается к
источнику ЭДС.
r
б
r
а
а
а
е(t)
+
i(t)
e(t)
i(0+)
–
b
Рис. 16. Включение RC-цепи. а – исходная схема; б – схема для
расчета начальных условий
uCb(0+)

25.

Согласно второму закону коммутации напряжение на емкости до
q
u C (0 ) , остается
коммутации, равное при заданном заряде
C
тем же после коммутации. Если емкость не заряжена
(подавляющее большинство цепей) напряжение на ней равно
нулю. Этот параметр является независимым начальным
условием. Зависимым начальным условием является ток в цепи:
e(0 ) u C (0 )
i(0 )
r
1
0
Характеристическое уравнение имеет вид: r
pC
откуда p
1
. Постоянная времени t = rC.
rC

26.

Принужденное напряжение на незаряженной емкости при
постоянной ЭДС
u C ПР E i ПР r E 0 r E
Если включена синусоидальная ЭДС, принужденные
составляющие тока и напряжения на емкости вычислим
сначала в комплексной форме записи, из которых получим
мгновенные значения:
i C ПР (t )
Em
1 2
r (
)
wC
sin( wt Y )
2
1
u C ПР (t )
wC
Em
1 2
r (
)
wC
2
sin( wt Y )
2

27.

Постоянная интегрирования А равна разности начального
условия и принужденной составляющей в момент времени
t(0+). При постоянной ЭДС в цепи с незаряженной емкостью
постоянная интегрирования напряжения на емкости
А = – Е,
при синусоидальной ЭДС
Em
1
A
sin( Y )
wC
2
1 2
2
r (
)
wC
Соответственно постоянные интегрирования токов:
E
A
r
A
Em
1 2
r (
)
wC
2
sin( Y )

28.

Переходные напряжение и ток при включении постоянной
ЭДС:
1
rC
1
Em
u(t ) E m e
i( t )
(1 e rC )
r
Если включается синусоидальная ЭДС, получаем:
1
u( t )
wC
i( t )
Em
1 2
r (
)
wC
2
Em
1 2
r (
)
wC
2
rC
(sin( Y ) sin( Y ) e )
2
2
(sin( wt Y ) sin( Y ) e
1
1
rC
)

29. ПЕРЕХОДНЫЙ ПРОЦЕСС В RLC–ЦЕПИ

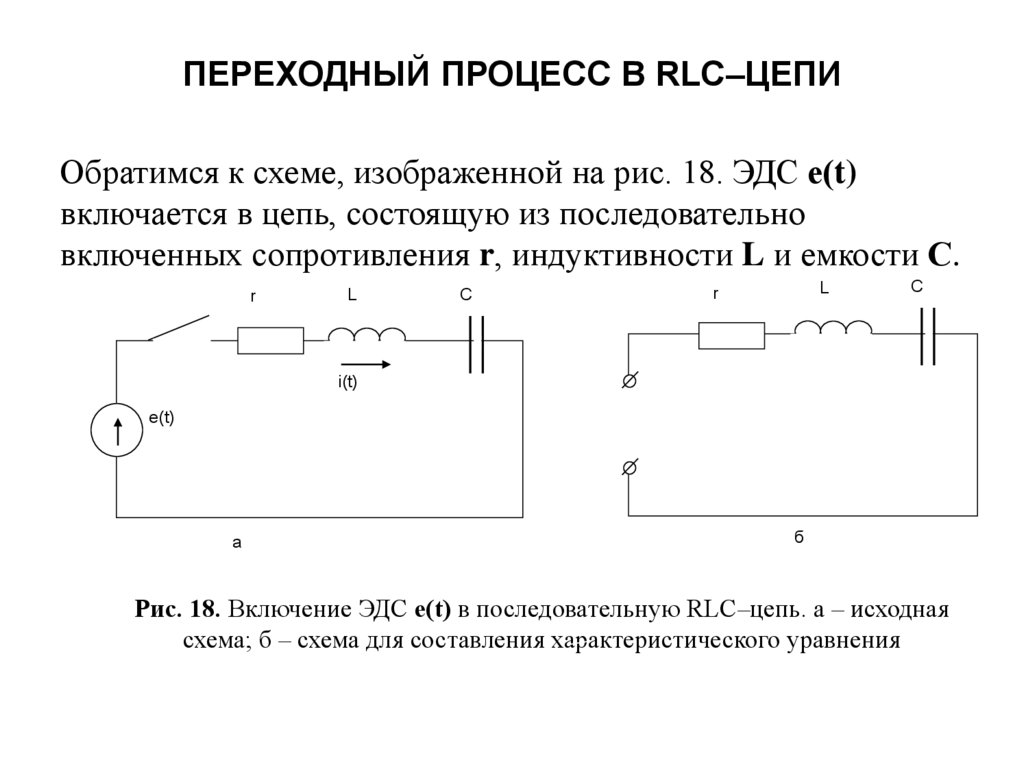
Обратимся к схеме, изображенной на рис. 18. ЭДС е(t)
включается в цепь, состоящую из последовательно
включенных сопротивления r, индуктивности L и емкости С.
r
L
C
L
r
C
i(t)
e(t)
а
б
Рис. 18. Включение ЭДС е(t) в последовательную RLC–цепь. а – исходная
схема; б – схема для составления характеристического уравнения

30.

1
L p r p 0
C
Характеристическое уравнение
2
имеет корни:
2
p 1, 2
r
1
r
2 w 02
2L
LC
2L
r
где
;
2L
w0
1
LC
– резонансная частота.
Поскольку имеем два корня характеристического уравнения,
свободный ток
i CB (t ) A1 ep1t A 2 ep2t
а ток в цепи
i(t ) i ПР (t ) A 1 e
p1t
A2 e
p 2t

31.

Принужденный ток определяется через заданную ЭДС и
параметры пассивных элементов.
В зависимости от соотношения и w0 свободные токи и
напряжения буду затухать либо апериодически, либо
колебательно. Если > w0, корни характеристического
уравнения будут отрицательными действительными, если <
w0 – комплексно сопряженными с отрицательной
действительной частью, В первом случае процесс затухания
свободных токов и напряжений апериодический, во втором –
колебательный. Примеры затухания свободных
составляющих приведены на рис. 19.

32.

а
i
0
t
0
в
i
б
i
г
i
t
0
0
t
t
Рис. 19. Затухание свободного тока в RLC–цепь. а – w ; б – = w
с – < w г – << w

33.

Если RLC – цепь подключается к источнику синусоидальной
ЭДС, то принужденный ток
iПР(t) = Imsin(wt + Y – ),
а полный
i(t ) I m sin( wt Y A 1 e p1t A 2 e p2t
Характер переходного процесса зависит только от
параметров пассивных элементов, но не от вида и величины
ЭДС. Переходные токи и напряжения могут стремиться к
принужденным либо апериодически, либо колебательно. При
этом свободная частота может быть больше принужденной,
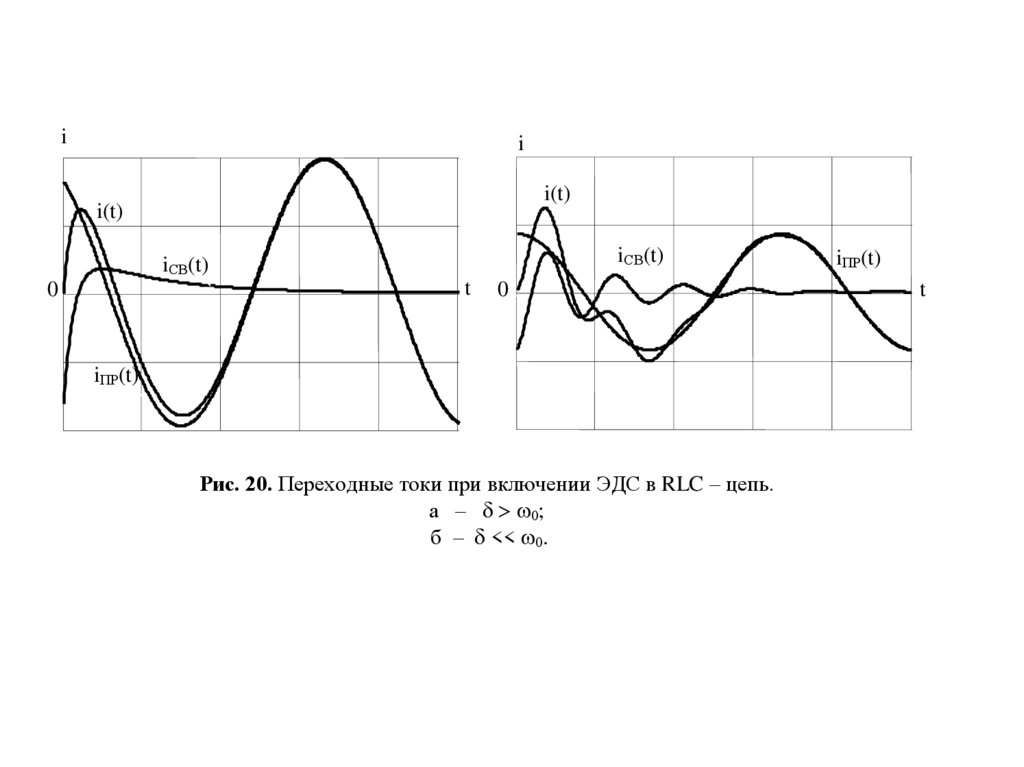
или меньше. На рис 20 показаны случаи апериодического и
колебательного переходного процесса.

34.

i
i
i(t)
i(t)
iСВ(t)
iСВ(t)
t
0
0
iПР(t)
Рис. 20. Переходные токи при включении ЭДС в RLC – цепь.
а – w ;
б – << w .
iПР(t)
t

35. РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА В РАЗВВЕТВЛЕННОЙ ЦЕПИ

В классическом методе расчета переходных процессов
отдельно рассчитываются принужденные составляющие
токов и напряжений, отдельно – свободные.
Принужденные составляющие определяются через величины
источников тока и ЭДС и параметры пассивных элементов
цепи. Если источники электрической энергии
синусоидальны, расчет производится символическим
методом с последующим переводом комплексных величин в
мгновенные синусоидальные.
Постоянные интегрирования свободных составляющих токов
и напряжений определяются через разности начальных
значений в момент времени t = 0+ и принужденных
составляющих в этот же момент времени.

36.

Таким образом, для вычисления переходных токов и
напряжений необходимо определить:
• начальные значения токов и напряжений, для чего
необходимо рассчитать докоммутационный режим и
получить независимые начальные условия;
• принужденные составляющие токов и напряжений;
• найти корни характеристического уравнения;
• рассчитать постоянные интегрирования. Для определения
постоянных интегрирования при двух корнях
характеристического уравнения требуется найти
производные свободных составляющих токов и
напряжений.