Similar presentations:
Расчет переходных процессов в электрических цепях классическим методом
1.
12.
Условие задачиРассчитать все переходные токи
цепи и переходное напряжение
на катушке индуктивности,
построить временные зависимости
входного тока электрической
цепи и напряжения на катушке
индуктивности.
2
3.
Исходные данные:E, В
R1,Ом R2,Ом R3,Ом L, мГ
10
10
i1
10
100
i3
i2
Е
L
R2
R1
120
R3
3
4.
РЕШЕНИЕi1
i3
i2
R2
Е
R1
R3
Составим систему
дифференциальных
L
уравнений по законам
Кирхгофа для режима
после коммутации:
4
5.
Принимаем за базовоеуравнение (3) и при помощи
уравнений (1) и (2) выразим ток
i1 через ток i3
5
6.
67.
Уравнение (5) подставим в уравнение (3)7
8.
В полученное уравнение подставимчисловые значения:
8
9.
Искомый токопределяется суммой двух
решений:
принуждённой и
свободной
составляющими:
9
10.
Расчёт принуждённой составляющейИскомый ток в установившемся
после коммутационном режиме
является постоянным, так как
источник ЭДС –
постоянный во времени.
Следовательно, производная тока в
уравнении (6) для установившегося
режима обращается в ноль.
10
11.
Тогда:Второй способ определения
установившегося тока
Рассмотрим заданную электрическую цепь
после коммутации в установившемся
режиме.
11
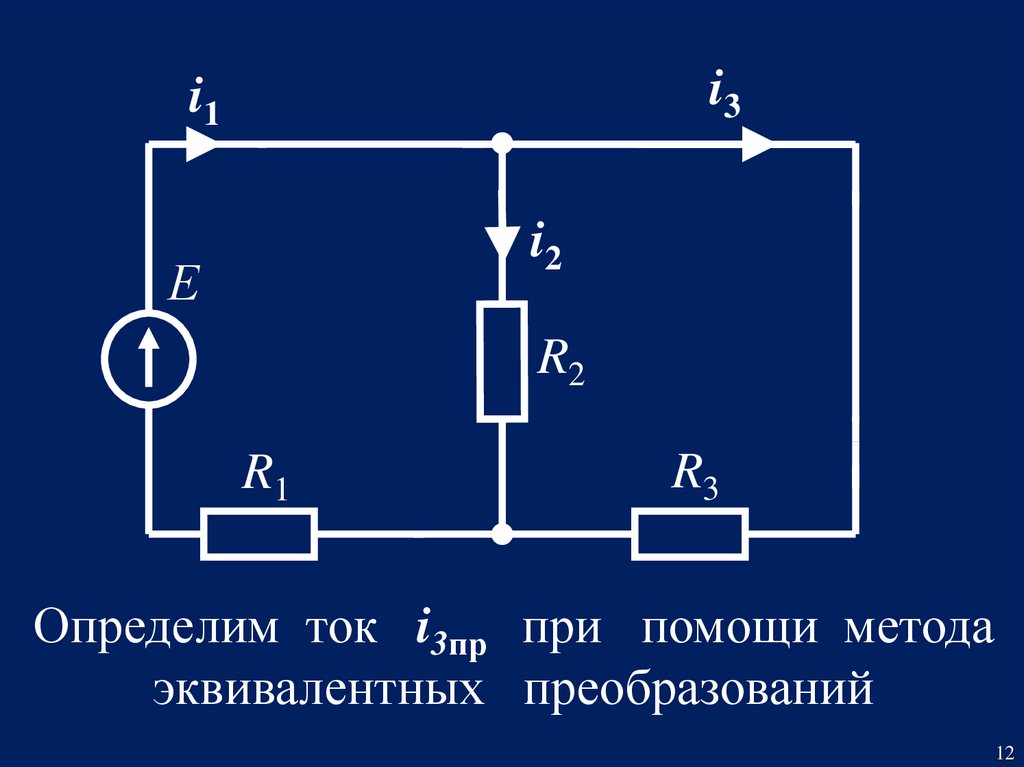
12.
i3пр.i1пр
i2пр.
Е
L
R2
R1
R3
Определим ток i3пр при помощи метода
эквивалентных преобразований
12
13.
i1прi3пр
i2пр
Е
R23
R1
R2
R3
13
14.
i1прЕ
R23
ЭКВ
R1
14
15.
i1прЕ
R23
U23
R1
15
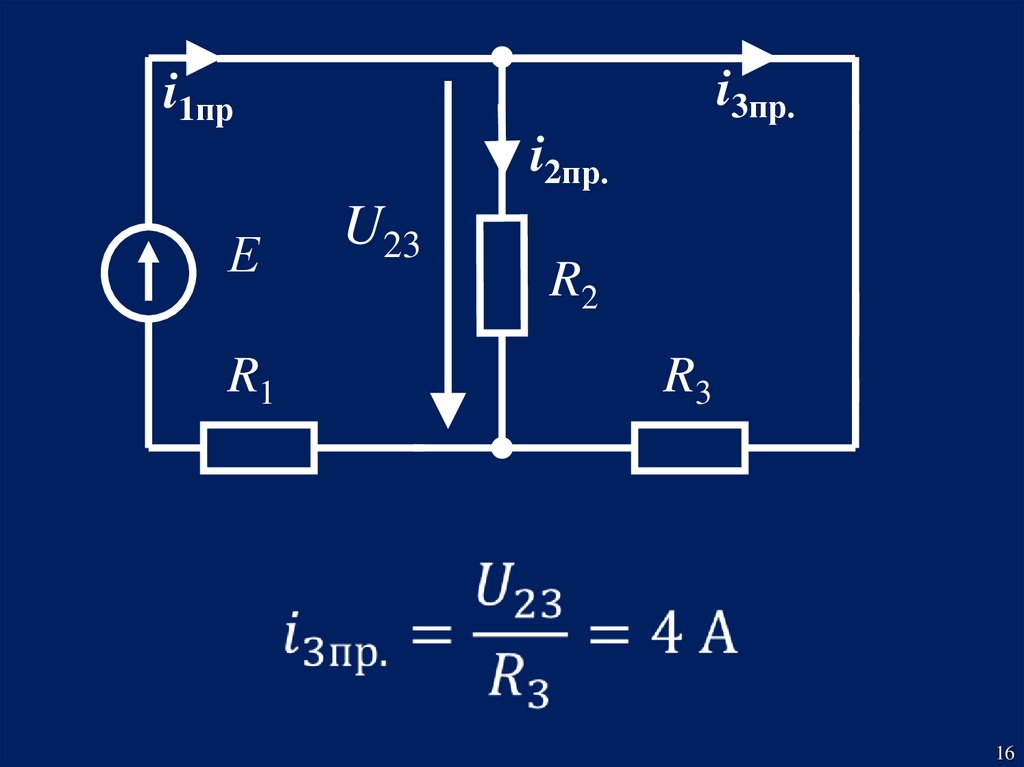
16.
i3пр.i1пр
i2пр.
Е
R1
U23
R2
R3
16
17.
Расчёт cвободной составляющейУравнение (6) приводим к однородному
и алгебраизируем его:
p
0
Определяем корень
алгебраического уравнения:
17
18.
Вид решения для свободнойсоставляющей тока:
Полное решение для
искомого тока:
18
19.
Определяем постояннуюинтегрирования А при помощи
начальных условий и закона
коммутации.
В соответствии с
I законом коммутации:
19
20.
В данном случае,так как до коммутации
источник отключён от цепи.
Следовательно, в момент коммутации
Тогда для момента времени t = 0
уравнение (7) приобретает
следующий вид:
20
21.
×00(0)
А=–4
Полное решение искомого тока
i3 (t) = 4 – 4е
–150t
21
22.
Определим остальные токи схемы припомощи исходной системы уравнений.
Из уравнения (5) определим ток i1:
i3 (t) = 4 – 4е –150t
i1 = 6 + 2 –
-150t
2е
i1 (t) = 8 – 2е
–150t
22
23.
Из уравнения (4) определим ток i2 :i1 = 8 – 2е –150t
i2 = 12 – 8 + 2е
i2 (t) = 4 + 2е
–150t
–150t
23
24.
Проверка:–150t
i2 (t) = 4 + 2е
+
i3 (t) = 4 – 4е
–150t
=
i1 (t) = 8 – 2е
–150t
24
25.
Определим закон изменения напряжения–150t
на 3катушке индуктивности
i (t) = 4 – 4е
uL (t) = 60е
–150t
25
26.
Определим время переходногопроцесса:
Шаг изменения времени для
построения графических
зависимостей:
26
27.
i1 (t)0
0,0033333
0,0066666
0,0099999
0,0133332
0,0166665
0,0199998
0,0233331
0,0266664
0,0299997
0,033333
0,0366663
0,0399996
0,0433329
6
6,787
7,264
7,554
7,729
7,836
7,900
7,94
7,963
7,978
7,987
7,992
7,995
7,997
Зависимость входного тока от времени
8,0
значения входного тока в А
t
7,0
6,0
5,0
4,0
3,0
2,0
1,0
0,0
0,000
0,010
0,020
0,030
0,040
значения времени в сек.
i1 (t)= 8 –2е-150t
27
28.
uL (t) = 60е –150tuL
0
0,0033333
0,0066666
0,0099999
0,0133332
0,0166665
0,0199998
0,0233331
0,0266664
0,0299997
0,033333
0,0366663
0,0399996
0,0433329
60
36,39
22,07
13,39
8,120
4,925
2,987
1,812
1,099
0,6666
0,4043
0,2452
0,1487
0,0902
Зависимость напряжения на катушке индуктивности от
времени
70
значения напряжения в В
t
60
50
40
30
20
10
0
0
0,01
0,02
0,03
0,04
значения времени в сек.
28
29.
2930. Методические указания с требованиями по оформлению и вариантами расчётно-графической работы приведены на сайте http://
vinokurovuniver.jimdo.com
30
31.
Номер вариантаопределяется
трёмя последними
цифрами
зачётной книжки
студента
31
32.
первая цифра—
соответствует номеру строки
из таблицы 1
вторая цифра —
соответствует номеру строки
из таблицы 2
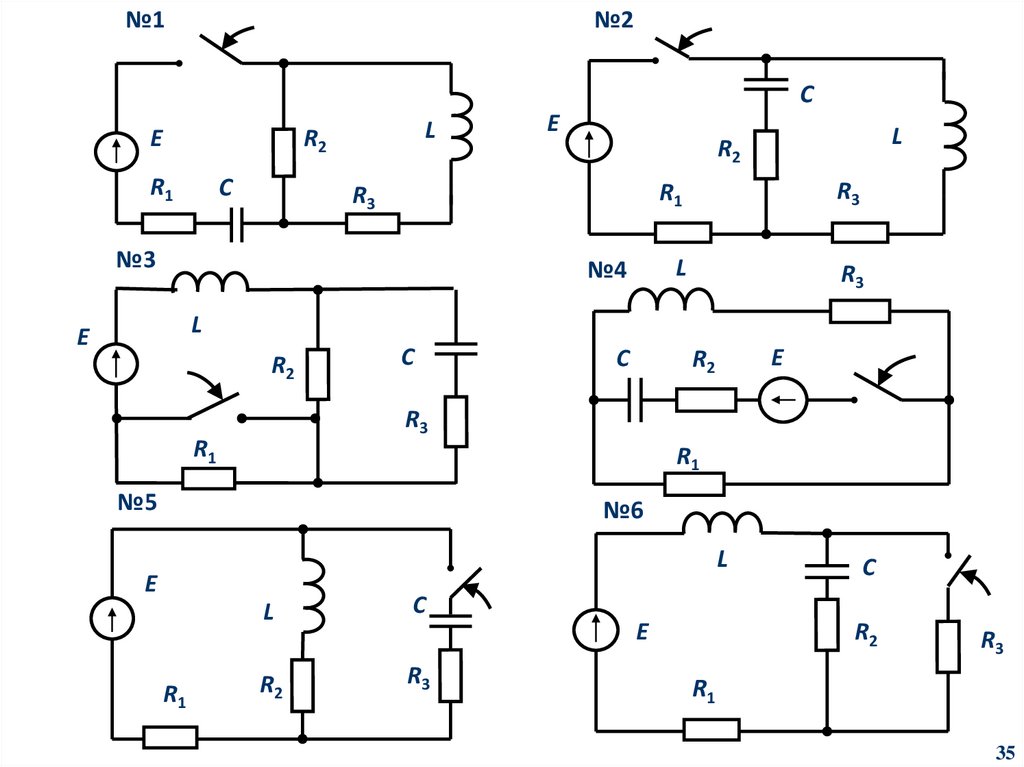
третья цифра —
соответствует номеру схемы
32
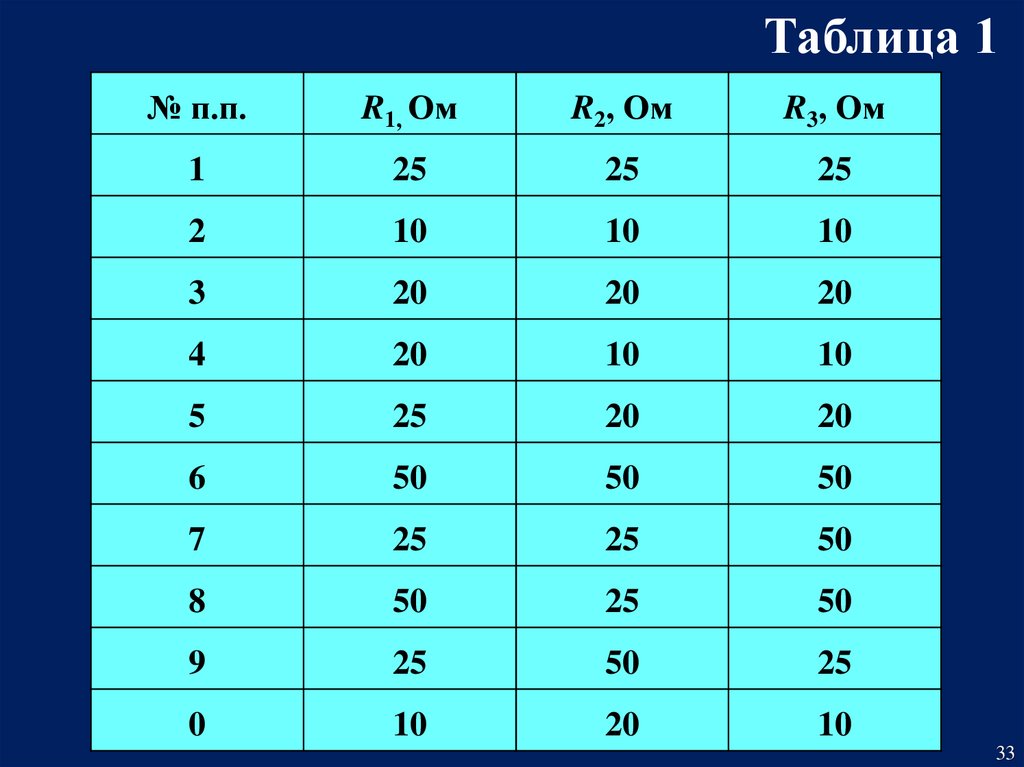
33.
Таблица 1№ п.п.
R1, Ом
R2, Ом
R3, Ом
1
25
25
25
2
10
10
10
3
20
20
20
4
20
10
10
5
25
20
20
6
50
50
50
7
25
25
50
8
50
25
50
9
25
50
25
0
10
20
10
33
34.
Таблица 2№ п.п.
C, мкФ
E, B
L, мГ
1
100
125
100
2
50
110
150
3
80
120
80
4
200
200
200
5
170
250
170
6
150
150
180
7
40
500
120
8
60
350
110
9
125
550
150
0
130
280
125
34
35.
№1№2
C
E
L
R2
R1
C
E
R3
№3
L
R2
№4
R1
R3
L
R3
L
E
R2
C
C
E
R2
R3
R1
R1
№5
№6
L
E
L
R1
R2
C
C
E
R3
R2
R3
R1
35
36.
№8№7
LL
E
L
C
R1
R2
E
R2
R3
R1
R3
№9
C
R3
R3
№0
C
L
E
L
E
R2
R2
R3
R1
C
R3
R1
36
37.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ«ДОНСКОЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА
«ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА»
Расчётно-графическая работа №2
по теме:
«Расчёт переходных процессов в линейных
электрических цепях»
Вариант: 1 - 3 - 8
Выполнил студент группы ЭЛ2-1
Сидоров В.П.
38.
ФункцияПроверил: доцент ВИНОКУРОВ М.Р.
ТАБЛИЦА ОТВЕТОВ
Вид решения
Значения
функции
при при при
t = 0─ t = 0 t = ∞
i1 (t) =
i2 (t) =
i3 (t) =
uL (t)=
uC (t) =
г. Ростов – на – Дону
20__ – 20 __ учебный год
38
39.
Содержание работы:1. Рассчитать все переходные токи
цепи и переходные напряжения на
конденсаторе и на катушке
индуктивности классическим методом.
2. Составить систему дифференциальных
уравнений для метода переменных
состояния и рассчитать ток в катушке
индуктивности и напряжение на
конденсаторе при помощи
специализированной программы.
39
40.
3. Построить временныезависимости в одной системе
координат по результатам,
полученными двумя методами
для:
тока в ветви с индуктивностью;
напряжения на конденсаторе.
4. Результаты расчетов занести в
таблицу ответов на титульном листе.
40
41.
В качестве примера рассмотримвариант задачи со следующими
исходными данными:
R1 = 20 Ом; R2 = 30 Ом;
R3 = 10 Ом;
L = 0,125 Гн; С = 0,00013 Ф;
Е = 100 В
41
42.
i3(t)С
i1(t)
i2(t)
Е
R1
uL(t)
uC (t)
R2
R3
L
42
43.
1. Расчёт всехпереходных токов цепи
и переходных
напряжений на
конденсаторе и на
катушке индуктивности
классическим методом
43
44.
РЕШЕНИЕСоставим систему дифференциальных
уравнений для мгновенных значений токов
и напряжений по законам Кирхгофа для
режима после коммутации:
i3(t)
i1(t)
Е
R1
i2(t)
С
R2
L
R3
Уравнение (2) принимаем за БАЗОВОЕ
44
45.
Cформируем неоднородноедифференциальное уравнение
относительно переменной uC (t)
Для этого установим связь всех
переменных уравнения с
переменной uC (t)
45
46.
Выразим ток i2 из уравнения (3)С учётом того, что
46
47.
4748.
4849.
Выразим напряжение накатушке индуктивности:
49
50.
5051.
Группируем полученное уравнение иформируем неоднородное
дифференциальное
уравнение 2 порядка относительно
напряжения на конденсаторе:
С учётом числовых значений уравнение
принимает вид:
51
52.
илиПолное решение для
напряжения на конденсаторе:
52
53.
Расчёт принуждённойсоставляющей
Так как источник ЭДС – постоянный
во времени, то
Исходное дифференциальное
уравнение в этом случае
принимает вид:
53
54.
5455.
Расчёт свободной составляющейПреобразуем исходное неоднородное
дифференциальное уравнение к однородному
Алгебраизируем однородное
дифференциальное
уравнение:
55
56.
Решение квадратного уравнения вида:56
57.
5758.
Комплексносопряжённые корниуказывают на
колебательный или
периодический
затухающий
переходный режим
58
59.
Вид решения для свободной составляющейи полное решение для uc
Полученное решение для нулевого
момента времени ( t = 0) :
59
60.
В качестве такого уравнения можетбыть использовано уравнение для
тока, протекающего в ветви с
конденсатором:
60
61.
Для нулевого момента времени ( t = 0) :61
62.
Система уравнений, состоящая изуравнений (4) и (5), позволяет
определить постоянные
интегрирования А и γ :
62
63.
Если корни дифференциальногоуравнения отрицательные,
вещественные и разные, то такой
переходный процесс называется
апериодическим
НАПРИМЕР:
63
64.
Вид решения для свободнойсоставляющей и полное решение для uc
в данном случае имеют вид:
Для нулевого момента времени( t = 0):
64
65.
В качестве такого уравнения и вданном случае может быть
использовано уравнение для тока,
протекающего в ветви с
конденсатором:
65
66.
Для нулевого момента времени ( t = 0) :66
67.
6768.
Для совместного решенияэтих уравнений
[ как и уравнений (4) и (5)]
необходимо определить значения
величин в левой части уравнений
т.е.
68
69.
6970.
7071.
Выполним расчёт заданной схемы докоммутации
( для момента времени t = 0_ )
i3(0_
i3(t))
(0_ )
ii11(t)
Е
R1
i1(0_ ) = 0;
i2(0_ ) = 0;
i3(0_ ) = 0;
uС(0_L) = 0;
uL(0_ ) = 0
(0_ )
i22(t)
R2
С
uC(0_ )
R3
71
72.
В данном случае искомыенезависимые начальные условия
являются нулевыми, т.е.:
uC(0_ ) = 0; i1(0_ ) = 0
В соответствии с законами
коммутации:
uC (0) = 0; i1(0) = 0
72
73.
Исходная система уравнений для моментавремени t = 0 может быть преобразована с
учётом независимых начальных условий:
0
73
74.
Из уравнения (1)Из уравнения (3)
74
75.
Из уравнения (1):i2 (0) = – i3(0) = 0
Из уравнения (2):
75
76.
По результатам расчётаприведённой схемы в момент
коммутации (t = 0 )
получаем следующие результаты:
i1(0) =
i2(0) =
i3(0) =
uС(0) =
uL (0) =
0;
0;
0;
0;
100 В
76
77.
Уравнения (4) и (5) могут быть теперь решенысовместно:
0 = 60 + A × sin γ
0 = – 0,0268 × A × sinγ
+ 0,02412 × A × cosγ
77
78.
0 = – 0,0268×A×
sinγ
+ 0,02412 ×A×
cosγ
0 = 1,608 – 1,447ctg γ
γ = arctg ( 0,9 ) = 42º
78
79.
7980.
8081.
8182.
8283.
8384.
8485.
2. Вывод системыдифференциальных уравнений
для метода переменных
состояния и расчёт тока в
катушке индуктивности и
напряжения на конденсаторе
при помощи
специализированной
программы.
85
86.
В основу программы положен метод Рунге – Кутта —метод численного решения уравнения состояния,
при котором
разбивается на « n » малых участков
на каждом из которых значение
переменной определяется с помощью
линейной комбинации некоторых
вспомогательных функций с
постоянными коэффициентами.
86
87.
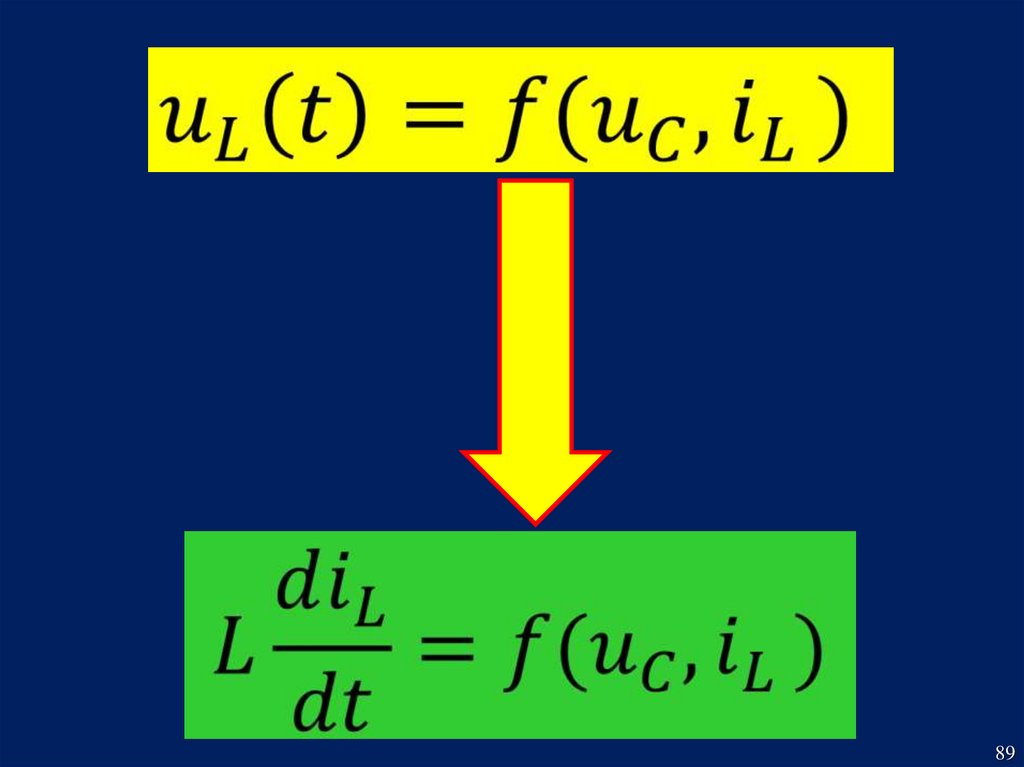
Достаточно получитьследующие функциональные
зависимости:
87
88.
8889.
8990.
РЕШЕНИЕ90
91.
Выразим ток i2 из уравнения (1)Подставим ток i2 в уравнение (3)
91
92.
9293.
k – номер шага итерацииk = 0, 1, 2, ……. n
93
94.
После подстановки числовыхзначений получим:
94
95.
9596.
9697.
9798.
9899.
После подстановки числовыхзначений получим:
99
100.
С помощью специализированной программывыполняется совместное решение
полученных итерационных уравнений:
При следующих начальных условиях:
100
101.
Порядок обращения к программеЗАДАЧА №2
ВАРИАНТ №
Метод переменных состояния
Х-Х-Х
0
0
A =
D=
800
В = -192,3
E=
-6
С = 5769,2
F=
-220
0
В
А
t п.п. = 2,425E-02
Δt =
6,062E-05
СЕК
СЕК
101
102.
3. Построение временныхзависимостей
напряжения на конденсаторе
и тока в ветви с
индуктивностью в одной
системе координат по
результатам, полученным
двумя методами
102
103.
Построение графических зависимостей по результатам расчётаклассическим методом (программа КПП)
S = 60
T = -89,70
K= 2
t п.п.
Δt
C= -206,2
L= 2,892
D = 185,5
N= -43,8
=
2,4248E-02 СЕК
Т' =
3,3854E-02 СЕК
=
2,425E-04
R= 42
140
СЕК
103
104.
При возникновении апериодическогопереходного процесса (АПП) следует
обратиться к соответствующей программе и
ввести значения требуемых коэффициентов
Построение графических зависимостей по результатам расчёта
классическим методом (программа АПП)
L= 200
M=
500,00
N = -700
P 1= -200,0
S=
3
T=
5
R=
-8
P 2= -500,0
104
105.
Зависимость напряжения на конденсаторе (В) в функции времени (мсек)70,0
60,0
50,0
40,0
30,0
20,0
10,0
0,0
0,0
5,0
10,0
15,0
20,0
25,0
30,0
-10,0
105
106.
Зависимость тока в ветви с индуктивностью (А) в функции времени (мсек)2,50
2,00
1,50
1,00
0,50
0,00
0,0
5,0
10,0
15,0
20,0
25,0
30,0
-0,50
106
107.
Функция4. Таблица
ответов
Вид решения
Значения
функции
при при при
t = 0─ t = 0 t = ∞
i1(t)=
0
0
2
i2(t)=
0
0
2
i3(t)=
uL (t)=
0
0
0
0
100
0
uC (t) =
0
0
60
107











































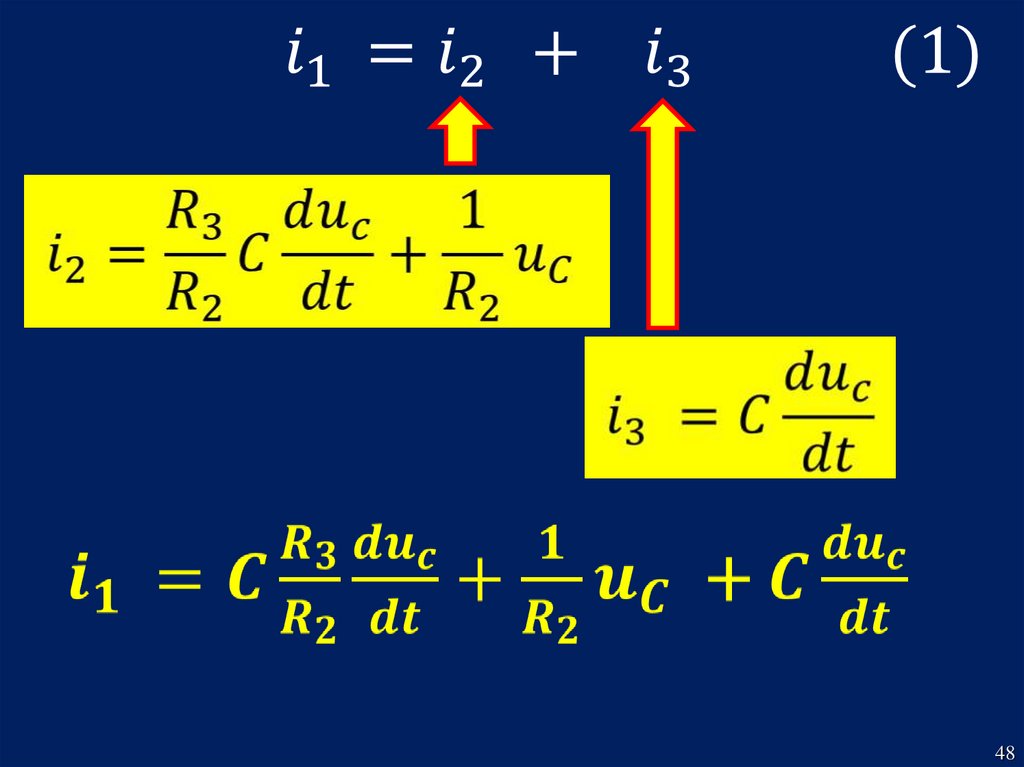


























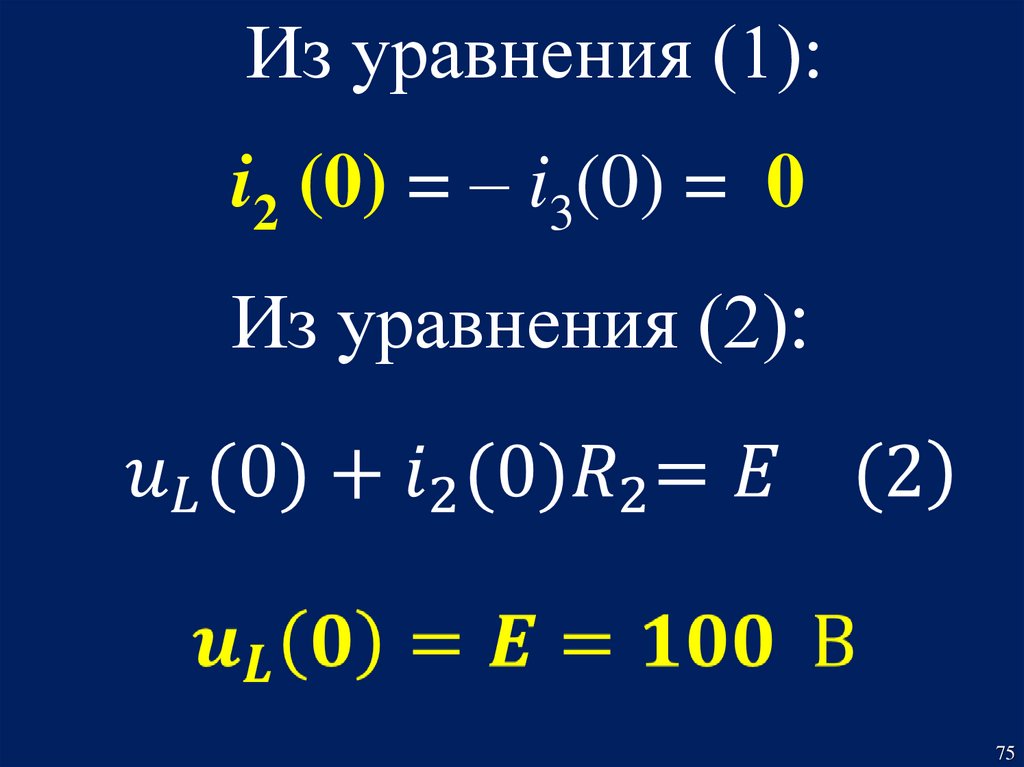


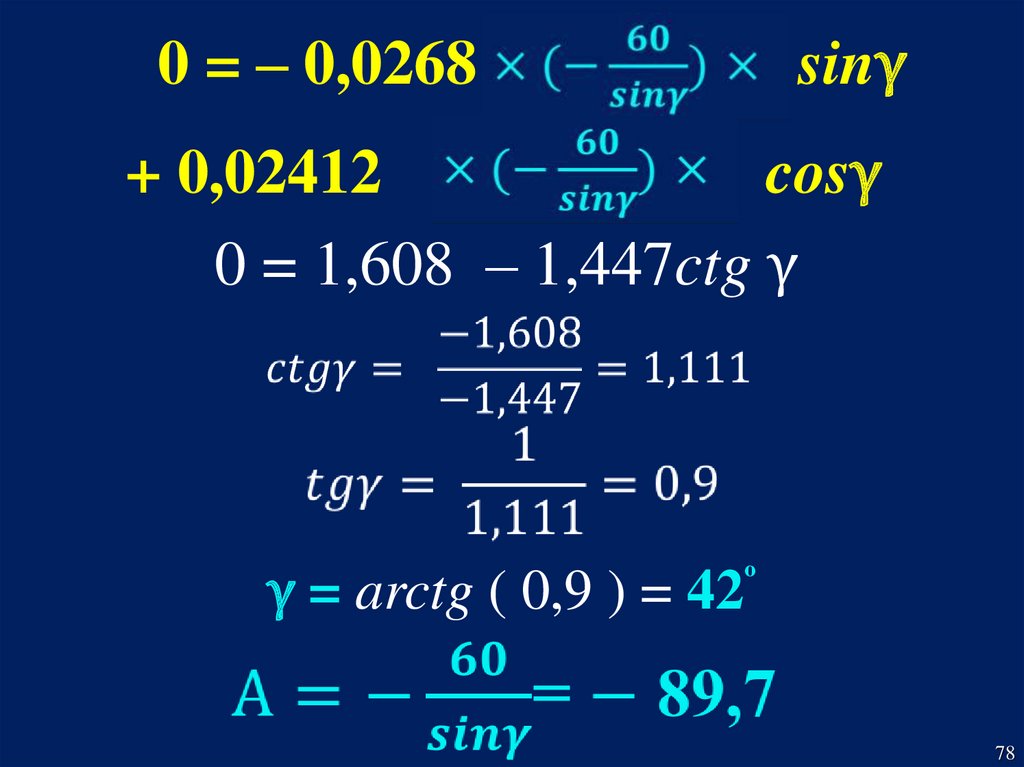




























 physics
physics








