Similar presentations:
Переходные процессы в линейных электрических цепях
1.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ ВЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ
ЦЕПЯХ
Теоретические основы
электротехники
1
2.
ПЛАН1. Понятие переходного процесса.
2. Законы коммутации.
3. Независимые и зависимые начальные условия.
4. Характеристическое уравнение электрической цепи.
5. Классический метод расчета переходных процессов.
6. Переходные процессы в RL-цепях постоянного тока.
7. Заряд и разряд конденсатора.
2
3.
ПОНЯТИЕ ПЕРЕХОДНОГОПРОЦЕССА
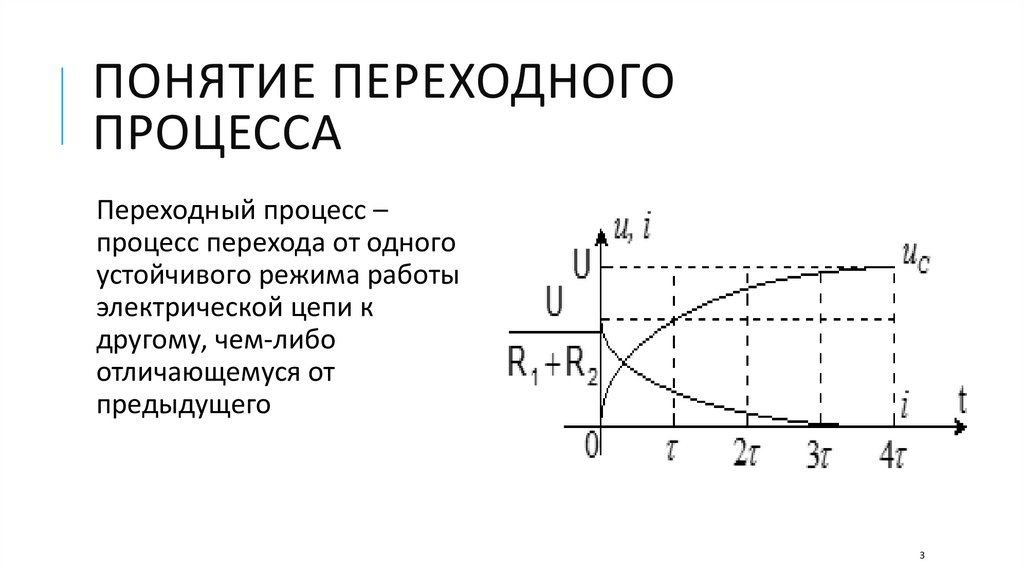
Переходный процесс –
процесс перехода от одного
устойчивого режима работы
электрической цепи к
другому, чем-либо
отличающемуся от
предыдущего
3
4.
ПОНЯТИЕ ПЕРЕХОДНОГОПРОЦЕССА
Возникает вследствие коммутации:
включения или отключения пассивных или активных
ветвей,
коротких замыканий отдельных участков,
различного рода переключений,
внезапного изменения параметров и т.д.
Заканчивается спустя некоторое время после
коммутации
4
5.
ПОНЯТИЕ ПЕРЕХОДНОГОПРОЦЕССА
Коммутация в переходных процессах — мгновенное
изменение параметров электрической цепи
Коммутация — процессы, происходящие в первый момент
времени после переключения в электрических цепях при
замыканиях и размыканиях различных участков цепи
5
6.
ПОНЯТИЕ ПЕРЕХОДНОГОПРОЦЕССА
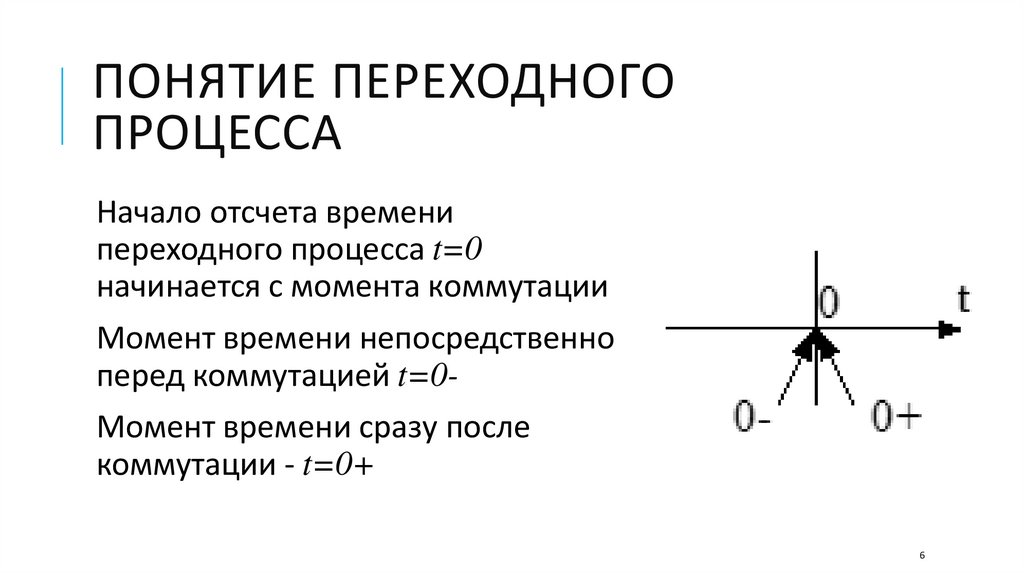
Начало отсчета времени
переходного процесса t=0
начинается с момента коммутации
Момент времени непосредственно
перед коммутацией t=0Момент времени сразу после
коммутации - t=0+
6
7.
ПОНЯТИЕ ПЕРЕХОДНОГОПРОЦЕССА
Цель расчета – в
определении законов
изменения токов и
напряжений во время
коммутации
U U
i e
R R
R
t
L
u C U Ue
t
R1 R2 C
7
8.
ЗАКОНЫ КОММУТАЦИИ.ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
Ток через индуктивность
непосредственно до
коммутации равен току через ту
же индуктивность
непосредственно после
коммутации
iL (0 ) iL (0 )
Ток на индуктивности не может
изменяться скачком
8
9.
ЗАКОНЫ КОММУТАЦИИ.ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
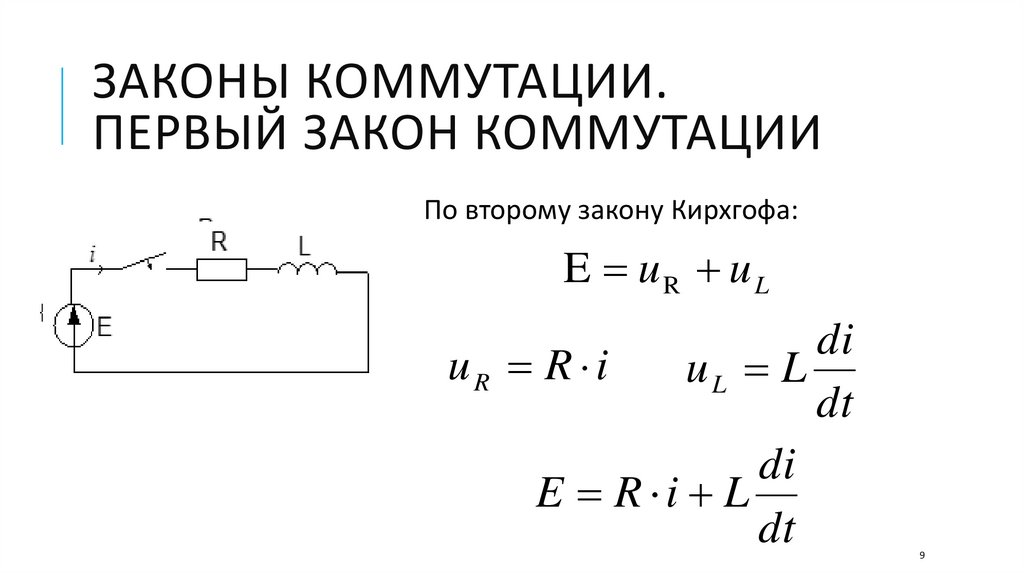
По второму закону Кирхгофа:
E uR u L
di
uR R i
uL L
dt
di
E R i L
dt
9
10.
ЗАКОНЫ КОММУТАЦИИ.ПЕРВЫЙ ЗАКОН КОММУТАЦИИ
Пусть ток во время переходного процесса изменится скачком, т.е. за
время t 0 ток изменится на конечную величину
i( 0 )-i( 0-) Δi
di
i
i
lim
dt t 0 t
t
E R i
di
L
dt
E – конечная величина, следовательно, не соблюдается II
закон Кирхгофа, и предположение о том, что ток,
протекающий через индуктивность, может измениться
скачком, неверно
10
11.
ЗАКОНЫ КОММУТАЦИИ.ВТОРОЙ ЗАКОН КОММУТАЦИИ
Напряжение на емкости
непосредственно до
коммутации равно напряжению
на той же емкости
непосредственно после
коммутации,
uC (0 ) uC (0 )
Напряжение на емкости не
может измениться скачком
11
12.
ЗАКОНЫ КОММУТАЦИИ.ВТОРОЙ ЗАКОН КОММУТАЦИИ
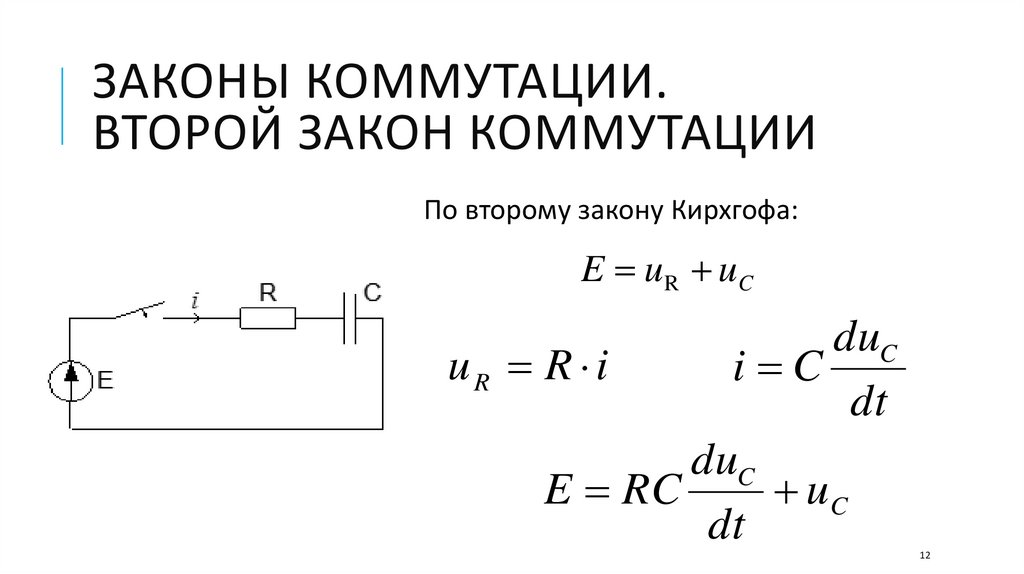
По второму закону Кирхгофа:
E u R uC
duC
uR R i
i C
dt
duC
E RC
uC
dt
12
13.
ЗАКОНЫ КОММУТАЦИИ.ВТОРОЙ ЗАКОН КОММУТАЦИИ
Пусть во время переходного процесса падение напряжения на
конденсаторе изменится скачком, т.е. за время t 0 напряжение
изменится на конечную величину
C
C
C
u (0 ) u (0 ) u
duC
uC
du
uC
C
lim
C
dt
t
t
dt
t 0
E R C uC
E – конечная величина, следовательно, не соблюдается II
закон Кирхгофа, и предположение о том, что падение
напряжения на конденсаторе может измениться
скачком, неверно
13
14.
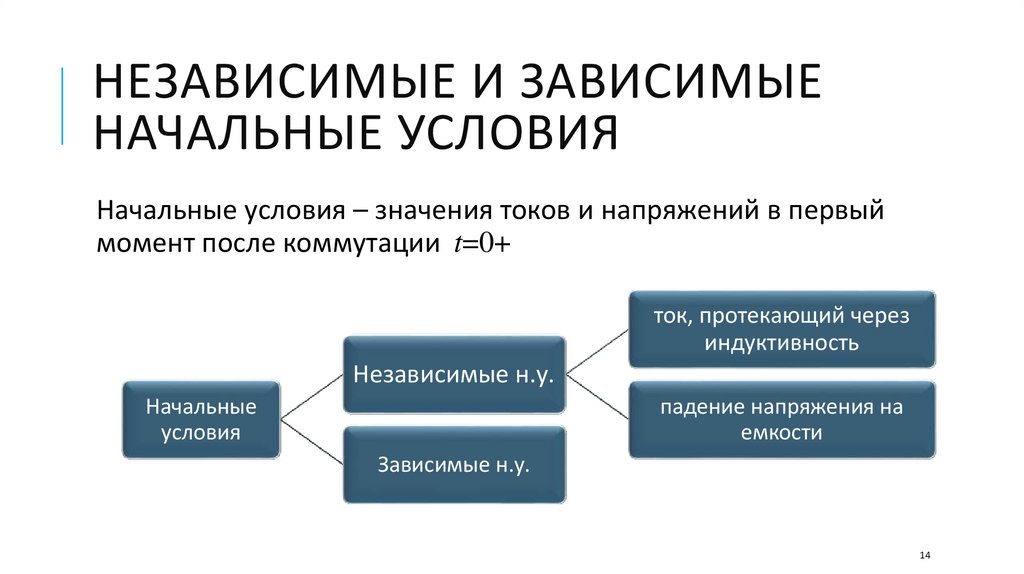
НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕНАЧАЛЬНЫЕ УСЛОВИЯ
Начальные условия – значения токов и напряжений в первый
момент после коммутации t=0+
ток, протекающий через
индуктивность
Независимые н.у.
Начальные
условия
падение напряжения на
емкости
Зависимые н.у.
14
15.
НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕНАЧАЛЬНЫЕ УСЛОВИЯ
Независимые начальные условия определяются из законов
коммутации:
i L (0 ) iL (0) iL (0 )
uC (0 ) uC (0) uC (0 )
Зависимые начальные условия определяются из законов
Кирхгофа и известных независимых начальных условий
15
16.
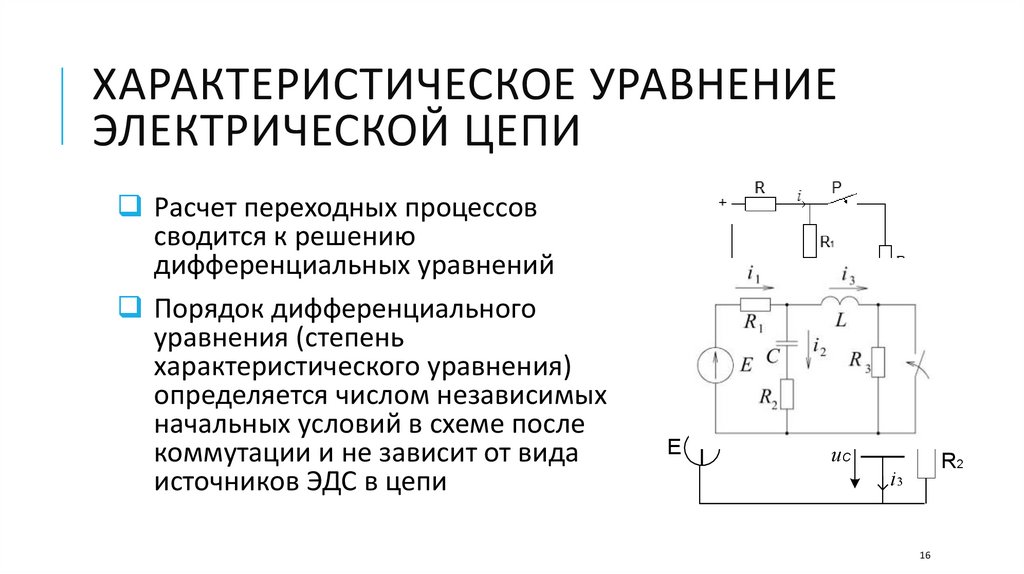
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Расчет переходных процессов
сводится к решению
дифференциальных уравнений
Порядок дифференциального
уравнения (степень
характеристического уравнения)
определяется числом независимых
начальных условий в схеме после
коммутации и не зависит от вида
источников ЭДС в цепи
R1 i1
E
R3
uC
i2
C
R2
i3
16
17.
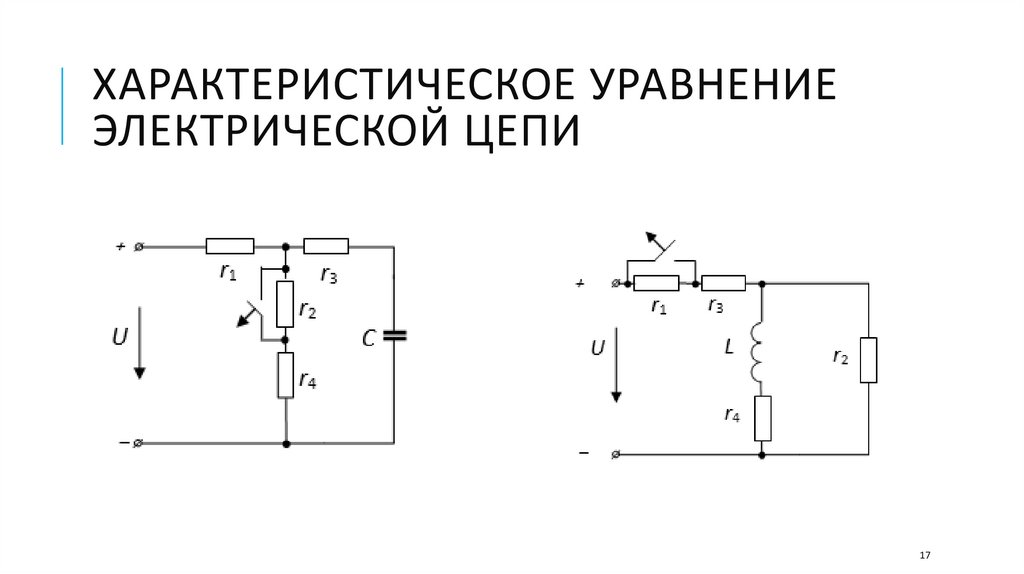
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕЭЛЕКТРИЧЕСКОЙ ЦЕПИ
17
18.
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕЭЛЕКТРИЧЕСКОЙ ЦЕПИ
1. Записывается входное сопротивление переменному току
электрической цепи после коммутации
Z ( j )
2. Заменяется в нем
на р. Получается
j
характеристическое уравнение
Z ( p) 0
3. Находятся корни этого характеристического уравнения p.
[p]=с-1.
18
19.
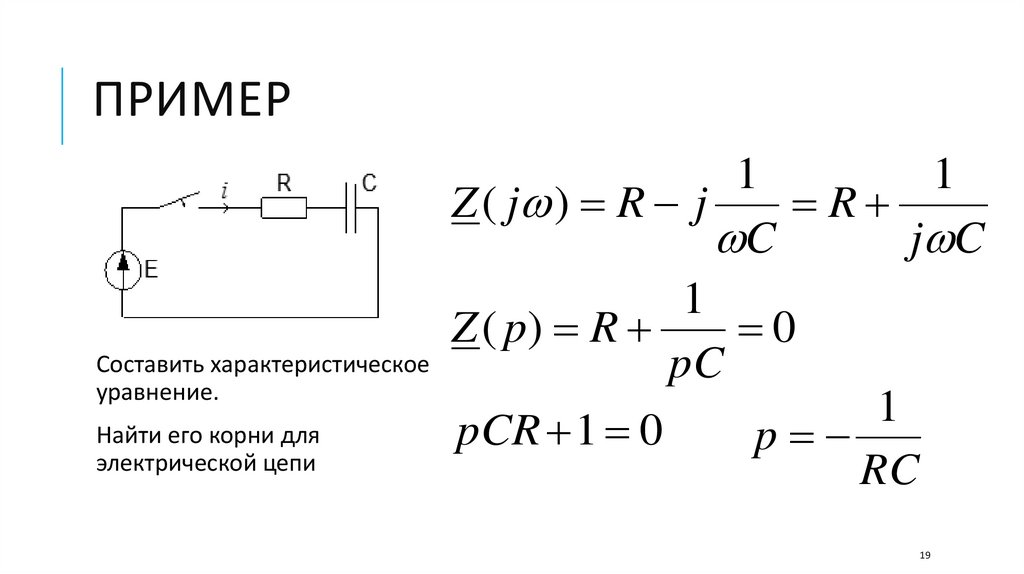
ПРИМЕРСоставить характеристическое
уравнение.
Найти его корни для
электрической цепи
1
1
Z ( j ) R j
R
C
j C
1
Z ( p) R
0
pC
1
pCR 1 0
p
RC
19
20.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТАПЕРЕХОДНЫХ ПРОЦЕССОВ
1. Для цепи после коммутации составить систему дифференциальных
уравнений по I и II законам Кирхгофа.
2. Определить независимые начальные условия (uC и iL) из расчета
режима цепи до коммутации с применением законов коммутации.
3. Записать искомые величины в виде суммы принужденных и
свободных составляющих.
4. Найти принужденные составляющие, рассчитав установившийся
режим цепи после коммутации.
20
21.
КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТАПЕРЕХОДНЫХ ПРОЦЕССОВ
5. Составить характеристическое уравнение и вычислить его корни.
6. В зависимости от вида корней характеристического уравнения
записать свободные составляющие и искомые решения в общем
виде.
7. Для определения постоянных интегрирования записать искомые
величины, их производные и систему дифференциальных уравнений
для момента t=0.
8. Подставить вычисленные постоянные интегрирования в искомые
решения.
9. Построить графики изменения токов и напряжений во время
переходного процесса.
21
22.
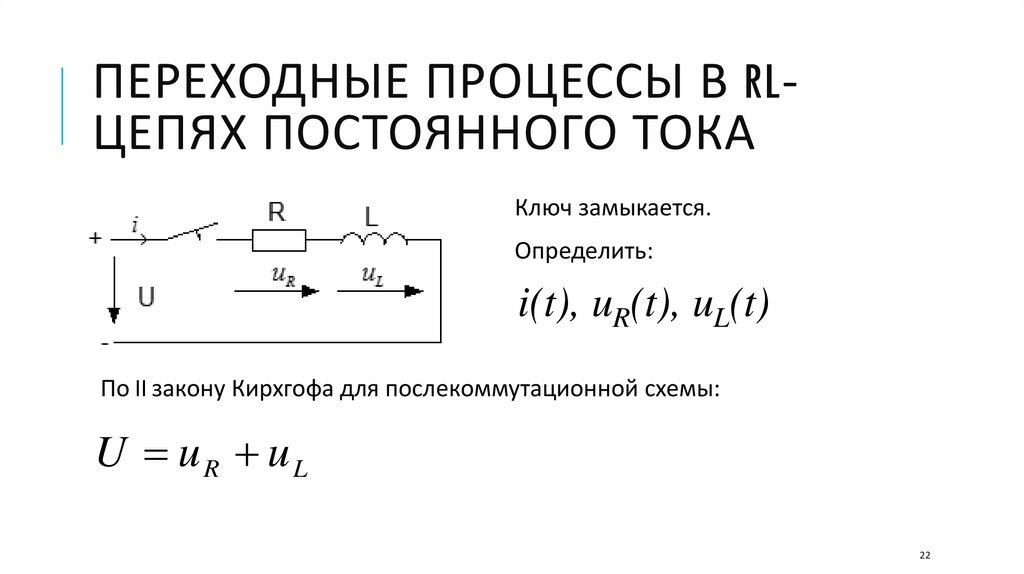
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАКлюч замыкается.
Определить:
i(t), uR(t), uL(t)
По II закону Кирхгофа для послекоммутационной схемы:
U uR uL
22
23.
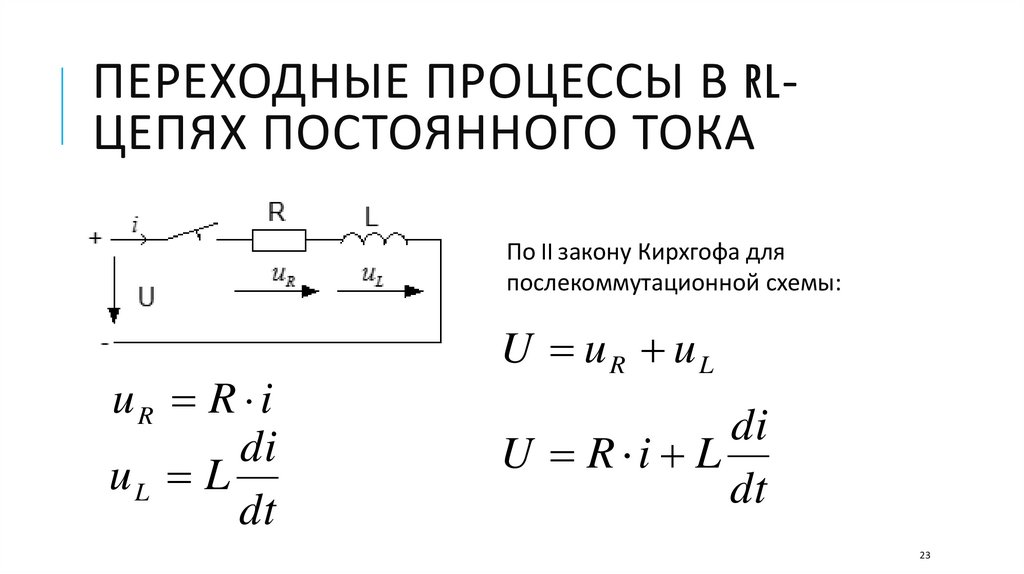
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАПо II закону Кирхгофа для
послекоммутационной схемы:
uR R i
di
uL L
dt
U uR uL
di
U R i L
dt
23
24.
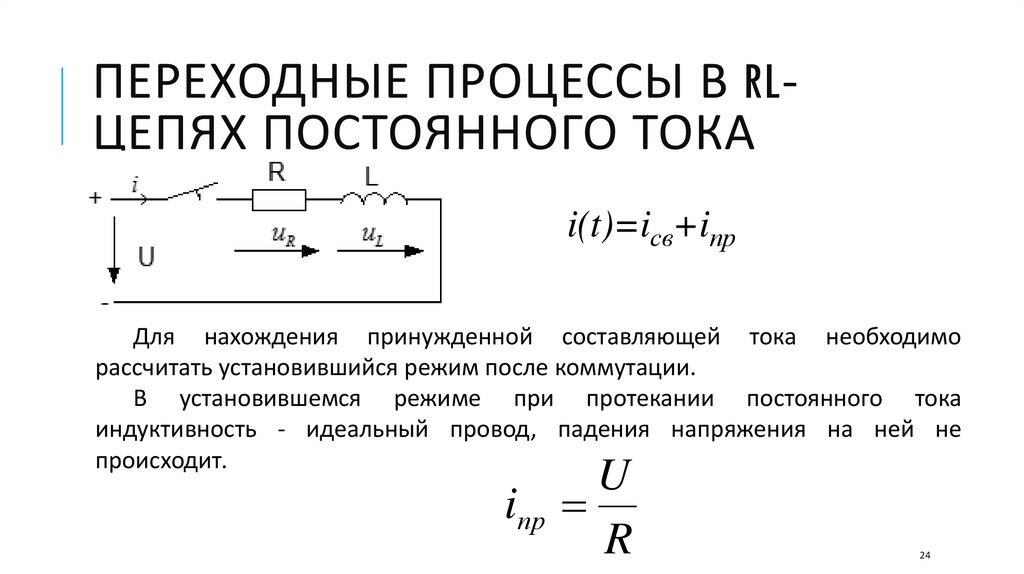
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАi(t)=iсв+iпр
Для нахождения принужденной составляющей тока необходимо
рассчитать установившийся режим после коммутации.
В установившемся режиме при протекании постоянного тока
индуктивность - идеальный провод, падения напряжения на ней не
происходит.
U
iпр
R
24
25.
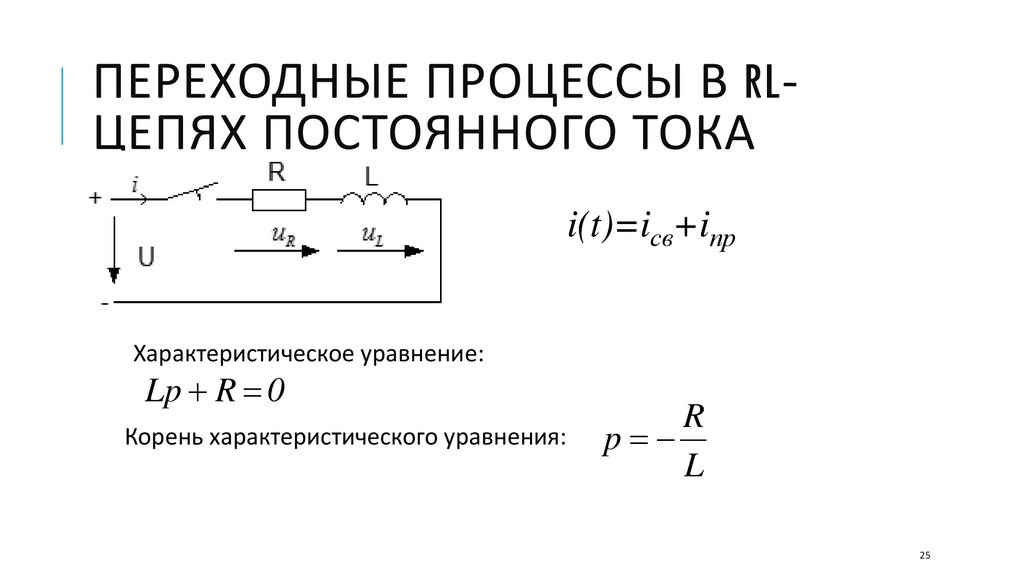
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАi(t)=iсв+iпр
Характеристическое уравнение:
Lp R 0
Корень характеристического уравнения:
R
p
L
25
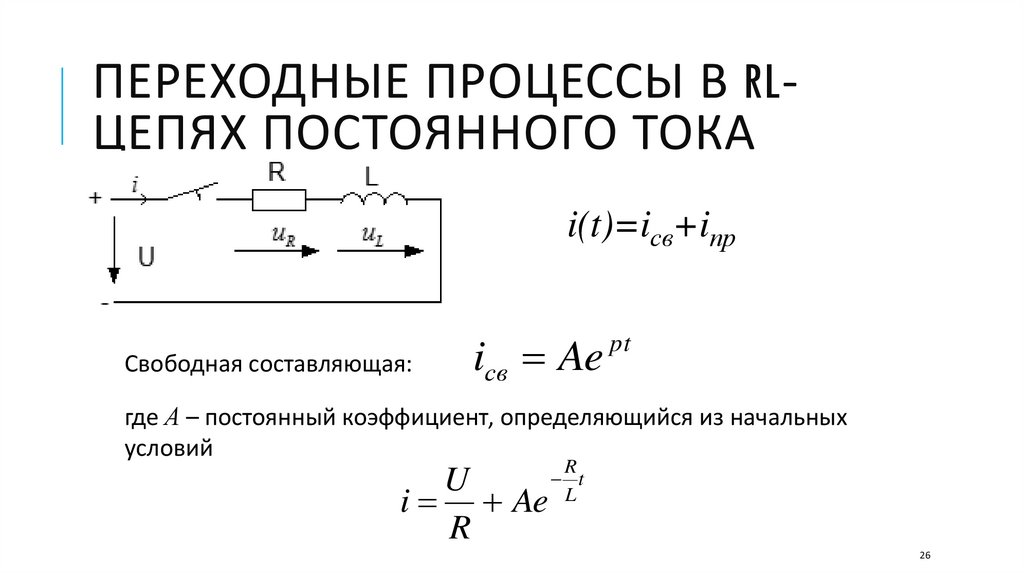
26.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАi(t)=iсв+iпр
Свободная составляющая:
iсв Ae
pt
где А – постоянный коэффициент, определяющийся из начальных
условий
U
i Ae
R
R
t
L
26
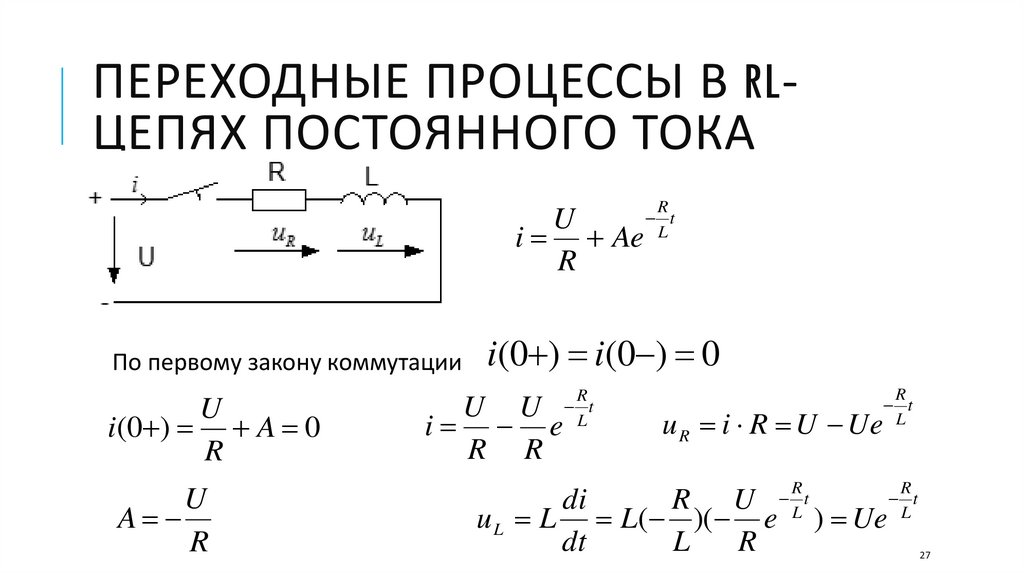
27.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАR
t
U
i Ae L
R
По первому закону коммутации
U
i(0 ) A 0
R
U
A
R
i(0 ) i(0 ) 0
U U
i e
R R
R
t
L
u R i R U Ue
di
R U
u L L L( )( e
dt
L
R
R
t
L
R
t
L
) Ue
R
t
L
27
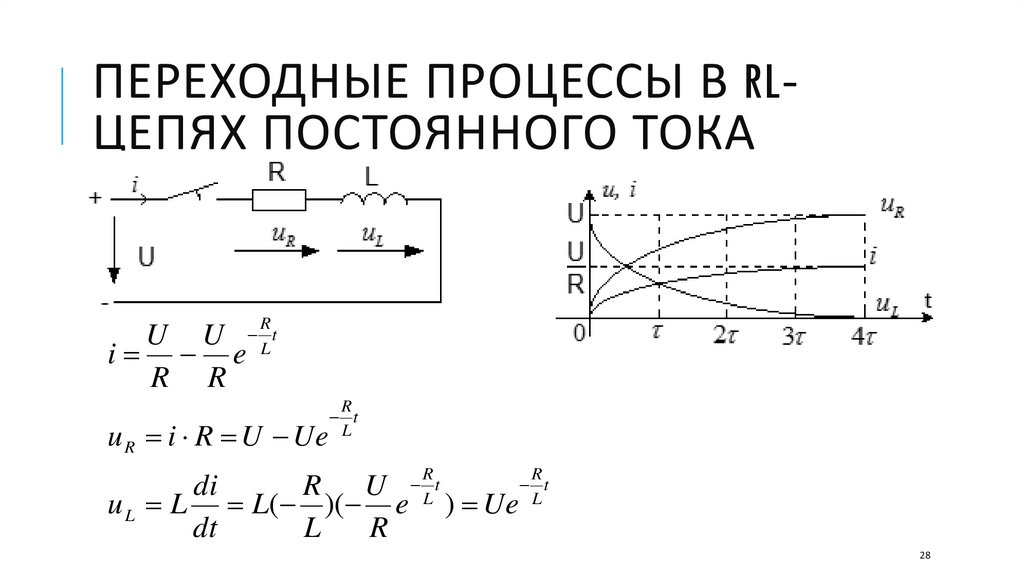
28.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКАR
U U Lt
i e
R R
u R i R U Ue
R
t
L
di
R U
u L L L( )( e
dt
L
R
R
t
L
) Ue
R
t
L
28
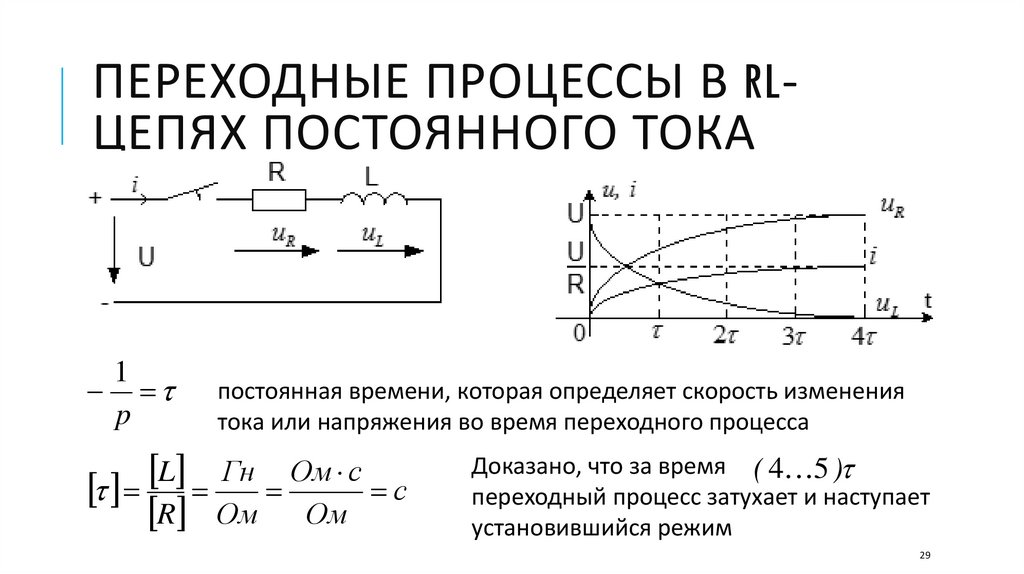
29.
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В RLЦЕПЯХ ПОСТОЯННОГО ТОКА1
p
постоянная времени, которая определяет скорость изменения
тока или напряжения во время переходного процесса
L Гн Ом с
с
R Ом Ом
Доказано, что за время ( 4 5 )
переходный процесс затухает и наступает
установившийся режим
29
30.
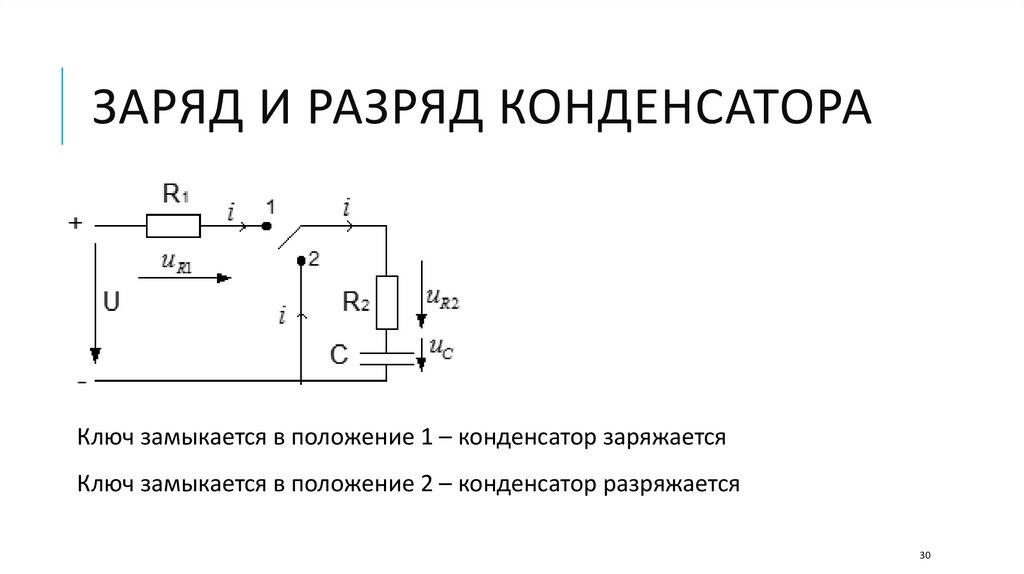
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРАКлюч замыкается в положение 1 – конденсатор заряжается
Ключ замыкается в положение 2 – конденсатор разряжается
30
31.
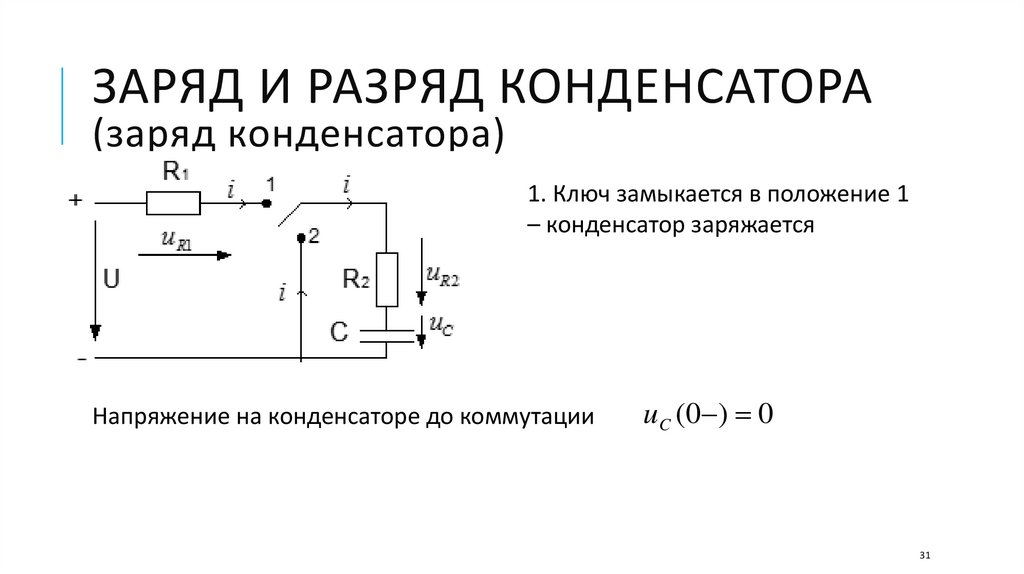
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(заряд конденсатора)
1. Ключ замыкается в положение 1
– конденсатор заряжается
Напряжение на конденсаторе до коммутации
u C (0 ) 0
31
32.
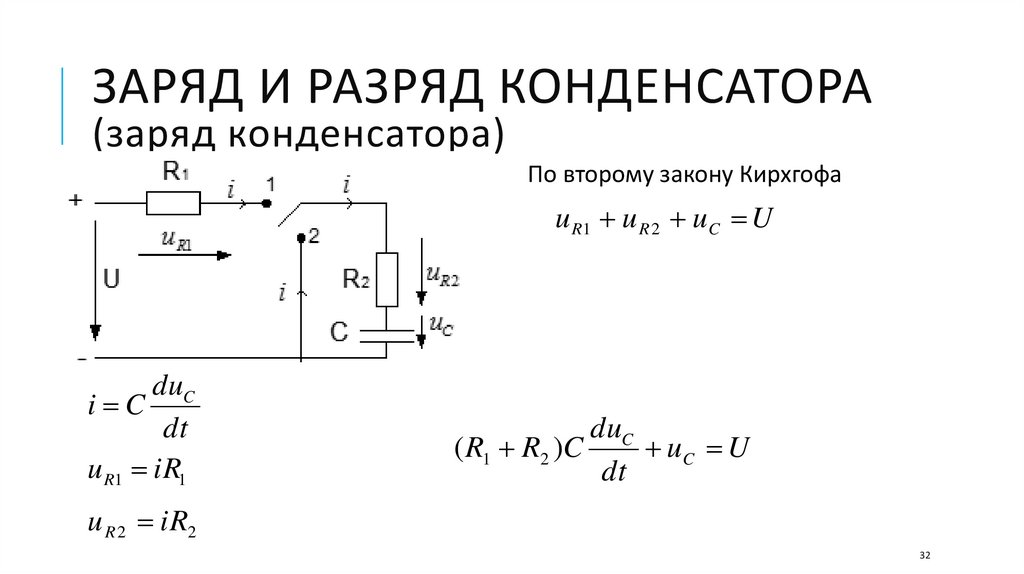
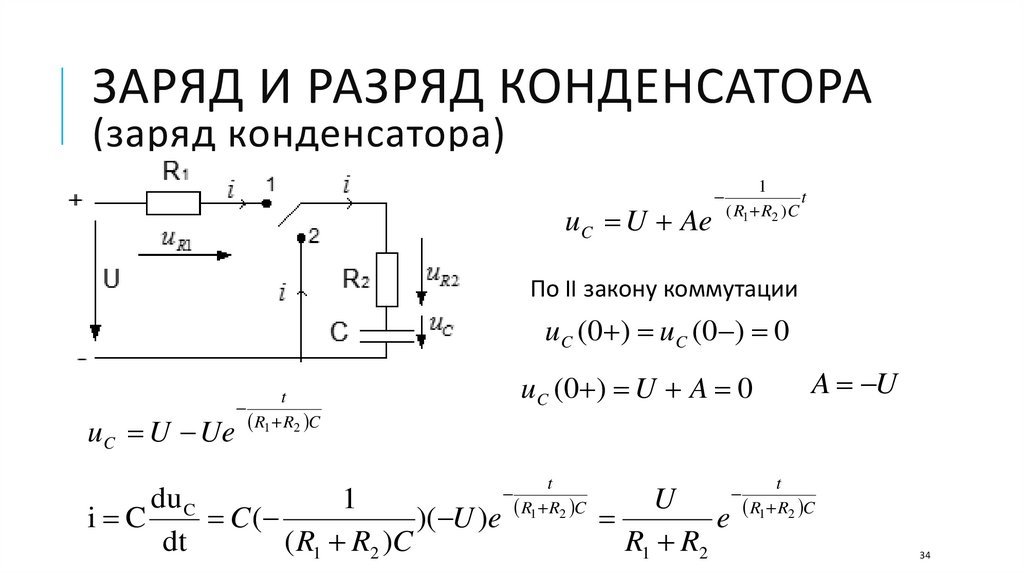
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(заряд конденсатора)
По второму закону Кирхгофа
u R1 u R 2 uC U
duC
i C
dt
u R1 iR1
duC
( R1 R2 )C
uC U
dt
u R 2 iR2
32
33.
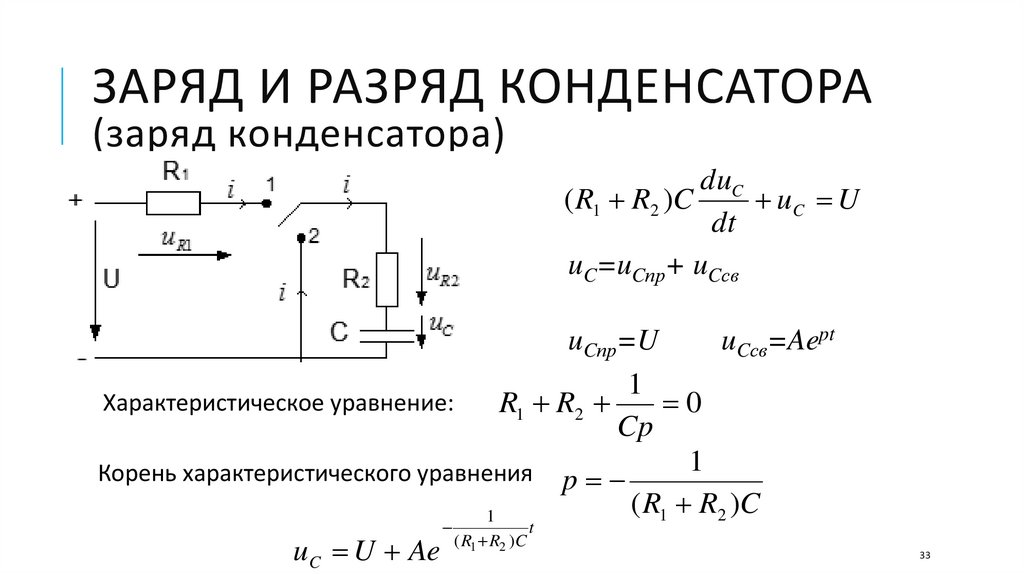
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(заряд конденсатора)
duC
( R1 R2 )C
uC U
dt
uC=uCпр+ uCсв
uCпр=U
uCсв=Aept
1
Характеристическое уравнение:
R1 R2
0
Cp
1
Корень характеристического уравнения p
( R1 R2 )C
1
uC U Ae
( R1 R2 ) C
t
33
34.
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(заряд конденсатора)
uC U Ae
1
t
( R1 R2 ) C
По II закону коммутации
u C ( 0 ) u C ( 0 ) 0
u C U Ue
u C (0 ) U A 0
t
R1 R2 C
du C
1
i C
C (
)( U )e
dt
( R1 R2 )C
t
R1 R2 C
U
e
R1 R2
A U
t
R1 R2 C
34
35.
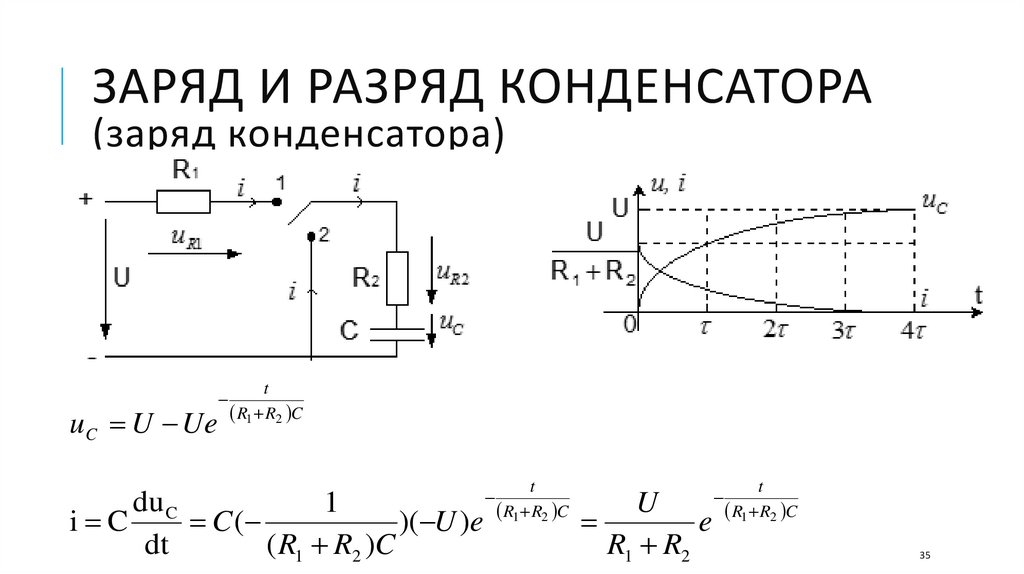
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(заряд конденсатора)
u C U Ue
t
R1 R2 C
du C
1
i C
C (
)( U )e
dt
( R1 R2 )C
t
R1 R2 C
U
e
R1 R2
t
R1 R2 C
35
36.
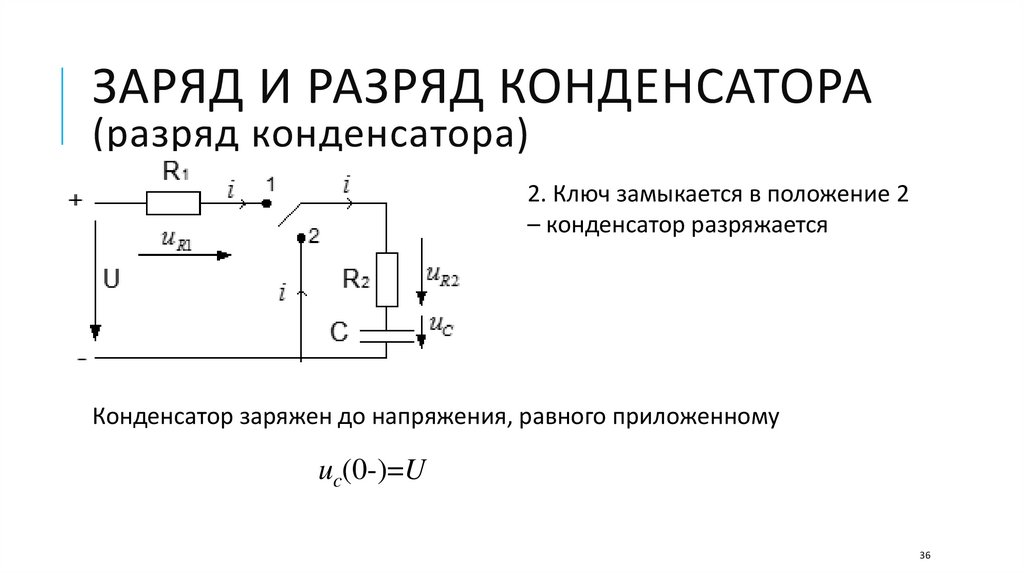
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(разряд конденсатора)
2. Ключ замыкается в положение 2
– конденсатор разряжается
Конденсатор заряжен до напряжения, равного приложенному
uc(0-)=U
36
37.
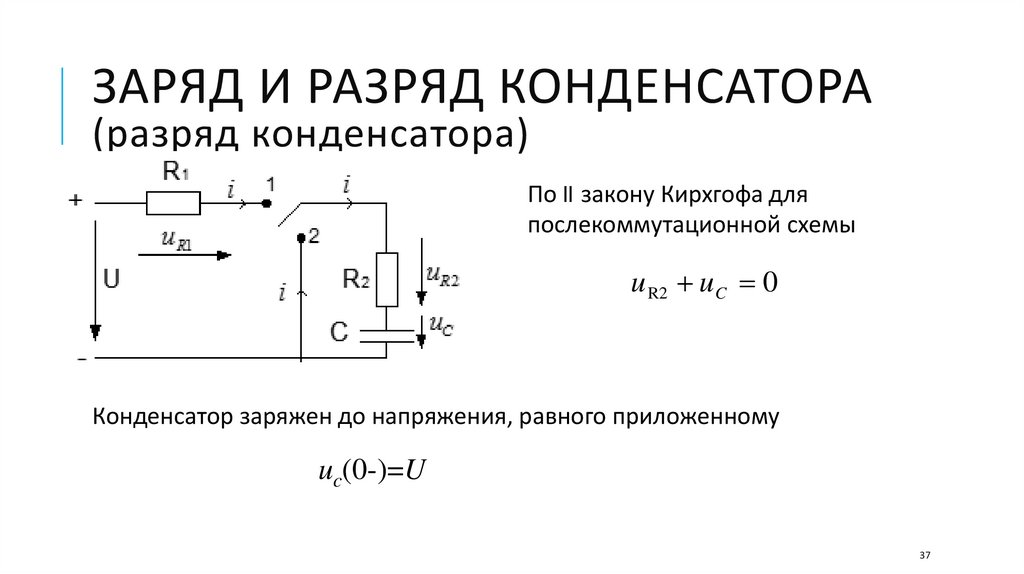
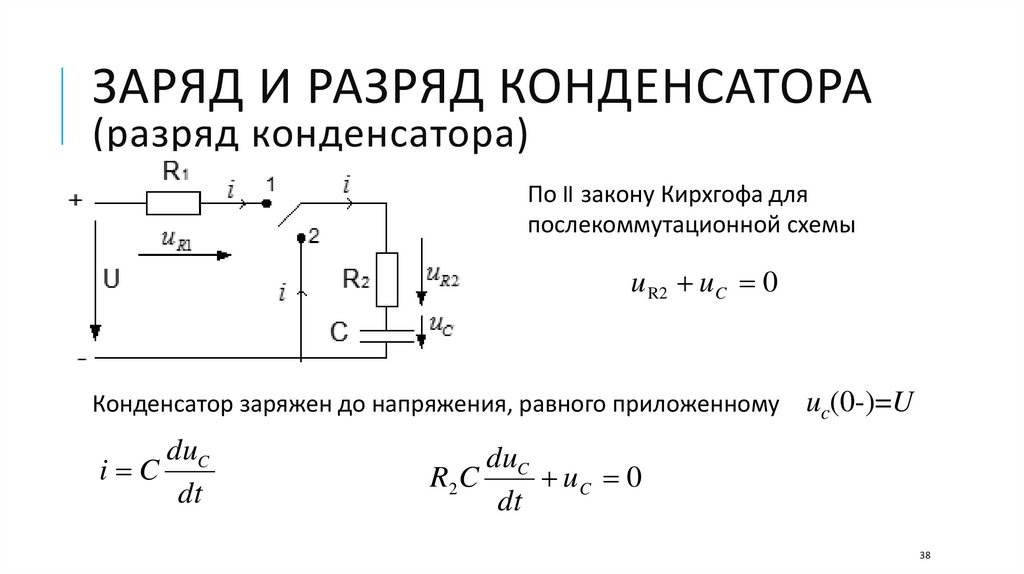
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(разряд конденсатора)
По II закону Кирхгофа для
послекоммутационной схемы
u R2 u C 0
Конденсатор заряжен до напряжения, равного приложенному
uc(0-)=U
37
38.
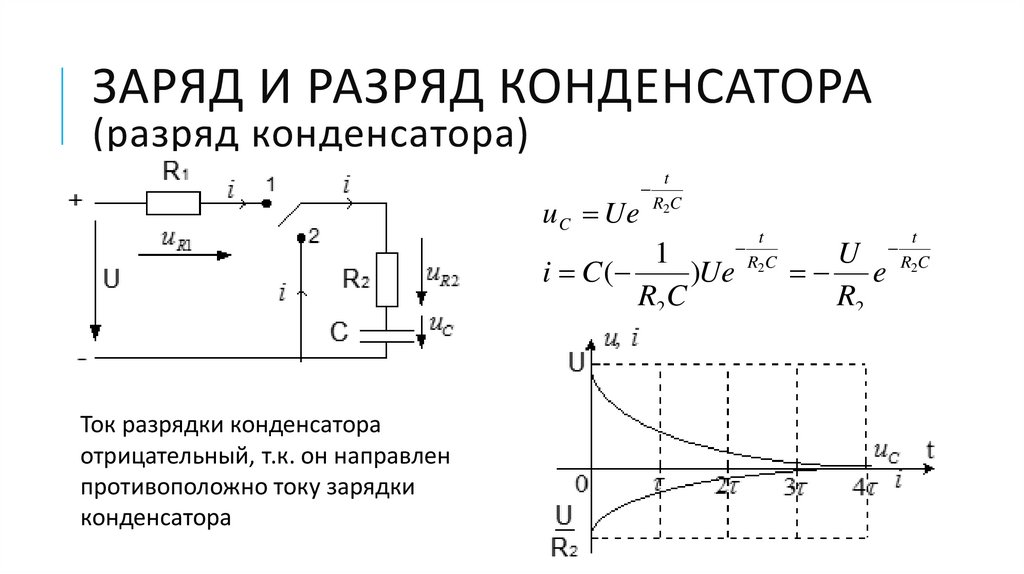
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(разряд конденсатора)
По II закону Кирхгофа для
послекоммутационной схемы
u R2 u C 0
Конденсатор заряжен до напряжения, равного приложенному
duC
i C
dt
uc(0-)=U
duC
R2 C
uC 0
dt
38
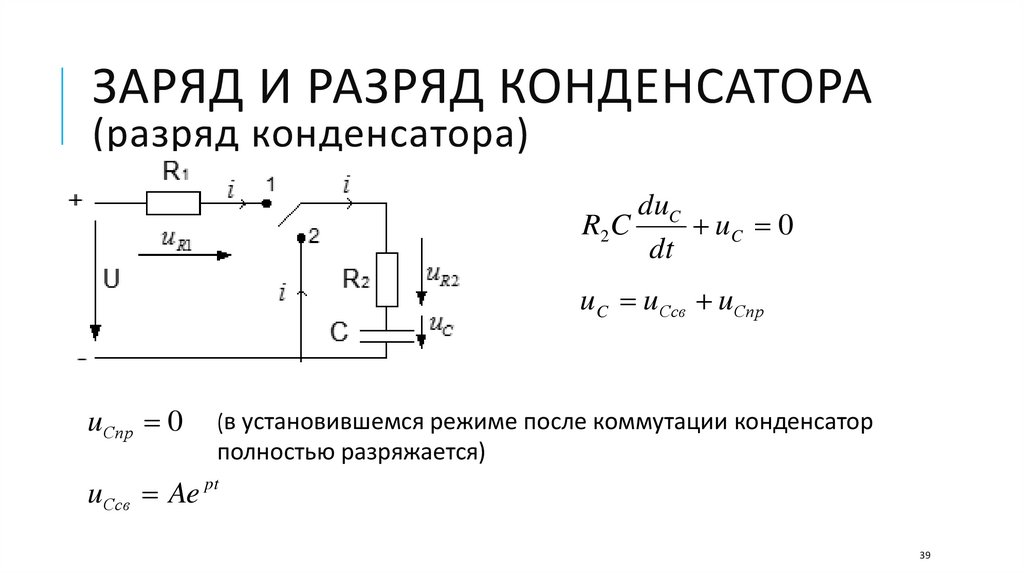
39.
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(разряд конденсатора)
duC
R2 C
uC 0
dt
uC uСсв uСпр
uСпр 0
(в установившемся режиме после коммутации конденсатор
полностью разряжается)
uСсв Ae pt
39
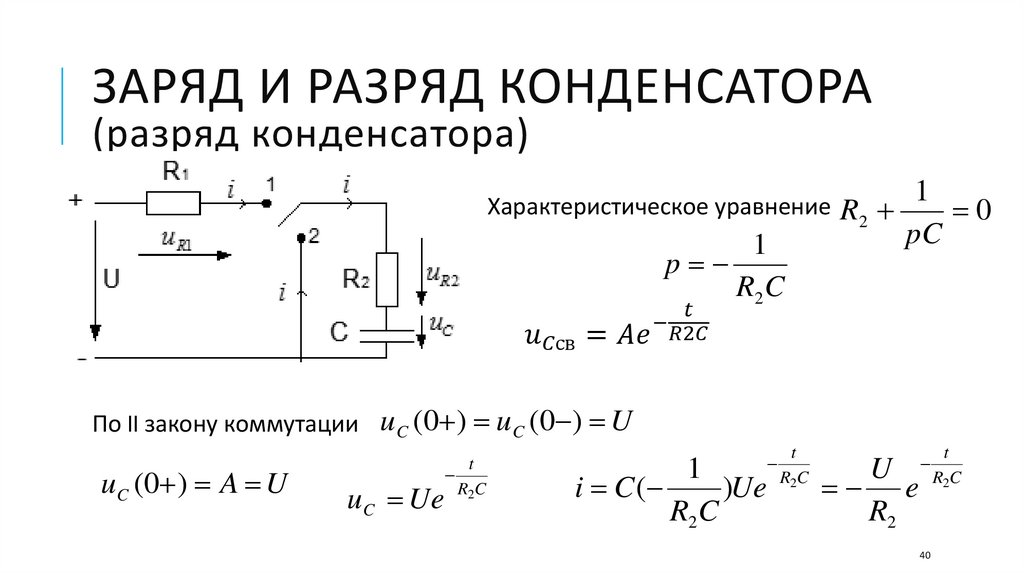
40.
ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА(разряд конденсатора)
Характеристическое уравнение R2
1
p
R2 C













 physics
physics electronics
electronics








