Similar presentations:
Переходные процессы в линейных цепях (лекция № 4.2)
1.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 4.2
по дисциплине
Электротехника
ТЕМА № 4
Переходные процессы в линейных
цепях
2.
Вопросы лекции4.2.1. Включение конденсатора на постоянное
напряжение (заряд конденсатора)
4.2.2. Разряд конденсатора
4.2.3. Включение конденсатора на переменное
напряжение
4.2.4. Переходные процессы в колебательном контуре
3.
4.2.1. Включение конденсатора на постоянное 37напряжение
(заряд конденсатора)
r
+
K
U
i(t)
-
Рис.1
Пусть конденсатор до включения
не был заряжен, т.е. u 0 0 .
c
После коммутации уравнение
C
второго закона Кирхгофа для контура
имеет вид: u r t u c t U
(1)
Учитывая, что u r t r i t , а
d uc уравнение (1) примет вид:
ic t c
dt
d uc
r c
uc t U
dt
или
d uc
uc t U
dt
(2)
Т.е. получили неоднородное дифференциальное уравнение первого порядка:
здесь r c - постоянная времени цепи.
Решение уравнения (2) состоит из двух составляющих:
(3)
uc t uc ус t ucсв t
где uc ус U - частное решение неоднородного уравнения, - установившееся
значение напряжения на емкости после окончания переходного процесса.
4.
K+
t
ucсв t A e τ - общее решение
U
36
r
однородного уравнения – свободная
составляющая напряжения на
C емкости; А – постоянная
интегрирования.
Характеристическое уравнение
1
и
его
корень
.
р
р 1 0
i(t)
-
Рис.1
Постоянную интегрирования А определим
из начальных условий:
1. Нулевые начальные условия при t 0, uc 0 0 .
Таким образом уравнение (3) принимает вид: u c 0 U A
(4)
следовательно, 0 U A , или A U .
t
t
u t U Ue τ U 1 e τ
Тогда,
c
Для тока в цепи имеем:
где
U
I
r
(5)
(6)
5.
+K
r
Напряжение на активном
сопротивлении равно:
t
u r t r i t U e
U
i(t)
-
Рис.1
35
(7)
C Из выражения (5) видно, что
напряжение на зажимах конденсатора
и заряд его нарастают по тому же
закону, что и ток в цепи r, L при
включении ее под постоянное
напряжение.
На рис.2 видно, что в начальный момент времени Ucсв(0+)=-U, а затем по
экспоненте стремится к 0. При t = 0– тока не было, при включении, т.е. при t =0+
U
ток сразу получает значение , т.к. момент t=0 напряжение на зажимах
r
конденсатора равно нулю, и ток в цепи определяется лишь напряжением U и
сопротивлением r. Напряжение Uc(t) складывается из графиков Ucуст и Ucсв
постепенно возрастает, и ток в цепи убывает по экспоненциальному закону. Все
сказанное относительно длительности переходных процессов в цепи с r, L
справедливо и для цепи r, С , так же и для любой цепи с одним накопителем
энергии.
6.
34uc
uc у =U
i
uc(t)
i
2τ
3τ
4τ
t
-U
Рис.2
2. Ненулевые начальные условия.
Если конденсатор до включения был уже заряжен, u c 0 0 , то постоянная
интегрирования А определится из условия: A u c 0 U
и выражения для u c t и i t
приобретают вид:
t
(8)
τ
uc t U uc 0 U e
U uc 0 τ
i t
e
r
t
(9)
7.
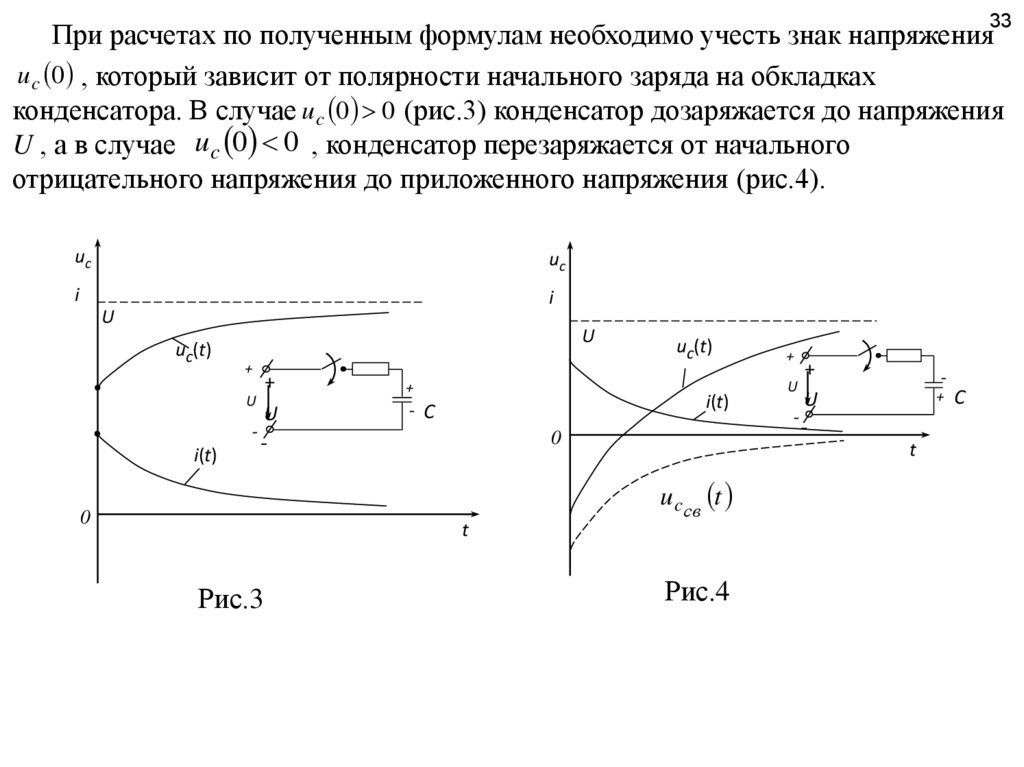
33При расчетах по полученным формулам необходимо учесть знак напряжения
u c 0 , который зависит от полярности начального заряда на обкладках
конденсатора. В случае u c 0 0 (рис.3) конденсатор дозаряжается до напряжения
U , а в случае uc 0 0 , конденсатор перезаряжается от начального
отрицательного напряжения до приложенного напряжения (рис.4).
uc
uc
i
i
U
uc(t)
i(t)
U
+
+
U
U
-
+
uc(t)
i(t)
- C
0
t
Рис.3
+
U
-
-
U
+ C
t
u c св t
0
+
Рис.4
8.
Если жеu c 0 U
32
, то на основании (8) и (9) имеем:
t
uc t U 1 2 e τ
t
2 U τ
i t
e
(10)
(11)
r
таким образом видим, что при некоторых значениях u c 0
свободная
составляющая при переходном процессе может резко возрастать, т.е. начальные
условия оказывают существенное влияние на переходный процесс в цепи.
Найдем, как распределяется энергия источника на создание электрического
поля и на тепловые потери в активном сопротивлении цепи, при нулевых
начальных условиях. Энергия источника равна:
t
Wu U I d t U I e d t C U 2
0
0
(12)
9.
Энергия, накопленная в электрическом поле конденсатора:2
2t
C
U
WЭ uc i d t U I e d t
2
0
0
WT
31
(13)
2
2t
C
U
2
2
ri dt r I e dt
(14)
2
таким образом из выражений (12-14) видно, что энергия, отданная источником
за время заряда конденсатора, распределяется поровну между электрическим
полем и тепловыми потерями в активном сопротивлении. Это соотношение
сохраняется независимо от величины сопротивления или емкости С.
Выражение для напряжений на емкости в начальный период переходного
процесса при t найдем, разложив функцию (5) в ряд и ограничившись
двумя первыми членами ряда, т.к.
0
0
t
2
3
t
1
t
1
t
t
e 1 1
2 !
3!
, то
t U
u c U 1 1 t
τ τ
т.е. напряжение на емкости в начале переходного процесса (при t )
изменяется во времени по линейному закону и определяется лишь напряжением
источника энергии и постоянной времени цепи.
10.
304.2.2. Разряд конденсатора
Предположим, что конденсатор был
заряжен от источника постоянного
i(t)
r
напряжения.
K
U
Uc + +
В цепи (рис.1), в установившемся
C
- режиме до замыкания ключа К ток не
протекает, и напряжение на конденсаторе
Рис.1
равно напряжению источника U.
Пусть в какой-то момент времени замыкается ключ К, электрическая связь
между контуром источника и контуром r, C теряется и в последнем начнется
переходный процесс, т.е. конденсатор будет разряжаться на сопротивление r.
По второму закону Кирхгофа для контура r - C имеем:
u r t uc t 0
(1)
d uC
где u r t r i t , а ic t C
, тогда, учитывая, что r c
, получим:
dt
+
r1
τ
d uC
uc t 0
dt
(2)
11.
+r1
i(t)
K
U
Рис.1
Uc
+
-
Поскольку уравнение (2) является
однородным, напряжение u c t при
r переходном процессе будет иметь только
+ свободную составляющую и после его
C
- окончания будет равно нулю:
t
(3)
τ
uc t uc е A e
св
из начальных условий найдем постоянную интегрирования А. При t=0,
u c 0 U . Причем, положительный знак u c 0 определяется правилом:
положительное направление u c 0 совпадает с направлением тока заряда I
от источника. Таким образом, A=U, тогда
t
(4)
u c е U e τ
Ток в цепи
t
t
d uC
U τ
i t C
e I e τ
dt
r
t
u r t r i t U e τ
(5)
(6)
29
12.
На рис.2 построены графики для u c t u i t (на основании формул (4),(5), характеризующие процесс разрядки конденсатора. Электрические процессы
при разряде конденсатора заключаются в том, что энергия электрического поля
за время переходного процесса преобразуется в тепло на активном
сопротивлении.
2
2 2t
C
U
U
r
2
Действительно,
uc
WT r i d t
e d t 2 WЭ
0
0
i
28
U
uc(t)
0
-I
i(t)
t
Постоянная времени r c в реальных
устройствах может иметь самые различные
значения. Например, если конденсатор с
емкостью С =100мкФ разряжается через
сопротивление r =100 Ом, то
6
100
10
100 0,01 C
Рис.2
Если тот же конденсатор оставить заряженным и отключенным от остальной
цепи, то он будет медленно разряжаться через свое сопротивление утечки.
8
Пусть это сопротивление составляет 10 Ом. Тогда
100 10 6 10 8 10 4 C 27,8 час, т.е. конденсатор с такой хорошей
изоляцией сохранит через сутки примерно одну треть своего начального заряда.
13.
4.2.3. Включение конденсатора на переменное 27напряжение
K
u U m sin t u
где u - начальная фаза напряжения
источника, соответствующая моменту
C
замыкания ключа. Напряжение на
обкладках конденсатора в
Рис.1
установившемся режиме равно:
U
(1)
uc уст t m sin t u
zωc
2
2
1
1
, arctg
z r 2
c
r c
i(t)
u
где
r
φ- угол сдвига фаз между установившимся током в цепи и приложенным
синусоидальным напряжением.
Свободное напряжение на емкости:
t
u t A e
(2)
где
r C .
c св
14.
26Следовательно для переходного процесса имеем:
t
(3)
Um
uc t
sin t u A e
z c
2
Постоянная А определяется из начального условия, согласно которому
должно быть задано напряжение на зажимах конденсатора до включения цепи.
Если конденсатор не был заряжен, то при t=0 напряжение u c 0 0 , и,
следовательно, u 0 U m sin A , откуда
c
u
z c
2
(4)
Um
A
sin u
z c
2
Окончательно напряжение на емкости равно:
t
uc t U mc sin t u U mc sin u e
2
2
где U m c
U
Um
I
m , здесь I m m
z
z c c
(5)
15.
25Для тока в переходном процессе в этом случае получим:
i t C
I
d uC
i у t iсв t m cos t u
dt
C
2
t
Im
sin u e
C r C
2
t
Im
I m cos t u
sin u e
2
2 r C
2
t
I
I m cos t u m 2 sin u e
r C
2
Из полученных выражений видно, что переходный процесс зависит от
величин u и φ.
Зависимости переходного напряжения на конденсаторе от времени при
различных значениях разностей ψ-φ показаны на рис. 2 Их анализ позволяет
сделать следующие выводы.
16.
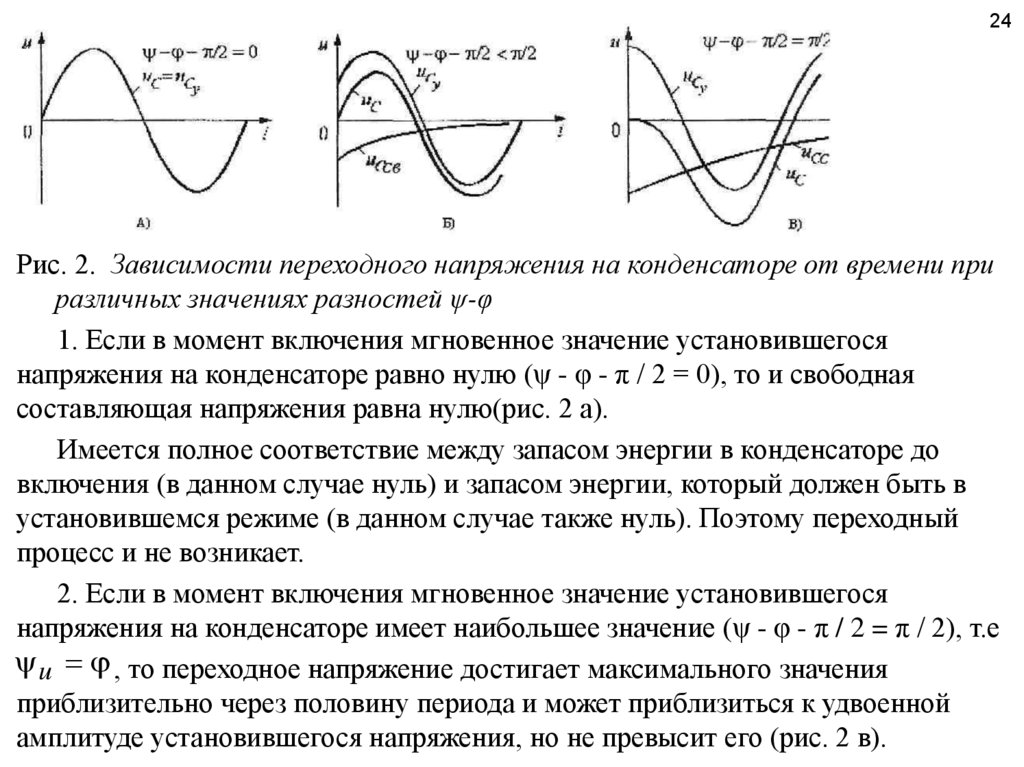
24Рис. 2. Зависимости переходного напряжения на конденсаторе от времени при
различных значениях разностей ψ-φ
1. Если в момент включения мгновенное значение установившегося
напряжения на конденсаторе равно нулю (ψ - φ - π / 2 = 0), то и свободная
составляющая напряжения равна нулю(рис. 2 а).
Имеется полное соответствие между запасом энергии в конденсаторе до
включения (в данном случае нуль) и запасом энергии, который должен быть в
установившемся режиме (в данном случае также нуль). Поэтому переходный
процесс и не возникает.
2. Если в момент включения мгновенное значение установившегося
напряжения на конденсаторе имеет наибольшее значение (ψ - φ - π / 2 = π / 2), т.е
u , то переходное напряжение достигает максимального значения
приблизительно через половину периода и может приблизиться к удвоенной
амплитуде установившегося напряжения, но не превысит его (рис. 2 в).
17.
Расчет переходных процессов классическим методомПоследовательность расчета переходных процессов классическим методом
можно, на основании рассмотренных примеров, производить следующим
образом:
1. С помощью законов Кирхгофа составляют уравнения для мгновенных
значений токов и напряжений для после коммутационных режимов.
2. Решаются полученные уравнения относительно одного неизвестного.
3. Записывается решение в виде суммы установившейся и свободной
составляющих.
4. Определяется установившаяся составляющая решения. Для ее определения
необходимо рассчитать установившийся режим цепи после коммутации
5. Используя правила коммутации и исходные уравнения, определяют
начальные условия.
6. Зная начальные условия, определяют постоянные интегрирования.
23
18.
7. Для определения других неизвестных токов и напряжений следуетиспользовать соотношения:
22
d uc
di
1t
1t
u L L ; uc i d t uc 0 ; il ul d t i 0 ; ic C
dt
C0
L0
dt
Порядок дифференциального уравнения определяется числом независимых
накопителей энергии. При одном накопителе переходный процесс описывается
дифференциальным уравнением первого порядка, при двух – второго и т.д.
Как уже известно, общее решение дифференциального уравнения
первого порядка имеет вид:
(1)
x t x уст t xсв t
где x уст t - частное решение неоднородного уравнения, характеризующее
новый установившийся режим в цепи;
xсв t - общее решение однородного уравнения, описывающее свободную
(затухающую) составляющую переходного процесса.
19.
При t=0 функция x t x 0 , а x уст t xсв 0 , тогдаA x 0 x уст 0
постоянная интегрирования
(2)
Следовательно, общая форма решения дифференциального уравнения
21
d x t
τ
x t y t
dt
описывающего переходный процесс в линейной цепи с одним накопителем,
имеет вид:
t
x t x уст t x 0 x уст 0 e
(3)
Постоянная времени определяется формулами:
L
или
rЭ С
rЭ
где rЭ - эквивалентное сопротивление цепи – сопротивление цепи по
отношению к зажимам накопителя энергии, при условии, что источники
энергии замкнуты накоротко, а их внутренние сопротивления сохранены в
соответствующих ветвях.
Применение общей формулы (3) существенно сокращает время,
затрачиваемое на расчет переходных процессов в цепях с одним накопителем.
Это сокращение особенно заметно в случае разветвленной цепи, когда для
получения общего дифференциального уравнения приходится использовать и
первый и второй закон Кирхгофа.
20.
4.2.4. Переходные процессы в колебательном 20контуре
Переходный процесс в этой схеме
обусловлен разрядом конденсатора на
+ +
U
C
- активное сопротивление и индуктивность.
L
Этот процесс протекает за счет энергии,
запасенной в электрическом поле.
Рис.1
По второму закону Кирхгофа имеем:
u r t u L t uc t 0
(1)
где
d uc
di
1
u r t r i t , u L t L
; u c i d t u c 0 ; i C
dt
C
dt
учетом приведенных соотношений можно получить два дифференциальных
уравнения для напряжения u c t и тока i (t).
d 2 uc r d uc
1
(2)
r
+
dt
и
2
d2 i
dt
2
L
dt
LC
u c t 0
r di
1
i t 0
L d t LC
(3)
21.
Для решения любого из этих дифференциальных уравнений (2) или (3)составим характеристическое уравнение: 2 r
1
р
L
р
LC
0
Найдем корни этого уравнения:
r
r2
1
р1, 2
2L
4 L2 L C
где r
2L
0
1
LC
р1, 2 2 02
или
- коэффициент затухания контура;
(4)
- угловая частота колебаний идеального контура,
т.е. контура без потерь r 0 , равная его резонансной частоте р .
Характер переходного процесса зависит от знака подкоренного выражения (4),
который и определяет, будут ли корни вещественными или комплексными.
19
22.
В зависимости от параметров схемы возможны три вида корнейхарактеристического уравнения, т.е. три вида переходного процесса:
1. Если
r2
1
4 L2 L C
2. Если
r2
1
- предельно- апериодический.
4 L2 L C
3. Если
r2
1
2
LC
4L
- апериодический.
- колебательный.
23.
Апериодический переходный процессПри подключении источника постоянного напряжения iуст(t) = 0, так как
постоянный ток через конденсатор не течет:
Ток в цепи представляет собой сумму двух экспонент (рис.2)
Рис.2
24.
При этом разряжается конденсатор, заряженный до напряжения U 0 черезрезистор и катушку индуктивности, и напряжение на конденсаторе монотонно
уменьшается от значения
до нуля, т.е. не происходит перезарядки
конденсатора.
С энергетической точки зрения это означает, что при разряде конденсатора
отдаваемая им энергия лишь в малой доле переходит в энергию магнитного
поля катушки, а большая часть ее поглощается в резисторе. Начиная с
некоторого момента времени, в тепло переходит не только оставшаяся энергия
электрического поля конденсатора, но и энергия, которая запаслась в
магнитном поле катушки.
закон изменения свободной составляющей представляет собой сумму двух
экспонент:
25.
Апериодический разряд конденсатора в цепи постоянного токаАпериодическим Апериодическое решение однородного
дифференциального уравнения, т.е. в нашем случае апериодический характер
свободного процесса (разряда конденсатора) имеет место, если корни
характеристического уравнения вещественны, т.е. если
U0
или
(5)
2
02 0
r 2
L
C
r2
1
4 L2 L C
18
26.
Графики зависимостей UR, UL, UC от времени приведены на рис. 2Рисунок. 2
27.
LC критическим сопротивлением контура.
Назовем
r - такое наименьшее его сопротивление, когда свободный процесс имеет еще
апериодический характер:
L
(6)
rкр 2
2
17
C
Корни р1 и р 2 вещественные и разные, если выполняется неравенство:
r rкр . Общее решение однородного дифференциального уравнения
второго порядка (2) при различных корнях представляется в виде:
P1 t
P2 t
(7)
uc t A1e
A2 e
где при условии (6) A1 , A2 - вещественные постоянные
интегрирования, определяемые из начальных условий, а р1 и р 2 - корни
характеристического уравнения. Заметим, что корни обязательно
отрицательны, т.к. свободный процесс должен быть затухающим во времени.
d uC
P t
P t
Ток
(8)
ic t C
C A1 P1 e 1 A2 P2 e 2
dt
из начальных условий u c 0 U 0 , i 0 0 при t = 0 определяем подставляя
начальные условия в выражения (7) и (8), получаем:
U 0 A1 A2 , 0 A1 P1 A2 P2
P2
P1
A1
U 0 , A2
U0
откуда
P2 P1
P2 P1
28.
U0P t
P t
u c t
P2 e 1 P2 e 2
P2 P1
i t
т.к.
Тогда
P1 P2 0
C U 0 P1 P2 P1 t
P t
e
e 2
P2 P1 L
1
LC
i t
и
pt
e 1
pt
U0
P t
P t
e1 e 2
P2 P1 L
p t
e 2
0
t
Рис.2
(10)
(11)
так как P2 0 , P1 0 и, кроме того, P2 P1 ,
то при изменении t от 0 до величины
убывают от 1 до 0 и при том разность
P t
P t
e 1 e 2 0 всегда положительна (рис.2).
Следовательно, ток i не меняет своего
направления, т.е. конденсатор все время
разряжается. В частности, при u c 0 U 0 0
ток все время отрицателен.
p t
e 1 e 2
(9)
Напряжение на индуктивности найдем по формуле:
U0
P t
P t
di
u L t L
P1 e 1 P2 e 2
d t P2 P1
16
29.
15На рис.3 изображены кривые i t , u r t r i t , uc t , u L t .
UU
В интервале времени 0 t t m ток по
i
абсолютному значению возрастает и достигает
uc(t)
P2 .
1
максимума при t t
l
m
n
P1 P2
P1
U0
u (t)
0
L
t m находится из условия
Значение
2 tm
imax
i t
d i uL
ur(t)
0 , т.е. из условия
-U0
i(t)
dt
L
P 1 tm
P 2 tm
P
e
P
e
0 .
1
2
z i(t)
В интервале времени t m t ток по
-U0
абсолютному значению убывает, стремясь к
Рис.3
нулю.
Напряжение на конденсаторе монотонно убывает, стремясь так же к нулю.
di
Из уравнения
u t L
r i
uLmax
tm
c
dt
следует, что напряжение на зажимах конденсатора в любой момент времени
уравновешивается суммой напряжения на зажимах катушки L и напряжения на
участке с сопротивлением r. В первый момент времени, когда r i 0 ,
напряжение на конденсаторе полностью уравновешивается напряжением на
зажимах катушки. Ток начинает возрастать по абсолютной своей величине
именно с такой скоростью, чтобы наступило такое равновесие.
30.
14В интервале времени 0 t t m
i
u c частично
(рис.3)
напряжение
uc(t)
уравновешивается напряжением на
U0
u (t)
катушке и частично напряжением на
u
max
tm
участке с сопротивлением.
2 tm
imax
t
i
ur(t)
С возрастанием t на долю катушки
-U0
i(t)
приходит все меньше напряжения и,
z i(t)
соответственно, скорость нарастания
-U0
Рис.3
тока уменьшается.
В момент времени t m величины u c и r i оказываются равными и
противоположными u c r i , т.е. оставшееся к этому моменту времени
напряжение uc полностью уравновешивается напряжением на
сопротивлении. Поэтому то дальше возрастать не может. В этот момент оно
достигает максимума, т.к. после этого момента оно должно убывать
вследствие того, что конденсатор продолжает разряжаться.
Напряжение на индуктивности u L изменяется от значения - U 0 , т.к. при
t 0 и ток, и напряжение на сопротивлении равны нулю, следовательно
uc u L .
U U0
L
L
31.
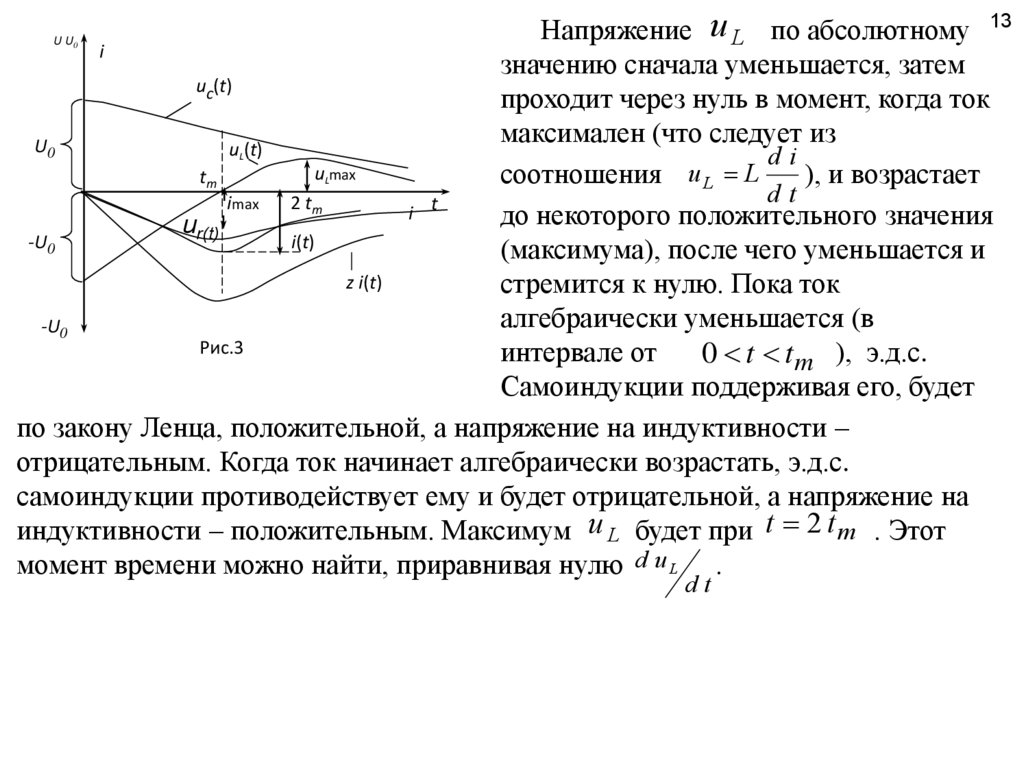
Напряжение u L по абсолютному 13i
значению сначала уменьшается, затем
uc(t)
проходит через нуль в момент, когда ток
максимален (что следует из
U0
u (t)
di
u max
соотношения u L L
), и возрастает
tm
d
t
2 tm
imax
i t
до некоторого положительного значения
ur(t)
-U0
i(t)
(максимума), после чего уменьшается и
z i(t)
стремится к нулю. Пока ток
алгебраически уменьшается (в
-U0
Рис.3
интервале от
0 t t m ), э.д.с.
Самоиндукции поддерживая его, будет
по закону Ленца, положительной, а напряжение на индуктивности –
отрицательным. Когда ток начинает алгебраически возрастать, э.д.с.
самоиндукции противодействует ему и будет отрицательной, а напряжение на
индуктивности – положительным. Максимум u L будет при t 2 t m . Этот
момент времени можно найти, приравнивая нулю d u L .
U U0
L
L
dt
32.
На рис.4, а показаны знаки напряжений u L и u r в интервале времени0 t t m, а также стрелкой с хвостовым оперением показано действительное
направление потока энергии в этот промежуток времени.
uL < 0
-
+
i<0
+
-
uc > 0
i<0
uc > 0
-
+
ur < 0
а
+
-
-
+
uL > 0
+
12
ur < 0
Рис.4
б
Напряжение u c и ток разных знаков и, следовательно мощность qc u c i
отрицательна, т.е. энергия отдается конденсатором из его электрического поля.
Напряжение u L и u r одного знака с током, и, следовательно, q L u L i 0
и P r i 2 0 , т.е. энергия поступает в катушку, запасаясь в ее магнитном
поле, и выделяется в виде тепла в сопротивлении.
u L 0 и uc 0 совместно
В интервале времени t m t
преодолевают сопротивление цепи, что легко видеть из рассмотрения знаков
напряжений, показанных на рис.4, б. Теперь мощность q L 0 , а катушка,
действительно так же, как и конденсатор, отдает запасенную энергию. Вся эта
энергия превращается в тепло.
33.
11Отметим влияние индуктивности на протекание процесса, для этого
сопоставим кривые рис.3 и рис.4. На рис. 3 кривые получены при L = 0. При
UU
таком условии в начальный момент
i
времени ток скачком принимает
uc(t)
значение, определяемое отношением
начального значения напряжения на
U0
u (t)
u max
конденсаторе к сопротивлению.
tm
2 tm
imax
При L 0 (рис.3) ток
i t
ur(t)
-U0
i(t)
увеличивается постепенно от
нулевого начального значения.
z i(t)
Следовательно, скорость спадания в
-U0
начальный период разряда при L 0
Рис.3
получается меньше, чем при L = 0.
0
L
L
uL < 0
-
+
uL > 0
+
i<0
-
+
-
+
uc > 0
-
+
-
+
ur < 0
а
i<0
ur < 0
Рис.4
б
uc > 0
34.
Предельно-апериодический разряд конденсатора в цепипостоянного тока
Предельный случай апериодического разряда конденсатора имеет
место, если сопротивление контура r rкр , т.е. корни характеристического
r
уравнения вещественные и равные: P1 P2 P
2L
L
2
2
Это имеет место при условии 0 , т.е. r rкр 2
.
C
При этом выражения для тока и напряжений становятся неопределенными
из-за равенства нулю и числителя и знаменателя.
Раскроем эти неопределенности по правилу Лопиталя, считая, что
P1 - переменная и стремится к P2 .
Для тока имеем:
P t
P t
U0 e 1 e 2
i t
L
p1 p2
U t e
t
U0
t
t e
L
(12)
Для напряжений
di
t
t
u
t
L
U
t
1
e
U
1
p
t
e
L
0
0
имеем:
dt
(13)
0
L
1t
t
uc t i d t U 0 t 1 e
U 0 1 p t e t
C0
(14)
10
35.
Можно найти максимальное значение тока i при t t m . Значение t mнаходим из условия (используя выражение 13):
t
U0
d i
m 0
0 , т.е t m 1 e
L
d t t tm
тогда
1 2L
1 t m 0 , t m
9
r
Следовательно, для тока имеем:
U 0 2 L 1
U0 2
U0
i t m
e
0,736
L
r
r e
r
Характер процессов в этом случае не отличается от рассмотренного выше
случая, когда 0 . Процесс также апериодический. Данный случай при
0 является предельным случаем апериодического разряда, так как при
дальнейшем уменьшении r ниже 2 L
разряд становится колебательным.
C
36.
Колебательный разряд конденсатора8
Разряд будет периодическим или колебательным, если сопротивление
контура будет меньше критического r rкр , т.е. корни характеристического
уравнения комплексные и сопряженные.
Это будет при условии, если 2 02 0, 02 2 . Обозначим
02 2 c (1), где c - угловая частота собственных или свободных
колебаний реального контура, т.е. контура, в котором учитываются потери
энергии в активном сопротивлении.
1
1
2
2
2
2
2
2
0
Тогда c 0 и 0 c
(2)
LC
LC
Корни характеристического уравнения можно записать в виде:
P1 2 02 j c 0 e
P2
2
j
j
02 j c 0 e
(3)
Решение дифференциального уравнения при комплексных корнях удобно
искать в виде
(4)
u A e t sin t
c
c
37.
Для определения постоянных интегрирования А и необходимоиспользовать второе уравнение:
ic t C
7
d uC
С A e t sin c t c cos c t
dt
так как начальные условия такие же как и в двух предыдущих случаях, то на
основании формул (4) и (5) имеем:
U 0 A sin ; 0 C A sin c cos
Откуда
c
c
c
tg
tg
; sin
c L C
2
2
2
1 tg
c 0
1
cos
L LC
2
2
2
1 tg
0
cos
L LC
1 tg 2
2 c2 0
1
U0
U0
0
A
U0
sin c L C c
38.
6Подставляя последние соотношения в выражения (4) и (5), получим:
0
uc t
U 0 e t sin c t
c
U 0 0 t
i t c
e
sin c t c cos c t
c
U 0 02 t
U 0 t
c
e
sin c t
e
sin c t
c
L c
(6)
(7)
U 0 0 t
U 0 t
di
u L t L
e
sin c t c cos c t
e
dt
c
c
U0
c
sin c t
cos c t
0 e t sin c t cos cos c t sin
0
0
c
(8)
U0
t
0 e
sin c t
c
39.
5Выражения (6), (7), (8) можно получить и по известным в предыдущих
случаях формулам
Для тока имеем:
i t
U0
U0
e t e j c t e t e j c t
e p1 t e p2 t
P1 P2 L
2 j c L
U0
e t sin c t I m e t sin c t
c L
U
где
Im 0
c L
Для uc t и u L t
имеем:
U0
U0
p2 t
p1 t
uc t
P2 e
P1 e
P1 P2
2 j c
(9)
(10)
0 e j e t e j c t 0 e j e t e j c t
U 0 0 t j c t
U 0 0 t
j c t
e
e
e
sin c t
e
2 j c
2 j c
40.
4U0
U0
p1 t
p2 t
u L t
P1 e
P2 e
P2 P1
2 j c
0 e j e t e j c t 0 e j e t e j c t
(11)
U 0 0 t j c t
j c t U 0 0
e
e
e t sin c t
e
c
c
На рис.1 изображены кривые u L , u.c ,
U
r i t u r t .
u
u r Кривая тока i подобна кривой
0
γ
c
γ
γ
0
2
2
c t
ur=r i
-U0
c t1
c t 2
T
c t3 c c
2
cTc
Рис.1
41.
Из полученных аналитических выражений, а так же из рисунка видно, чтопроцесс в этом случае является колебательным. Ток и напряжения на всех
участках периодически меняют знак. Амплитуда колебаний убывает по
показательному закону, следовательно, в цепи совершаются затухающие
колебания тока и напряжения. Угловая частота затухающих колебаний равна:
с
02 2
3
1
r2
L C 4 L2
Соответственно, период затухающих колебаний определяется по формуле:
2
2
Tc
(12)
c
1
r2
L C 4 L2
В предельном случае r 0 имеет:
0 , c 0 , Tc T0 2 L C
(13)
42.
В этом случае колебания будут незатухающими, так как энергия полей не 2рассеивается. Величину называют периодом незатухающих колебаний , а
формулу (13) называют формулой Томпсона. Угловая частота незатухающих
колебаний равна резонансной частоте контура. Учитывая, что при 0 угол
, получаем
2
U0
i
sin 0 t u L U 0 sin 0 t
u c U 0 sin 0 t
0 L
2
2
Кривые i , u L , u c для этого случая изображены на рис. 2.
uL,, i
i
2 t
2
uc
uL
Рис.2
Они полностью соответствуют характеру кривых при установившемся
процессе в случае резонанса.
При r 0 имеем: c 0 и Tc T0 .
43.
В предельном случае, когда r 2 L , т.е. , получаем c 0 и Tc .C
1
При этом колебательный разряд переходит в апериодический. Этот
предельный случай был рассмотрен ранее. Быстроту затухания принято
характеризовать так называемым декрементом колебаний , равным
отношению двух последующих амплитуд одного знака:
I e t : I e t Tc e Tc
(14)
Это постоянная величина, не зависящая от времени, а зависящая лишь от
параметров цепи r , L , C .
Часто быстроту затухания колебаний характеризуют натуральным
логарифмом этого отношения который называется логарифмическим
декрементом колебания .
(15)
ln Tc
При малом затухании Tc T0 (контура с высокой добротностью Q) имеем:
r 2
r
(16)
Tc
2
где - затухание контура.
2 L 0
2L
44.
Выражение (16) показывает, что для контуров с высокой добротностьюлогарифмический декремент затуханий мал. Следовательно, для этих контуров
можно разложить выражение для декремента колебаний и взять только два
первых члена:
(17)
1
Из (17) следует, что при высокой добротности контура его логарифмический
декремент колебаний показывает, насколько уменьшится максимальное
значение тока или напряжения за одно колебание. Если, например, контур имеет
добротность Q 100 , то на основании (16) находим:
0,0314
100
Отсюда 1 0,03 0,97 , т.е. за время одного колебания амплитуда
уменьшится на 3%.
45.
заключениеТаким образом, в результате рассмотрения материала вы получили знания :
о переходном процессе при включении конденсатора на постоянное
напряжение (заряд конденсатора);
о переходном процессе при разряде конденсатора;
о переходном процессе при включении конденсатора на переменное
напряжение;
о переходных процессах в колебательном контуре при включении RLC










































 physics
physics








