Анализ переходных процессов в разветвленных электрических цепях с одним реактивным сопротивлением

1. Тема 3. Переходные процессы в электрических цепях

2. Лекция 8. Анализ переходных процессов в разветвленных цепях с одним реактивным сопротивлением

3.

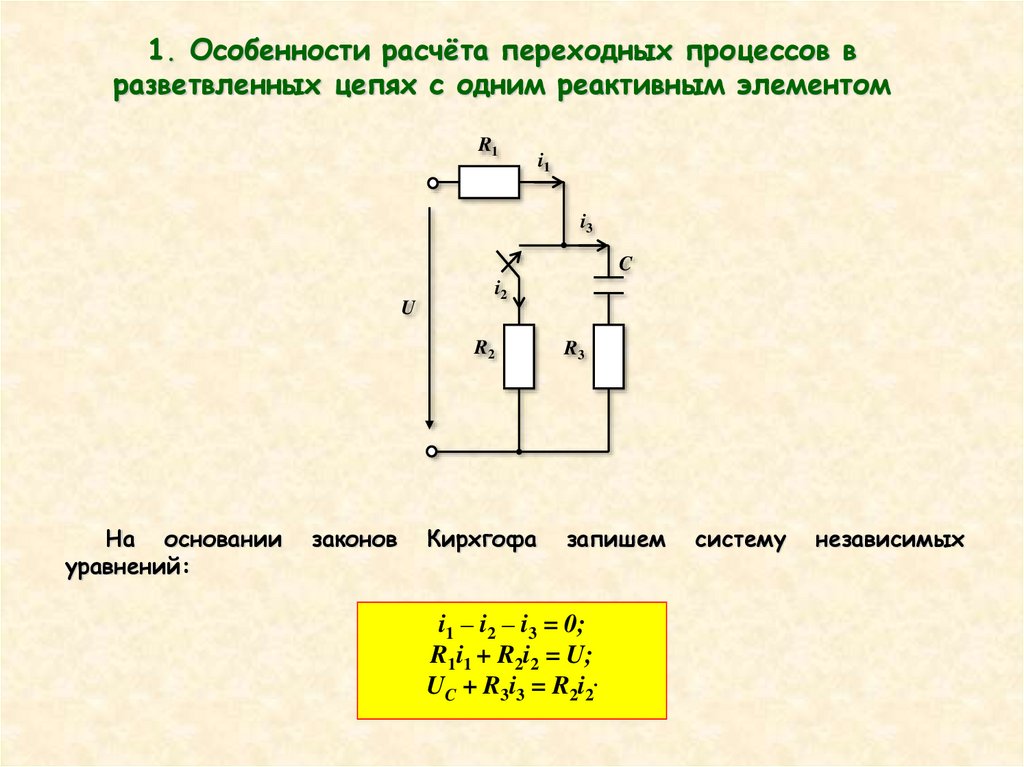
1. Особенности расчёта переходных процессов в
разветвленных цепях с одним реактивным элементом
R1
i1
i3
C
U
i2
R2
На основании
уравнений:
законов
Кирхгофа
R3
запишем
i1 – i2 – i3 = 0;
R1i1 + R2i2 = U;
UC + R3i3 = R2i2.
систему
независимых

4.

Так как
duc
i3 C
dt
, то из первого уравнения:
i1 i2 C
duc
dt
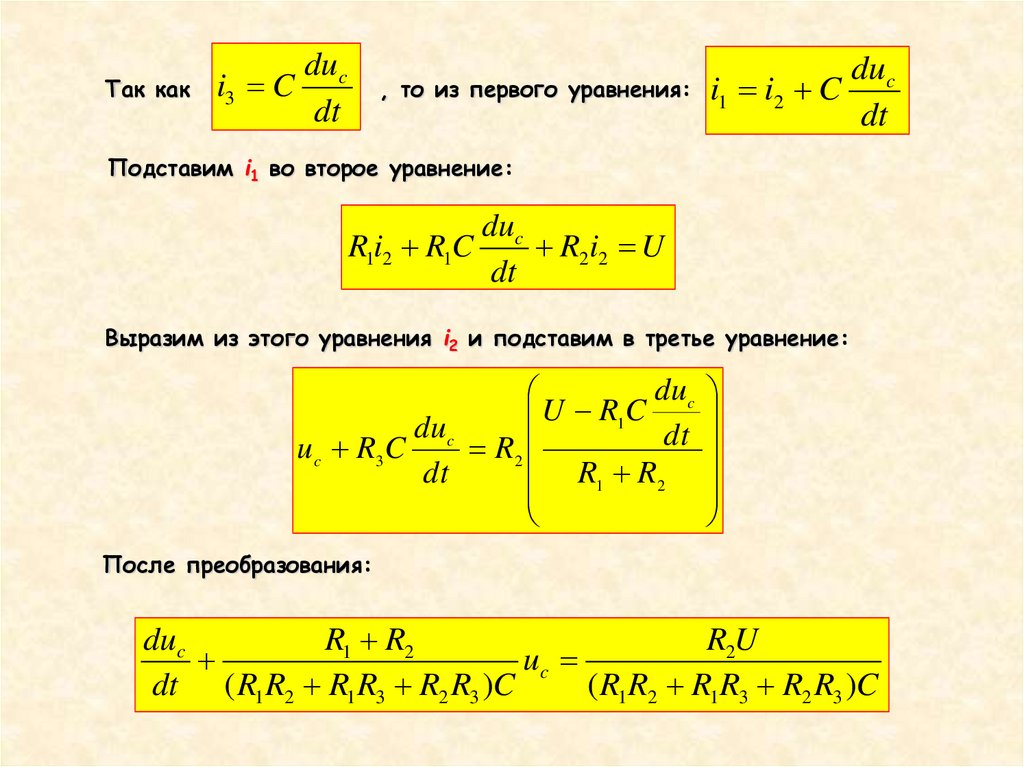
Подставим i1 во второе уравнение:
duc
R1i2 R1C
R2i2 U
dt
Выразим из этого уравнения i2 и подставим в третье уравнение:
duc
U
R
C
1
duc
dt
u c R3 C
R2
dt
R1 R2
После преобразования:
duc
R1 R2
R2U
uc
dt ( R1 R2 R1 R3 R2 R3 )C
( R1 R2 R1 R3 R2 R3 )C

5.

Общее
решение
этого
дифференциального
переходное напряжение на ёмкости:
уравнения
–
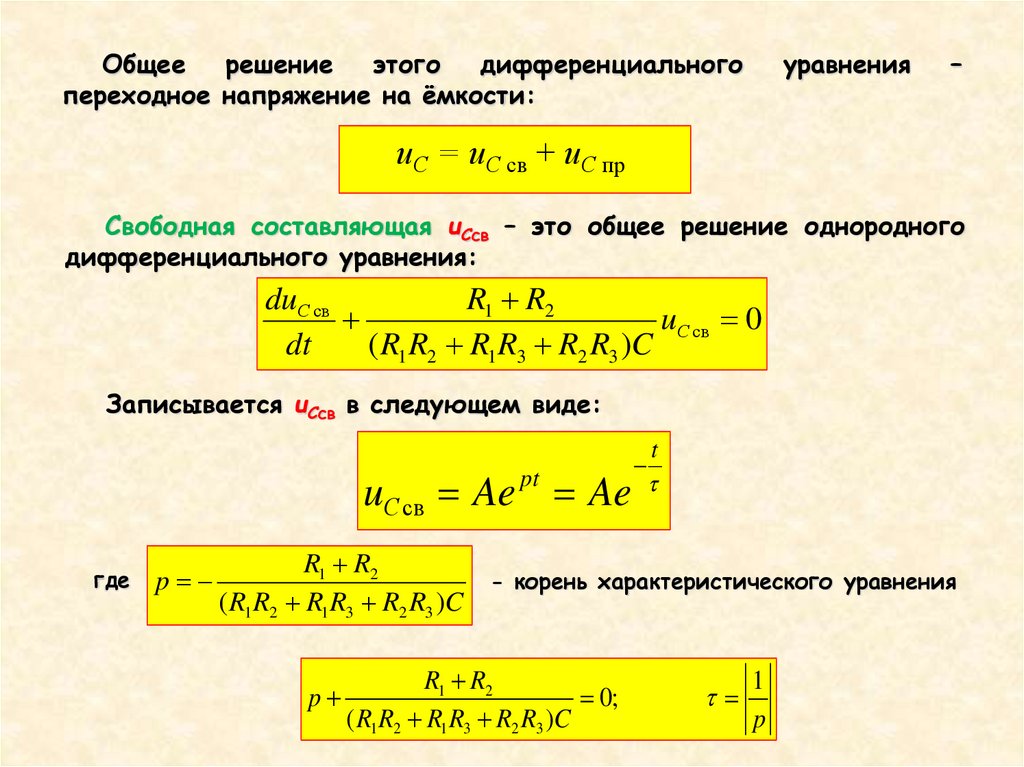
uC = uС св + uС пр
Свободная составляющая uСсв – это общее решение однородного
дифференциального уравнения:
duС св
R1 R2
uС св 0
dt
( R1 R2 R1 R3 R2 R3 )C
Записывается uСсв в следующем виде:
uС св Ae pt Ae
где
p
t
R1 R2
- корень характеристического уравнения
( R1 R2 R1 R3 R2 R3 )C
p
R1 R2
0;
( R1 R2 R1 R3 R2 R3 )C
1
p

6.

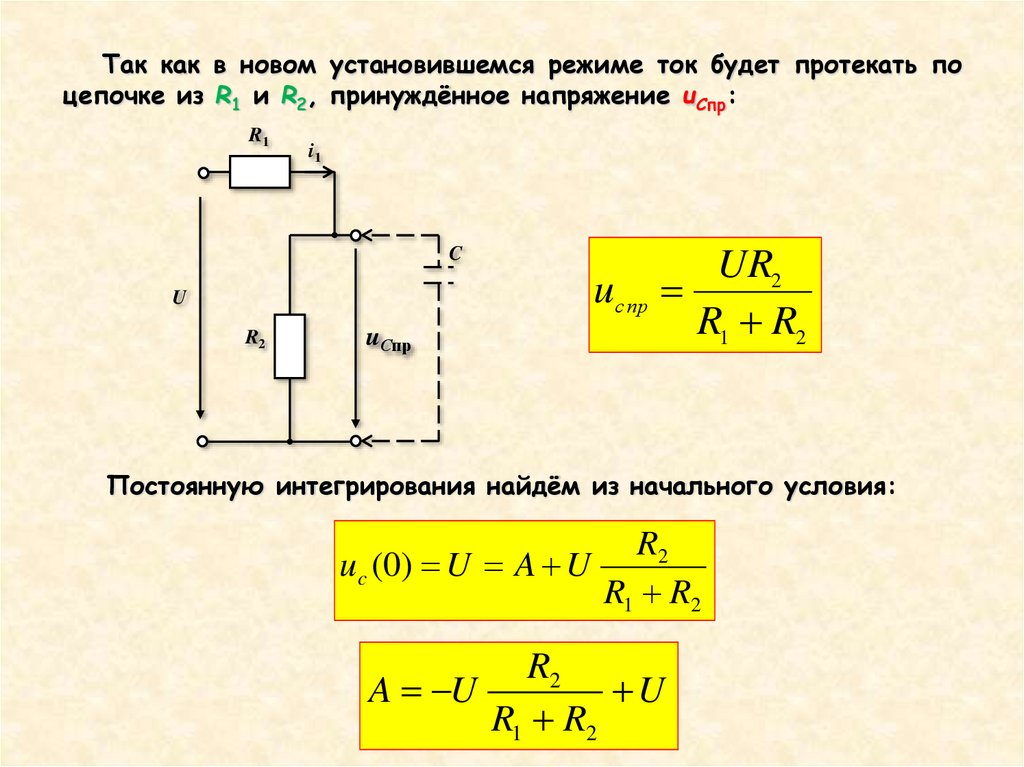
Так как в новом установившемся режиме ток будет протекать по
цепочке из R1 и R2, принуждённое напряжение uСпр:
R1
i1
C
uс пр
U
R2
uСпр
UR2
R1 R2
Постоянную интегрирования найдём из начального условия:
R2
uc (0) U A U
R1 R2
R2
A U
U
R1 R2

7.

Переходное напряжение на ёмкости:
uc (U U
R2
)e
R1 R2
t
U
R2
R1
U(
)e
R1 R2
R1 R2
Переходные токи получим из соотношений:
duc
uc R3i3
i3 C
; i2
; i1 i2 i3 .
dt
R2
t
U
R2
R1 R2

8.

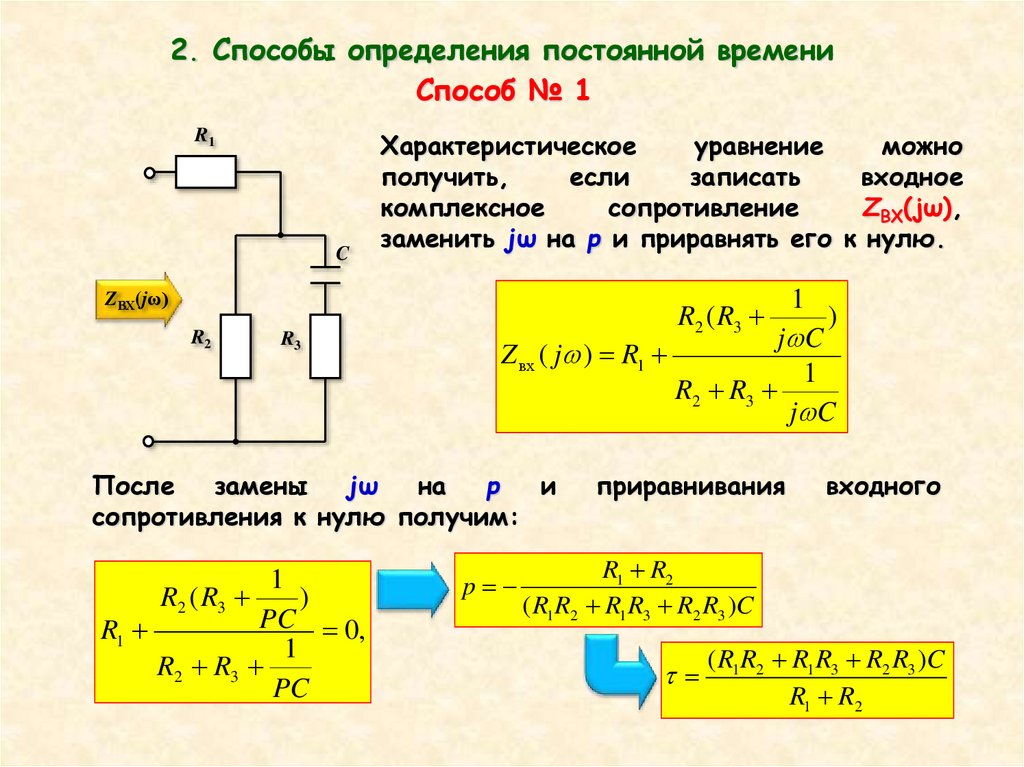
2. Способы определения постоянной времени
Способ № 1
R1
C
ZВХ(jω)
R2
R3
Характеристическое
уравнение
можно
получить,
если
записать
входное
комплексное
сопротивление
ZВХ(jω),
заменить jω на р и приравнять его к нулю.
1
)
j C
Z вх ( j ) R1
1
R2 R3
j C
R2 ( R3
После
замены
jω
на
р
и
сопротивления к нулю получим:
1
R2 ( R3
)
PC 0,
R1
1
R2 R3
PC
p
приравнивания
входного
R1 R2
( R1 R2 R1 R3 R2 R3 )C
( R1 R2 R1 R3 R2 R3 )C
R1 R2

9.

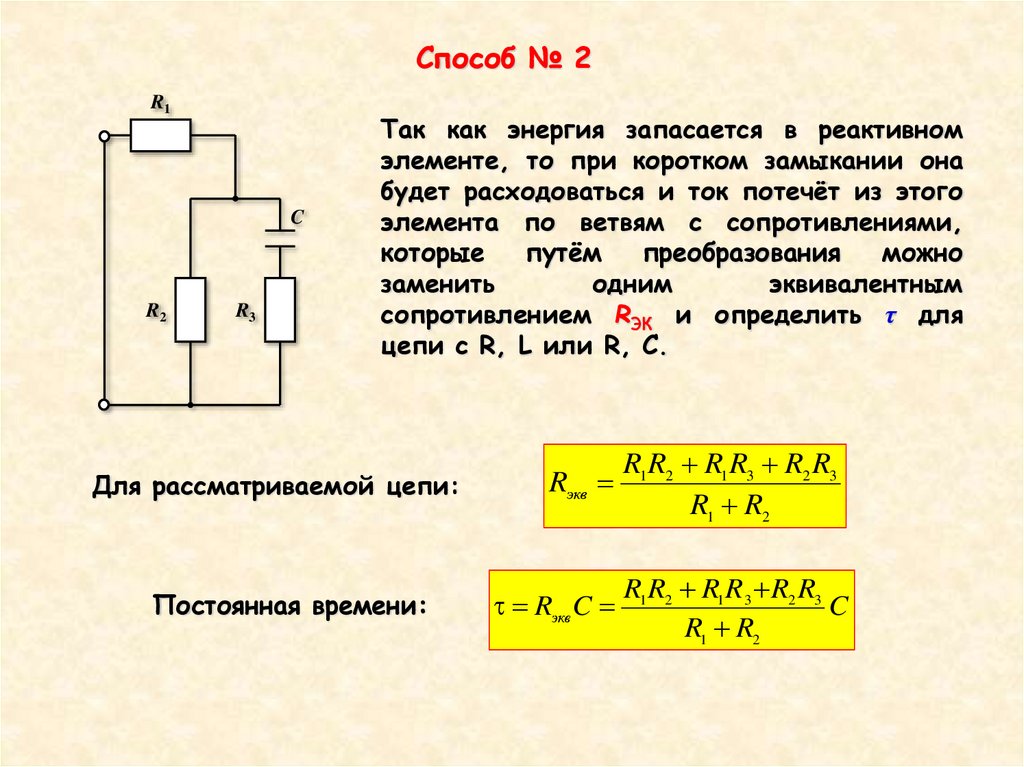
Способ № 2
R1
C
R2
R3
Так как энергия запасается в реактивном
элементе, то при коротком замыкании она
будет расходоваться и ток потечёт из этого
элемента по ветвям с сопротивлениями,
которые
путём
преобразования
можно
заменить
одним
эквивалентным
сопротивлением RЭК и определить τ для
цепи с R, L или R, C.
Для рассматриваемой цепи:
Постоянная времени:
Rэкв
R1 R2 R1 R3 R2 R3
R1 R2
R1 R2 R1 R 3 R2 R3
Rэкв C
C
R1 R2