Электротехника. Операторный метод анализа переходных процессов. (Лекция 13)

1.

Кубанский государственный технологический университет
Институт компьютерных систем и информационной и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника
Лекция № 13
Операторный метод анализа
переходных процессов

2.

Учебные вопросы:
1. Преобразования Лапласа и его свойства.
2. L –изображение элементов в электрических цепях.
3. Методика анализа переходных процессов в линейных
электрических цепях операторным методом.
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 185 –187.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории
электрических цепей и электроники: Учебник для вузов, - М.:
Радио и связь, 1999 г, с. 121 –132.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для
вузов, - М.: Высшая школа, 2003 г, с. 114 –122.

3.

1. Преобразования Лапласа и его свойства.
Операторный метод анализа позволяет сводить линейные
дифференциальные
уравнения
к
более
простым
алгебраическим уравнениям.
Формальные
правила
с
оператором
предложенные Хевисайдом (1892 г.)
дифференцирования,
2
n
d
d
d
p 0 1, p , p 2 2 ,..., p n n
dt
dt
dt
В основе операторного метода анализа переходных процессов лежит
преобразование Лапласа, которое позволяет перенести решение из
области функций действительного переменного t в область
комплексного переменного p:
p j
При этом методе нет необходимости определения постоянных интегрирования
c j
L( p ) f (t ) e pt dt
0
Прямое
Преобразование
Лапласа
1
pt
f (t )
L
(
p
)
e
dp
2 j c j
f (t ) M e , f (t ) 0при t 0
c0 t
Обратное

4.

c j
L( p ) f (t ) e pt dt
0
f (t ) L( p)
Изображение
по Лапласу
1
pt
f (t )
L
(
p
)
e
dp
2 j c j
L( p) L f (t )
Между парой преобразований Лапласа и
преобразований
Фурье
существует
связь:
преобразование Фурье есть частный случай
преобразования Лапласа при = 0.
Пример: Найдем
изображение по Лапласу f(t)=
от единичной функции
1, при t 0
0, при t 0
Оригинал
функции
p j
Используя
определение прямого
преобразования
Лапласа
1 pt
1 1
L( p ) f (t ) e dt 1(t ) e dt e / 0 0
p
p p
0
0
pt
pt
1
1(t )
p
Размерность L(p) = f(t) · t , т.е. размерность изображения равна
размерности оригинала, умноженной на время.

5.

Основные свойства (теоремы) преобразований Лапласа
1. Линейности
a1 f1 (t ) a2 f 2 (t ) ... a1 L1 ( p) a2 L2 ( p) ...
Это свойство позволяет находить изображение таких сигналов,
которые могут быть представлены суммами относительно простых
слагаемых с уже известными изображениями.
2. Дифференцирование оригинала
df (t )
d 2 f (t )
2
pL( p ),
p
L( p )
2
dt
dt
df (t )
pL( p ) f (0)
dt
Нулевые начальные условия
Ненулевые начальные условия
t
3. Интегрирование оригинала
0
4. Теорема запаздывания
5. Теорема смещения
t t
L( p )
L( p )
2
f (t )dt
; f (t )dt
0 0
p
p2
f (t t0 ) L( p ) e pt0
f (t ) е t L( p )

6.

6. Теорема свертывания (теорема умножения изображений)
t
t
0
0
L1 ( p ) L2 ( p ) f1 ( ) f 2 (t )d f1 (t ) f 2 ( )d
Таблица изображений по Лапласу
11
1
55
1
p
1
e
a
22
t
a
а
а
p
1
a p 1
p
77 (1 at ) exp( at )
( p a) 2
99
1
t 2
p
33
44
1
exp( at )
p a
a
66 1 exp( at ) p ( p a )
1 at 1 1
p
e 2 t 2
88
2
a
a a
p ( p a)
t 1 1 at
p
2 2e 2
a a a
p ( p a)
10
10
p
cos t 2
2
p

7.

sin t 2
p 2
11
11
13
13
14
14
15
15
16
16
12
12
exp( at ) sin t
( p a) 2 2
p a
exp( at ) cos t
( p a) 2 2
1
1
at
bt
(e e )
b a
( p a ) ( p b)
( p a) cos sin
exp( at ) cos( t )
( p a) 2 2
( p a) sin cos
exp( at ) sin( t )
( p a) 2 2
17
17
(t ) 1
Пользуясь основными свойствами преобразований
Лапласа, можно получить основные законы
электрических цепей в операторной форме.

8.

2. L - изображение элементов в электрических цепях
Емкостной элемент
Соотношение между L – изображением тока в емкостном элементе и
оригиналом i(t) определяется следующим соотношением (по теореме
дифференцирования):
duC (t )
i (t ) C
C pU C ( p) U C (0) I ( p)
dt
L – изображение тока
в емкости
L – изображение
напряжения на емкости
С
I(p)
UC(0)/p
1/pC
UС(p)
I ( p) CpU C ( p ) CU C (0)
I ( p ) U C (0)
U C ( p)
pC
p
UC(0)
–
определяет
начальные
условия
на
емкостном элементе
1
X
(
p
)
C
С 1/pС
p C

9.

Индуктивный элемент
Соотношение между L – изображением тока в индуктивном элементе и
оригиналом uL(t) определяются следующей зависимостью
u L (t ) U L ( p )
diL (t )
u L (t ) L
p L I ( p ) L I ( 0) U L ( p )
dt
iL (t ) I L ( p )
Следовательно, L – изображение напряжения на индуктивном элементе
определяются зависимостью
U L ( p ) p L I ( p ) L I ( 0)
L pL
I(0)
I(0)
I(p)
L
pL
UL(p)
L·I(0)
Начальное
напряжение
X L ( p) p L
Определяет начальные условия задачи
(начальный ток)

10.

Операторные сопротивления
При нулевых начальных условиях:
Операторное напряжение
на емкостном элементе
(0) == 00
IILL(0)
UCC(0)
(0) == 00
U
1
U С ( p)
I ( p) Z C ( p) I ( p)
pC
1
Z C ( p) YC ( p ) 1 pC
pC
Z C ( p)
Операторные сопротивление
и проводимость емкостного
элемента
Операторное напряжение
U
(
p
)
p
L
I
(
p
)
Z
(
p
)
I
(
p
)
L
L
на индуктивном элементе
1
1 Операторные сопротивление
pL Z L ( p) YL ( p )
и проводимость индуктивного
Z L ( p ) pL
элемента
Резистивный элемент
I(p)
R
UR(p)
U R ( p) R I ( p) Z R ( p) I ( p)
Z R ( p) R
YR ( p ) 1
R

11.

Законы Ома и Кирхгофа в операторной форме
e(t)
L
С
b
a i(t) R
а
uR(t)
uL(t)
b
uC(t)
Эквивалентная схема в
операторной форме
Va(p) I(p)
а
R
UR(p)
pL
UL(p)
L·I(0) 1/pC UC(0)/p Е(р)
b
UC(p)
Обобщенный
Va ( p) Vb ( p) E ( p) LI (0)
закон Ома в
I ( p)
1
операторной форме
1
Z ( p ) R pL
pC
R pL
Vb(p)
pC
Полное сопротивление цепи в
операторной форме
U C ( 0)
p

12.

Первый закон Кирхгофа в операторной
форме:
алгебраическая
сумма
операторных токов в узле равна нулю
m
I
k 1
k
( p) 0
U Ck (0) Второй закон Кирхгофа в
I k ( p) Z k ( p) Ek ( p) Lk I k (0)
операторной форме
p
k 1
k 1
m
n
Алгебраическая сумма операторных падений напряжений в контуре
равна алгебраической сумме операторных ЭДС и напряжений контура
Методика анализа переходных процессов в линейных
электрических цепях операторным методом
1. Из расчета цепи до коммутации найти токи в индуктивности IL(0) и
напряжения на емкости UC(0).
2. По виду топологии исследуемой цепи, получившейся после
коммутации, составить эквивалентную операторную схему.
3. Выбрать метод расчета и найти изображение искомых величин.
4. По изображению искомых величин (с помощью таблицы
преобразований Лапласа) найти оригинал, т.е. искомую функцию

13.

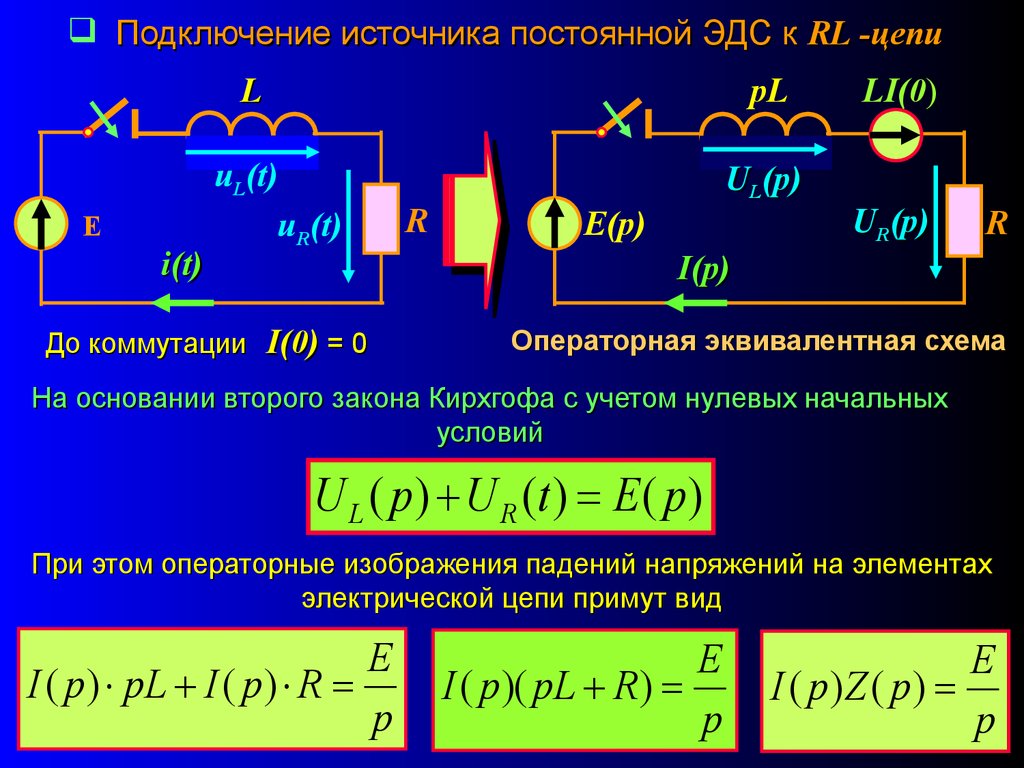
Подключение источника постоянной ЭДС к RL -цепи
L
Е
i(t)
pL
uL(t)
uR(t)
До коммутации
I(0) = 0
R
UL(р)
Е(p)
LI(0)
UR(р)
R
I(р)
Операторная эквивалентная схема
На основании второго закона Кирхгофа с учетом нулевых начальных
условий
U L ( p) U R (t ) E ( p)
При этом операторные изображения падений напряжений на элементах
электрической цепи примут вид
E
I ( p) pL I ( p ) R
p
E
I ( p )( pL R )
p
E
I ( p)Z ( p)
p

14.

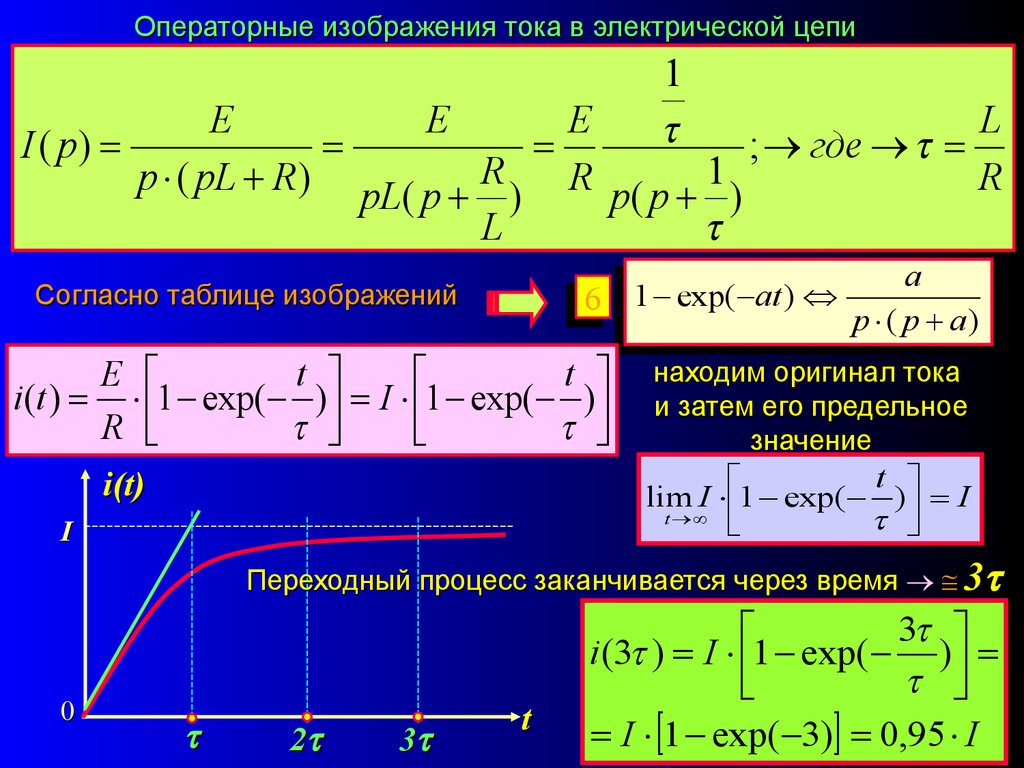
Операторные изображения тока в электрической цепи
1
E
E
E
L
I ( p)
; где
p ( pL R) pL( p R ) R p( p 1 )
R
L
Согласно таблице изображений
66
E
t
t
i (t ) 1 exp( ) I 1 exp( )
R
1 exp( at )
a
p ( p a)
находим оригинал тока
и затем его предельное
значение
t
lim I 1 exp( ) I
t
i(t)
I
Переходный процесс заканчивается через время 3
0
2
3
t
3
i (3 ) I 1 exp( )
I 1 exp( 3) 0,95 I

15.

Рассмотрим последовательный колебательный контур при ненулевых
начальных условиях, т.е. UC(0) 0 и IL(0) 0 .
L
Е
i(t)
uL(t)
uR(t)
С
Уравнение связи по второму закону
Кирхгофа имеет вид:
R
di (t ) 1
e(t ) i (t ) R L
dt
C
t
i(t )dt
t
uС(t)
di (t ) 1
i (t ) R L
i (t )dt U C (0)
dt
C0
Применив к этому выражению прямое преобразование Лапласа и
учитывая ряд свойств этого преобразования получаем:
1
U C (0)
E ( p) RI ( p) pL I ( p) LI (0)
I ( p)
pC
p
E ( p) LI (0) U C (0)
I ( p)
1
R pL
pC
Закон Ома в операторной
форме для данной цепи

16.

Включение колебательного контура на источник постоянного напряжения
Уравнение для изображение тока по закону Ома для нулевых
начальных условий примет вид:
I ( p)
E
p
E ( p)
E ( p)
C E
F1 ( p)
2
1
Z ( p) R pL 1
LCp
RCp 1 F2 ( p )
R pL
pC
pC
Определим корни
характеристического уравнения
F2 ( p ) LCp 2 RCp 1
R > 2
R
R 2 1
p1, 2 ( )
2L
2L
LC
Воспользовавшись теоремой разложения, которая позволяет при
нахождении оригинала операцию интегрирования заменить операцией
суммирования, что значительно упрощает расчеты
n
pk – корни характеристического уравнения
dF2 ( p )
F ( pk )
/ p pk
dp
2
F1 ( pk ) pk t
f (t ) *
e ,
k 1 F2 ( pk )
F2 ( p1 ) 2 LCp1 RC
F2 ( p2 ) 2 LCp2 RC

17.

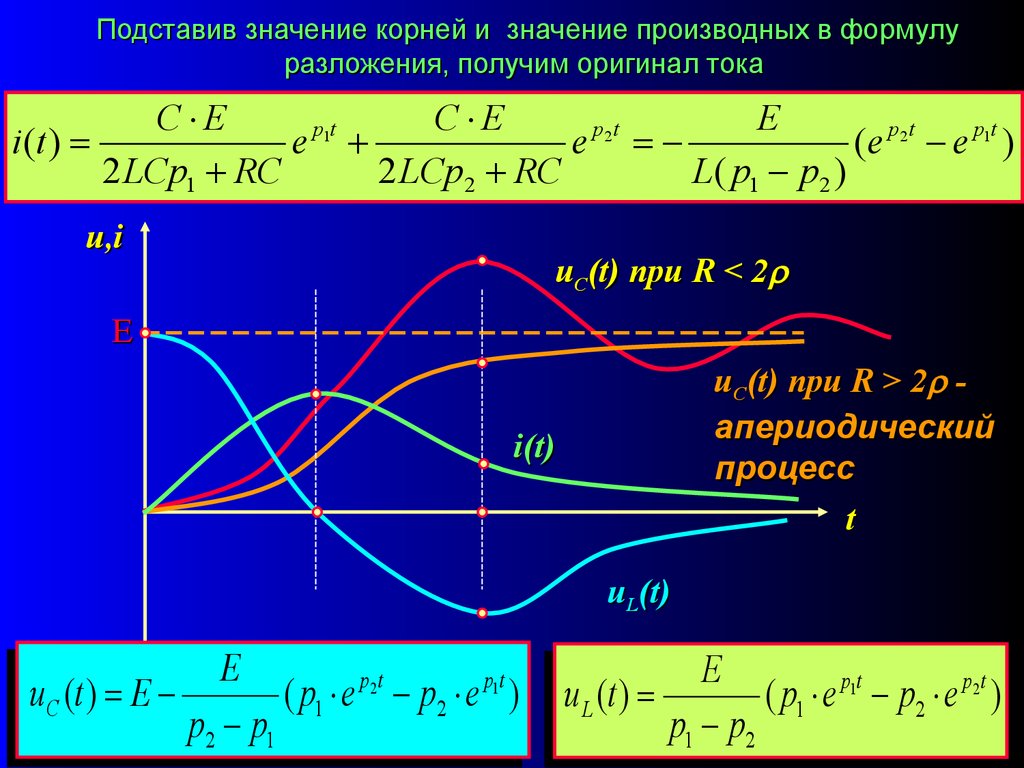
Подставив значение корней и значение производных в формулу
разложения, получим оригинал тока
C E
C E
E
p1t
p2t
i (t )
e
e
(e p2t e p1t )
2 LCp1 RC
2 LCp2 RC
L( p1 p2 )
u,i
uC(t) при R < 2
E
uC(t) при R > 2 апериодический
процесс
t
i(t)
uL(t)
E
p2t
p1t
uC (t ) E
( p1 e p2 e )
p2 p1
E
u L (t )
( p1 e p1t p2 e p2t )
p1 p2

18.

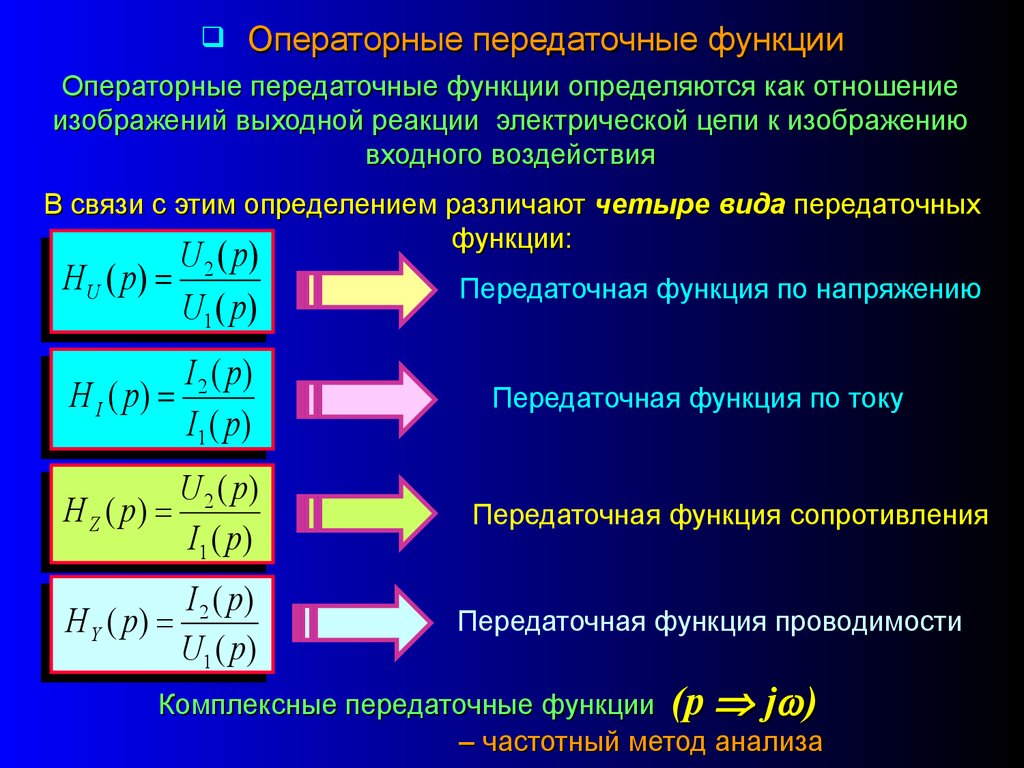
Операторные передаточные функции
Операторные передаточные функции определяются как отношение
изображений выходной реакции электрической цепи к изображению
входного воздействия
В связи с этим определением различают четыре вида передаточных
функции:
U 2 ( p)
HU ( p)
U1 ( p)
I 2 ( p)
H I ( p)
I1 ( p )
U 2 ( p)
H Z ( p)
I1 ( p )
I 2 ( p)
H Y ( p)
U1 ( p )
Передаточная функция по напряжению
Передаточная функция по току
Передаточная функция сопротивления
Передаточная функция проводимости
Комплексные передаточные функции (p j )
– частотный метод анализа

19.

Задание на самостоятельную работу
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 185 –187.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 121 –
132.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 114 –122.