Similar presentations:
Площадь треугольника. Вывод формулы
1. Площадь треугольника
Вывод формулы2. Задача №1
ВA
4
D
6
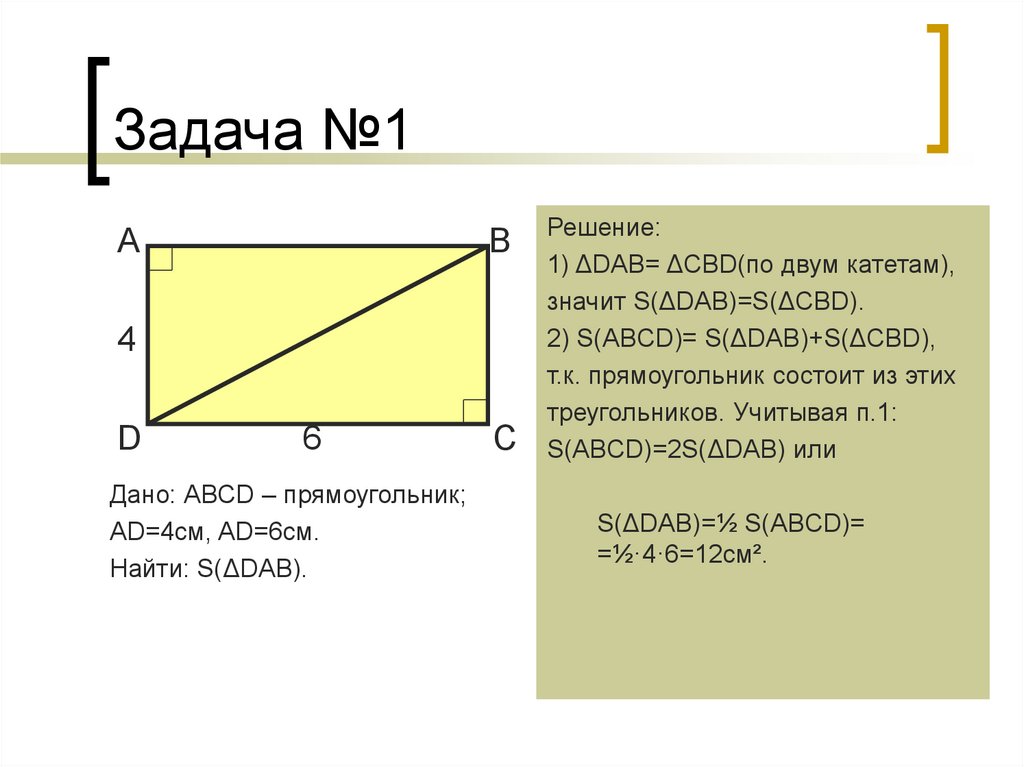
Дано: АВСD – прямоугольник;
АD=4см, AD=6см.
Найти: S(ΔDАB).
C
Решение:
1) ΔDАВ= ΔСВD(по двум катетам),
1)
значит
S(ΔDАВ)=S(ΔСВD).
2) S(ABCD)= S(ΔDАВ)+S(ΔСВD),
т.к. прямоугольник состоит из этих
треугольников. Учитывая п.1:
S(ABCD)=2S(ΔDАВ) или
S(ΔDАВ)=½ S(ABCD)=
=½·4·6=12см².
3. Гипотеза
Аa
В
D
C
b
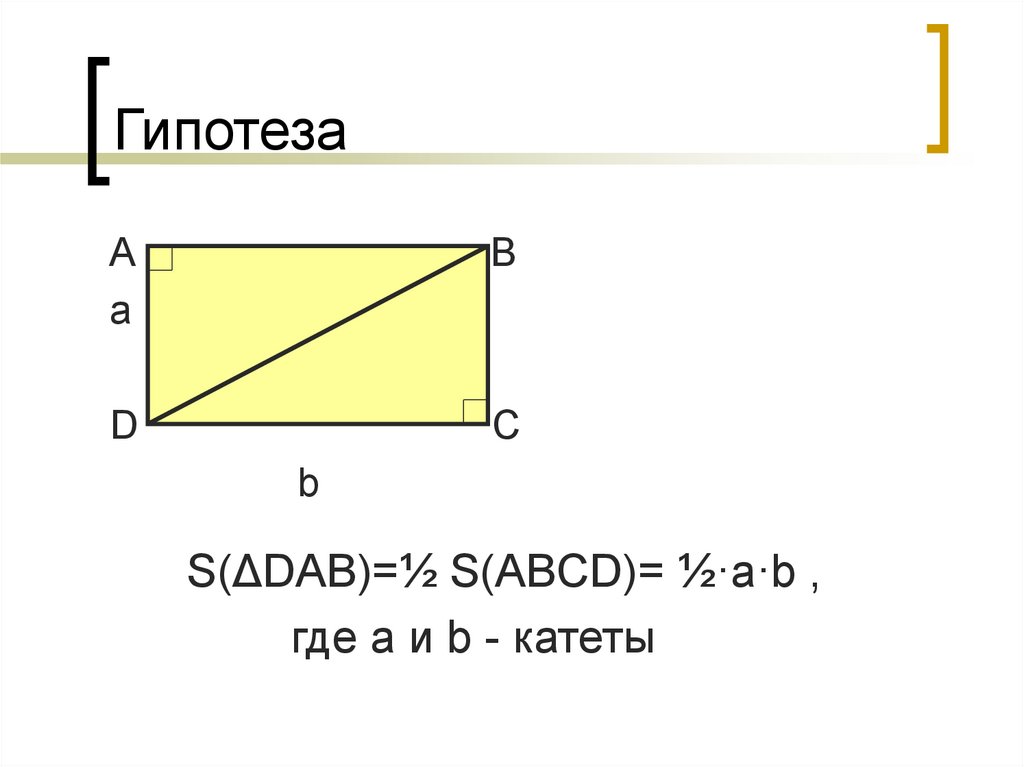
S(ΔDАВ)=½ S(ABCD)= ½·a·b ,
где а и b - катеты
4. Теорема №1
АЕ
С
В
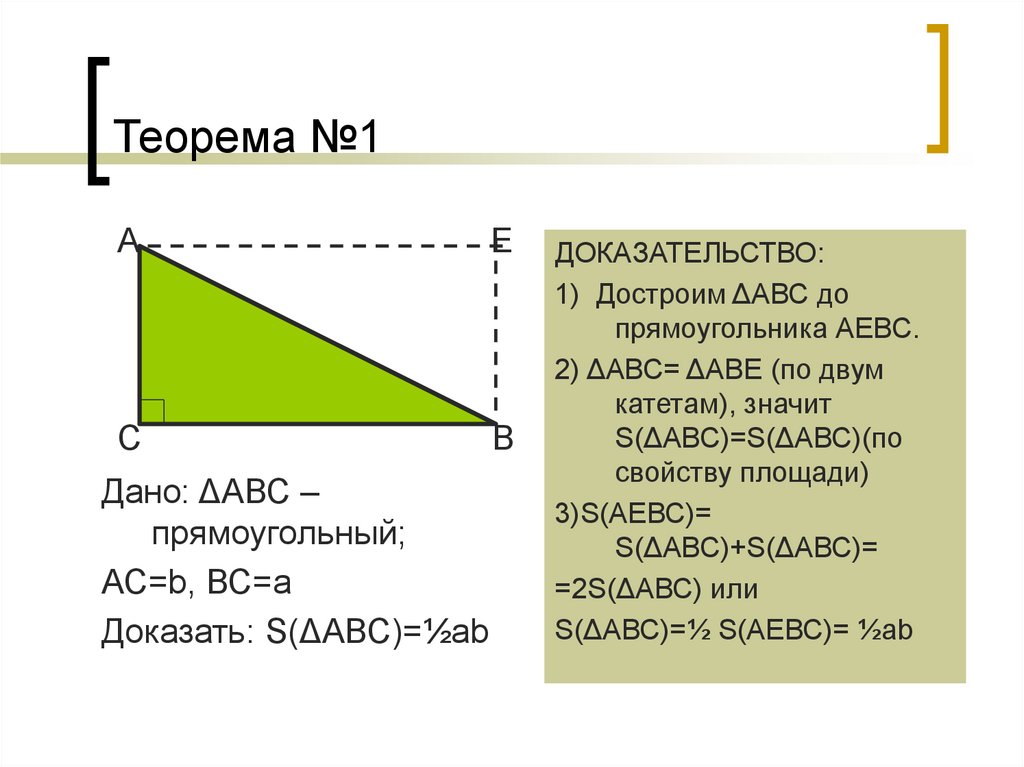
Дано: ΔАВС –
прямоугольный;
АС=b, ВС=а
Доказать: S(ΔАВС)=½ab
ДОКАЗАТЕЛЬСТВО:
1) Достроим ΔАВС до
прямоугольника АЕВС.
2) ΔАВС= ΔАВЕ (по двум
катетам), значит
S(ΔАВС)=S(ΔАВС)(по
свойству площади)
3)S(АЕВС)=
S(ΔАВС)+S(ΔАВС)=
=2S(ΔАВС) или
S(ΔАВС)=½ S(АЕВС)= ½ab
5. Задача №2
ВРешение:
1) S(ΔАВС)= S(ΔАВН)+S(ΔВНС)
по свойству площади, т.к. ΔАВС
состоит из ΔАВН и ΔВНС.
А 4
Н
6
С
Дано: ΔАВС; ВН – высота;
ВН=3см, АН=4см, НС=6см.
Найти:S(ΔАВС)
2) S(ΔАВС)= ½·4·3+ ½·6·3 =
=15см²
Замечание: если записать
решение в общем виде,
получим
S(ΔАВС)= ½·АН·ВН+
½·НС·ВН=
½·ВН(АН+НС)= ½·АС·ВН
6. Задача №3
А3
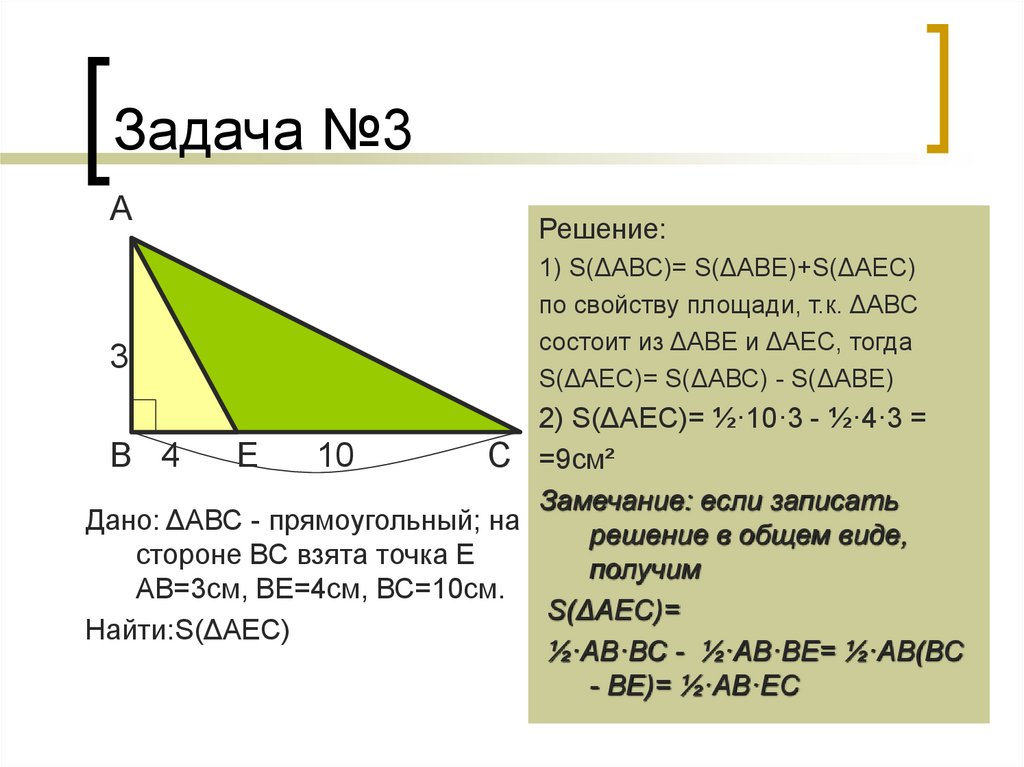
Решение:
1) S(ΔАВС)= S(ΔАВЕ)+S(ΔАЕС)
по свойству площади, т.к. ΔАВС
состоит из ΔАВЕ и ΔАЕС, тогда
S(ΔАЕС)= S(ΔАВС) - S(ΔАВЕ)
2) S(ΔАЕС)= ½·10·3 - ½·4·3 =
В 4
Е
10
С =9см²
Замечание: если записать
Дано: ΔАВС - прямоугольный; на
решение в общем виде,
стороне ВС взята точка Е
получим
АВ=3см, ВЕ=4см, ВС=10см.
S(ΔАЕС)=
Найти:S(ΔАЕС)
½·АВ·ВС - ½·АВ·ВЕ= ½·АВ(ВС
- ВЕ)= ½·АВ·ЕС
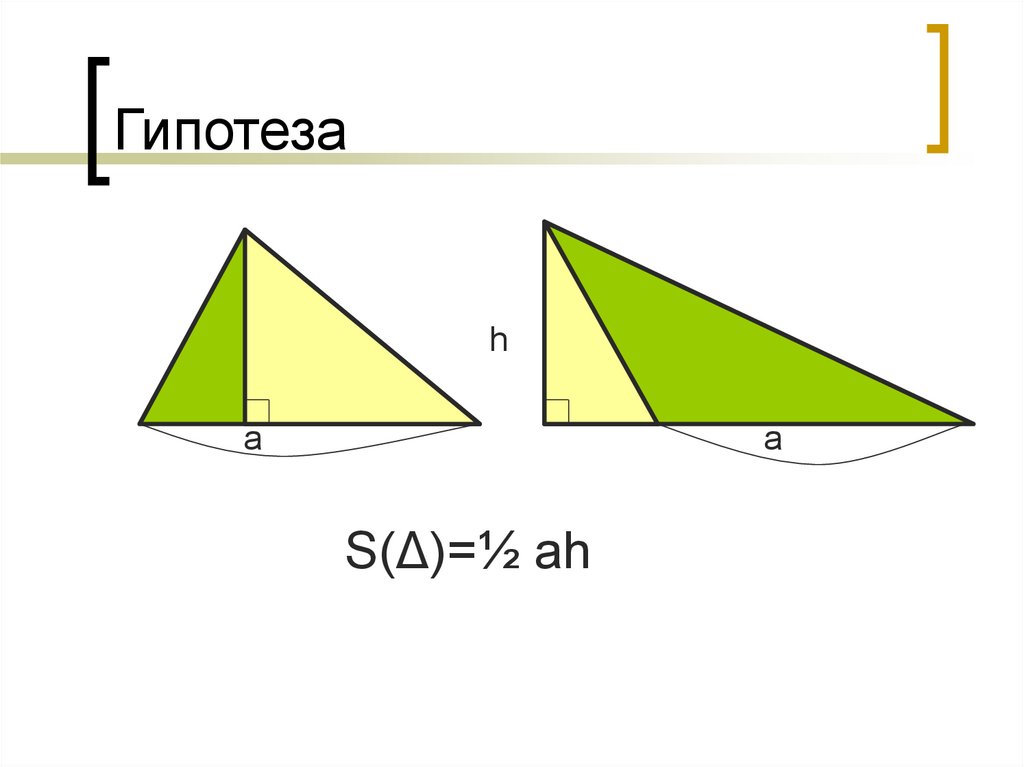
7. Гипотеза
hа
а
S(Δ)=½ ah
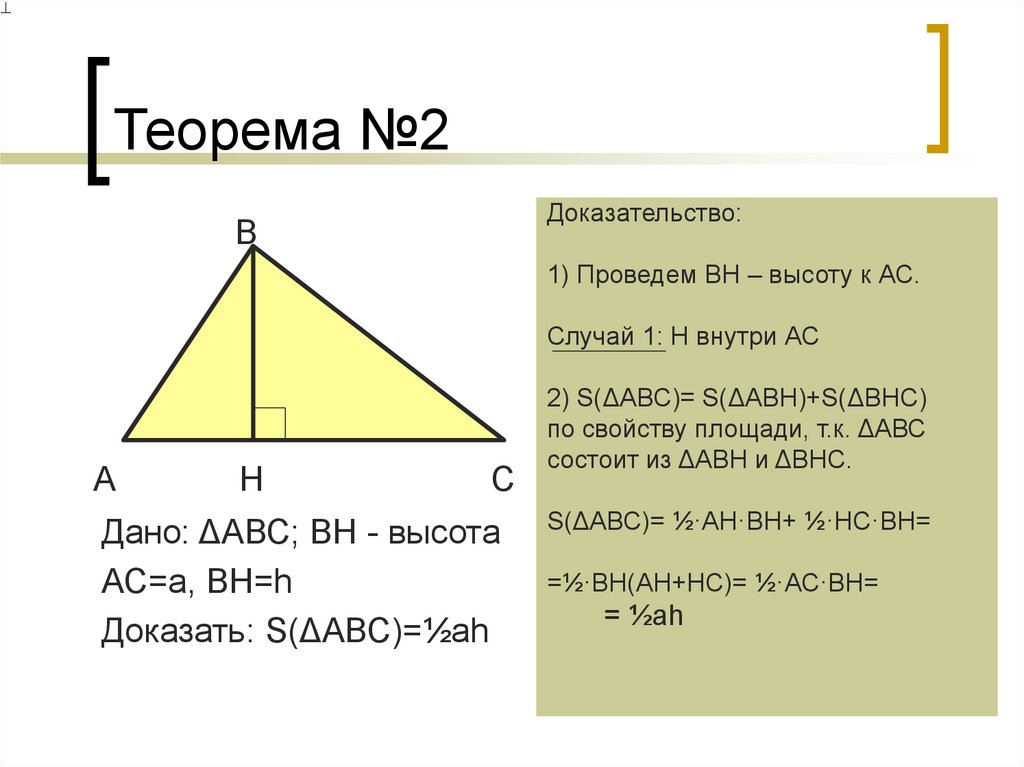
8. Теорема №2
Доказательство:В
1) Проведем ВН – высоту к АС.
Случай 1: Н внутри АС
А
Н
С
Дано: ΔАВС; ВН - высота
АС=a, ВH=h
Доказать: S(ΔАВС)=½ah
2) S(ΔАВС)= S(ΔАВН)+S(ΔВНС)
по свойству площади, т.к. ΔАВС
состоит из ΔАВН и ΔВНС.
S(ΔАВС)= ½·АН·ВН+ ½·НС·ВН=
=½·ВН(АН+НС)= ½·АС·ВН=
= ½ah
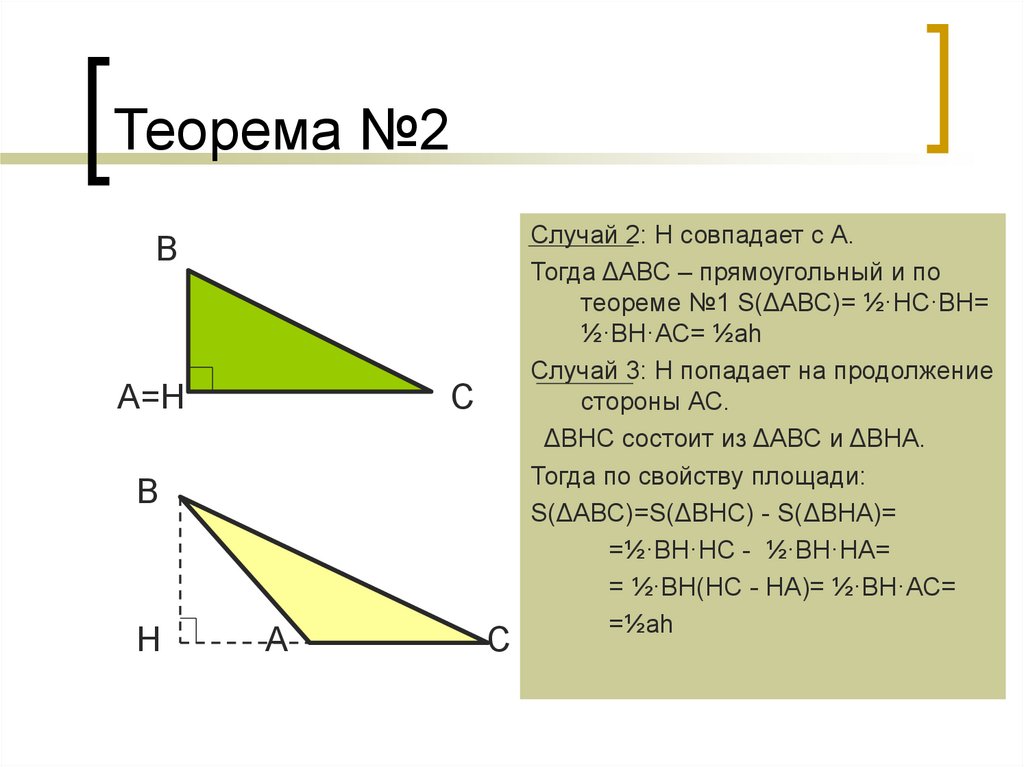
9. Теорема №2
ВА=Н
С
В
Н
А
С
Случай 2: Н совпадает с А.
Тогда ΔАВС – прямоугольный и по
теореме №1 S(ΔАВС)= ½·НС·ВН=
½·ВН·АС= ½ah
Случай 3: Н попадает на продолжение
стороны АС.
ΔВНС состоит из ΔАВС и ΔВНА.
Тогда по свойству площади:
S(ΔАВС)=S(ΔВНС) - S(ΔВНА)=
=½·ВН·НС - ½·ВН·НА=
= ½·ВН(НС - НА)= ½·ВН·АС=
=½ah


 mathematics
mathematics








