Similar presentations:
Площадь треугольника и трапеции
1.
8 класс2. Устная работа.
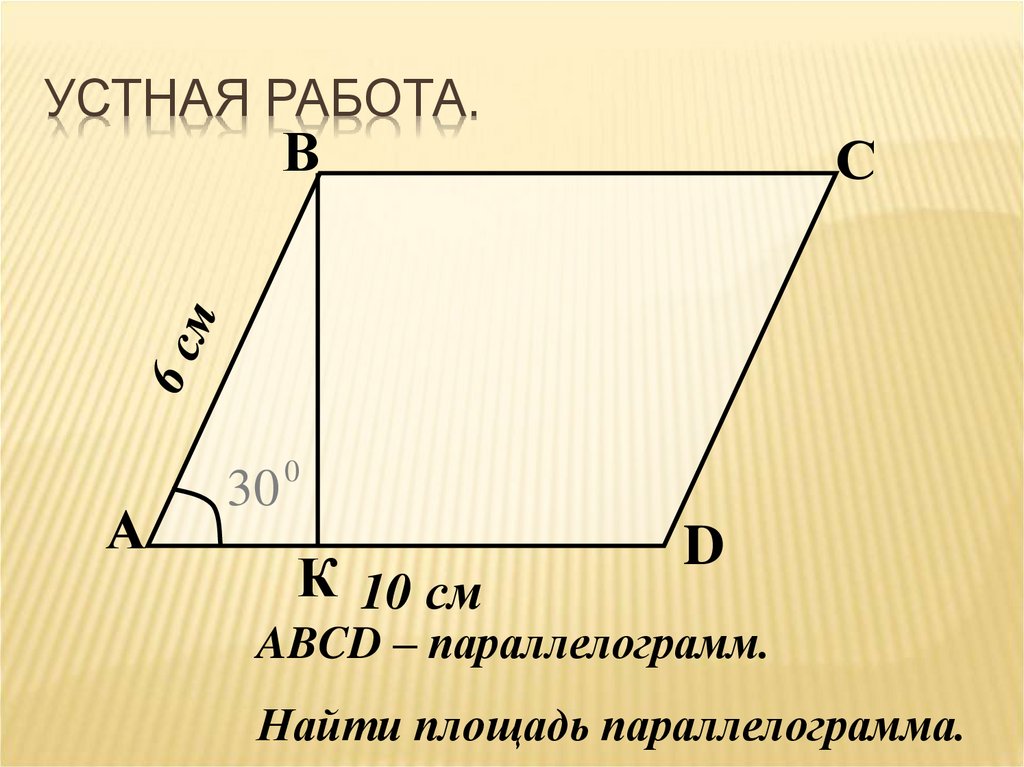
УСТНАЯ РАБОТА.В
А
30
С
0
К 10 см
D
ABCD – параллелограмм.
Найти площадь параллелограмма.
3. Устная работа.
УСТНАЯ РАБОТА.В
60
А
С
0
8 см
D
ABCD – параллелограмм.
Найти площадь параллелограмма.
4.
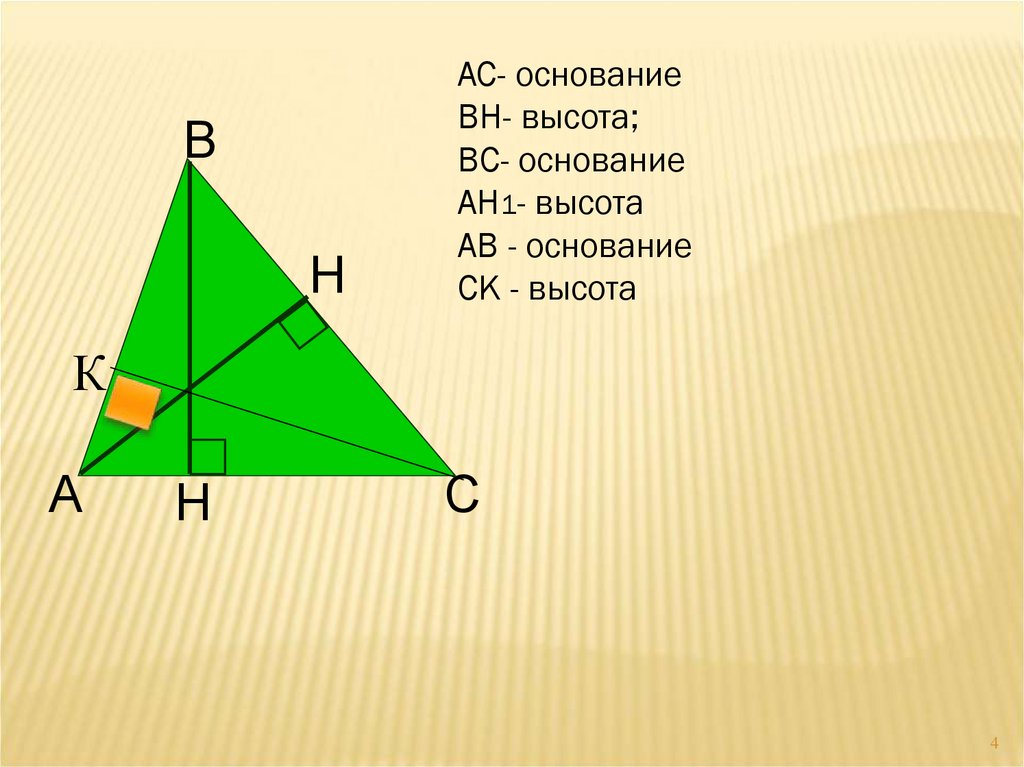
ВН1
АС- основание
ВН- высота;
ВС- основание
АН1- высота
АВ - основание
СК - высота
К
А
Н
С
4
5. Теорема. Площадь треугольника равна половине произведения его основания на высоту.
ТЕОРЕМА. ПЛОЩАДЬ ТРЕУГОЛЬНИКА РАВНАПОЛОВИНЕ ПРОИЗВЕДЕНИЯ ЕГО ОСНОВАНИЯ
НА ВЫСОТУ.
С
D Дано: АВС;
СН- высота;
АВ- основание.
Док-ть: S= ½ АВ СН.
А
Н
В
Док-во: АВС= DСВ (по трем сторонам (СВ- общая, АВ=
СД, АС= ВД ))
SАВС =SDСВ
SАВС= ½ SАBCD, т.е. S = = ½ АВ СН.
Теорема доказана.
5
6. Следствие 1.
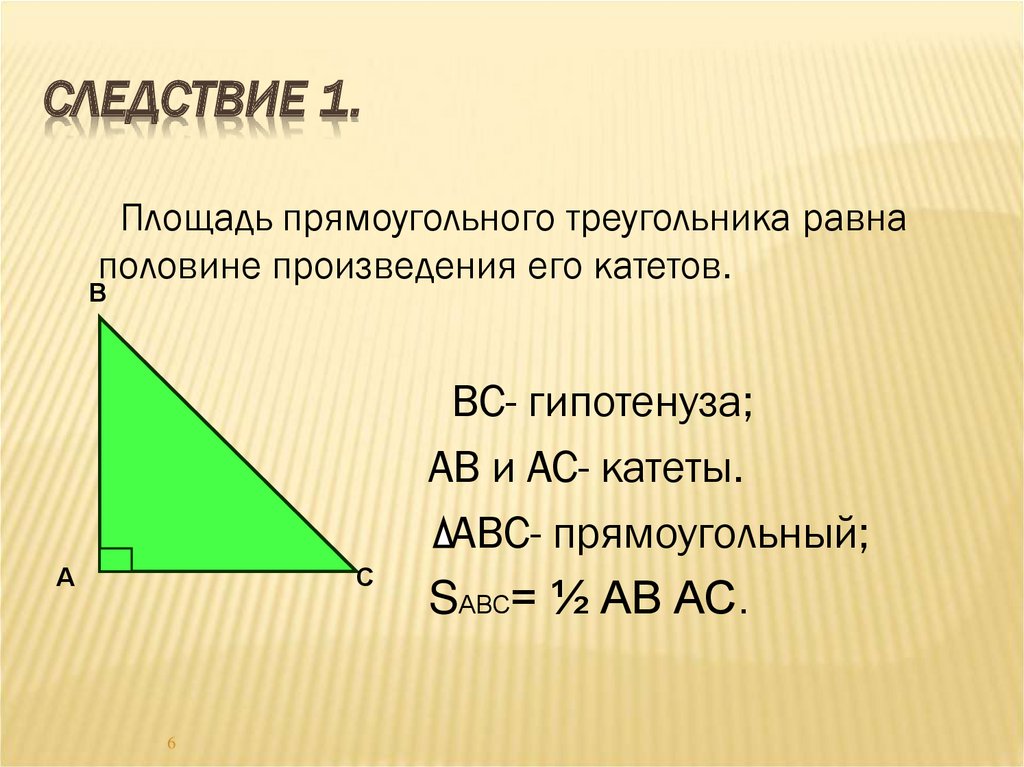
СЛЕДСТВИЕ 1.Площадь прямоугольного треугольника равна
половине произведения его катетов.
В
А
С
6
ВС- гипотенуза;
АВ и АС- катеты.
АВС- прямоугольный;
SАВС= ½ АВ АС.
7. Следствие 2.
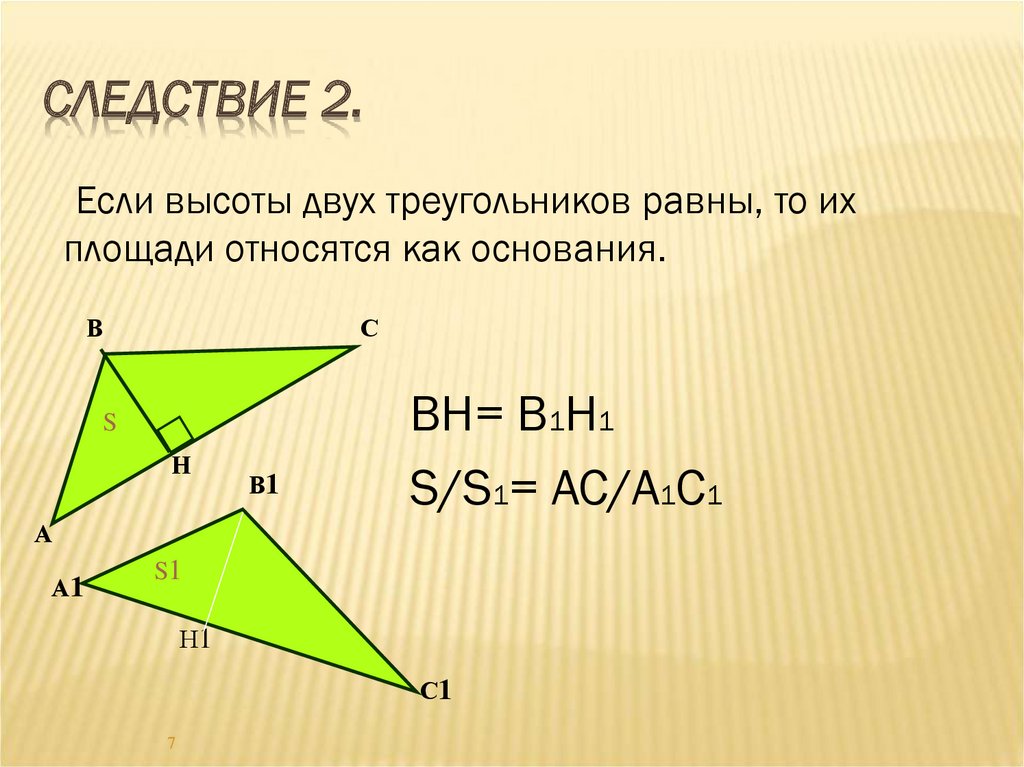
СЛЕДСТВИЕ 2.Если высоты двух треугольников равны, то их
площади относятся как основания.
В
С
S
Н
В1
ВН= В1Н1
S/S1= АС/А1С1
А
А1
S1
Н1
С1
7
8.
1.Дано:
Найти:
ABCD параллелограмм
S ABD
C
B
4
А
D
9.
2.Дано:
Найти:
ABC треугольник
S ABС
B
300
А
9см
С
10.
11.
ВА
С
Н
Н
D
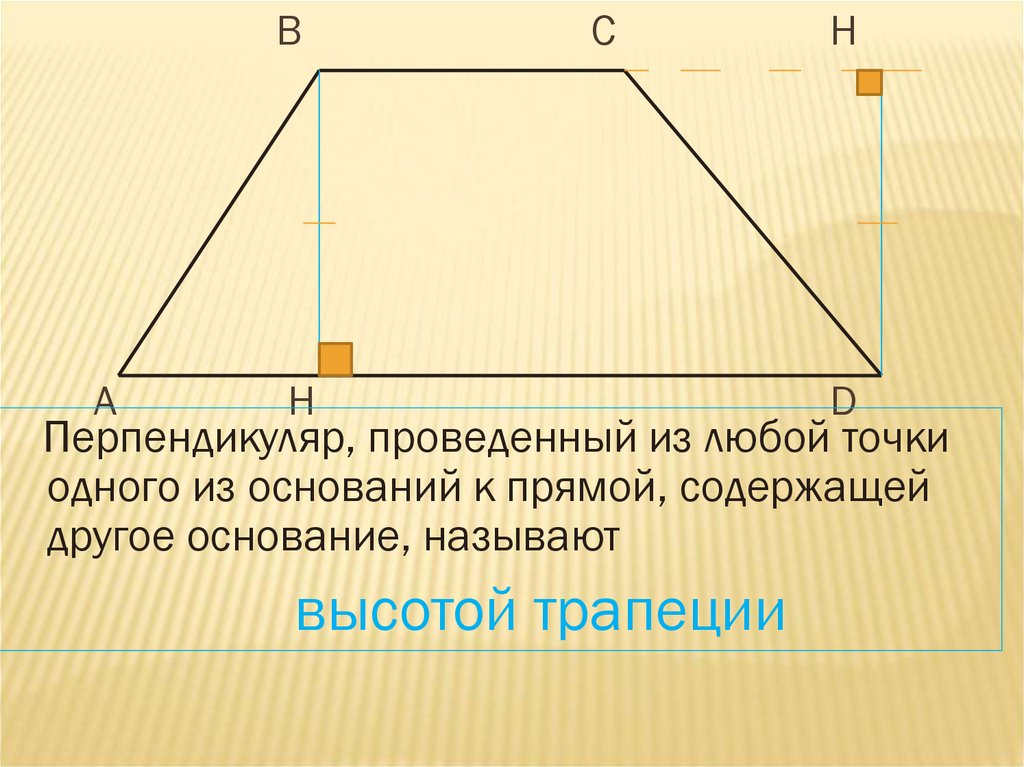
Перпендикуляр, проведенный из любой точки
одного из оснований к прямой, содержащей
другое основание, называют
высотой трапеции
12. Теорема: Площадь трапеции равна произведению полусуммы ее оснований на высоту.
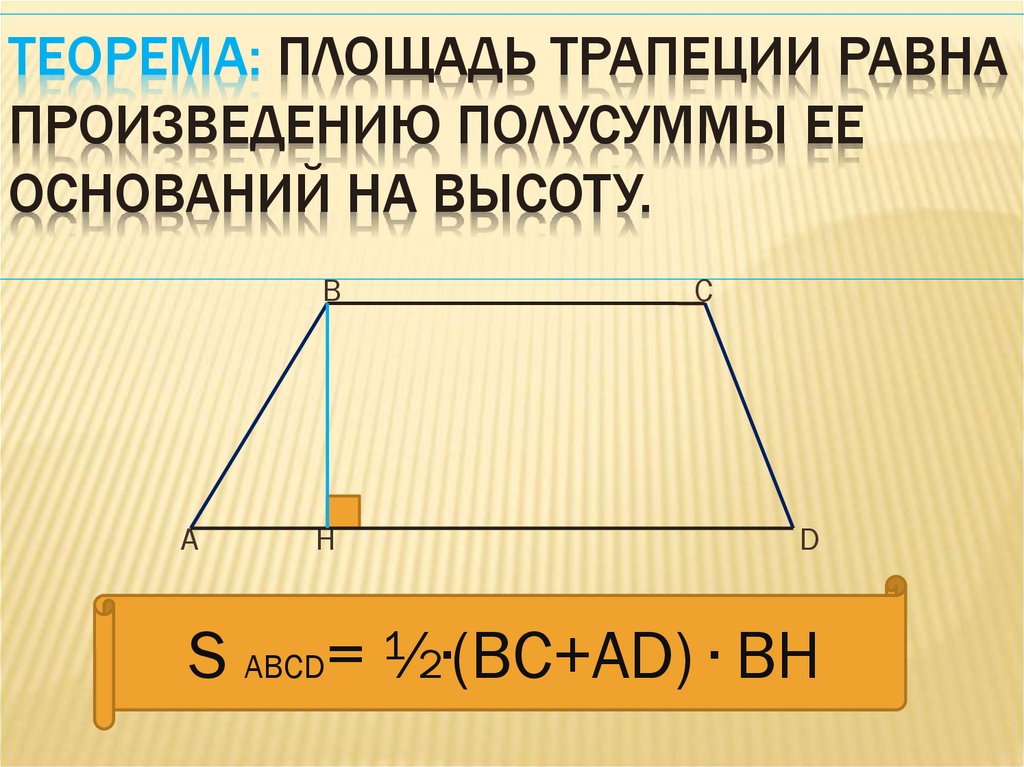
ТЕОРЕМА: ПЛОЩАДЬ ТРАПЕЦИИ РАВНАПРОИЗВЕДЕНИЮ ПОЛУСУММЫ ЕЕ
ОСНОВАНИЙ НА ВЫСОТУ.
В
А
Н
С
D
S ABCD= ½∙(BC+AD) ∙ ВН
13.
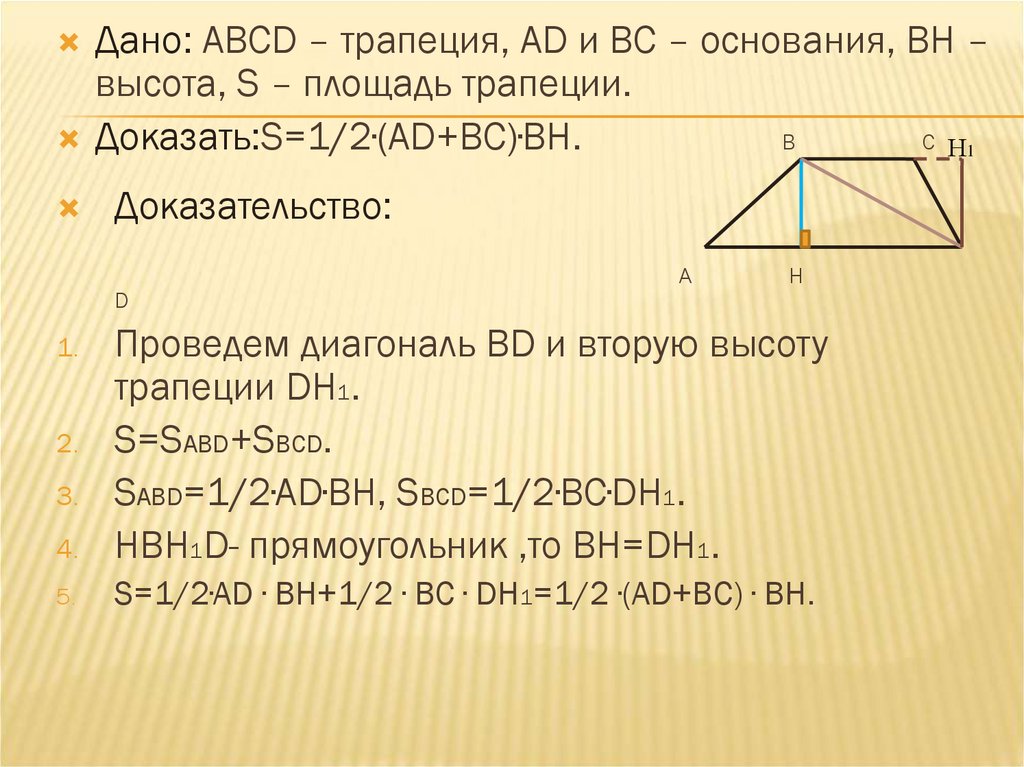
Дано: АВСD – трапеция, АD и ВС – основания, ВН –высота, S – площадь трапеции.
Доказать:S=1/2∙(AD+BC)∙BН.
В
С Н1
Доказательство:
D
А
Н
4.
Проведем диагональ ВD и вторую высоту
трапеции DН1.
S=SABD+SBCD.
SABD=1/2∙AD∙BH, SBCD=1/2∙BC∙DH1.
HBH1D- прямоугольник ,то BH=DH1.
5.
S=1/2∙AD ∙ BH+1/2 ∙ BC ∙ DH1=1/2 ∙(AD+BC) ∙ BH.
1.
2.
3.
14. Решить задачу
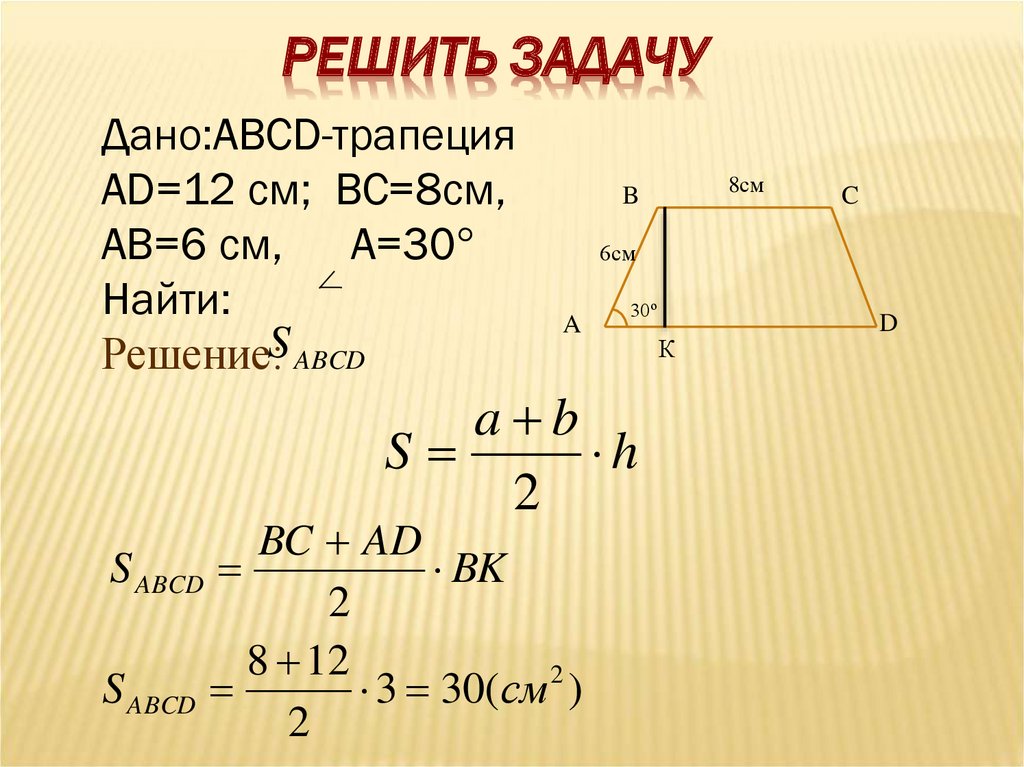
РЕШИТЬ ЗАДАЧУДано:ABCD-трапеция
AD=12 см; BC=8см,
AB=6 см, A=30°
Найти:
Решение:S ABCD
8см
B
C
6см
A
30º
a b
S
h
2
BC AD
S ABCD
BK
2
8 12
2
S ABCD
3 30( см )
2
К
D







 mathematics
mathematics








