Similar presentations:
Площадь треугольника
1.
15.11.2022Классная работа
2. ВЕРНО ЛИ, ЧТО
1. Площадь параллелограмма равна произведению егосторон
2. Катет, противолежащий углу в 300 равен половине
гипотенузы
3. Сумма острых углов прямоугольного треугольника
равна 900
4. Равные многоугольники имеют равные площади
5. Чтобы найти площадь квадрата, надо его сторону
умножить на 4
3.
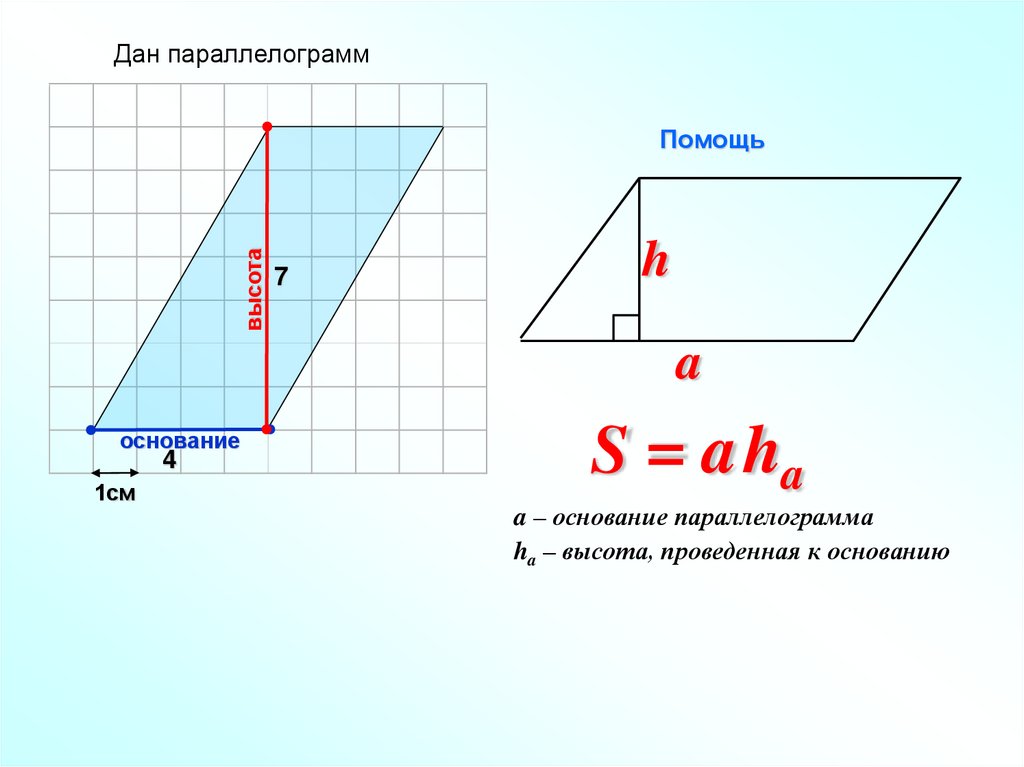
Дан параллелограммвысота
Помощь
7
h
a
основание
4
1см
S = a ha
a – основание параллелограмма
ha – высота, проведенная к основанию
4.
АBCD - параллелограммНайти площадь параллелограмма.
В
С
4
2
А
D
K
5.
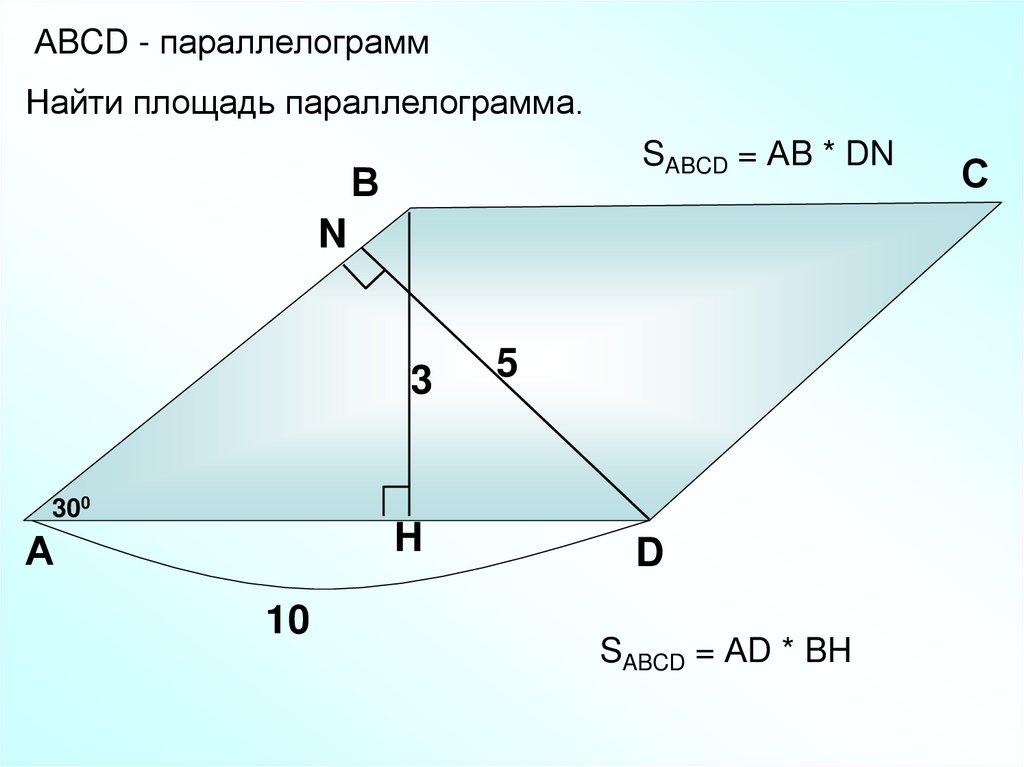
АBCD - параллелограммНайти площадь параллелограмма.
SABCD = АB * DN
В
N
3
5
300
H
А
10
D
SABCD = АD * BH
С
6.
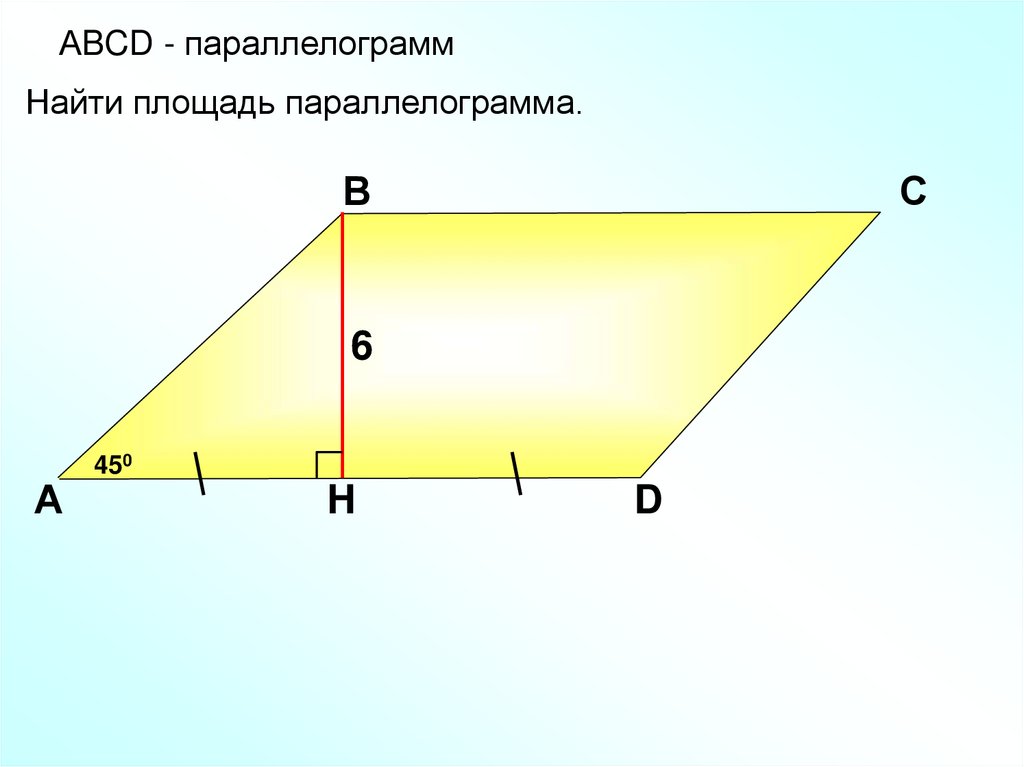
АBCD - параллелограммНайти площадь параллелограмма.
В
С
6
А
450
H
D
7.
ВН1
А
Н
С
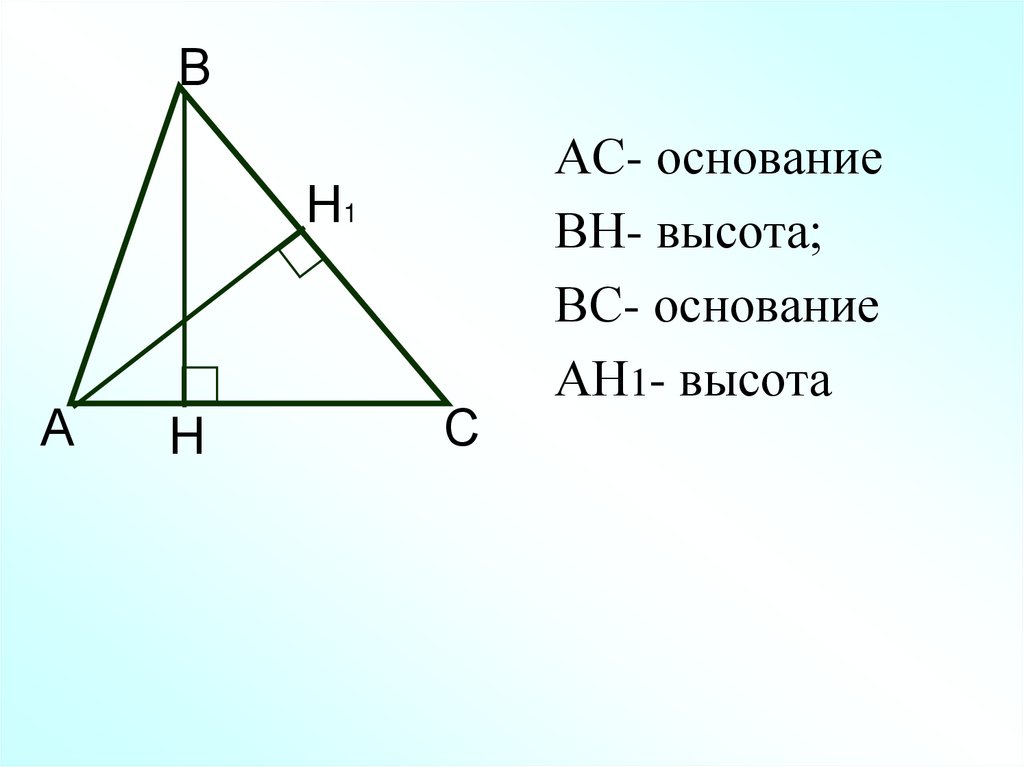
АС- основание
ВН- высота;
ВС- основание
АН1- высота
8.
Найти площадь треугольника.В
2
А
H
5
С
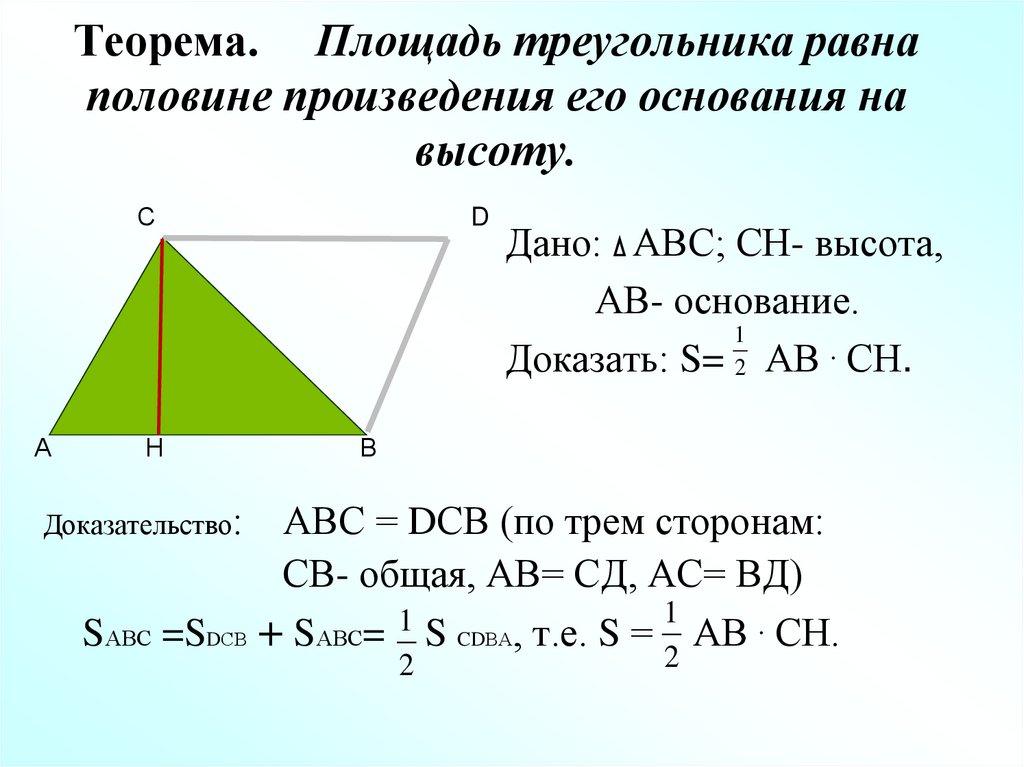
9. Теорема. Площадь треугольника равна половине произведения его основания на высоту.
СА
Н
D
Дано: АВС; СН- высота,
АВ- основание.
1
Доказать: S= 2 АВ . СН.
В
Доказательство:
АВС = DСВ (по трем сторонам:
СВ- общая, АВ= СД, АС= ВД)
1
1
SАВС =SDСВ + SАВС= S CDВА, т.е. S = АВ . СН.
2
2
10.
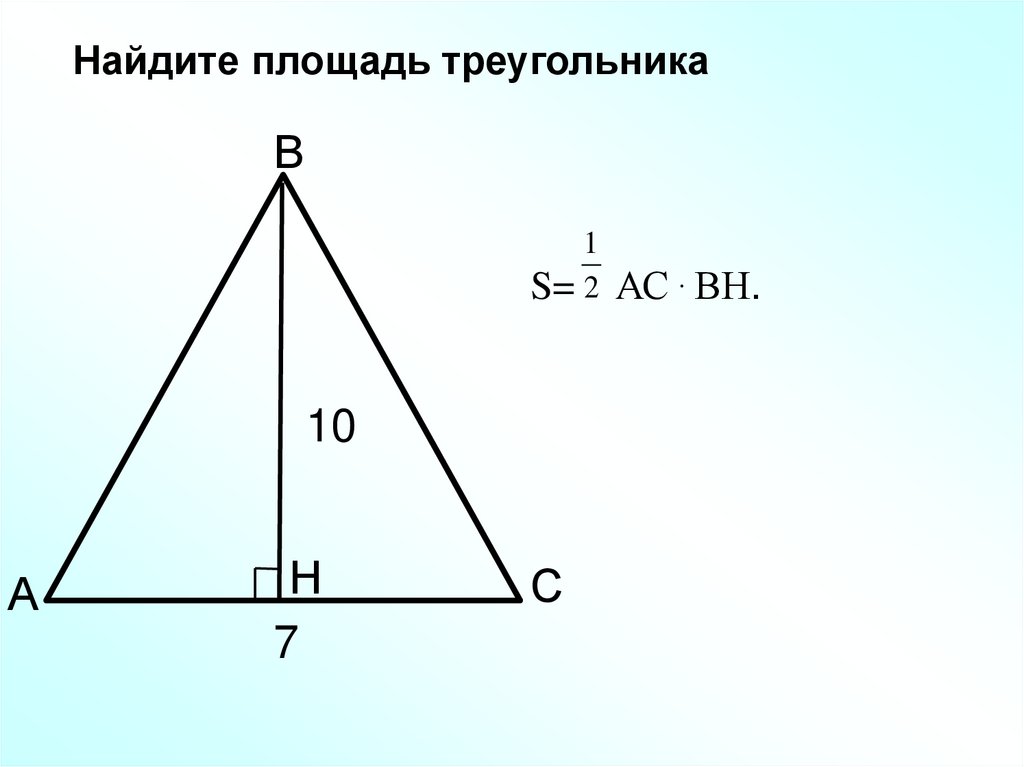
Найдите площадь треугольникаВ
1
S= 2 АС . ВН.
10
А
Н
7
С
11.
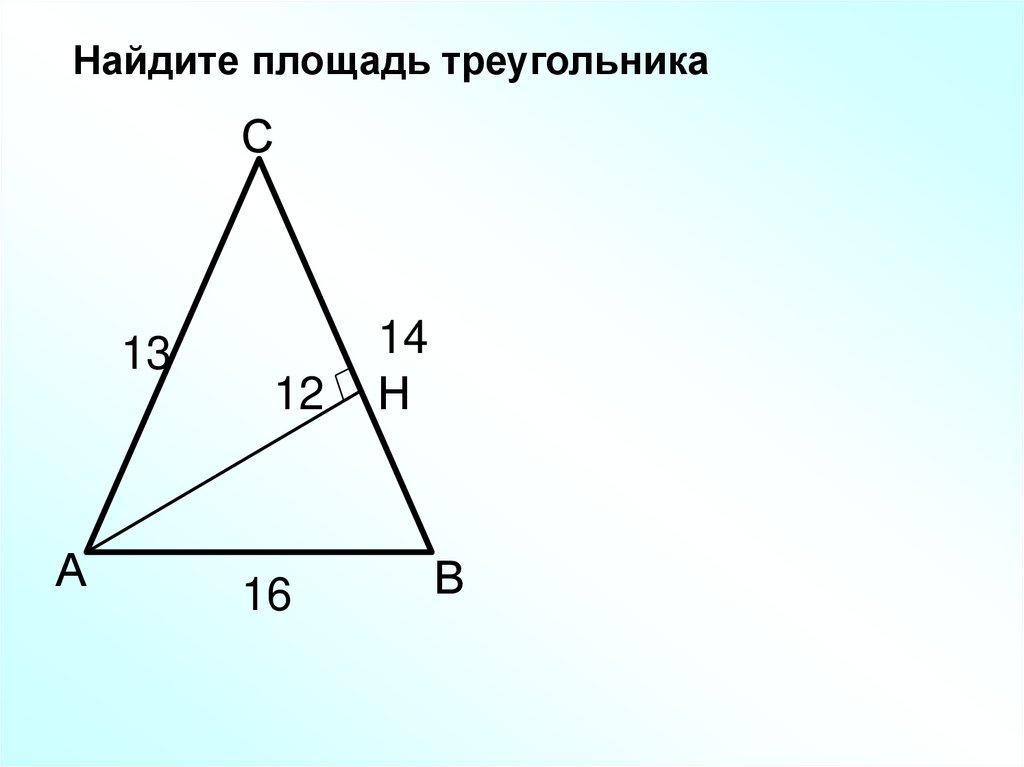
Найдите площадь треугольникаС
13
А
12
16
14
Н
В
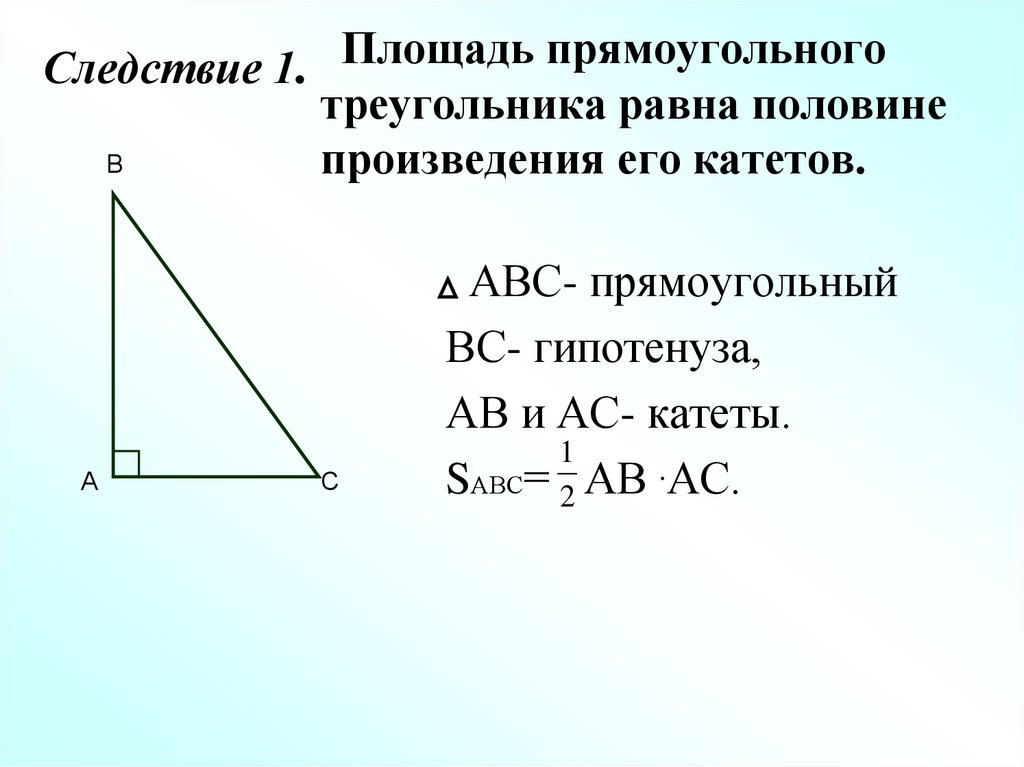
12. Следствие 1.
Площадь прямоугольноготреугольника равна половине
В
произведения его катетов.
А
С
АВС- прямоугольный
ВС- гипотенуза,
АВ и АС- катеты.
1
SАВС= 2 АВ .АС.
13.
Найдите площадь треугольникаМ
15
17
К
А
8
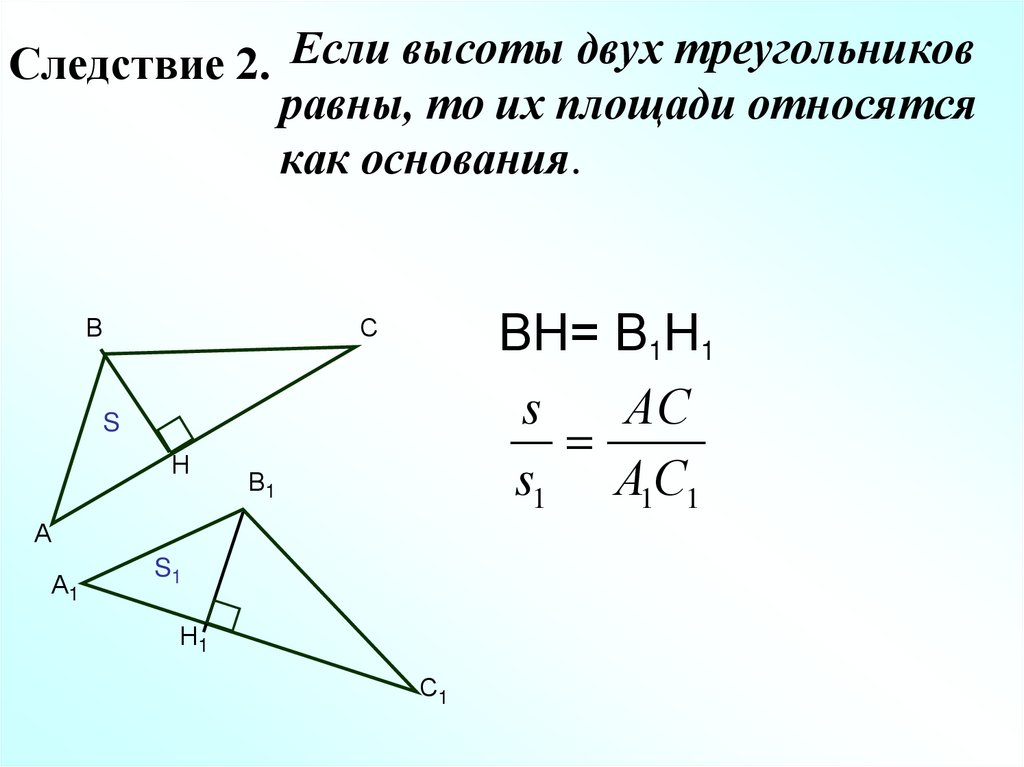
14. Следствие 2.
Если высоты двух треугольниковравны, то их площади относятся
как основания.
В
ВН= В1Н1
s
АС
s1 А1С1
С
S
Н
В1
А
А1
S1
Н1
С1
15. Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как
произведения сторон, заключающих равные углы.С
А
С1
S
В
А1
С1
Н
s1
S1
В1
S АВ1С
В1
В
А1В1С1; <А= < А1.
АС АВ
А1С1 А1 В1
Доказательство:
Наложим А1В1С1 на АВС,
АВС и АВ1С имеют общую высоту СН,
S
Н1
С
А(А1)
Дано: АВС и
Доказать: s
АВ
АВ1
Треугольники АВ1С и АВ1С1 имеют общую высоту –
АС
В1SНАВ1 1С
перемножая равенства,
s
АС получаем:
АВ
S АВ1С 1 АС1
s1
А1С1 А1 В1
16.
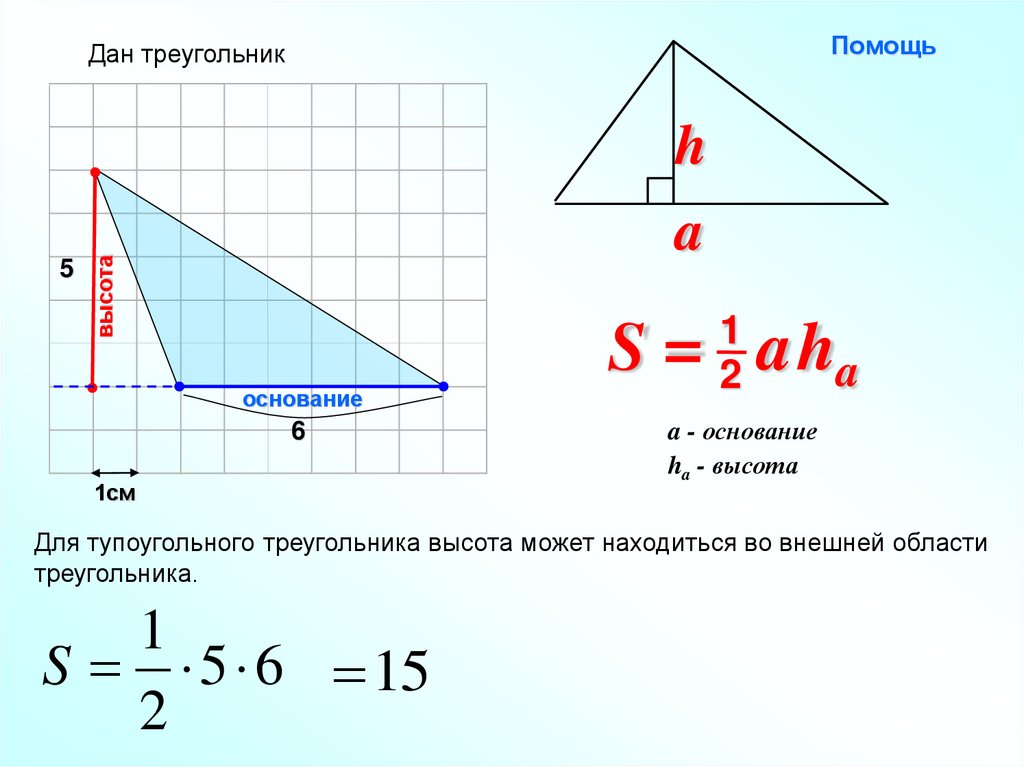
ПомощьДан треугольник
h
высота
5
a
основание
6
1см
1
2
S = aha
a - основание
ha - высота
Для тупоугольного треугольника высота может находиться во внешней области
треугольника.
1
S 5 6 15
2
17.
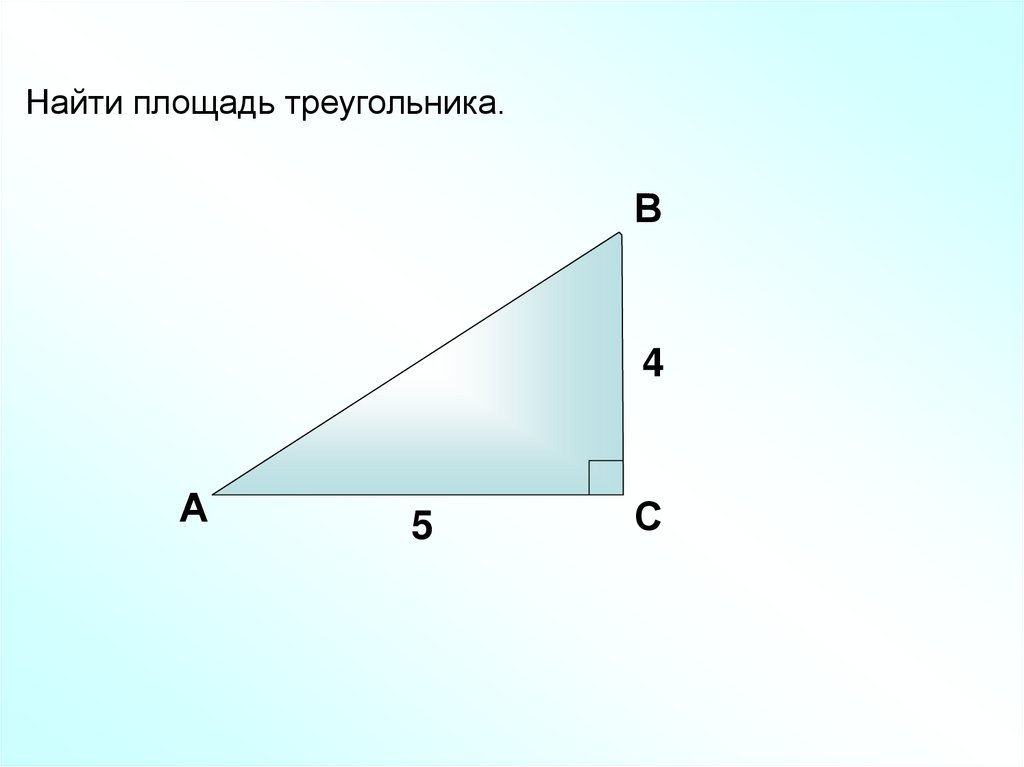
Найти площадь треугольника.В
4
А
5
С
18.
ВЫ
С
О
Т
А
1
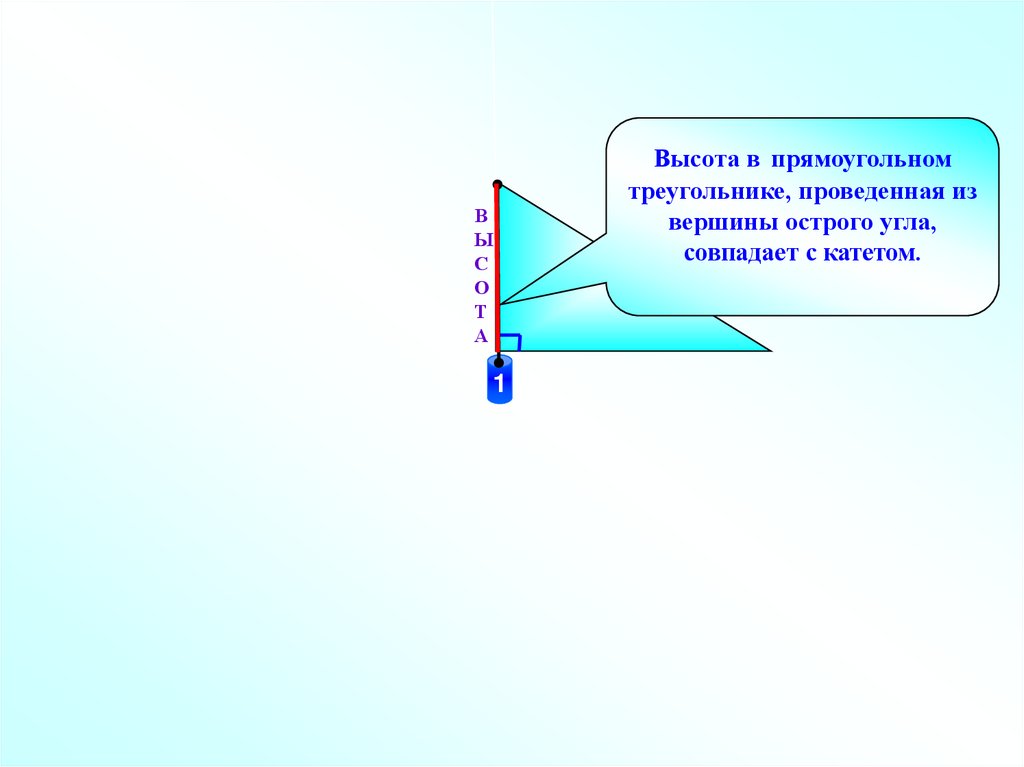
Высота в прямоугольном
треугольнике, проведенная из
вершины острого угла,
совпадает с катетом.
19.
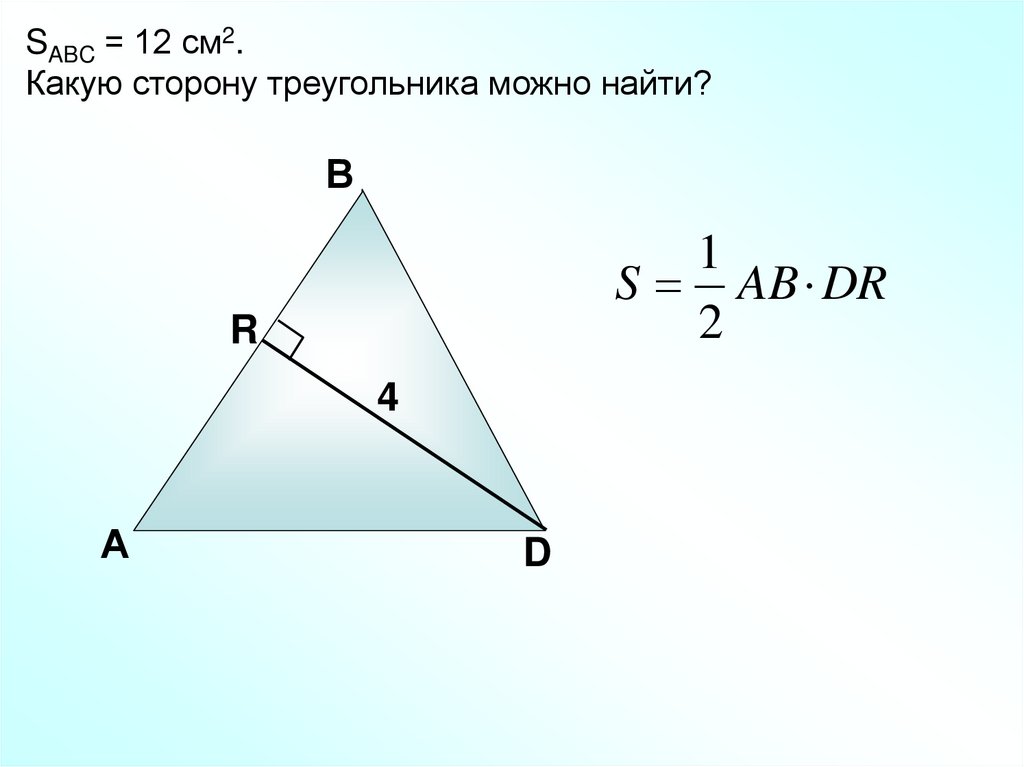
SABC = 12 см2.Какую сторону треугольника можно найти?
В
1
S AB DR
2
R
4
А
D






 mathematics
mathematics








