Площадь треугольника

1. Площадь треугольника

2.

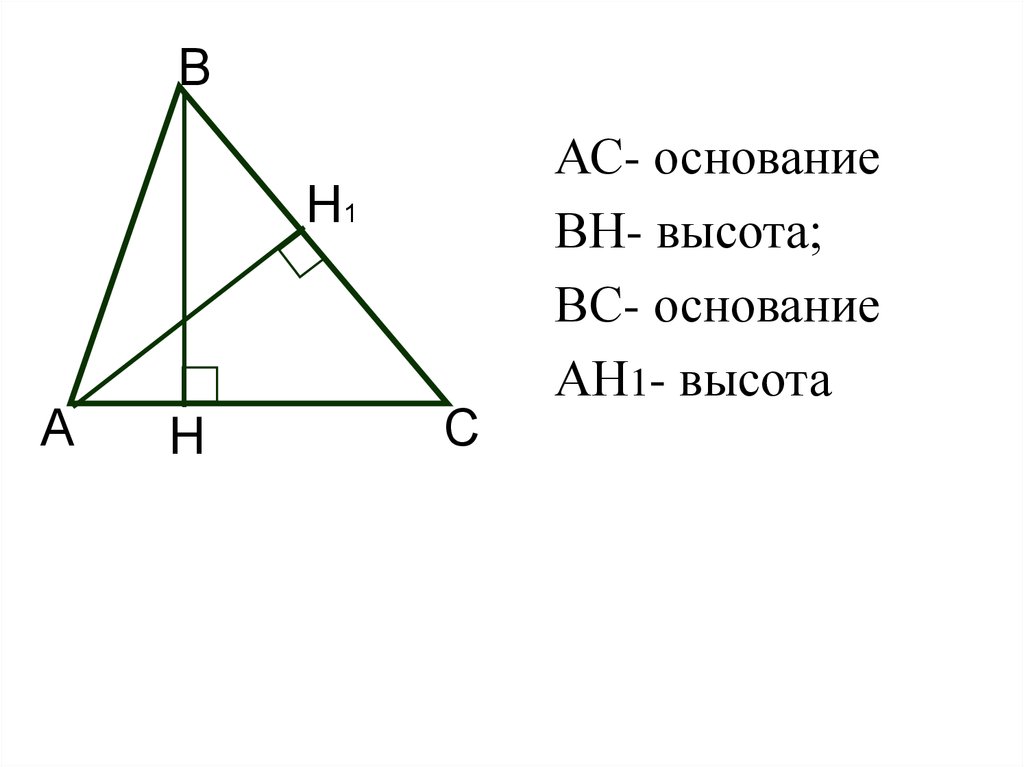
В
Н1
А
Н
С
АС- основание
ВН- высота;
ВС- основание
АН1- высота

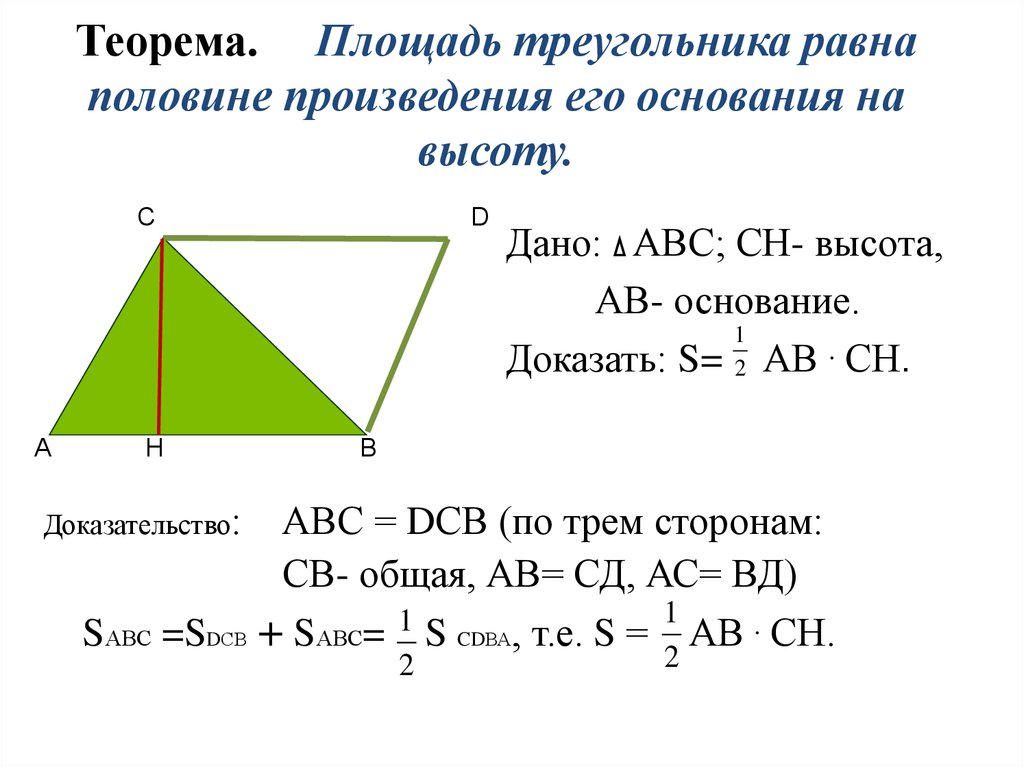
3. Теорема. Площадь треугольника равна половине произведения его основания на высоту.

С
А
Н
D
Дано: АВС; СН- высота,
АВ- основание.
1
Доказать: S= 2 АВ . СН.
В
Доказательство:
АВС = DСВ (по трем сторонам:
СВ- общая, АВ= СД, АС= ВД)
1
1
SАВС =SDСВ + SАВС= S CDВА, т.е. S = АВ . СН.
2
2

4.

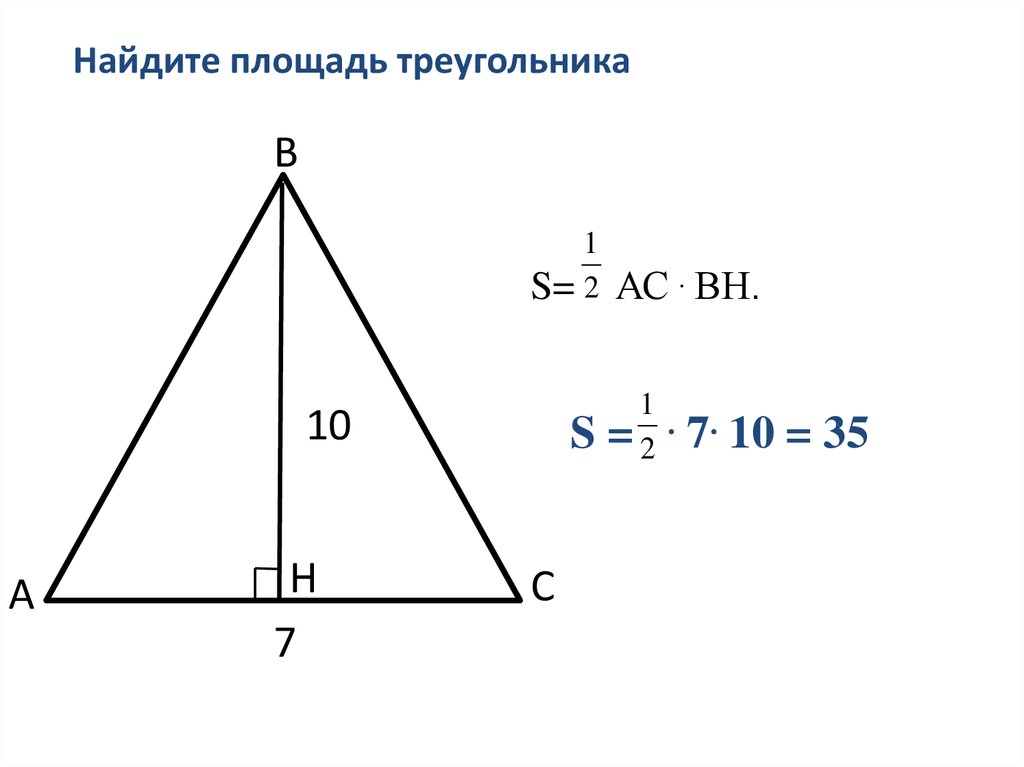
Найдите площадь треугольника
В
1
S= 2
10
А
Н
7
S
С
АС . ВН.
1
=2 .
7. 10 = 35

5.

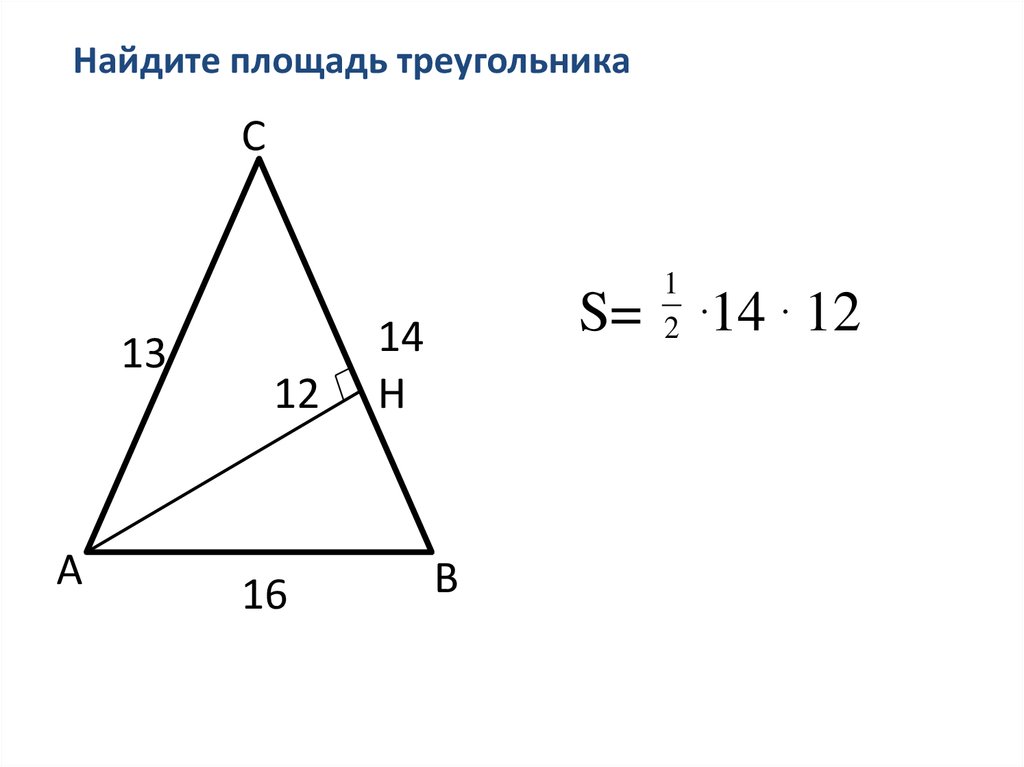
Найдите площадь треугольника
С
13
А
12
16
S=
14
Н
В
1
2
.14 .
12

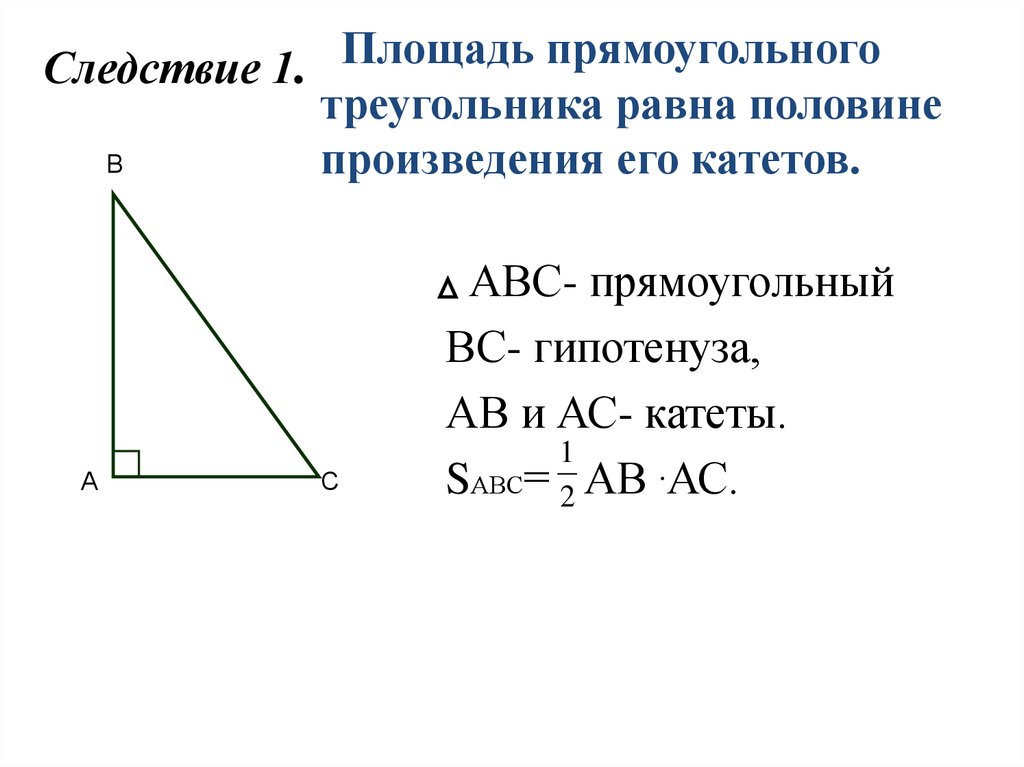
6. Следствие 1.

Площадь прямоугольного
треугольника равна половине
В
произведения его катетов.
А
С
АВС- прямоугольный
ВС- гипотенуза,
АВ и АС- катеты.
1
SАВС= 2 АВ .АС.

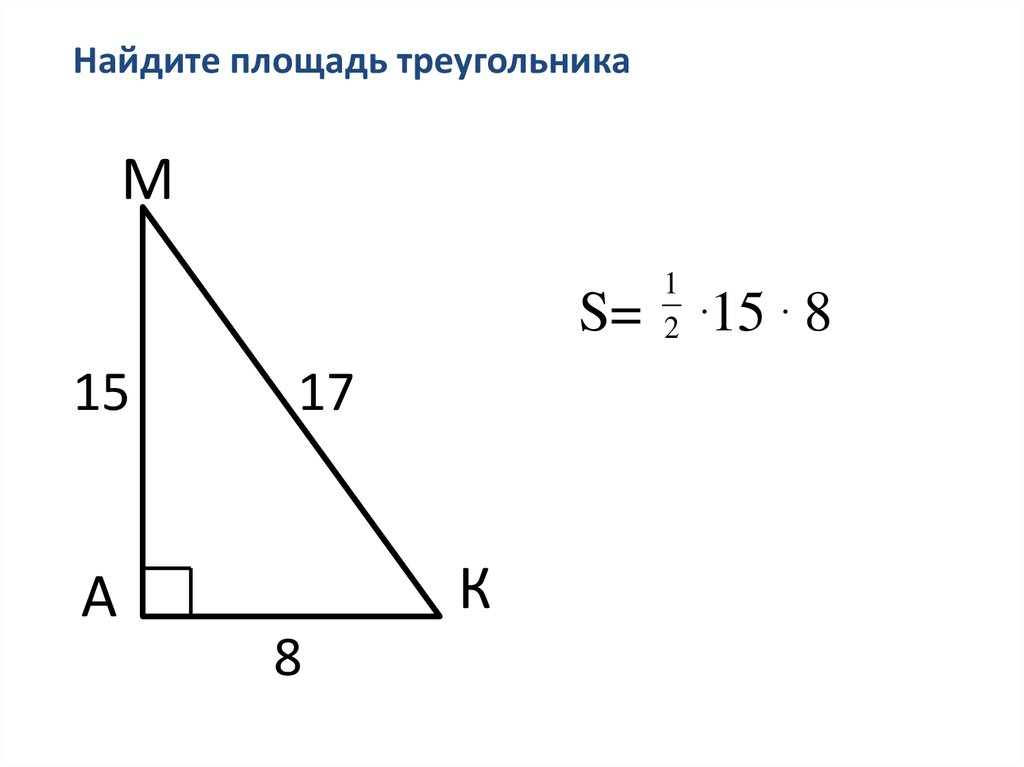
7.

Найдите площадь треугольника
М
S=
15
17
К
А
8
1
2
.15 .
8

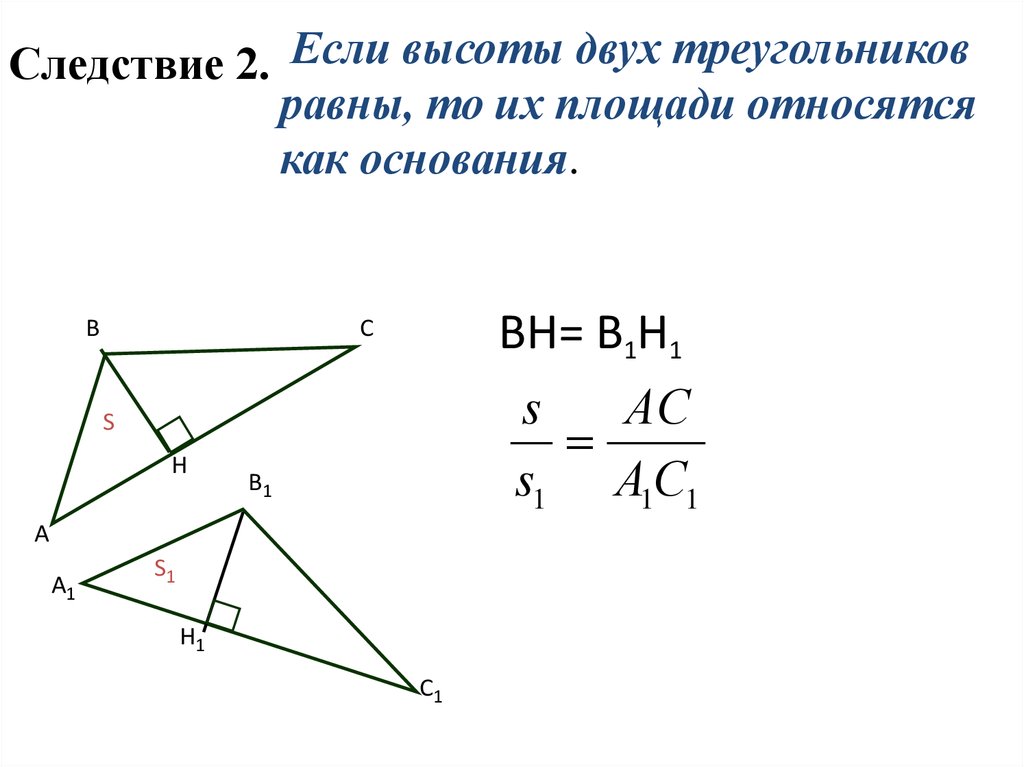
8. Следствие 2.

Если высоты двух треугольников
равны, то их площади относятся
как основания.
В
ВН= В1Н1
s
АС
s1 А1С1
С
S
Н
В1
А
А1
S1
Н1
С1

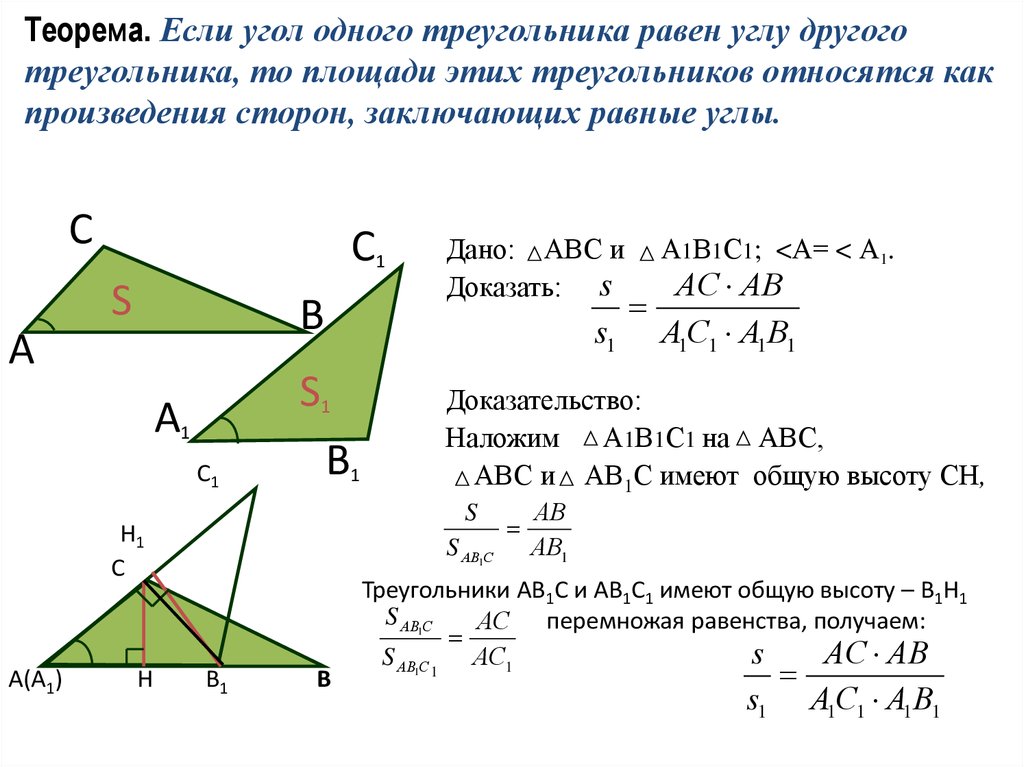
9. Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как

произведения сторон, заключающих равные углы.
С
С1
S
В
А
А1
С1
S1
В1
Н
s1
S АВ1С
В1
В
А1В1С1; <А= < А1.
АС АВ
А1С1 А1 В1
Доказательство:
Наложим А1В1С1 на АВС,
АВС и АВ1С имеют общую высоту СН,
S
Н1
С
А(А1)
Дано: АВС и
Доказать: s
АВ
АВ1
Треугольники АВ1С и АВ1С1 имеют общую высоту – В1Н1
S АВ1С
АС перемножая равенства, получаем:
s
АС АВ
S АВ1С 1 АС1
s1
А1С1 А1 В1