Similar presentations:
Площадь треугольника
1. Площадь треугольника
ПЛОЩАДЬТРЕУГОЛЬНИКА
Автор:
Сидорова А.В.
учитель математики
МБОУ СОШ № 31
г.Мурманска
2. Устно
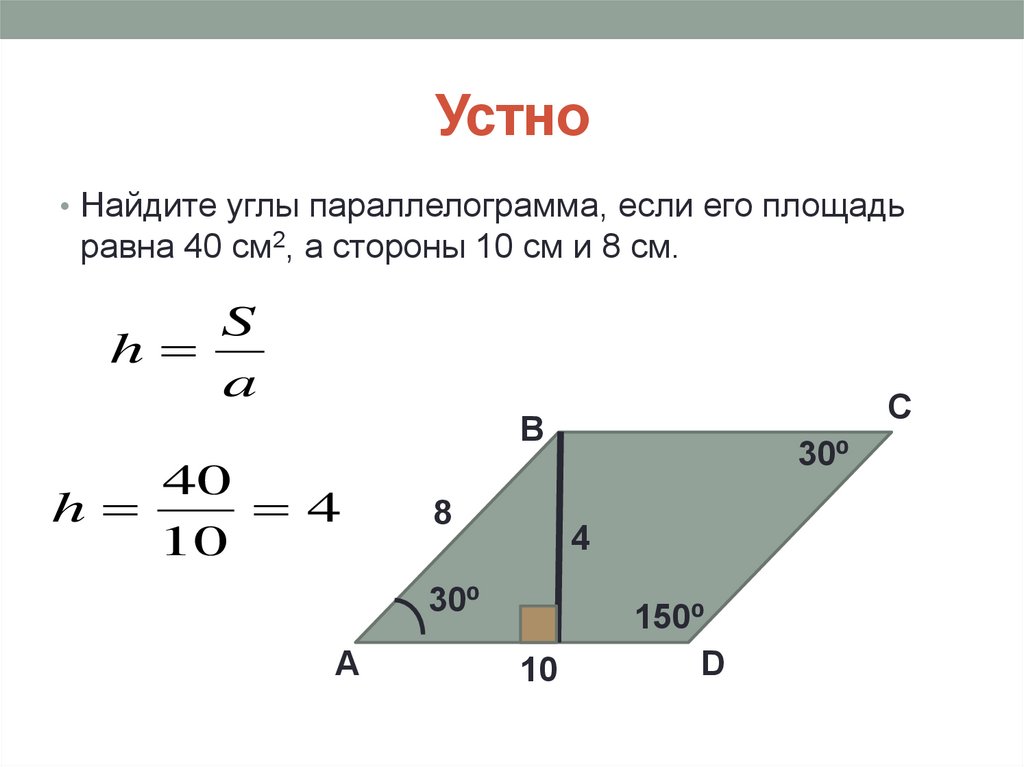
• Найдите углы параллелограмма, если его площадьравна 40 см2, а стороны 10 см и 8 см.
S
h
a
C
B
40
h
4
10
8
4
30⁰
А
30⁰
10
150⁰
D
3. Теорема
• Площадь треугольника равна половине произведенияего основания на высоту.
В
А
Н С
D
Дано:
∆АВС
ВН= h – высота
АС = а – основание
Доказать:
1
S
ah
2
4. Следствие 1
• Площадь прямоугольного треугольника равнаполовине произведения его катетов.
В
1
S
ab
2
h
b
С
а
А
5. Следствие 2
• Если высоты двух треугольников равны, то ихплощади относятся как основания.
h1 h2
h1
h2
a1
S1
S2
a2
1
a1h1
a1
2
1
a
2
a2 h2
2
6. Устно
BВ
30⁰
S-?
С
12
6
8
S-?
45⁰
А
С
A
7. Устно
С• Дано: ∆АВС, СМ – медиана ∆АВС
• СК – медиана ∆АСМ
• Найти:
А
К
М
В
S ACM S ACM S ACK
,
,
S ABC S BCK S BCK
8. Устно
CK
D
А
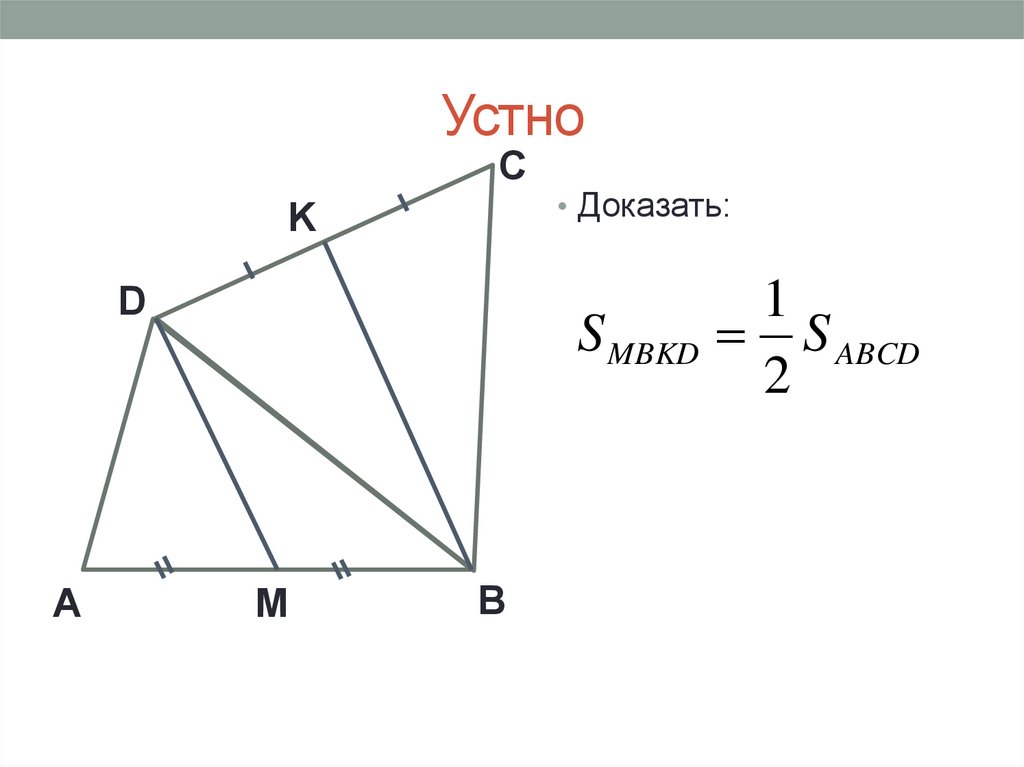
• Доказать:
S MBKD
M
B
1
S ABCD
2
9. Теорема
• Если угол одного треугольника равен углудругого треугольника, то площади этих
треугольников относятся как произведения
сторон, заключающих равные углы.
С1
Дано: ∆АВС и
∆А1В1С1
С
А А1
А
А1
В
В1 Доказать:
S1
AB AC
S 2 A1 B1 A1C1
10. Теорема
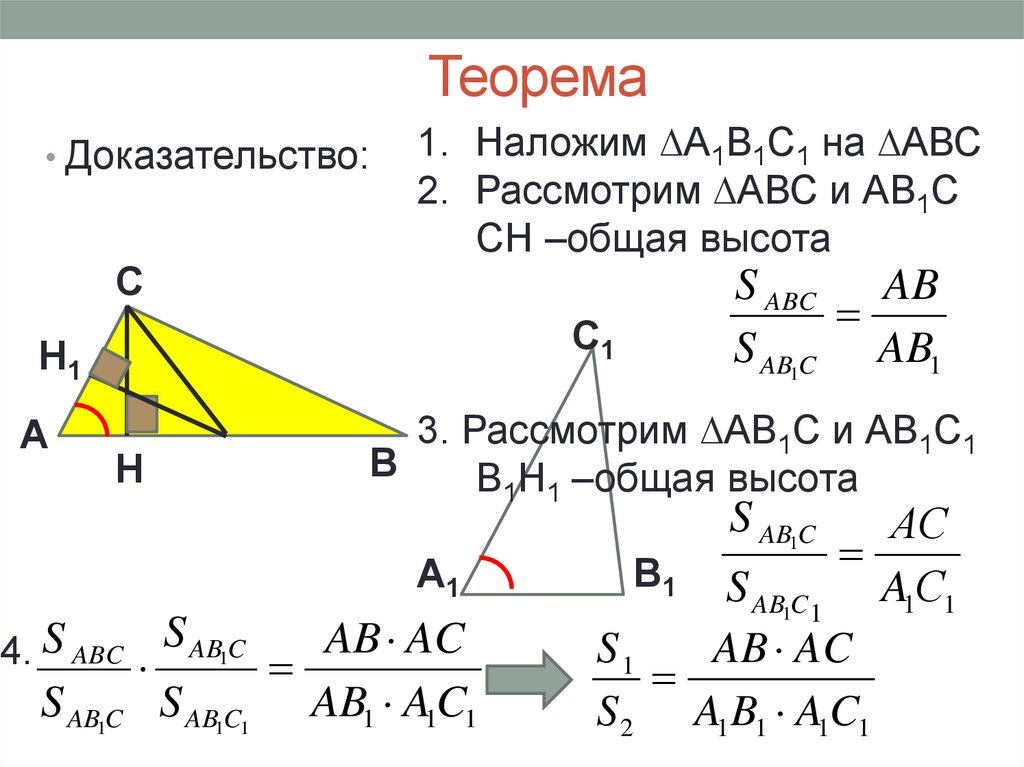
• Доказательство:С
1. Наложим ∆А1В1С1 на ∆АВС
2. Рассмотрим ∆АВС и АВ1С
СН –общая высота
С1
Н1
А
Н
3. Рассмотрим ∆АВ1С и АВ1С1
В
В1Н1 –общая высота
А1
4. S ABC S AB1C AB AC
S AB1C S AB1C1
S ABC
AB
S AB1C AB1
AB1 A1C1
AС
В1 S
A1С1
AB1C 1
S1
AB AC
S 2 A1 B1 A1C1
S AB1C







 mathematics
mathematics