Площадь треугольника. Отношение площадей треугольников, имеющих по равному углу

1.

Площадь треугольника.
Отношение площадей треугольников ,
имеющих по равному углу.

2. Цель урока

• 1. Доказать теорему об отношении
площадей треугольников, имеющих по
равному углу.
• 2. Рассмотреть её применение при решении
задач.

3.

План урока
1. Разминка: чтение конфигурации.
2. Проверка выполнения домашней работы.
3. Доказательство теоремы.
4. Решение задач.
5. Домашнее задание.

4.

В
Н
30о
А
D
8 см
С

5.

1
Дано:
B
АВС – прямоугольный
треугольник,
AB = 8 cм, В = 45о
Найти:
8
А
S (ABC)
C
Ответ: 32 см2

6.

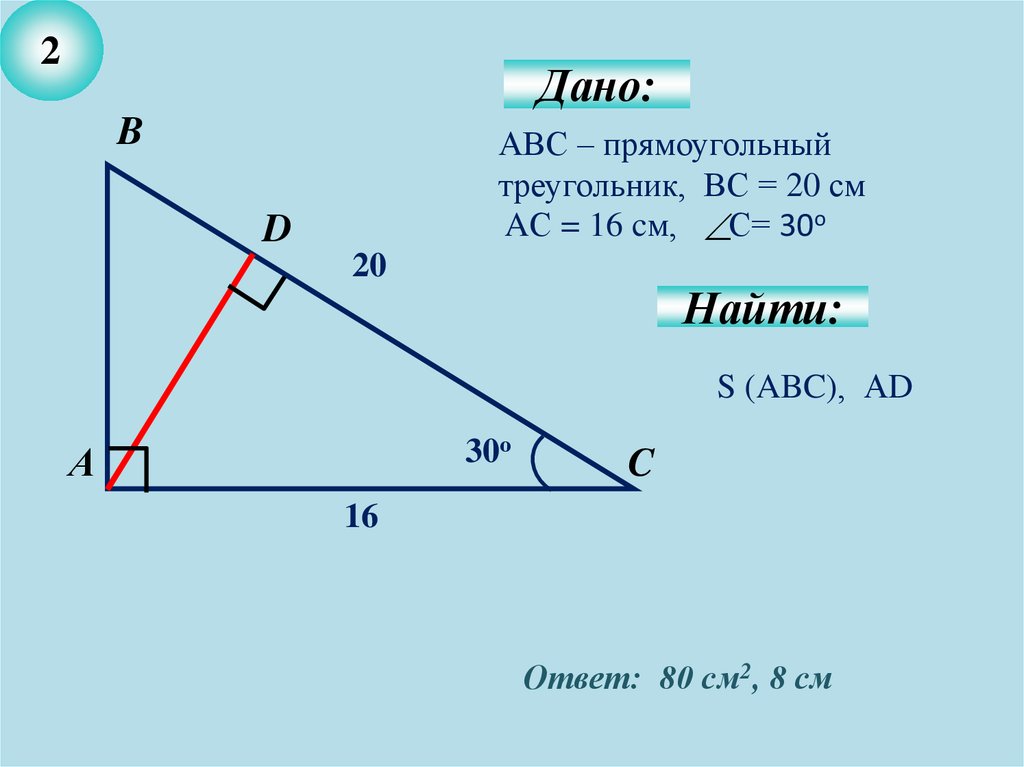
2
Дано:
B
АВС – прямоугольный
треугольник, ВС = 20 см
AС = 16 cм, С= 30о
D
20
Найти:
S (ABC), АD
30о
А
C
16
Ответ: 80 см2, 8 см

7.

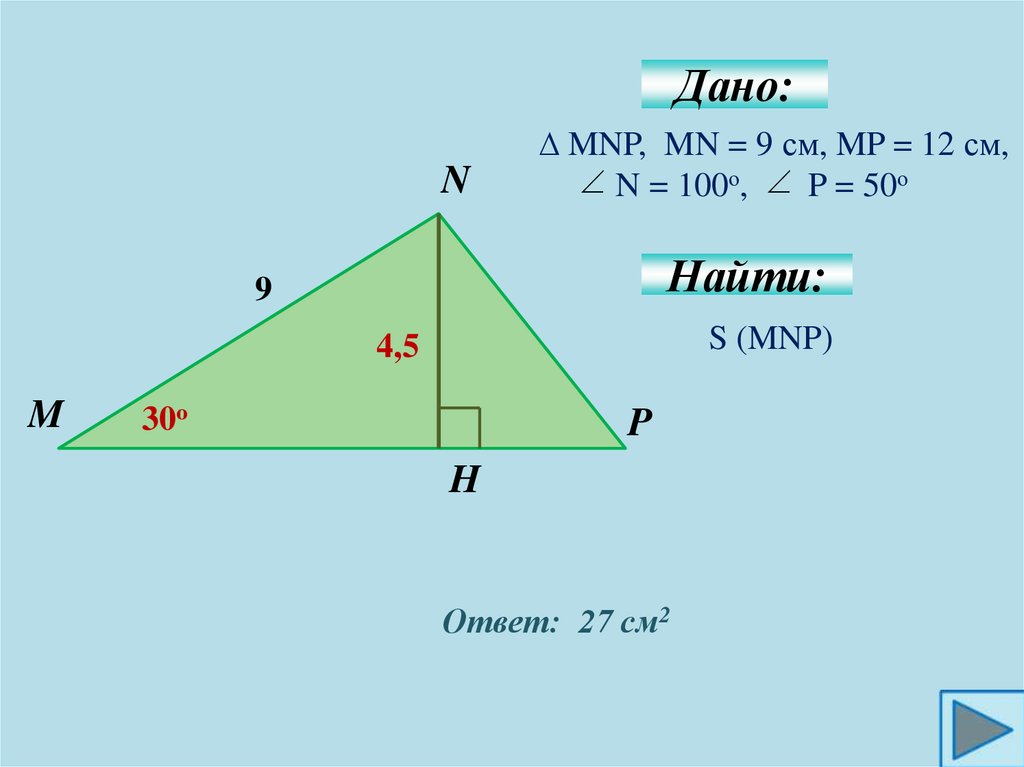
Дано:
N
∆ MNP, MN = 9 см, MP = 12 см,
N = 100о, P = 50о
Найти:
9
S (MNP)
4,5
M
30о
P
H
Ответ: 27 см2

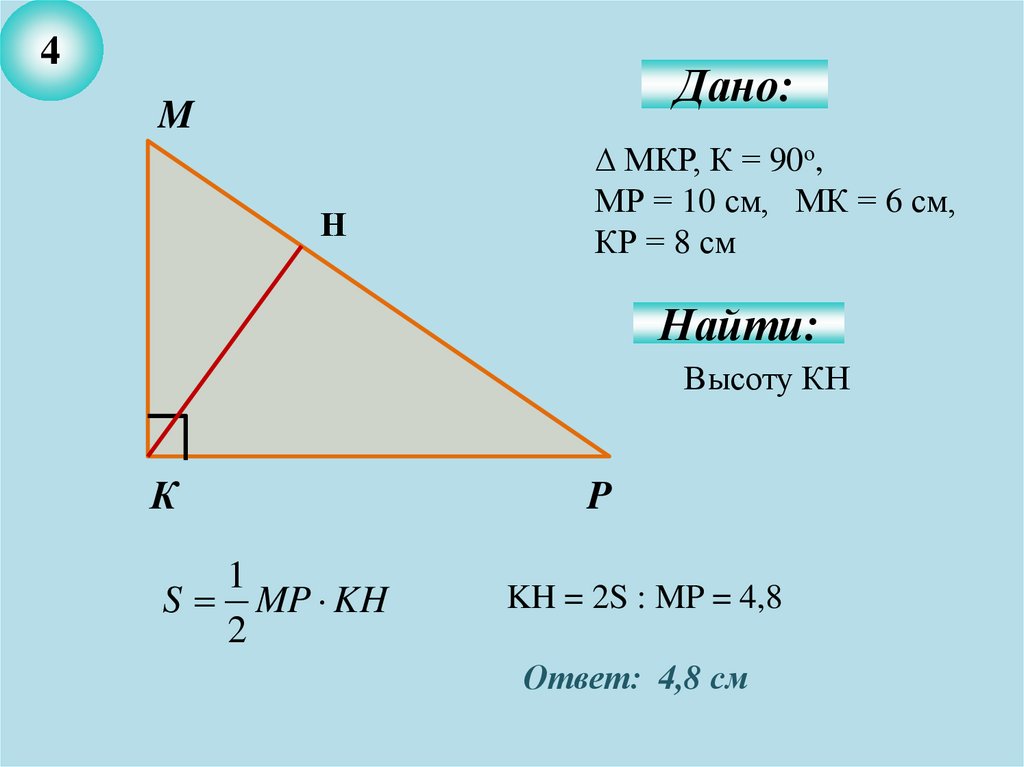
8.

4
Дано:
M
Н
∆ МКР, К = 90о,
МР = 10 см, МК = 6 см,
КР = 8 см
Найти:
Высоту КН
К
1
S MP KH
2
P
KH = 2S : MP = 4,8
Ответ: 4,8 см

9.

Равные основания
Равные высоты
S1= S2 = S3

10.

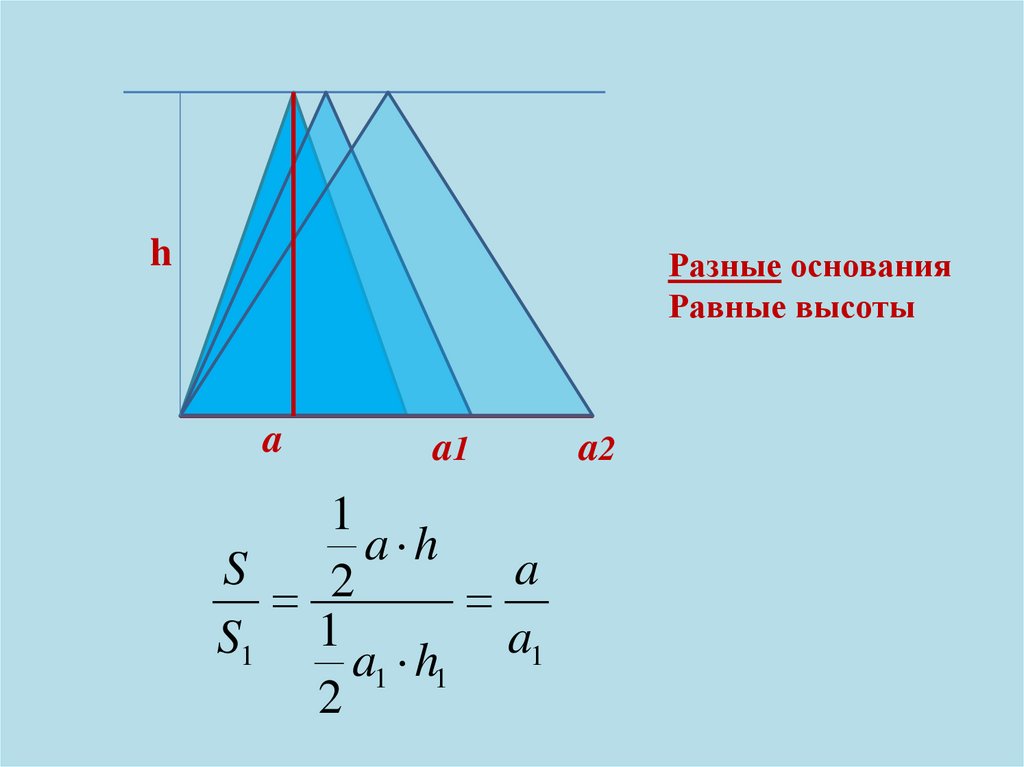
h
Разные основания
Равные высоты
a
a1
1
a h
S
a
2
S1 1 a h a1
1
1
2
a2

11.

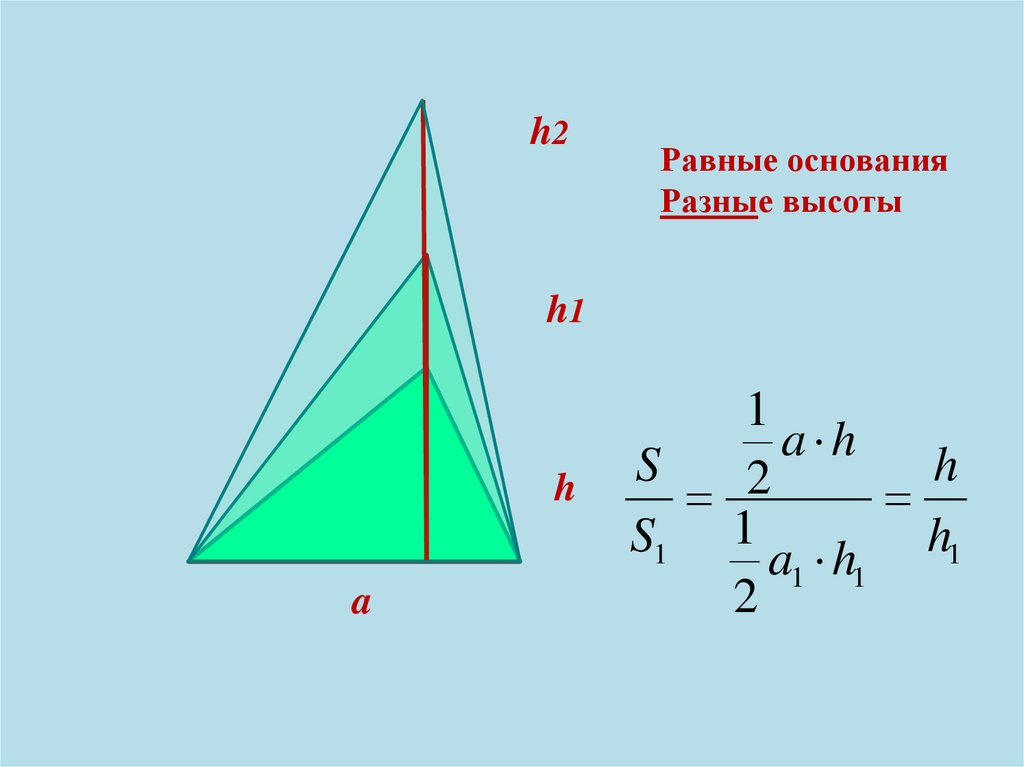
h2
Равные основания
Разные высоты
h1
h
a
1
a h
S
h
2
S1 1 a h h1
1
1
2

12.

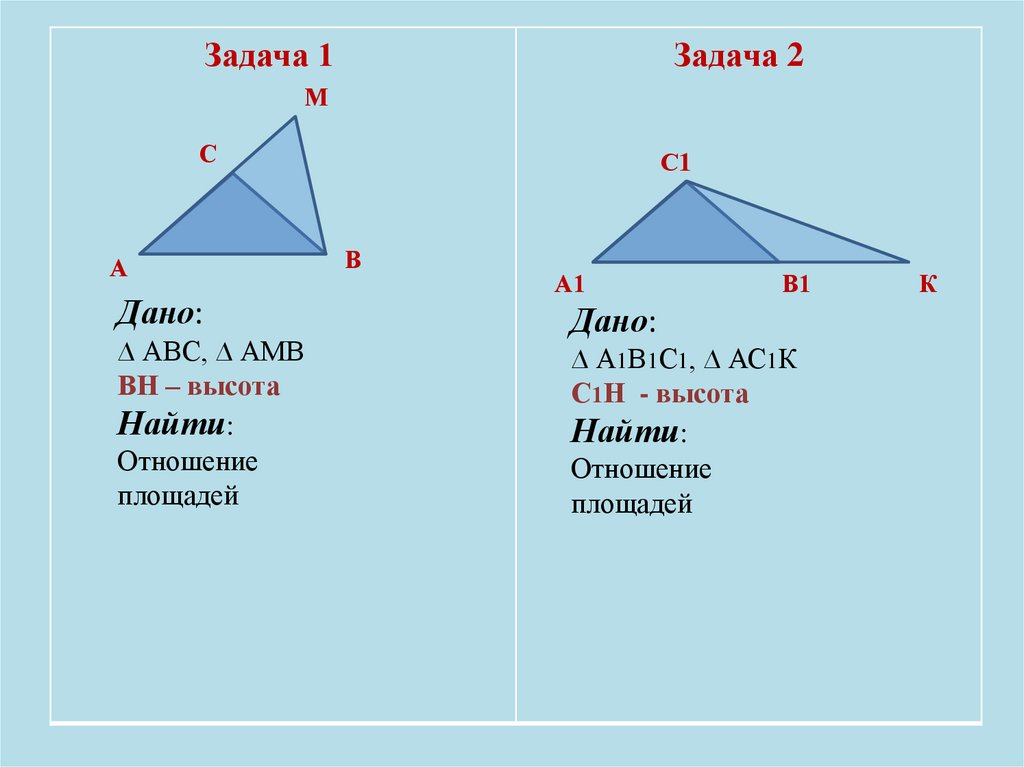
Задача 1
Задача 2
М
С
А
Дано:
∆ АВС, ∆ АМВ
ВН – высота
Найти:
Отношение
площадей
С1
В
А1
В1
Дано:
∆ А1В1С1, ∆ АС1К
С1Н - высота
Найти:
Отношение
площадей
К

13.

М
С
А
С1
В
А
А1
В1
М
С
А(А1)
В
К
К

14.

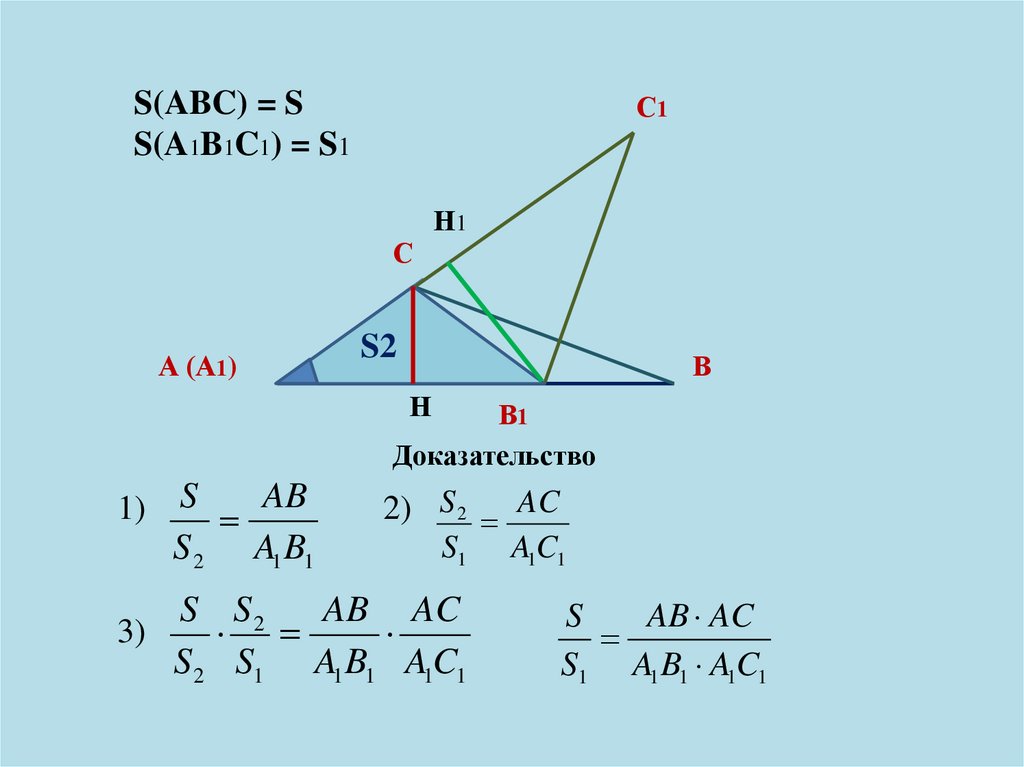
S(ABC) = S
S(A1B1C1) = S1
С1
Н1
С
S2
А (А1)
В
Н
В1
Доказательство
1) S AB
S2
3)
A1 B1
2) S 2 AC
S1
S S2
AB AC
S 2 S1 A1 B1 A1C1
A1C1
S
AB AC
S1 A1 B1 A1C1

15.

16. Итог урока.

3a
a
S
a
a
3a 3a
S1
=
=
a a
S
3a
S1
3a
9

17.

Домашнее задание:
1. п.52. Хорошо разобраться в
доказательстве теоремы.
2. Повторить доказательство
теорем о вычислении площади
параллелограмма и площади
треугольника.
3. № 479 (б).
4. По желанию: задача
«Куда делся квадратик?»