Similar presentations:
Площадь трапеции
1.
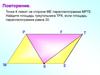
Повторение.Точка К лежит на стороне МЕ параллелограмма МРТЕ.
Найдите площадь треугольника ТРК, если площадь
параллелограмма равна 20.
Р
М
F
К
Т
Е
2.
Повторение.Найти SАВС
В
8
4
С
300
К
9
А
3.
Повторение.В
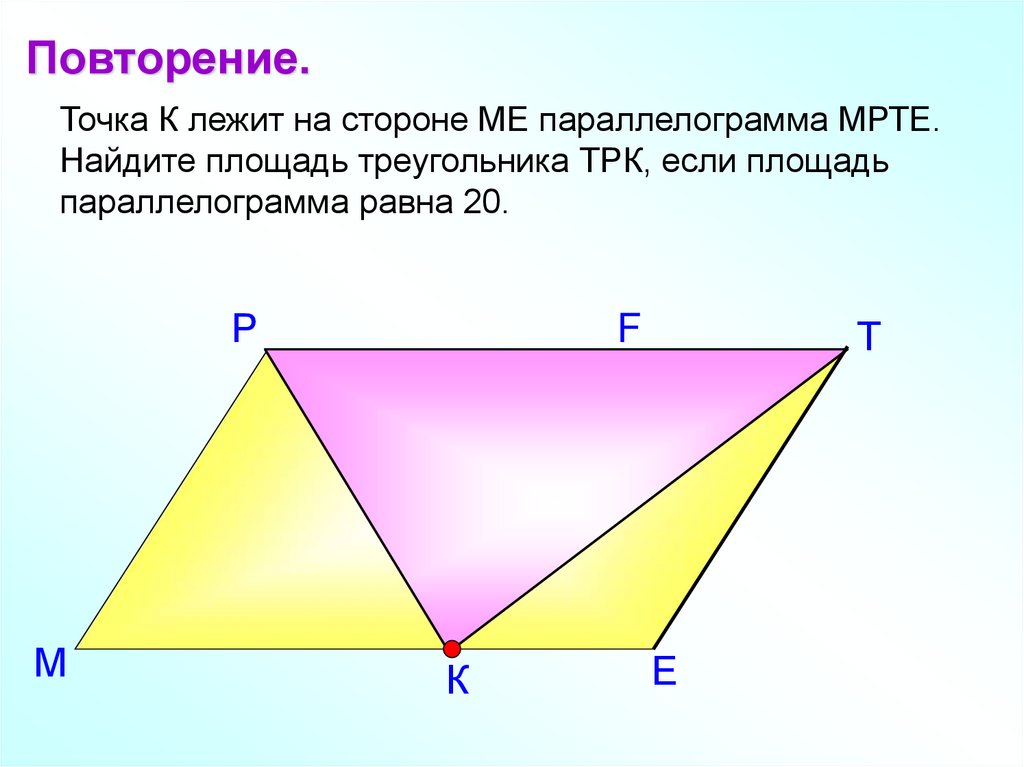
Найти SАВСK
С
К
5
4
А
D
1
52 4 5
2
4.
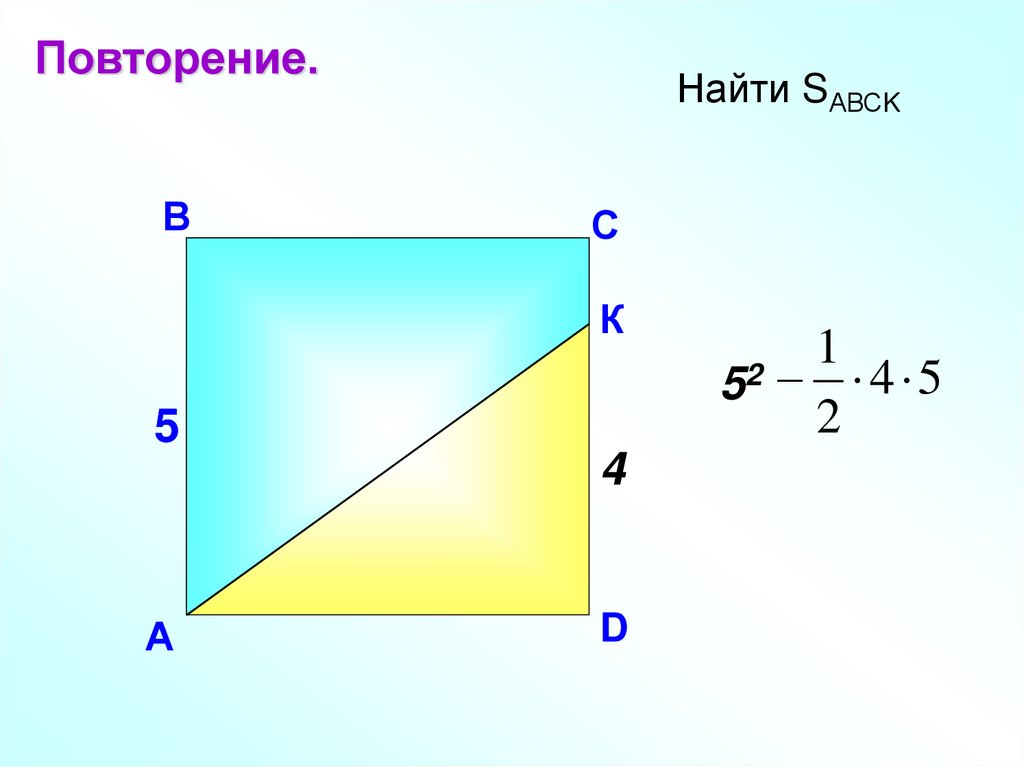
Повторение.Найти SАВС
В
1
S ABC 8 15
2
450
А
8 см
cм
450 0
135
D
7 cм
С
5.
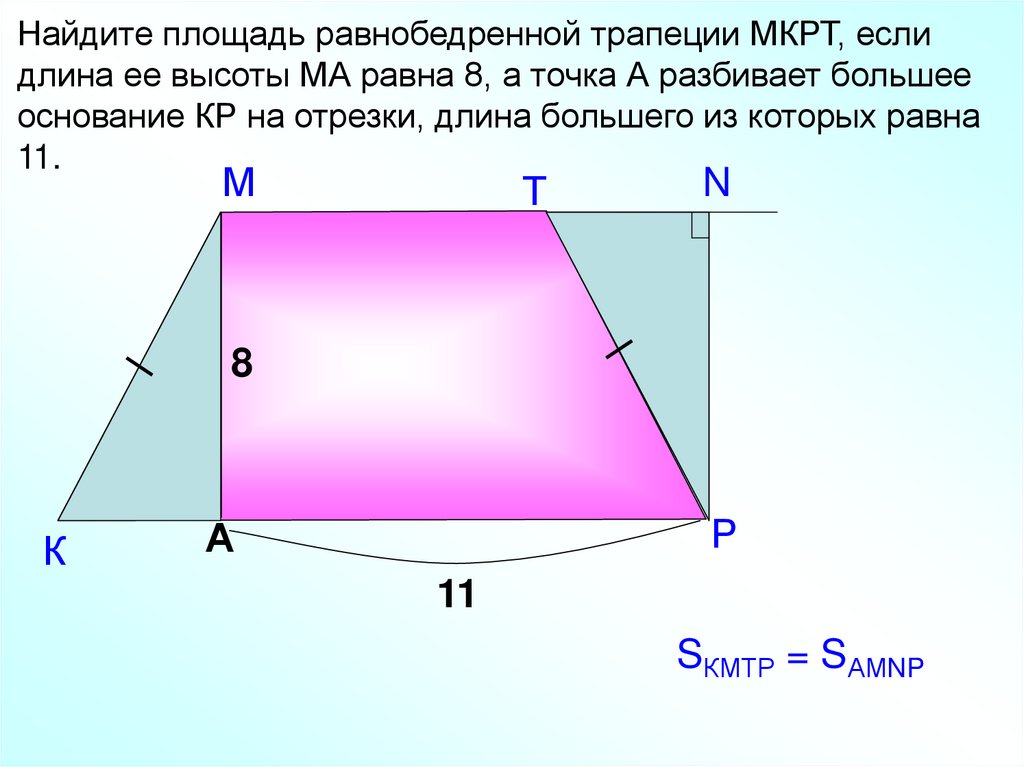
Найдите площадь равнобедренной трапеции МКРТ, еслидлина ее высоты МА равна 8, а точка А разбивает большее
основание КР на отрезки, длина большего из которых равна
11.
М
Т
N
8
К
Р
А
11
SКМТР = SАМNP
6.
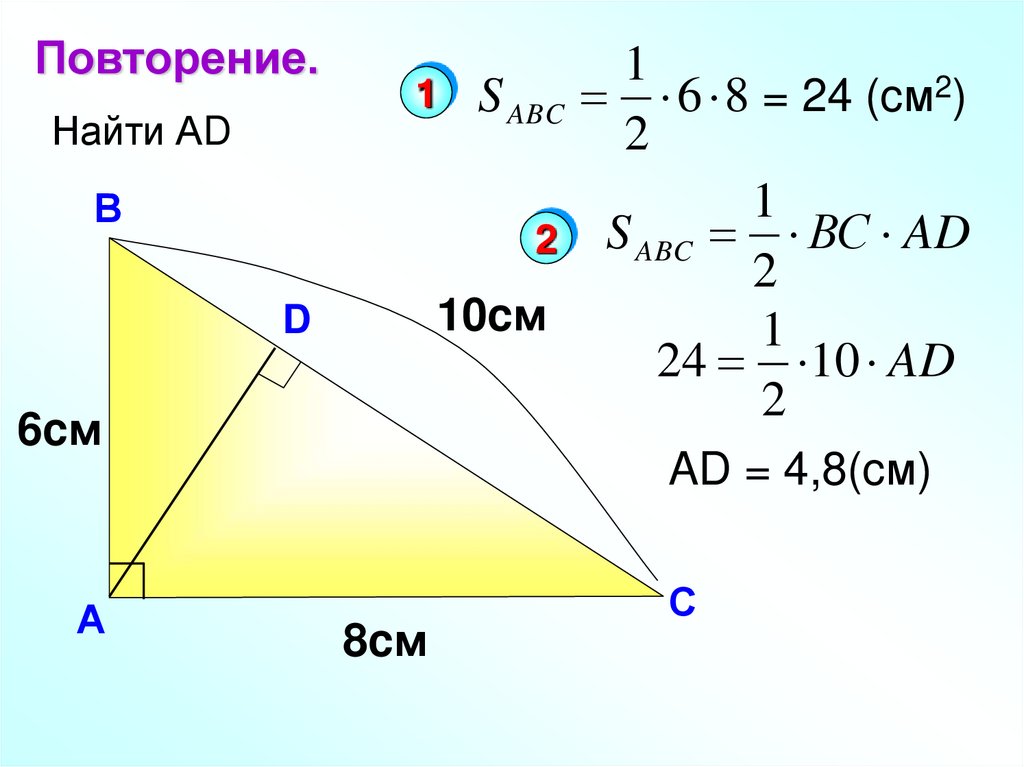
Повторение.Найти АD
В
D
6cм
А
1
1 S ABC 6 8 = 24 (cм2)
2
1
2 S ABC ВС AD
2
10cм
1
24 10 AD
2
AD = 4,8(cм)
8cм
С
7.
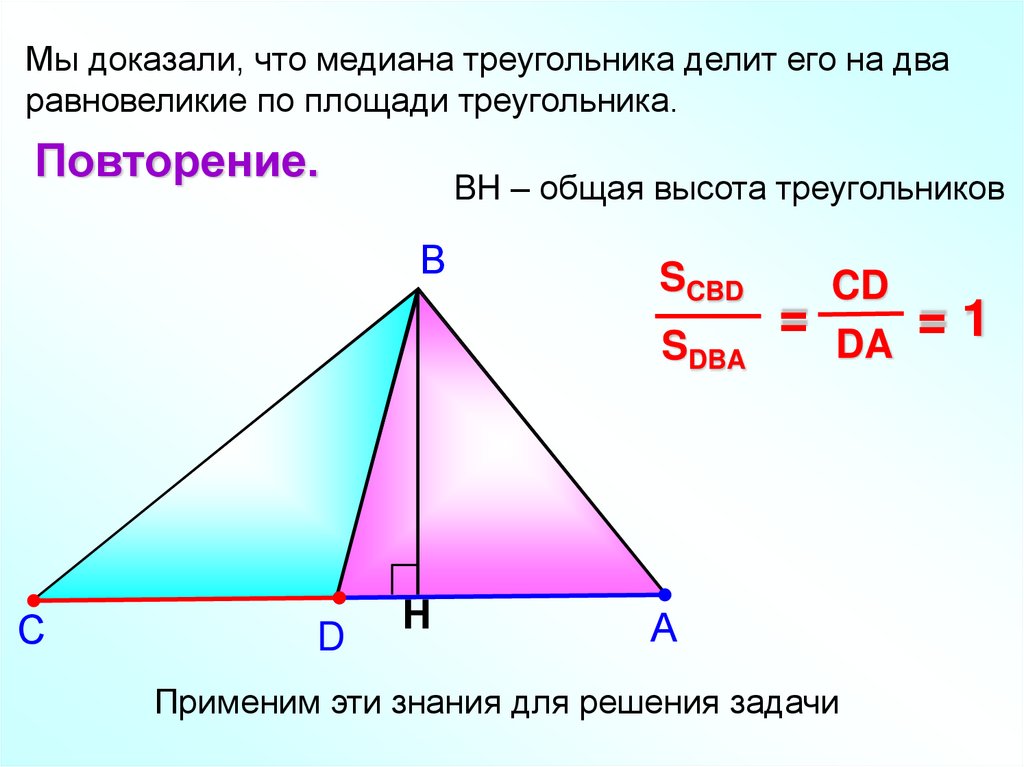
Мы доказали, что медиана треугольника делит его на дваравновеликие по площади треугольника.
Повторение.
BH – общая высота треугольников
В
SCBD
SDBA
С
D
H
CD
= DA = 1
А
Применим эти знания для решения задачи
8.
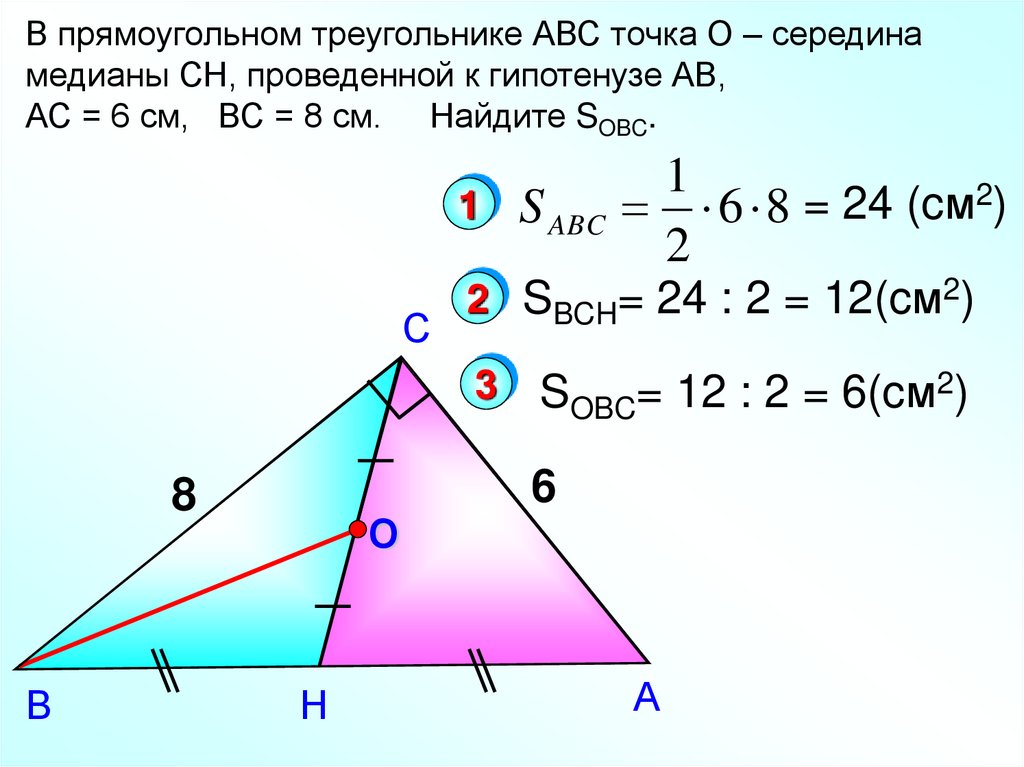
В прямоугольном треугольнике АВС точка О – серединамедианы СН, проведенной к гипотенузе АВ,
АС = 6 см, ВС = 8 см. Найдите SOBC.
1
1 S ABC 6 8 = 24 (cм2)
2
С
2 SBCH= 24 : 2 = 12(cм2)
3
6
8
В
SOBC= 12 : 2 = 6(cм2)
О
Н
А
9.
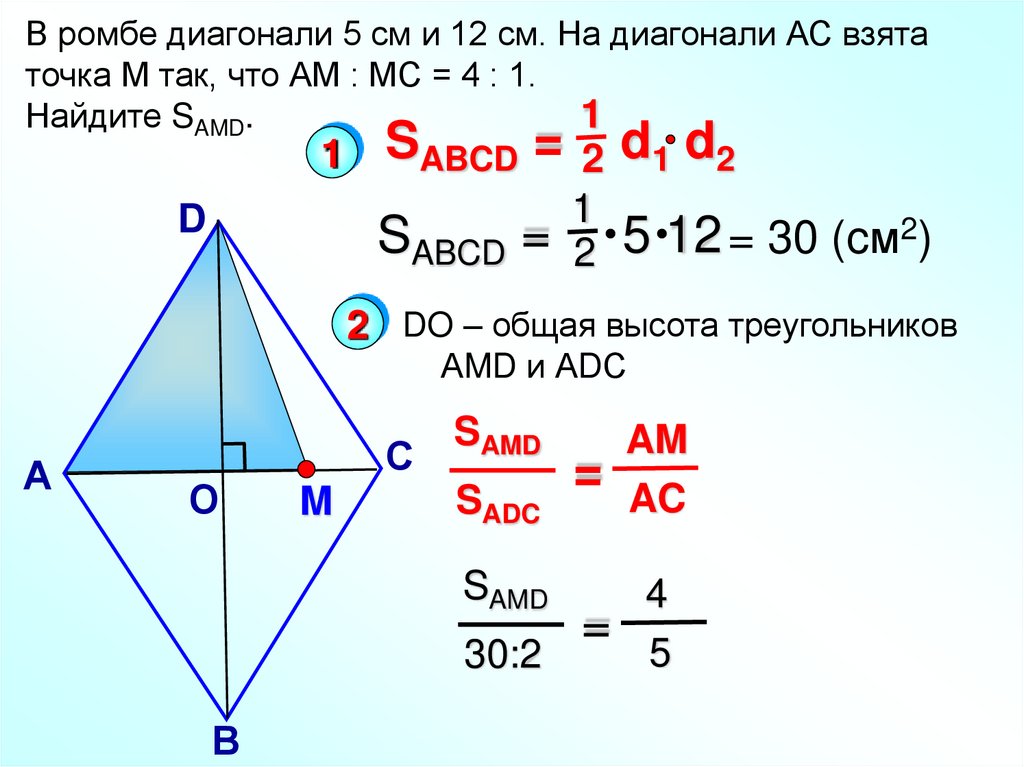
В ромбе диагонали 5 см и 12 см. На диагонали АС взятаточка М так, что АМ : МС = 4 : 1.
Найдите SAMD.
1
1 SABCD = 2 d1 d2
1
SABCD = 2 5 12 = 30 (cм2)
D
2 DO – общая высота треугольников
АMD и АDС
А
О
С
M
SAMD
SADC
SAMD
30:2
В
AM
= AC
=
4
5
10.
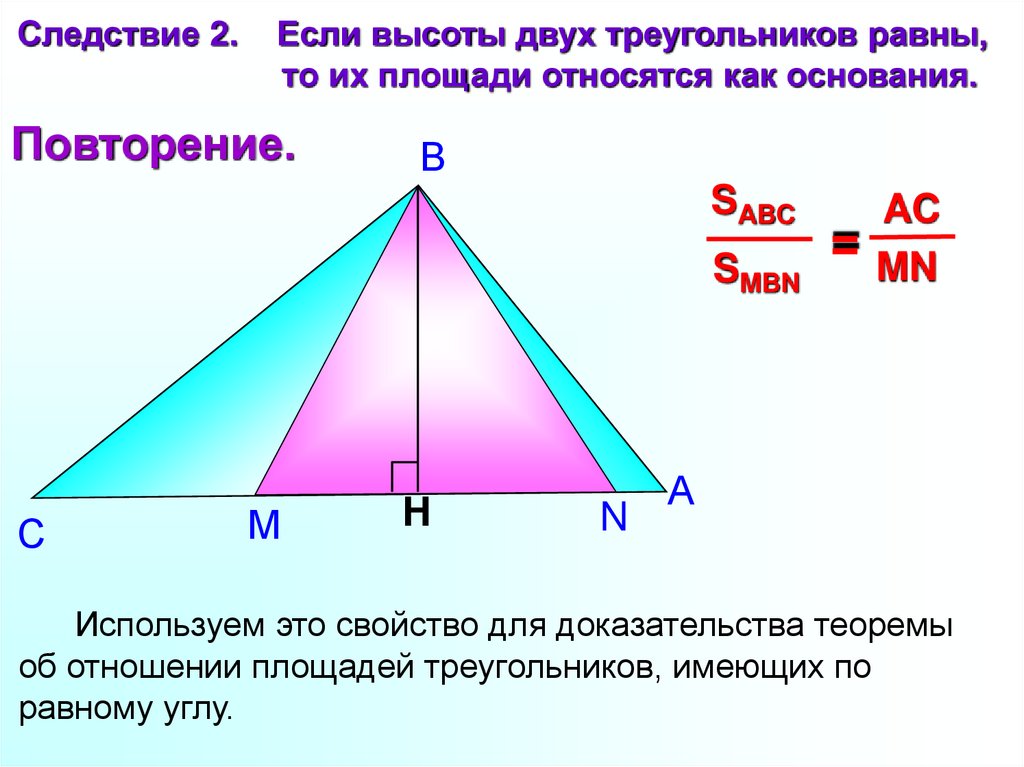
Следствие 2.Если высоты двух треугольников равны,
то их площади относятся как основания.
Повторение.
В
SABC
SMBN
С
М
H
N
AC
= MN
А
Используем это свойство для доказательства теоремы
об отношении площадей треугольников, имеющих по
равному углу.
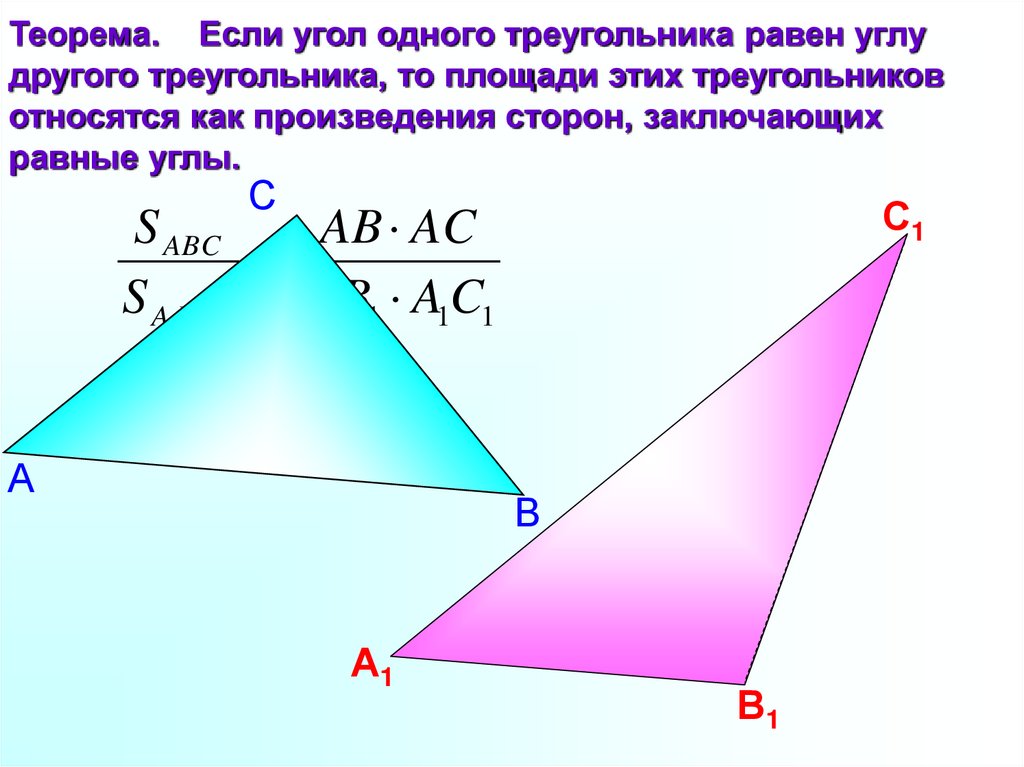
11.
Теорема. Если угол одного треугольника равен углудругого треугольника, то площади этих треугольников
относятся как произведения сторон, заключающих
равные углы.
С
S ABC
AB AC
S A1B1C1 A1 B1 A1C1
А
С1
В
А1
В1
12.
S ABCAB
S AB1C AB1
С
S AB1C
AС
S AB1C1 AС1
АS
СН – общая высота треугольников
АВС и АВ1С
В1Н1 – общая высота
треугольников АВ1С и АВ1С1
С1
АВ AС
S AB1C1 АВ1 AС1
ABC
В
Н1
S ABC
AB AC
S A1B1C1 A1 B1 A1C1
(А1)
Н
В1
13.
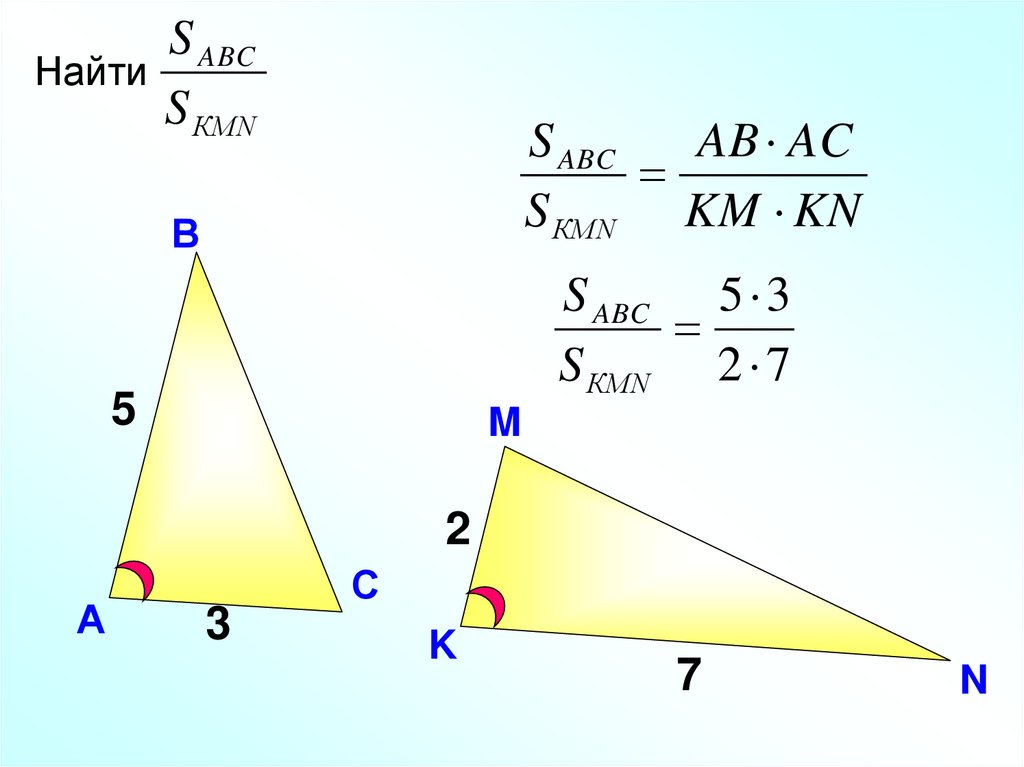
S ABCНайти
S КМN
S ABC
AB AC
S КМN KM KN
В
S ABC 5 3
S КМN 2 7
5
M
2
А
3
С
K
7
N
14.
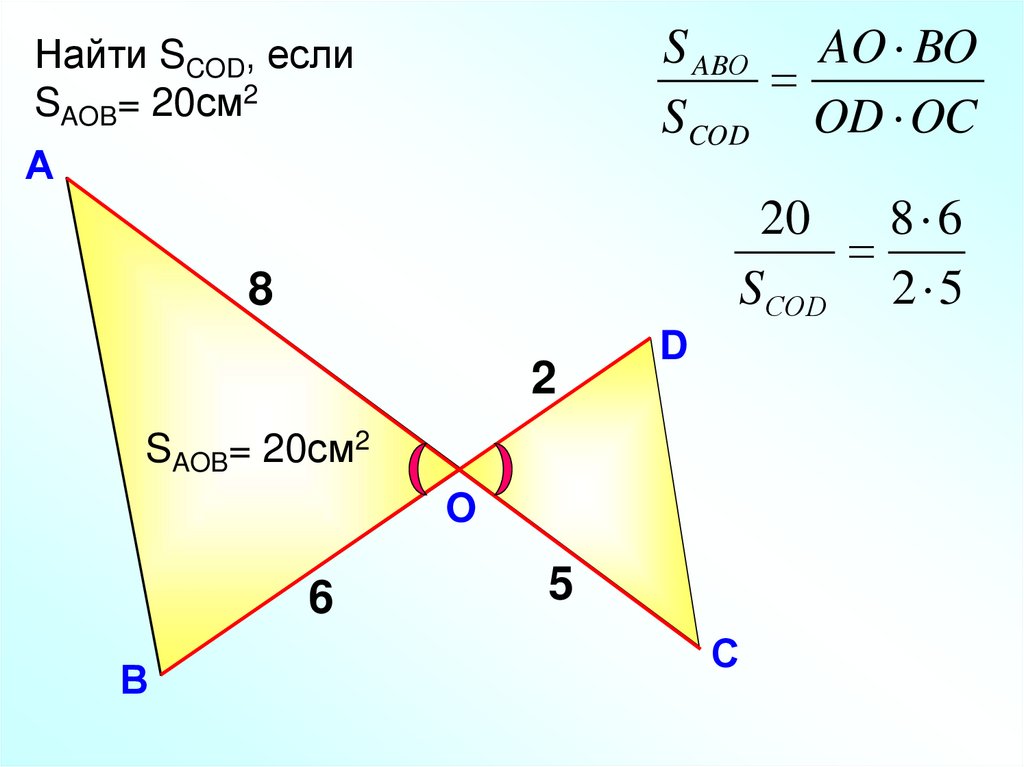
S ABО AO BOS COD OD OC
Найти SCOD, если
SAOB= 20см2
А
20
8 6
S СОD 2 5
8
2
D
SAOB= 20см2
O
6
В
5
С
15.
16.
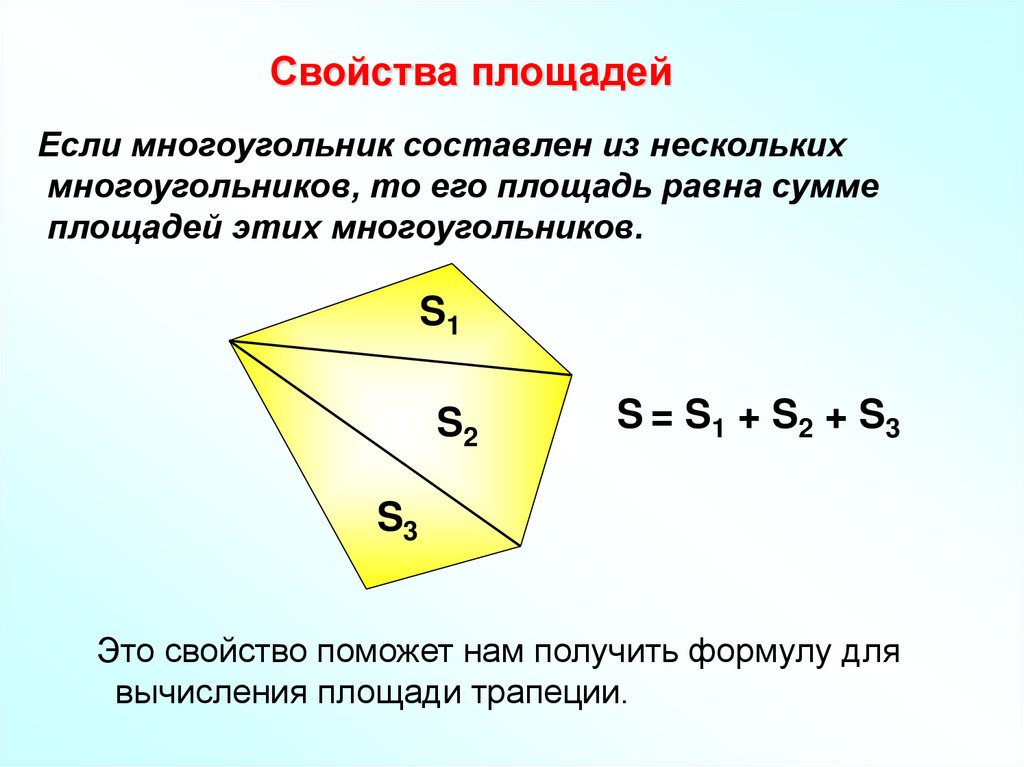
Свойства площадейЕсли многоугольник составлен из нескольких
многоугольников, то его площадь равна сумме
площадей этих многоугольников.
S1
S2
S = S1 + S2 + S3
S3
Это свойство поможет нам получить формулу для
вычисления площади трапеции.
17.
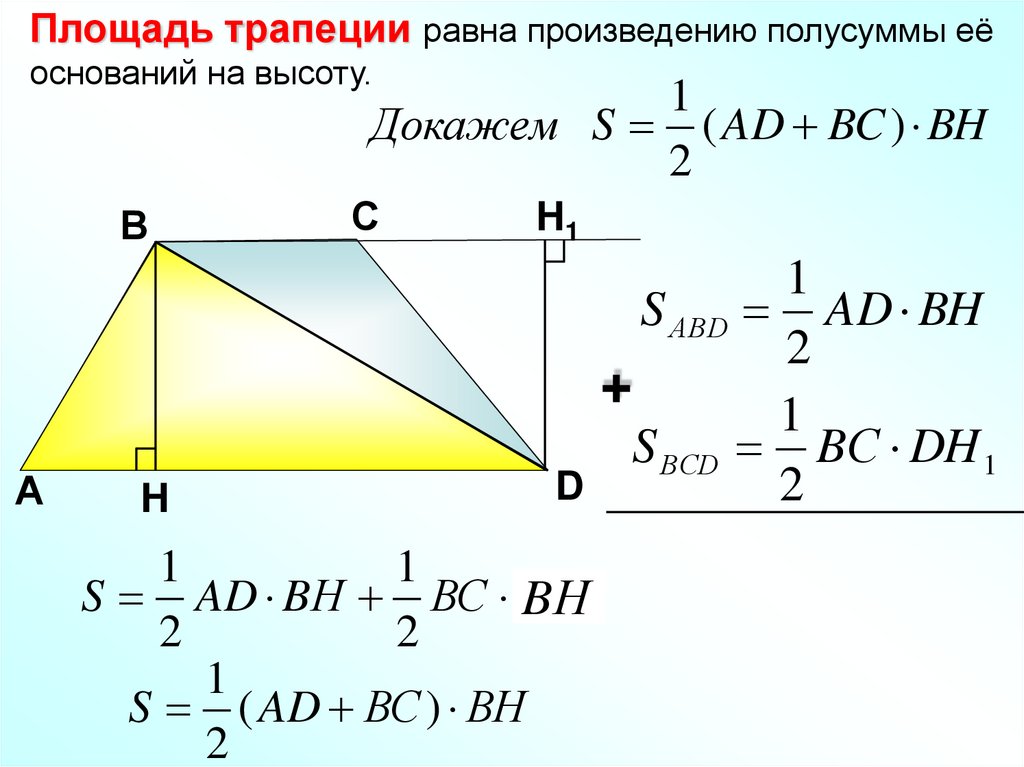
Площадь трапеции равна произведению полусуммы еёоснований на высоту.
1
Докажем S ( AD BC ) BH
2
В
А
H
С
H1
1
S АВD AD BH
2
+
1
S ВСD BС DH 1
D
2
1
1
S AD BН ВС DH
BН1
2
2
1
S ( AD ВС ) ВH
2
18.
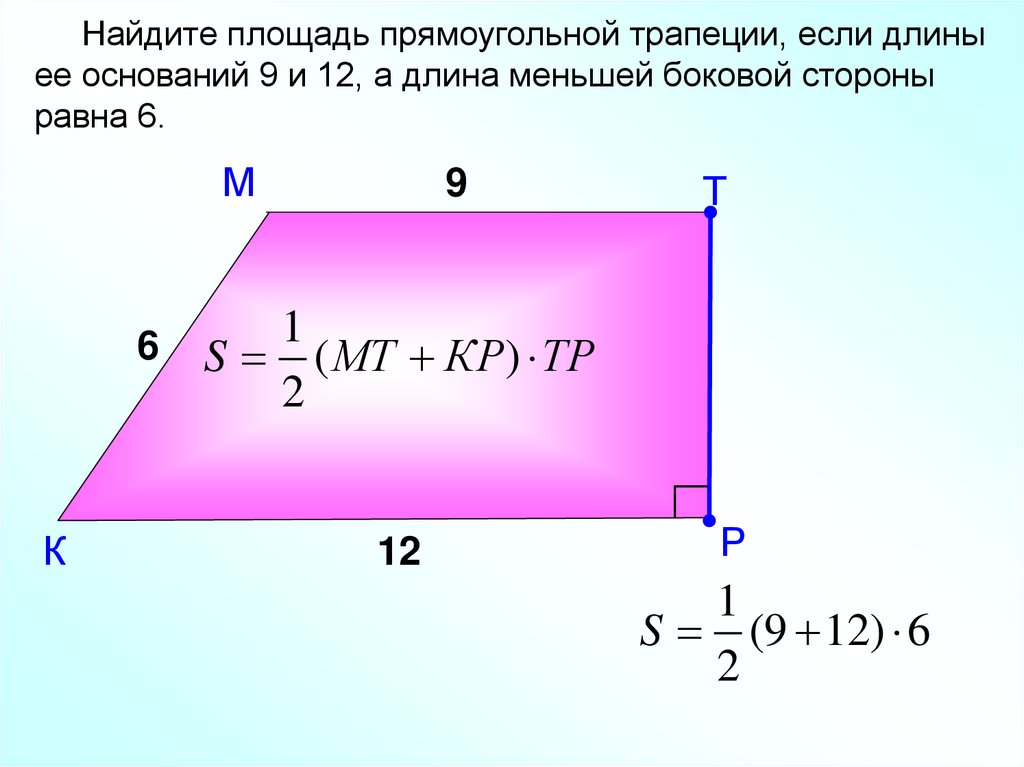
Найдите площадь прямоугольной трапеции, если длиныее оснований 9 и 12, а длина меньшей боковой стороны
равна 6.
М
6
К
9
Т
1
S ( МТ КР) ТР
2
12
Р
1
S (9 12) 6
2
19.
Периметр равнобедренной трапеции равен 32 см, боковаясторона 5 см, площадь 44 см2. Найдите высоту трапеции.
1
М
32 – 5 2 = 22 (см) МТ+КР
1
2 S ( МТ КР) МА
2
Т
1
44 22 МА
2
5
К
А
Р
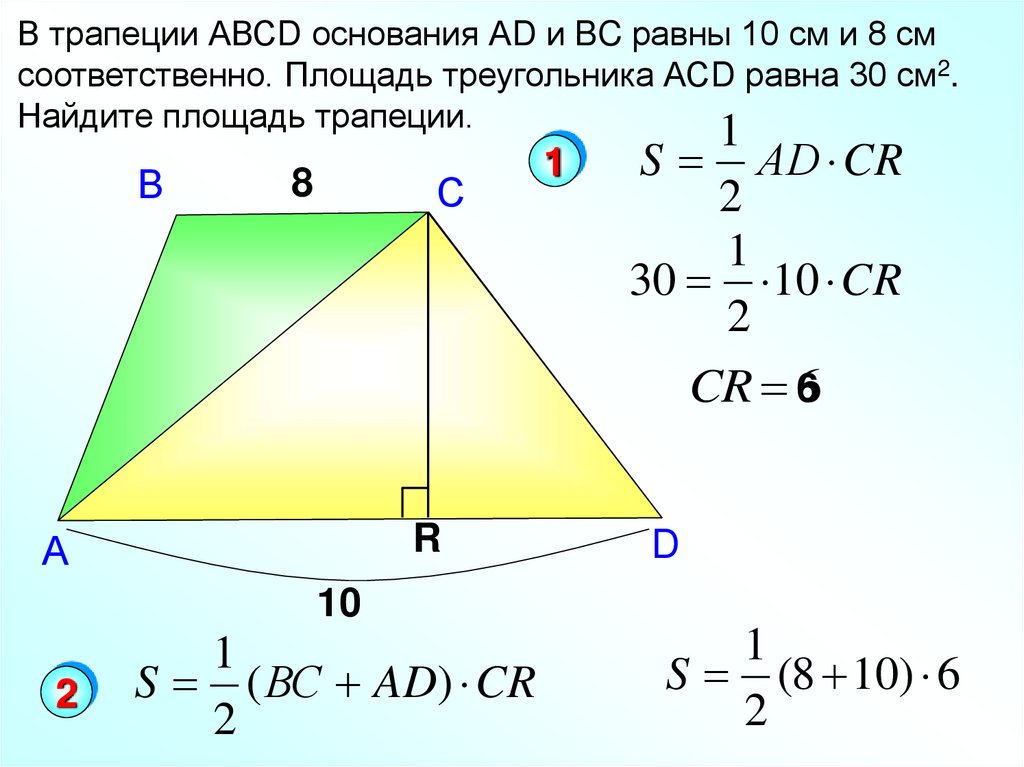
20.
В трапеции АВСD основания АD и BC равны 10 см и 8 смсоответственно. Площадь треугольника АСD равна 30 см2.
Найдите площадь трапеции.
В
8
С
1
1
S АD CR
2
1
30 10 CR
2
CR 6
R
А
D
10
2
1
S ( ВС AD) CR
2
1
S (8 10) 6
2
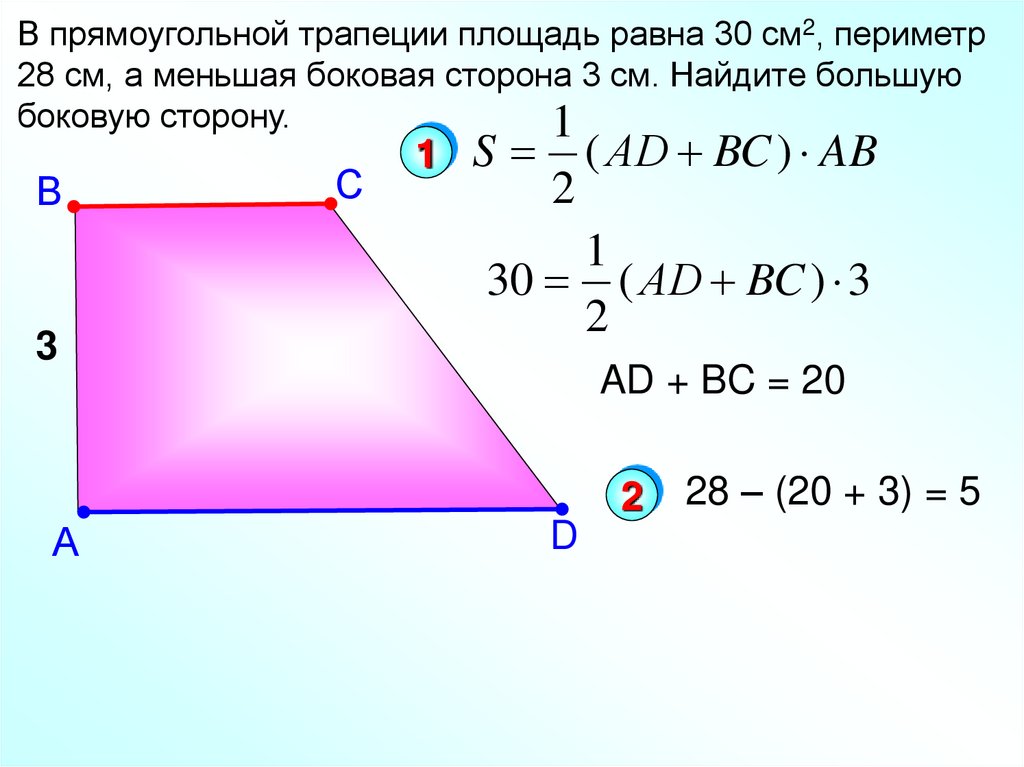
21.
В прямоугольной трапеции площадь равна 30 см2, периметр28 см, а меньшая боковая сторона 3 см. Найдите большую
боковую сторону.
1
В
3
С
1 S
2
( АD BC ) AB
1
30 ( АD BC ) 3
2
AD + BC = 20
2
А
D
28 – (20 + 3) = 5
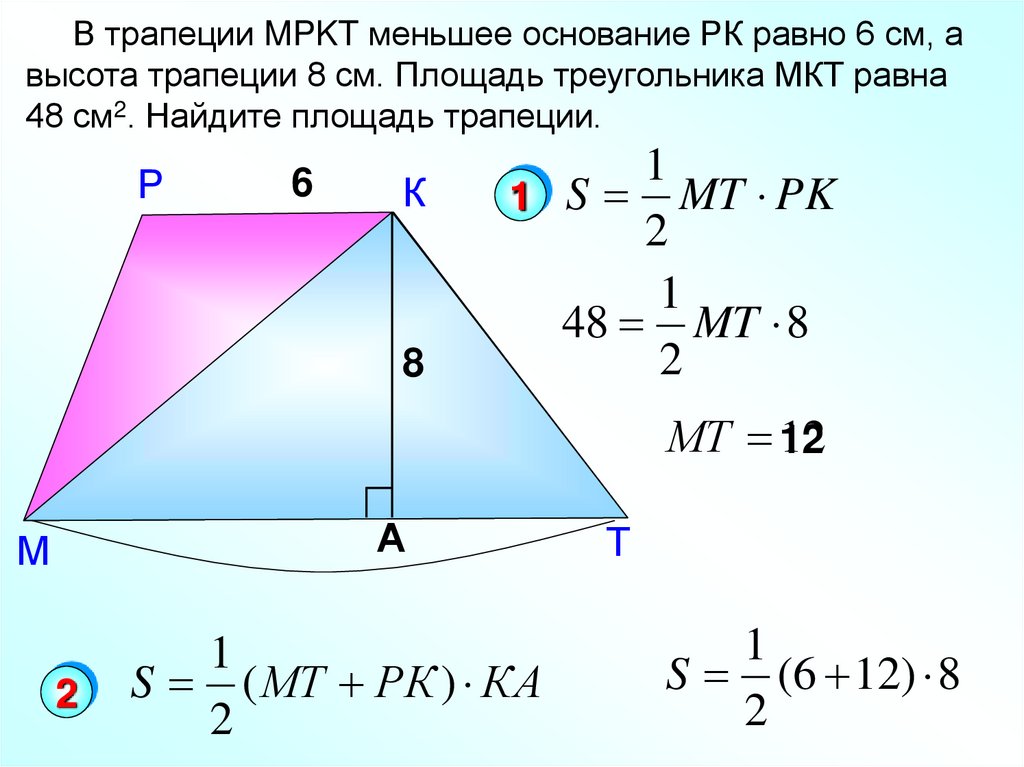
22.
В трапеции MPKT меньшее основание РК равно 6 см, авысота трапеции 8 см. Площадь треугольника МКТ равна
48 см2. Найдите площадь трапеции.
Р
6
К
8
1
1 S MT PK
2
1
48 MT 8
2
МТ 12
А
М
2
1
S ( МТ РК ) КА
2
Т
1
S (6 12) 8
2
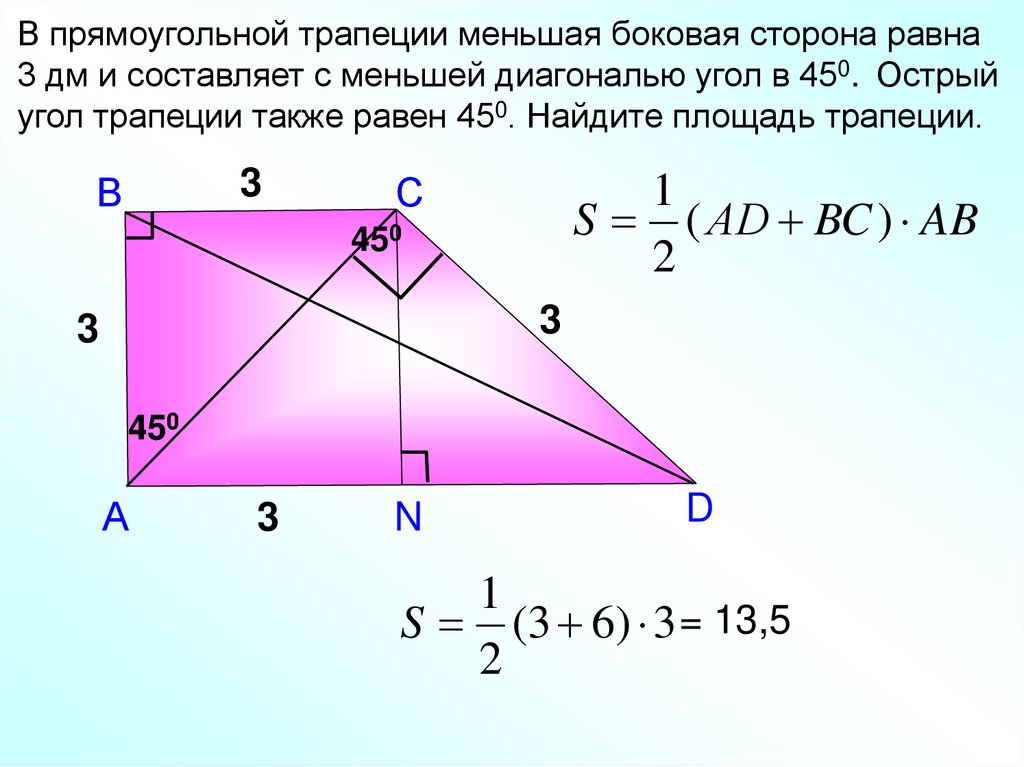
23.
В прямоугольной трапеции меньшая боковая сторона равна3 дм и составляет с меньшей диагональю угол в 450. Острый
угол трапеции также равен 450. Найдите площадь трапеции.
3
В
С
1
S ( АD BC ) AB
2
450
3
3
450
А
3
N
D
1
S (3 6) 3 = 13,5
2




 mathematics
mathematics