Площадь треугольника (8 класс)

1.

8 класс

2. Устная работа.

В
А
30
С
0
К 9 см
D
ABCD – параллелограмм.
Найти площадь параллелограмма.

3. Устная работа.

В
60
А
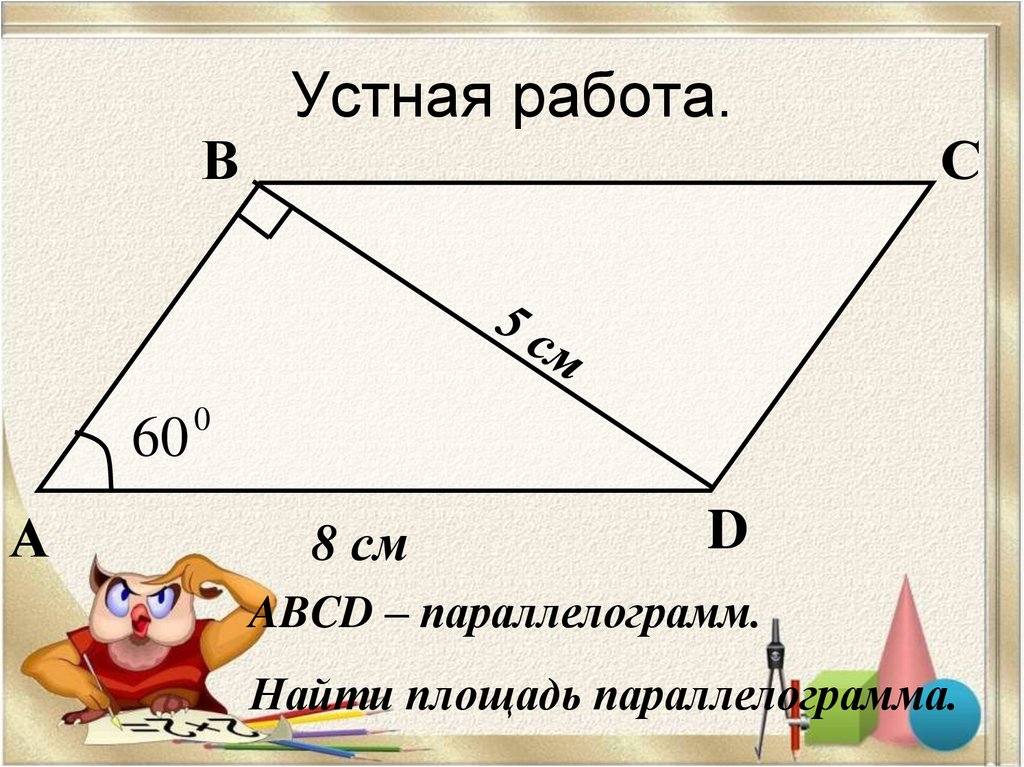
Устная работа.
С
0
8 см
D
ABCD – параллелограмм.
Найти площадь параллелограмма.

4.

Дано:
Параллелограмм ABCD
AB – 8см
AD – 10см
угол А – 30 градусов
Найти: Площадь ABCD
8
30
Н
10
Решение:
S = BH*AD
S = (8:2)*10
S = 40 cм2
Ответ: 40 см2

5.

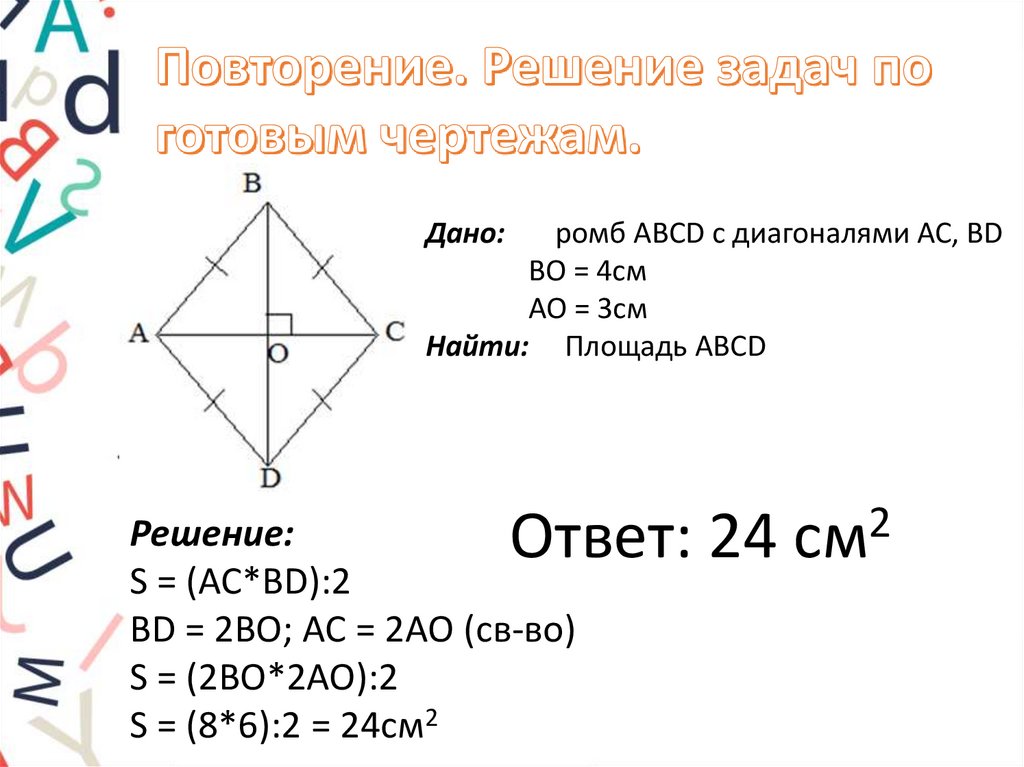
Дано:
ромб ABCD с диагоналями AC, BD
BO = 4см
AO = 3см
Найти: Площадь ABCD
Ответ: 24 см2
Решение:
S = (AC*BD):2
BD = 2BO; AC = 2AO (св-во)
S = (2BO*2AO):2
S = (8*6):2 = 24см2

6.

Дано:
H Н
Параллелограмм ABCD
BH – высота
BH = 2 см
HD = 3 см
угол BAH = 45 градусов
Найти:
Площадь ABCD
Решение:
S = BH*AD
Треуг-ник AHB – р\б, значит
AH=BH=2см
AD = AH+HD = 2см+3см=5см
S = 5см*2см=10см2
Ответ: 10см2

7.

В
Н1
К
А
Н
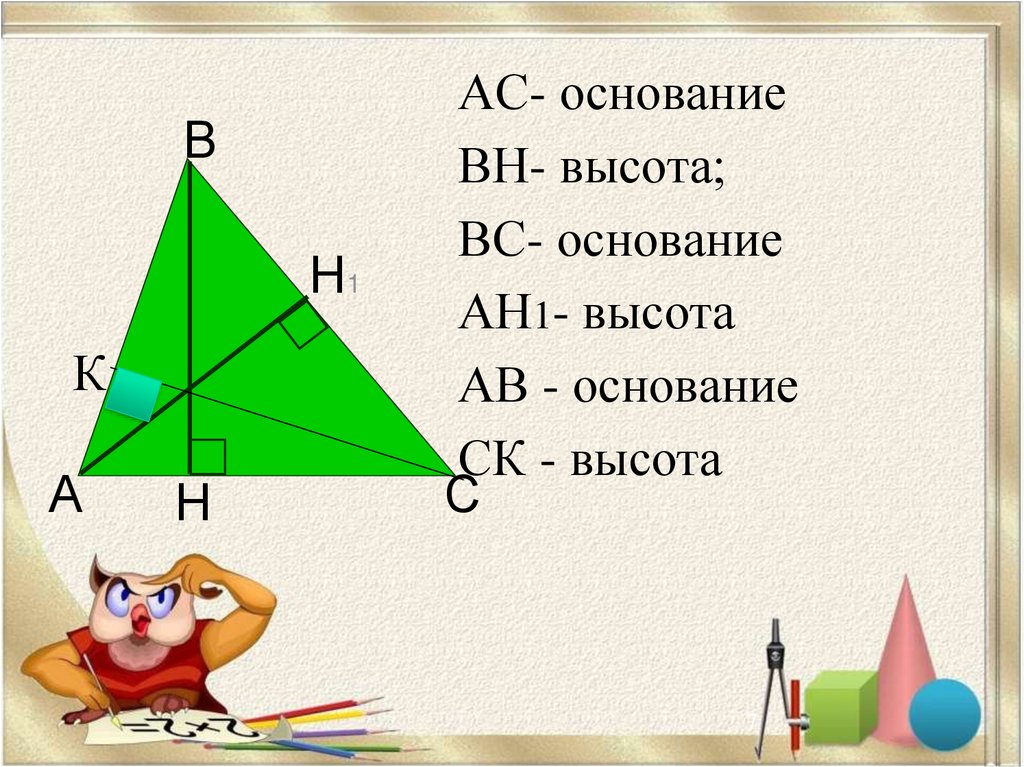
АС- основание
ВН- высота;
ВС- основание
АН1- высота
АВ - основание
СК - высота
С
7

8.

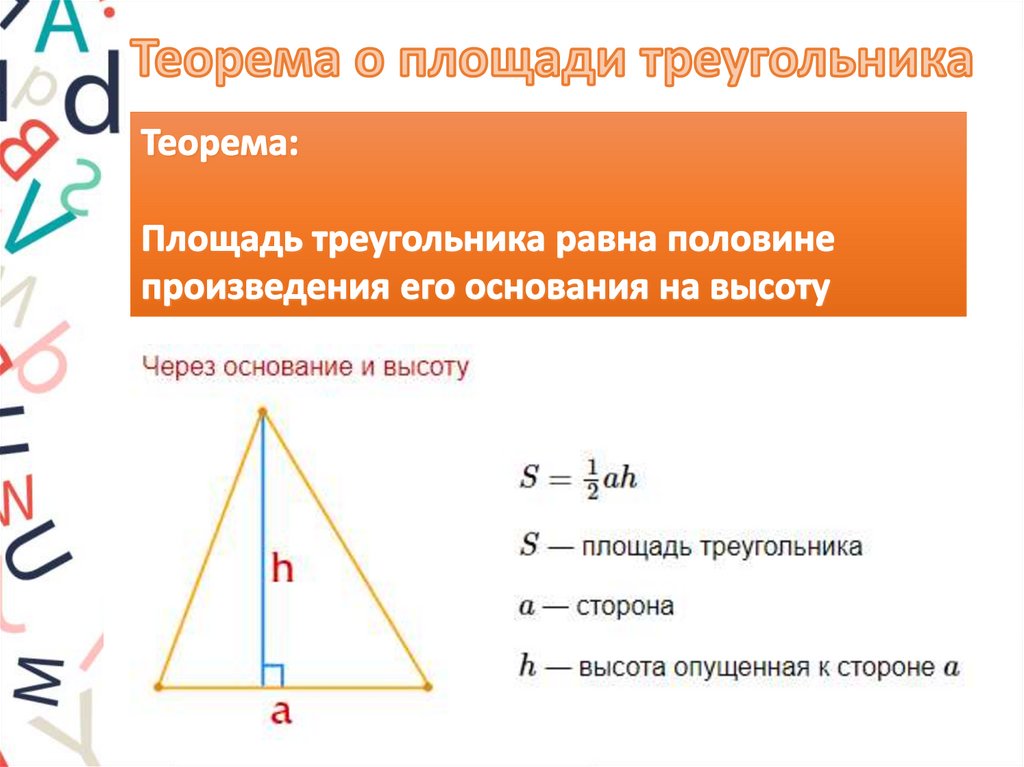
9. Теорема. Площадь треугольника равна половине произведения его основания на высоту.

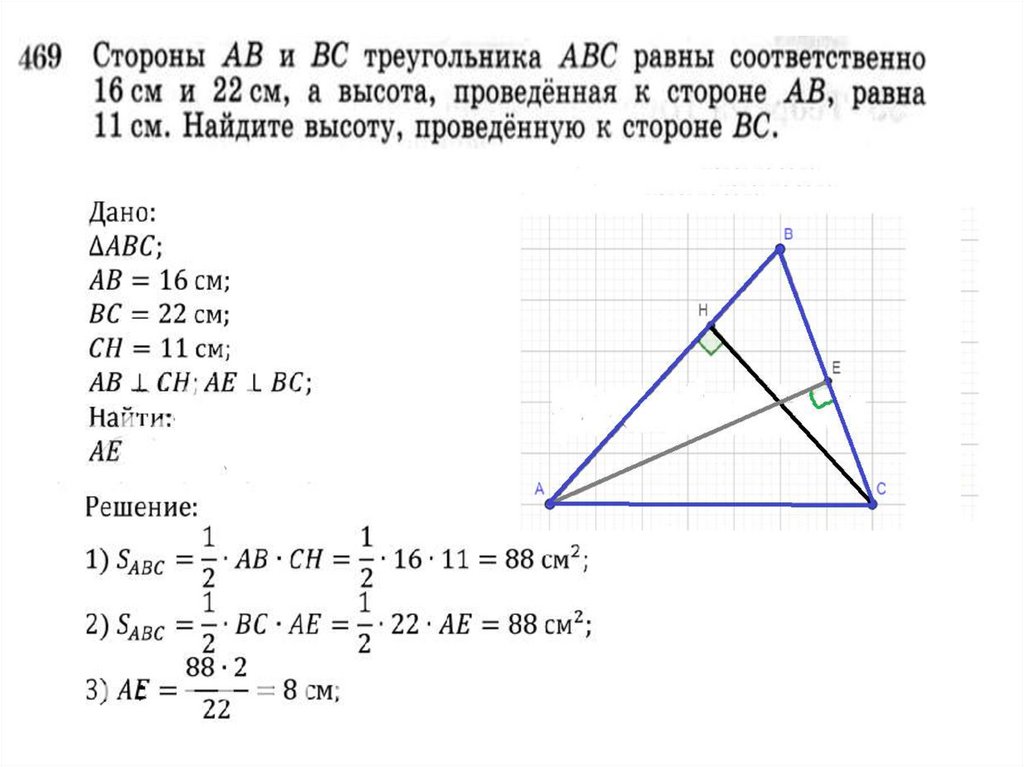
С
А
Н
D
В
Дано: АВС;
СН- высота;
АВ- основание.
Док-ть: S= ½ АВ* СН.
Док-во: АВС= DСВ (по трем сторонам
(СВ- общая, АВ= СД, АС= ВД ))
SАВС =SDСВ
SАВС= ½ SАBCD, т.е. S = = ½ АВ СН.
Теорема доказана.
9

10.

11.

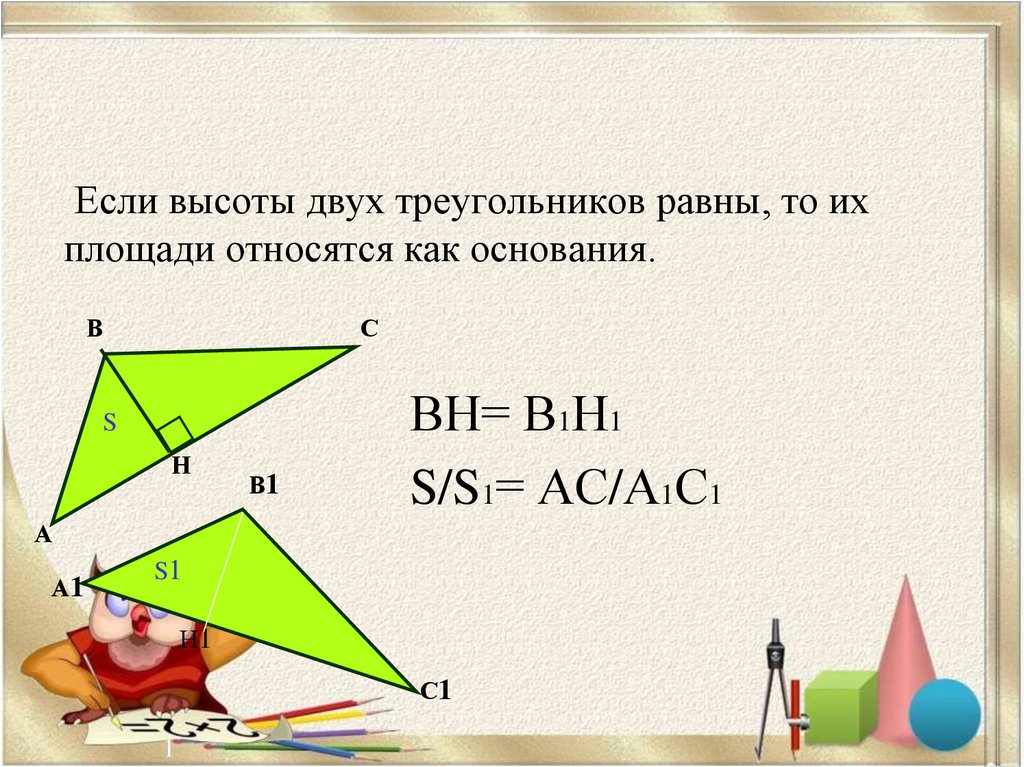
Если высоты двух треугольников равны, то их
площади относятся как основания.
В
С
S
Н
В1
ВН= В1Н1
S/S1= АС/А1С1
А
А1
S1
Н1
С1
1

12.

13.

14. №468(б,г)

15.

16.

17.

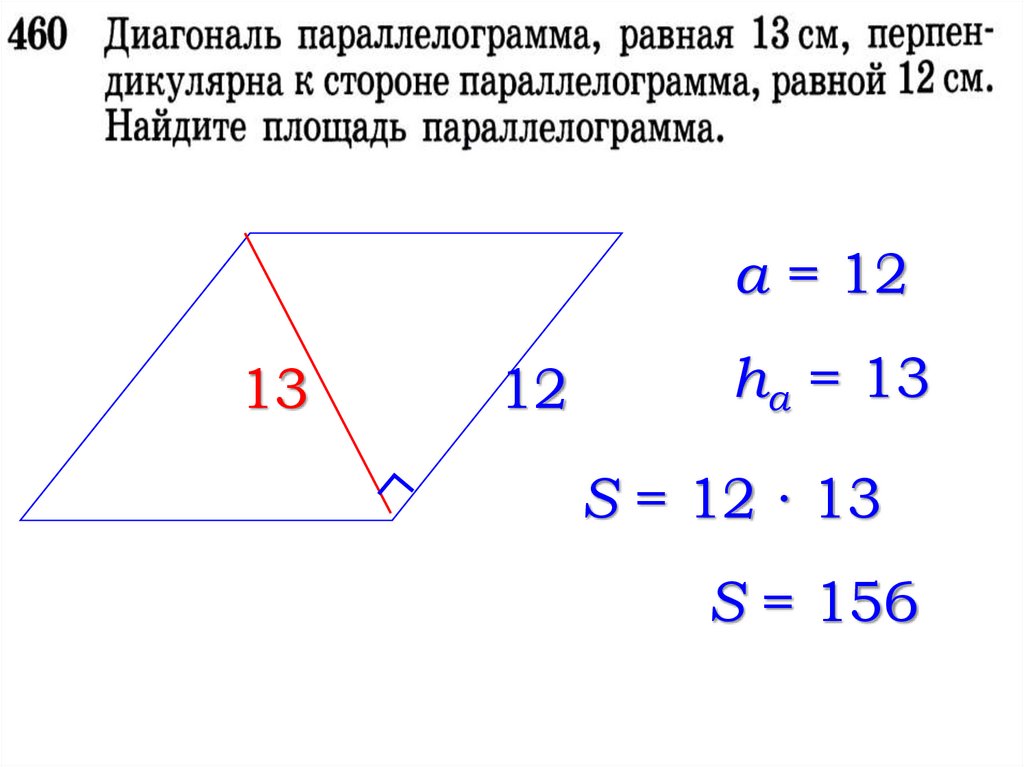
a = 12
13
12
ha = 13
S = 12 ∙ 13
S = 156

18.

S = a ∙ ha
6
x-?
∟
1
5
a = 10,ha = 6
10
S = 10 ∙ 6=60
a =15, ha = х
х = 60 : 15 = 4

19.

12
B
8
∟
0
30
A
Н
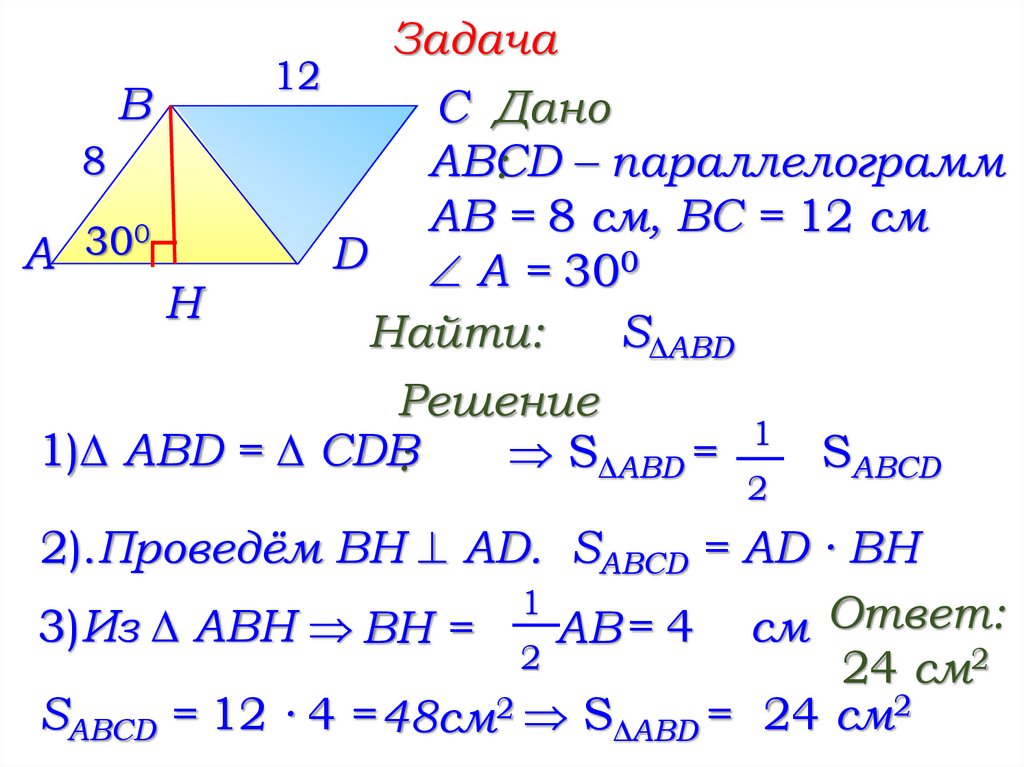
Задача
C Дано
ABCD
: – параллелограмм
AB = 8 см, BC = 12 см
D A = 300
Найти:
S∆ABD
Решение
1)∆ ABD = ∆ CDB:
S∆ABD =
1
2
SABCD
2).Проведём ВН AD. SABCD = AD ∙ BH
1
3)Из ∆ АВН ВН =
АВ = 4 см Ответ:
2
24 см2
SABCD = 12 ∙ 4 = 48см2 S∆ABD = 24 см2