Similar presentations:
Тетеорема Штейнера
1. ТЕОРЕМА ШТЕЙНЕРА
• Позволяет найти момент инерцииотносительно оси, которая параллельна
оси, проходящей через центр масс
А
С
a
JC
JA
J A J C Ma
2
2. Момент инерции тонкого кольца относительно оси, проходящей через точку на ободе, перпендикулярно ему
J A J C MaJC
R
С
JA
А
J C MR2
2
a R
J A MR MR 2MR
2
2
2
3. Момент инерции тонкого стержня относительно оси, проходящей через край стержня, перпендикулярно ему
JCJA
С
L
2
ML
JA
3
А
J A J C Ma
2
2
L
a
2
12
2
2
2
ML
ML ML
JA
3
4
12
J C ML
4. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ
• Разобьем вращающееся тело на маленькиеобъемы mi, находящиеся на расстоянии ri от оси
вращения
r1
r2
r3
m1
m2
m3
5.
• Центры окружностей лежат на оси вращения(по определению)
• Угловая скорость вращения этих объемов
одинакова, а линейная - различна
V1 V2
r1
r2
6.
• Кинетическая энергия вращающегося тела2
1 1
2
2 2
mV
mV
Tвр
2
2
Vi ri
mi ri 2 2
Tвр
2
2
i
2
i
miVi
i 2
J
mi ri
2
2
J – момент инерции тела
2
2
Tв р
7.
• В случае плоского движения твердоготела кинетическая энергия складывается
из кинетической энергии поступательного
движения и кинетической энергии
вращательного движения
mV
J C
T
2
2
2
C
2
VC- скорость поступательного
движения центра масс
JC- Момент инерции тела относительно оси,
проходящей через центр масс
8. ПРИМЕР
• Найдем кинетическую энергиюкатящегося сплошного цилиндра (m)
R
VC
9.
mVJ C
T
2
2
2
C
2
mR 2
JC
2
VC
R
2
C
mV
1 mR
T
2
2 2
2
C
2
C
mV
mV
2
4
2
2
VC
2
R
2
C
3mV
4
10. Момент импульса
• Моментом импульсаматериальной точки
относительно точки
О называется
векторное
произведение
m
О
r
L [ r P]
r
P mV
α
V
L
L r P sin
11. Момент импульса относительно неподвижной оси Z
• - скалярная величина, равная проекциина ось момента импульса,
определенного относительно
произвольной точки О , лежащей на оси
L
LZ
O
Z
12. Момент импульса системы материальных точек
• Моментом импульсасистемы
материальных точек
называется
векторная сумма
моментов импульса
всех материальных
точек системы
N
L [ri Pi ]
i 1
13.
• Рассмотрим движение материальнойточки по окружности
r
V
L
L r P sin
P
m
V
2
L r mV
Проекция момента импульса на ось Z
LZ mVr
14. Момент импульса твердого тела относительно оси вращения
LZi miVi riLZ miVi ri
i
LZ
Vi ri
m
r
i i J Z LZ
2
i
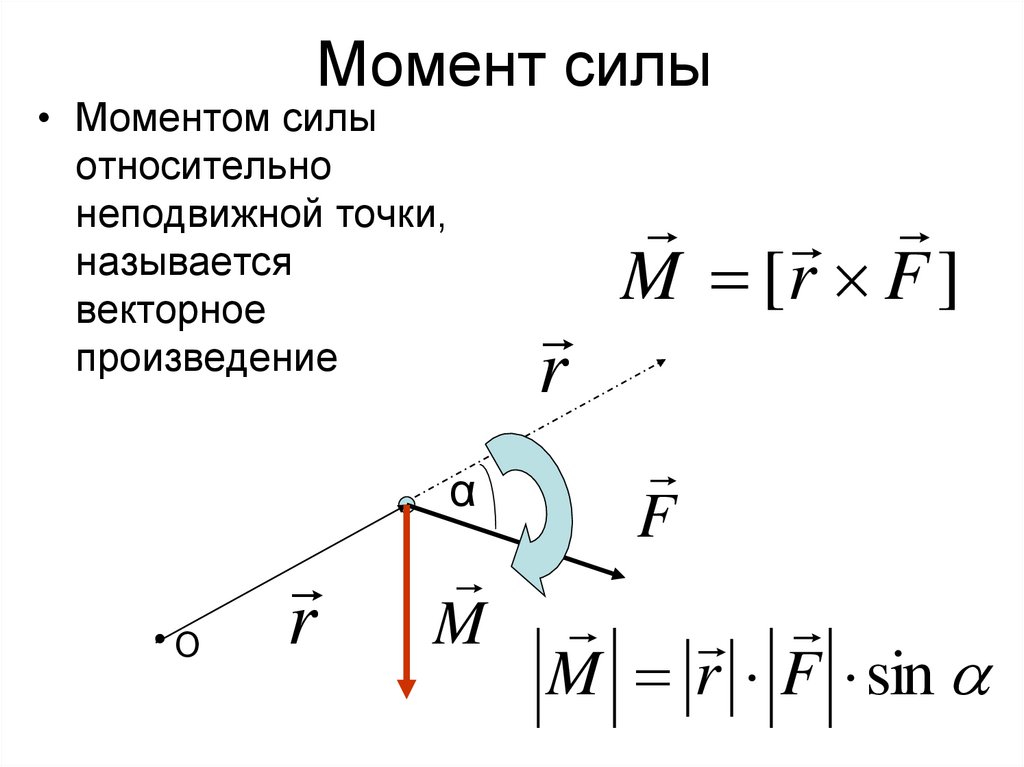
15. Момент силы
• Моментом силыотносительно
неподвижной точки,
называется
векторное
произведение
r
α
О
r
M
M [r F ]
F
M r F sin
16. Момент силы относительно неподвижной оси Z
• - скалярная величина, равная проекциина ось момента силы, определенного
относительно произвольной точки О ,
лежащей на оси
M
MZ
O
Z
17. Закон сохранения момента импульса
L [ r P]d
dr
dP
L [ P ] [r ]
dt
dt
dt
dL
[V P ] [ r F ]
dt
d
L
[V P] 0 [r F ] M
M
dt
18.
• В замкнутой системеdL
0
dt
M 0
L const
• В замкнутой системе момент импульса
сохраняется
19.
20.
21.
22.
23.
• https://www.youtube.com/watch?v=SkE4NWOnWhk кошки
• https://www.youtube.com/watch?v=UZlW1
a63KZs – момент импульса
24.
• http://www.youtube.com/watch?v=RtWbpyjJqrU (ПОЧЕМУ КОШКИ ПАДАЮТ НА 4
ЛАПЫ)
25.
J1J2
J1
J2
J1 1 ( J1 J 2 )
1 J1
J1 J 2
26. Основное уравнение динамики вращательного движения тела с закрепленной осью
LZ J ZdLZ
d
JZ
J Z
dt
dt
M z J Z
dLZ
MZ
dt
-Основное уравнение динамики
вращательного движения
27. пример
• Через блок, имеющий форму диска,перекинута нерастяжимая нить, на
которой подвешены два груза. Масса
диска m, массы грузов m1 > m2. С каким
ускорением будут двигаться грузы ?
28.
T2/aT
2
m2
m2g
m
m1>m2
T1/
T1
m1
m1g
a
29. Для 1 грузика 2 закон Ньютона
m1a m1g T1В проекциях
m1a m1g T1
30. Для 2 грузика 2 закон Ньютона
m2a m2 g T2В проекциях
m2a m2 g T2
m2a m2 g T2
31. Для блока основное уравнение динамики вращательного движения
M JmR
J
2
M
2
Момент инерции блока
Угловое ускорение
Результирующий момент
сил, действующих на блок
32.
T2m
r
T1
M2
m2
M 2 T2 R
m1
M1
M1 T1 R
33.
• На блок действуют силы T1/ иT2/M T1 R T2 R
• Нити не растягиваются, поэтому
T1 T1
T2 T2
M T1 T2 R
34.
• Линейное и угловое ускорение связанымежду собой
a
R
• Основное уравнение динамики
вращательного движения для блока
a mR 2 a
M T1 T2 R J J
R
2 R
T1 T2 R mRa
2
35.
maT1 T2
2
m1a m1g T1
m2a m2 g T2
T1 m1 g a
T2 m2 a g
36.
mam1 g a m2 a g
2
ma
m1g m1a m2a m2 g
2
ma
g m1 m2
a m1 m2
2
37.
g m1 m2a
m
m1 m2
2
38. Работа внешних сил при вращении твердого тела вокруг неподвижной оси
2J Z
dA dTв р
Tв р
2
2
2
J
dTв р d ( Z ) J Z d ( ) 2 J d
2
2
2
dA J Z d
39.
dM z JZ
dt
M z J Z
M z dt J Z d
dA J Z d M z dt
d
dt
d dt
dA M Z d
A M Z d








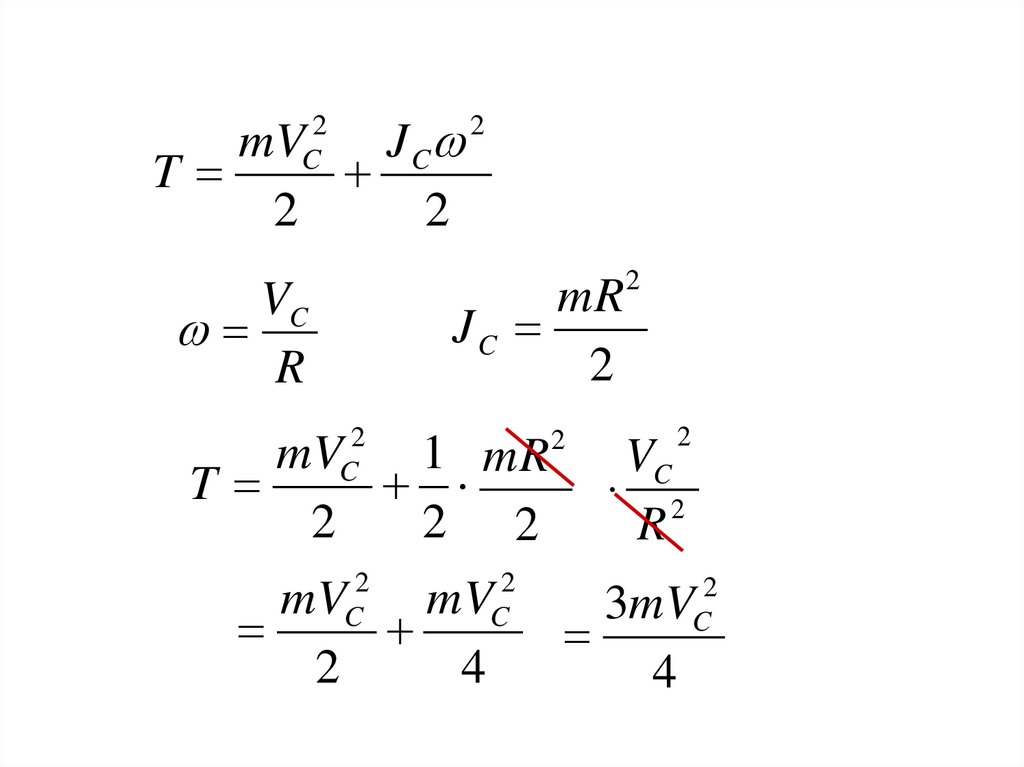





























 physics
physics








