Физика. Механика

1. Физика МЕХАНИКА

Храмов Владимир Николаевич
Физика
МЕХАНИКА
Мультимедийные лекции
кафедры
лазерной
физики

2. Общая физика

Механика
Молекулярная физика
Электричество и магнетизм
Оптика
Физика атомов и атомных явлений
Физика атомного ядра и частиц

3. Структура дисциплины «Механика»

1.
Введение. Механика – раздел курса общей
физики
2. Кинематика материальной точки
3. Динамика материальной точки
4. Система материальных точек
5. Законы сохранения в механике
6. Неинерциальные системы отсчета
7. Кинематика абсолютно твердого тела
8. Динамика абсолютно твердого тела
9. Движение тела с переменной массой
10. Столкновения
11. Колебательное движение
12. Основы специальной теории относительности

4. ОСНОВНАЯ ЛИТЕРАТУРА

УЧЕБНИКИ
Сивухин Д.В. Общий курс физики. В 5 томах. Т. 1. Механика
Матвеев А.Н. Механика и теория относительности
Стрелков С.П. Механика
ЗАДАЧНИКИ
Стрелков С.П., Сивухин Д.В., Угаров В.А., Яковлев И.А.
Сборник задач по общему курсу физики. Механика / Под
ред. И.А. Яковлева. 4-е изд. М. : Наука, 1977. 288 с.
Иродов И.Е. Задачи по общей физике: Учебное пособие. 2-е
изд. М. : Наука, 1988. 416 с.

5. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

• Белянкин А. Г., Матвеев А. Н., Сараева И. М., Устинова А. В., Шушурин
С. Ф. Методика решения задач механики: Метод. пособие / Под
ред. А. Н. Матвеева. М.: Изд-во МГУ, 1980. 160 с.
• Иродов И.Е. Основные законы механики: Учеб. Пособие для физ.
спец. вузов. 3-е изд., перераб. и доп. М. : Высш. шк., 1985. 248 с.
• Савельев И.В. Курс общей физики. В 4-х томах. Том 1. Механика.
Молекулярная физика и термодинамика
• Киттелль Ч. , Найт У., Рудерман М. Берклеевский курс физики. Т.1.
Механика
• Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по
физике. Том. 1. Современная наука о природе. Законы
механики. Том 2. Пространство, время, движение

6.

1. Введение. Механика раздел курса общей
физики
1.1. Физические величины
1.2. Системы физических величин
1.3. Размерности физических величин

7. Задачи и методы физики

Задача физики состоит в создании в
нашем сознании такой модельной картины
физического мира, которая наиболее полно
отражает его свойства.
Физика – наука экспериментальная.
Экспериментальный метод физики состоит в
следующем: на основе экспериментов и
наблюдений создается модель, в рамках
которой делаются предсказания о явлениях,
проверяемых
в
свою
очередь
в
экспериментах и наблюдениях. В результате
этого уточняется модель, и делаются новые
предсказания.

8. Физические величины и их измерение

Свойства и качества, которыми оперирует физика,
называются физическими величинами.
Измерением
физических
свойств
называется
процедура соотнесения этим свойствам некоторых
чисел таким образом, чтобы сравнение свойств
можно было провести путем сравнения чисел.

9. Основные величины и единицы измерения Международной системы единиц (СИ)

Длина (размерность – L) – величина, характеризующая протяженность,
удаленность и перемещение тел или их частей вдоль заданной линии.
Единица длины – метр (м). Метр – это длина пути, проходимого в вакууме
светом за 1/299 792 458 долю секунды. Это определение было принято в
октябре 1983 г.
Масса (размерность – M) – величина, определяющая инертные и
гравитационные свойства материальных объектов.
Единица массы – килограмм (кг). Килограмм равен массе международного
прототипа килограмма.
Новое определение килограмма:
1 килограмм равен постоянной Планка, поделенной на 6,626070040 ×
10−34 м2·с−1. Для выражения единицы требуется постоянная Планка.

10. Основные величины и единицы измерения Международной системы единиц (СИ)

Время – величина, характеризующая последовательную смену явлений и
состояний материи, характеризующая длительность их бытия.
Единица времени – секунда (с). Секунда – продолжительность 9 192 631 770
периодов колебаний излучения, соответствующего переходам между двумя
уровнями сверхтонкой структуры основного состояния атома цезия-133.

11. Основные величины и единицы измерения Международной системы единиц (СИ)

Сила электрического тока (размерность – I) – скалярная величина,
равная производной по времени от электрического заряда,
переносимого носителями заряда сквозь рассматриваемую
поверхность.
Единица силы электрического тока – ампер (А). Ампер – сила
неизменяющегося тока, который при прохождении по двум
параллельным прямолинейным проводникам бесконечной длины с
ничтожно малой площадью кругового поперечного сечения,
расположенным в вакууме на расстоянии 1 м один от другого,
вызывал бы на каждом участке проводника длиной 1 м силу
взаимодействия, равную 2 10-7 Н.
Новое определение ампера:
1 ампер - электрический ток, соответствующий потоку 1/1,6021766208 ×
10−19 элементарных электрических зарядов в секунду. Для выражения единицы
требуется заряд электрона.

12. Основные величины и единицы измерения Международной системы единиц (СИ)

Термодинамическая температура (размерность – T) – температура,
отсчитываемая по термодинамической шкале температур от абсолютного нуля.
Единица термодинамической температуры – кельвин (К). Кельвин равен
1/273,16 части термодинамической температуры тройной точки воды.
Новое определение кельвина:
1 кельвин соответствует изменению тепловой энергии на 1,38064852 × 10−23 джоулей.
Для выражения единицы требуется постоянная Больцмана.

13. Основные величины и единицы измерения Международной системы единиц (СИ)

Количество вещества (размерность n) – величина, равная числу
структурных элементов, содержащихся в теле или системе тел.
Единица количества вещества – моль (моль). Моль равен количеству
вещества, в составе которого содержится столько же структурных
элементов, сколько атомов в изотопе углерода-12 массой 0,012 кг.
Новое определение моля:
1 моль - количество вещества системы, которая содержит 6,022140857 ×
1023специфицированных структурных единиц. Для выражения единицы
требуется постоянная Авогадро (число Авогадро).
Сила света (размерность – J) – величина, равная отношению светового
потока, распространяющегося от источника излучения в
рассматриваемом направлении внутри малого телесного угла к этому
телесному углу.
Единица силы света – кандела (кд). Кандела равна силе света в
данном направлении источника, испускающего монохромати-ческое
излучение частоты 540 1012 Гц ( = 555 нм), энергетическая сила
светового излучения которого в этом направлении составляет 1/683
Вт/ср.

14. Дополнительные величины и единицы

Плоский угол α – геометрическая фигура, образованная двумя
лучами (сторонами угла), выходящими из одной точки. Размерности
не имеет, единица – радиан (рад). Радиан – плоский угол между
двумя радиусами окружности, длина дуги между которыми равна
радиусу.
Телесный угол – часть пространства, заключенного внутри одной
полсти конической поверхности с замкнутой направляющей.
Размерности не имеет, единица – стерадиан (ср). Стерадиан равен
телесному углу с вершиной в центре сферы, вырезающему на ее
поверхности площадь, равную площади квадрата со стороной,
равной радиусу сферы.

15.

Механика – наука о движении и
равновесии тел.
Под движением в механике понимают
простейшую форму изменение материи –
перемещение тела относительно других тел.
или
Движением
называют
изменение
относительного
положения
тела
в
пространстве с течением времени.

16. Механика: от Ньютона до Эйнштейна

Исаак Ньютон
(1643 – 1727)
Альберт Эйнштейн
(1879 – 1955)

17.

Архимед
(ок.272-212 до н.э.
Иоганн Кеплер
(1571-1630)
Галилео Галилей
(1564-1642)
Христиан Гюйгенс
(1629-1695)

18.

2. Кинематика
материальной точки

19.

Кинема́ тика – раздел механики, изучающий
математическое описание движения
идеализированных тел, без рассмотрения
причин движения (массы, сил и т. д.).
Исходные понятия кинематики –
пространство и время.

20.

Пространство и время в физике определяются в общем виде
как фундаментальные структуры координации материальных объектов и их состояний: система отношений, отображающая координацию
сосуществующих объектов (расстояния, ориентацию и т. д.), образует
пространство, а система отношений, отображающая координацию
сменяющих друг друга состояний или явлений (последовательность,
длительность и т. д.), образует время.
Пространство и время являются организующими структурами
различных уровней физического познания и играют важную роль в
межуровневых взаимоотношениях.
Под временем понимается свойство материальных процессов
иметь определенную длительность, следовать друг за другом в
определенной последовательности и развиваться по этапам и
стадиям.

21. Система отсчета

Система отсчёта – это совокупность тела отсчёта, связанной с
ним системы координат и системы отсчёта времени, по
отношению к которым рассматривается движение (или
равновесие) каких-либо материальных точек или тел.

22. Материальная точка

Материальной точкой называется макроскопическое тело,
размеры которого настолько малы, что в рассматриваемом
движении их можно не принимать во внимание и считать, что
все вещество тела сосредоточено в одной геометрической
точке пространства.
За материальную точку принимают тело, размеры которого
пренебрежимо малы в сравнении с расстояниями между
телами.

23. Материальное тело

Материальное тело – совокупность материальных точек,
которые могут быть идентифицированы и отличны друг от
друга.
Абсолютно твердое тело – тело, расстояние между любыми
точками которого неизменно.

24. Основные системы координат на плоскости

Полярная
система координат
Декартова (прямоугольная)
система координат
Преобразование от полярных координат к декартовым
x cos
y sin

25. Основные системы координат в пространстве

Декартова (прямоугольная)
система координат
Сферическая
система координат
Цилиндрическая
система координат
Преобразование координат
От цилиндрических к декартовым
От сферических к декартовым
x cos ; y sin ; z z
x r sin cos ; y r sin sin ; z r cos

26.

r x ex y e y z ez
r r (t )
x x(t ) ; y y (t ) ; z z (t )
dx
dy
dz
v e x e y e z vxe x v y e y vz e z
dt
dt
dt

27. Скорость и ускорение при прямолинейном движении

x1 x(t )
x2 x(t t )
x x2 x1 x(t t ) x(t )
x x(t t ) x(t )
t
t
Средняя скорость
ср
Мгновенная скорость
lim
Ускорение
a lim
x dx
x
t 0 t
dt
d
x
t 0 t
dt

28. Примеры

Пример 1. Неподвижная материальная точка.
Пример 2. Равномерное движение.
x Bt C ;
B, C const
x(t ) x0 0 t
dx
B ср
dt
C x(t 0) x0
s x x0 Bt
a 0
0 const
a 0
x const
x 0
x 0
a 0

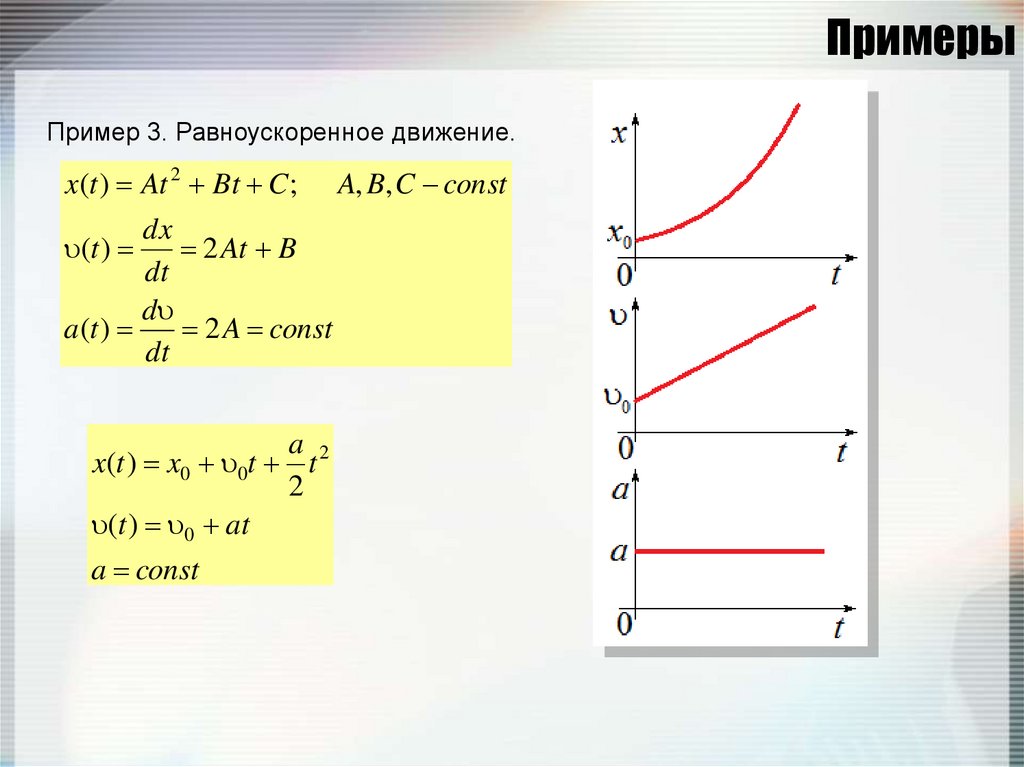
29. Примеры

Пример 3. Равноускоренное движение.
x(t ) At 2 Bt C ;
dx
2 At B
dt
d
a(t )
2 A const
dt
(t )
a 2
x(t ) x0 0t t
2
(t ) 0 at
a const
A, B, C const

30. Движение по окружности

Угловая координата
(t )
Угловая скорость
d
dt
Угловое ускорение
d d 2
2
dt dt
Равномерное вращение:
const угловая скорость ( угловая или круговая частота вращения) [c 1 ]
(t ) t 0
число оборотов в единицу времени (частота вращения) [ Гц]
2
1 2
T
период вращения [c]

31. Связь угловых и линейных величин при вращении

S – длина дуги окружности XM
R – радиус окружности
ds
линейная скорость
dt
d 2s
a 2 линейное ускорение
dt
s R
R
R
a

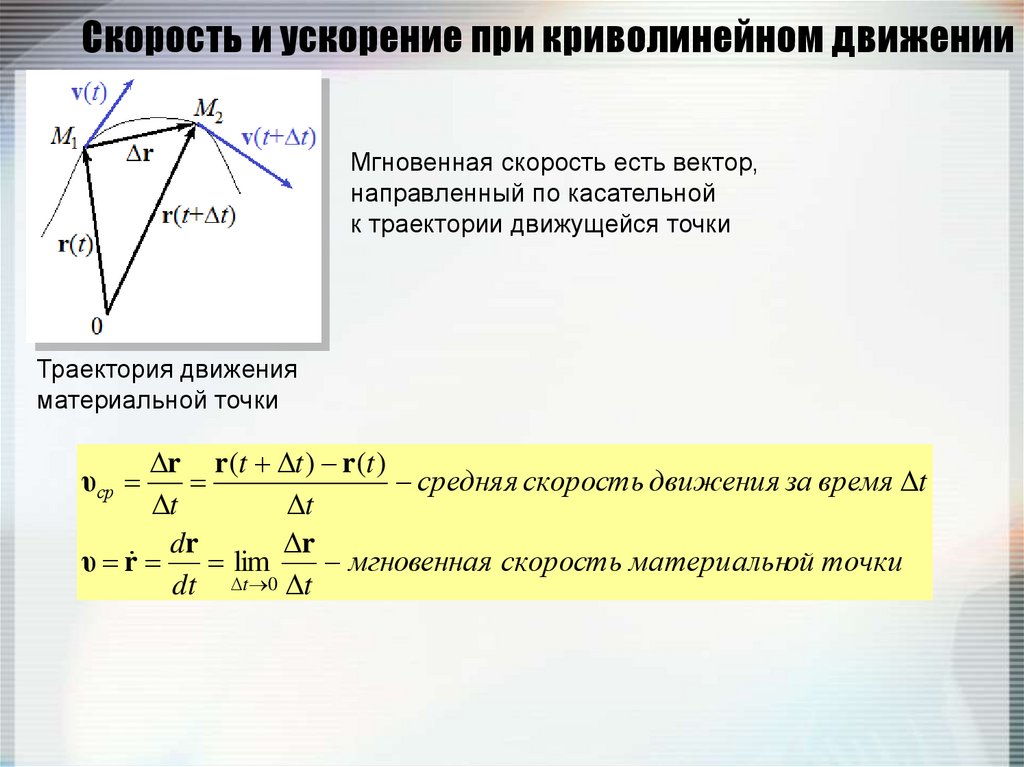
32. Скорость и ускорение при криволинейном движении

Мгновенная скорость есть вектор,
направленный по касательной
к траектории движущейся точки
Траектория движения
материальной точки
r r (t t ) r (t )
средняя скорость движения за время t
t
t
dr
r
υ r
lim
мгновенная скорость материальной точки
t
0
dt
t
υср

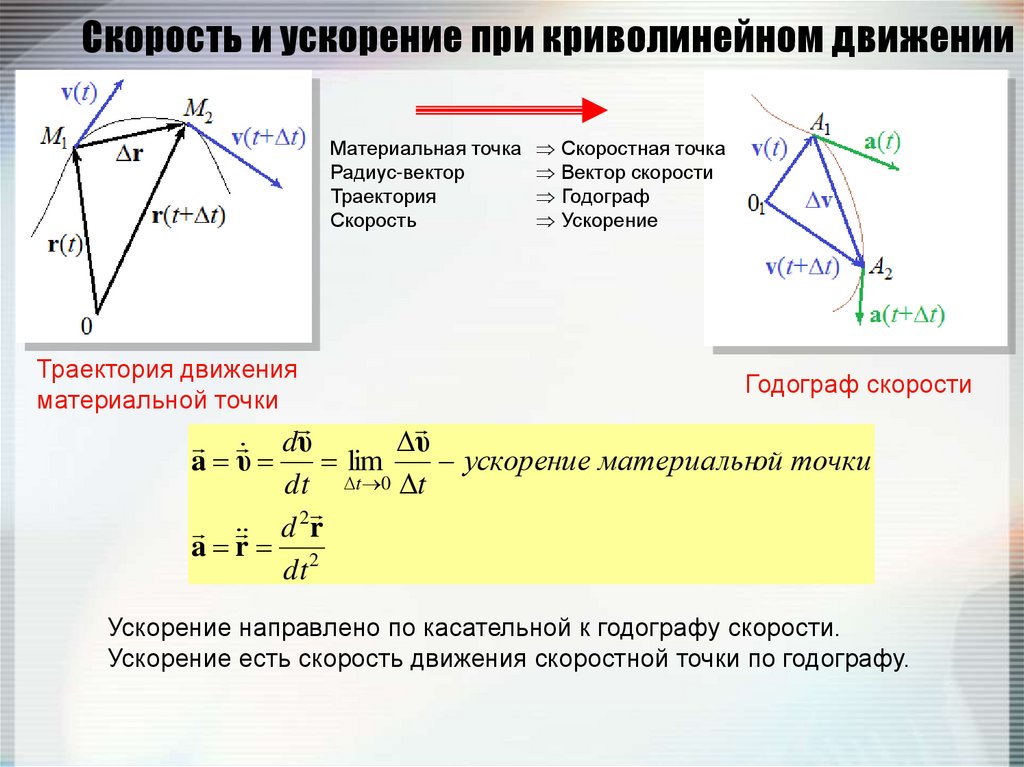
33. Скорость и ускорение при криволинейном движении

Материальная точка
Радиус-вектор
Траектория
Скорость
Траектория движения
материальной точки
Скоростная точка
Вектор скорости
Годограф
Ускорение
Годограф скорости
dυ
υ
a υ
lim
ускорение материальной точки
dt t 0 t
d 2r
a r 2
dt
Ускорение направлено по касательной к годографу скорости.
Ускорение есть скорость движения скоростной точки по годографу.

34. Скорость и ускорение при криволинейном движении

dv d
dτ
d
a
( τ ) τ
dt dt
dt
dt
dτ dτ ds n
,
dt ds dt R
где R называется радиусом кривизны
траектории
2 d
a n τ
an a
R
dt
Ускорение можно представить в виде геометрической суммы
нормального и тангенциального (касательного) ускорений.
При равномерном движении по окружности тангенциальное ускорение
отсутствует, а нормальное ускорение называется центростремительным.
2
aцс 2 R
R

35. Векторы угловой скорости и углового ускорения при движении по окружности

v ω r
a v ω r ω r ω r ω v
Эти формулы справедливы только в случае,
когда ось вращения не изменяет своего
направления в пространстве
2
a an2 a 2 R 4

36.

3. Динамика
материальной точки.
Законы Ньютона
Динамика – раздел механики, изучающий движение тел совместно
с физическими причинами, вызывающими это движение

37. Понятие силы

В динамике Ньютона не скорость, а изменение скорости, т. е. ускорение,
имеет причину. Причиной изменения скорости является сила.
Задача заключается в том, чтобы дать количественную формулировку
соотношения между силой и ускорением. Эта задача решается законами
движения Ньютона.
Силы не являются какими-то самостоятельными сущностями, независимыми
от материальных тел. Они создаются материальными телами. Поэтому можно
сказать, что посредством сил материальные тела действуют друг на друга, т.е.
взаимодействуют. Сила при этом выступает как количественная мера
интенсивности взаимодействий тел, проявляющаяся в изменении их
количества движения (импульса).
Сила является векторной величиной. Единица измерений – Ньютон (Н).
1 Н = 1 кг м с-2
Если на тело воздействуют несколько сил (при взаимодействии с несколькими
телами), то находится результирующая (суммарная) векторная сила.

38. Виды силовых взаимодействий

1.Гравитационное
2. Электромагнитное
3. Сильное
4. Слабое
Сильные и слабые взаимодействия проявляются в атомных ядрах и в мире
элементарных частиц. Они действуют на малых расстояниях: сильные – на
расстояниях ~10-15 м, слабые – на расстояниях ~10-18 м.
Гравитационные и электромагнитные силы являются дальнодействующими.

39. Первый закон Ньютона (закон инерции)

Тело (материальная точка), не подверженное
воздействиям, либо находится в покое, либо
прямолинейно и равномерно.
внешним
движется
Свободным называется тело, на которое не действуют внешние силы или
их действие скомпенсировано для любого момента времени.
Движение свободного тела называется свободным или движением по
инерции.
Свободные тела являются абстракцией.

40. Инерциальные системы отсчета

В кинематике выбор системы отсчета не существенен. Все системы отсчета
кинематически эквивалентны. В динамике выбор системы отсчета важен.
Существует система отсчета, в которой все свободные тела
движутся прямолинейно и равномерно. Такая система
называется инерциальной системой отсчета (ИСО).
Строго инерциальных систем отсчета не существует.
Система отсчета, движущаяся с ускорением относительно ИСО, является
неинерциальной

41. Масса

Свойство тел оказывать сопротивление при попытках
привести его в движение или изменить модуль или
направление его скорости называется инертностью.
Масса
(инертная
масса)
тела
количественной мерой его инертности.
Единица измерения в СИ: килограмм (кг).
является

42. Изолированная (замкнутая) система

Изолированная (замкнутая) система – это система
материальных тел, на которые не действуют внешние
силы.
В такой системе тела могут взаимодействовать только между собой.
Пусть замкнутая система состоит из двух взаимодействующих между собой
материальных точек, движущихся со скоростями, малыми по сравнению со
скоростью света (нерелятивистский случай). В этом случае отношение масс
двух материальных точек равно взятому с противоположным знаком
отношению приращений скоростей этих точек в результате взаимодействия
между ними.
m1
2
m2
1

43. Импульс материальной точки

Импульсом (количеством движения) материальной точки
называется вектор, равный произведению массы материальной
точки на её скорость:
p mv
Импульсом системы материальных точек называется
векторная сумма импульсов отдельных материальных точек, из
которых состоит эта система:
p p1 p 2 p N m1v1 m2 v 2 mN v N
Закон сохранения импульса:
Импульс изолированной системы материальных точек сохраняется,
т.е. остается постоянным во времени, каково бы ни было
взаимодействие между ними.

44. Второй закон Ньютона

Качественное определение силы:
Под силой в механике понимают всякую причину, изменяющую
импульс движущегося тела.
В инерциальной системе отсчета производная импульса
материальной точки по времени равна действующей на
неё силе
dp d
p
(mv) F
dt dt
dp d
d
v
Если m=const, то F
(mv) m ma mv m r
dt dt
dt
F
a
m
dp d dm
dv dm
Если m const, то F
(mv)
v m
v ma m r mr
dt dt
dt
dt dt

45. Третий закон Ньютона

Рассмотрим замкнутую систему двух взаимодействующих точек.
Закон сохранения импульса в этом случае:
p1 p 2 const
Дифференцируем по времени:
p1 p 2 0
На основании 2-го закона Ньютона:
F1 F2 0
F1 F2
Сила взаимодействия двух материальных точек равны по модулю,
противоположно направлены и действуют вдоль прямой,
соединяющей эти материальные точки.
Силы F1 и F2 приложены к разным телам!

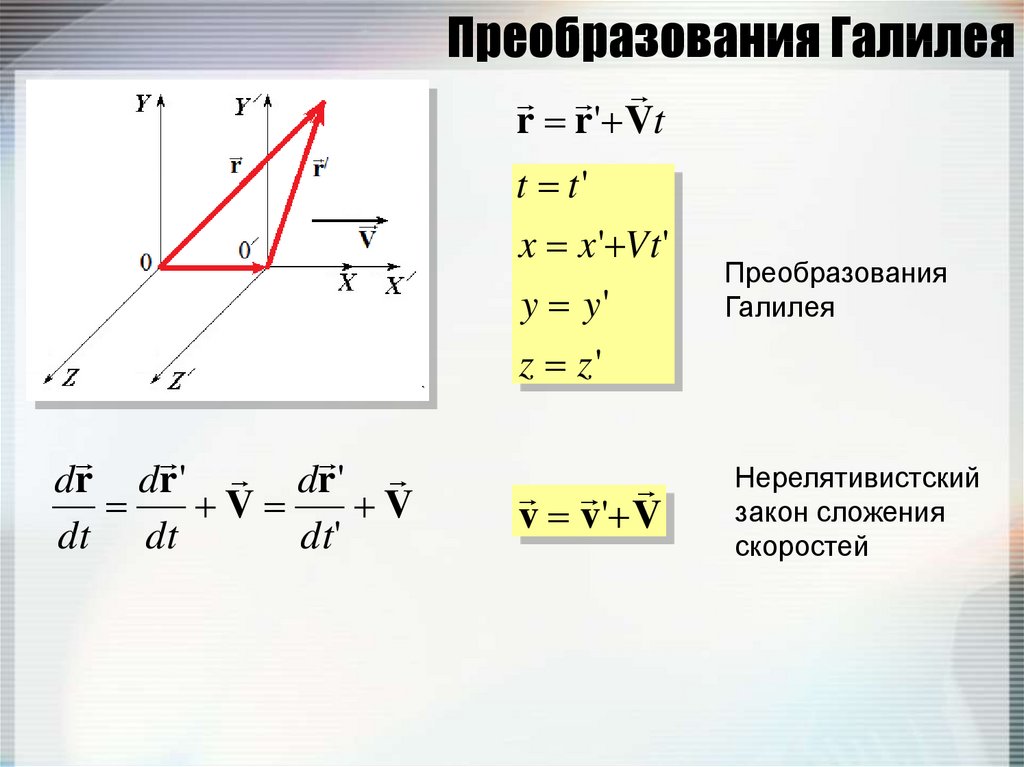
46. Преобразования Галилея

r r ' Vt
t t'
x x ' Vt '
y y'
z z'
dr dr '
dr '
V
V
dt dt
dt'
v v' V
Преобразования
Галилея
Нерелятивистский
закон сложения
скоростей

47. Принцип относительности Галилея

dv dv' dv'
dt dt dt'
a a'
Ускорение инвариантно относительно преобразований Галилея
ma' F'
Сила инвариантна относительно преобразований Галилея
Принцип относительности Галилея:
Уравнения механики Ньютона инвариантны относительно
преобразований Галилея.
или
Все механические явления в различных инерциальных
системах отсчета протекают одинаковым образом, вследствие
чего
никакими
механическими
опытами
невозможно
установить, покоится данная система отсчета или движется
прямолинейно и равномерно.

48.

4. Система материальных точек
Под системой материальных точек (СМТ) будем понимать
конечное число взаимодействующих тел, которые можно
считать материальными точками.

49. Внешние и внутренние силы

Внешние силы – силы, действующие на СМТ со стороны тел,
не входящих в рассматриваемую СМТ.
(e)
Внутренние
силы
–
силы,
действующие
материальными точками, входящими в СМТ.
(i)
между
3-й закон Ньютона позволяет выполнить переход от механики
отдельной материальной точки к механике СМТ.
Геометрическая сумма всех внутренних сил, действующих в
СМТ, равна нулю:
(i ) (i )
(i )
F1 F2 Fn 0

50. Внешние и внутренние силы

Из 2-го закона Ньютона следует:
Импульсом
СМТ
называется векторная сумма
импульсов
материальных
точек, ее составляющих.
d
p1 p 2 p n
dt
(e) (e)
(e)
F1 F2 Fn
dp
F (e)
dt
dp1 (i ) ( e )
F1 F1 ;
dt
dp 2 ( i ) ( e )
F2 F2 ;
dt
............................
Производная по времени от импульса
СМТ равна геометрической сумме всех
внешних сил, действующих на систему.
Уравнение движения СМТ
Если геометрическая сумма внешних сил, действующих на СМТ, равна
нулю, то импульс СМТ сохраняется, т.е. не меняется со временем.
(Частный случай – замкнутая система)

51. Импульс силы

dp
F (e)
dt
Если сила F(e) постоянная, то
(e)
p p0 F (t t0 )
Произведение постоянной силы F(e) на время ее действия называется
импульсом силы за это время.
Общий случай:
p p0 lim
t 0
t
(e)
(e)
F
t
F
i i ( )d
n
i 1
t0
Приращение импульса СМТ равно импульсу геометрической суммы
всех действующих на нее внешних сил.

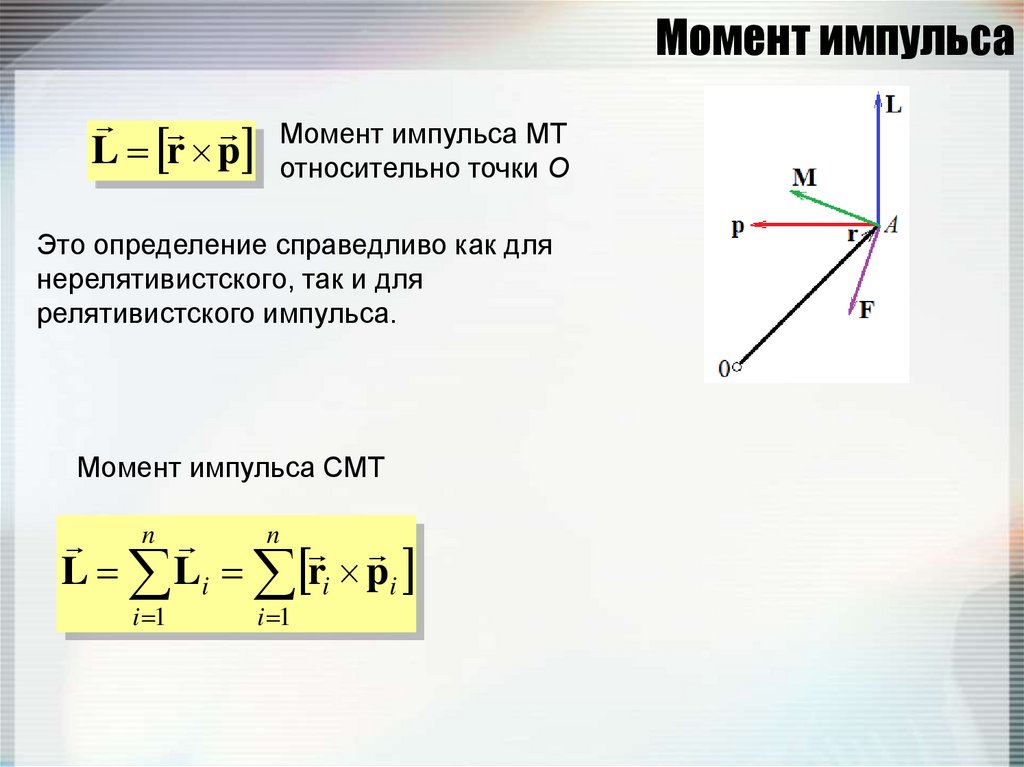
52. Момент импульса

L r p
Момент импульса МТ
относительно точки О
Это определение справедливо как для
нерелятивистского, так и для
релятивистского импульса.
Момент импульса СМТ
n
n
L Li ri pi
i 1
i 1

53. Момент силы

Момент силы, действующей на МТ,
относительно точки О
M r F
Момент силы, действующей на СМТ
n
n
M Mi ri Fi
i 1
i 1
Fi – полная сила, приложенная к i-ой материальной точке
(e)
M Mi ri Fi ri Fi
i
i
i
i
(in )
ri Fij
j
(in ) 1
(in ) (in ) 1
ri Fij 2 ri Fji rj Fij 2 ri rj Fji
i
j
i
j
(in )
(in )
1
(in )
(in )
(ri r j ) // Fij (ri r j ) Fij 0
Fij Fji 0
2 i j

54. Момент силы, действующей на СМТ

n
n
(e)
M Mi ri Fi
i 1
i 1
В механике Ньютона требование о равенстве нулю момента
внутренних сил СМТ принимается как постулат, дополнительный к
законам Ньютона. Только при этом условии можно считать момент сил
сводящимся к моменту внешних сил.
Существуют ситуации, когда момент внутренних сил отличен от нуля.
Например, при внутреннем взаимодействии системы движущихся зарядов 3-й
закон Ньютона не выполняется

55. Уравнение моментов для материальной точки

L r p ;
r r (t );
p p(t )
dL dr dp
p r v p r F 0 r F
dt dt
dt
Уравнение моментов для материальной точки
Уравнение моментов для материальной точки не является
независимым законом движения, а следует из законов Ньютона.
dL
M
dt
Для СМТ:
dL
dri
dpi
Li pi ri
0 ri Fi Mi M
dt
dt
i
i
i dt
i
i
Уравнение моментов для СМТ
Уравнение моментов для СМТ требует дополнительного
независимого от законов Ньютона предположения о
центральности внутренних сил.
dL
M
dt

56. Центр масс СМТ

В нерелятивистском случае (mi=const) можно ввести понятие центра масс СМТ
dri d
d 1
p mi v i mi
mi ri m mi ri
dt dt i
dt m i
i
i
где m mi масса СМТ как сумма масс МТ.
i
R
miri
i
mi
miri
i
m
i
Радиус-вектор, определяющий центр
масс (центр инерции) СМТ

57. Теорема о движении центра масс СМТ

Скорость движения центра масс:
Импульс СМТ:
Уравнение движения:
dR
V
dt
dR
p m
mV
dt
dV
m
F
dt
Теорема о движении центра масс СМТ:
Уравнение движения СМТ эквивалентно уравнению движения
материальной точки, вся масса которой сосредоточена в центре масс,
а все внешние силы, действующие на точки системы, приложены к ее
центру масс.

58. Движение в системе двух взаимодействующих частиц (Задача двух тел. Приведенная масса)

Рассмотрим замкнутую систему, состоящую из 2-х МТ.
2
Уравнения движения этих точек:
d r1 F1
d 2r2
dt
m1
;
F2
dt
m2
По 3-му закону Ньютона: F1 F2
2
d
F2 F1 1
1 Это уравнение описывает движение
r r1 F2
2 2
m2 m1
dt
m1 m2 одной МТ относительно другой.
r r2 r1 - радиус-вектор, проведенной от первой точки ко второй.
m1m2
m1 m2
Приведенная масса
Уравнение движения
2
d r
2 F2
dt
Задача о движении двух материальных точек распадается на 2 независимые
задачи:
1) Определение равномерного движения ЦМ.
2) Определение относительного движения одной МТ относительно другой.

59.

5. Законы сохранения в механике
Законы сохранения позволяют рассмотреть общие свойства
движения без решения уравнений и детальной информации о
развитии процессов во времени.
Законы сохранения отвечают на вопрос о
последовательности
физических
ситуаций,
уравнениями движения, остается неизменным
том, что в
описываемой

60. Сохраняющиеся величины

Для замкнутых систем существуют интегралы движения – функции
координат и скоростей частиц, входящих в систему, которые
сохраняют при движении постоянные значения.
Для системы N частиц, между которыми нет жестких связей, их может
быть 6N – 1.
Аддитивные интегралы движения:
• энергия
• импульс
• момент импульса
Они подчиняются законам сохранения.
В основе закона сохранения энергии – однородность времени.
В основе закона сохранения импульса – однородность пространства.
В основе закона сохранения момента импульса – изотропия пространства.

61. Закон сохранения импульса

Изолированная (замкнутая) система – это система
материальных тел, на которые не действуют внешние
силы.
dp
p const
F 0
dt
0
Закон сохранения импульса
p x const ; p y const ; p z const
Для МТ закон сохранения импульса означает, что в отсутствие внешних сил она
движется с постоянной скоростью по прямой линии.
Для СМТ в нерелятивистском случае закон утверждает, что центр масс системы
движется равномерно и прямолинейно
В случае наличия внешних сил выбором системы координат можно
добиться того, что одна или две проекции внешних сил обращаются в
нуль. Тогда не весь импульс сохраняется, а только соответствующие
его проекции, в направлении которых проекции внешних сил нулевые.

62. Закон сохранения момента импульса

Для изолированных систем момент внешних сил равен нулю и
уравнение моментов примет вид:
Интегрируем:
L const
dL
0
dt
Lx const ; Ly const ; Lz const

63. Кинетическая энергия

Рассмотрим систему, состоящую
из одной материальной точки.
Уравнение движения: mv
F
Умножим на перемещение d s vdt
mvvdt Fds
2
m 2
m 2
Fd s
mvvdt mvdv m d d
d
2
2
2
m 2
0
Система замкнута F 0 d
2
m 2
T
кинетическая энергия материальной точки
2
2
В случае изолированной частицы кинетическая энергия
p
является интегралом движения. В случае нескольких
T
2m взаимодействующих частиц кинетическая энергия входит
как слагаемое в аддитивный интеграл движения.

64. Работа

Если на МТ действует сила F, кинетическая энергия не постоянна.
Приращение кинетической энергии за время dt равна Fds,
где ds - перемещение МТ за это же время.
dA=Fds=F ds cos Работа, совершаемая силой F на пути ds
- угол между направлением силы и направлением перемещения
точки приложения силы.
Работа характеризует изменение энергии, обусловленное действием
силы на МТ.
2
A Fd s Fs ds
2
1
1
A A12 T2 T1
Работа силы F на пути 1-2
Работа результирующей всех сил, действующих на МТ, идет на приращение кинетической
энергии МТ

65. Работа. Мощность

ПРИМЕР.
Закон Гука
Fупр kx
Работа, которую нужно
совершить, чтобы вызвать
удлинение пружины х
kx 2
A
2
Работа, совершаемая в единицу времени, называется мощностью:
dA
P
dt
P F v

66. Консервативные силы

Если МТ в каждой точке пространства подвержена воздействию других
тел, то говорят, что эта частица находится в поле сил.
F=F(r) – центральное поле сил
Если во всех точка поля силы одинаковы по величине и направлению,
поле называется однородным.
Поле, изменяющееся со временем – нестационарное поле.
Поле, постоянное во времени - стационарное поле.
Если для стационарного поля работа, совершаемая над частицей
силами поля, зависит лишь от начального и конечного положения
частицы и не зависит от пути, по которому движется частица, то такие
силы называются консервативными.
Работа консервативных сил на замкнутом пути равна нулю.

67. Потенциальная энергия во внешнем поле сил

Поле консервативных сил является частным случаем потенциального
силового поля. Поле сил называется потенциальным, если его можно
записать с помощью потенциальной энергии так, что:
U U U
F U gradU
ex
ey
ez
x
y
z
U – потенциальная энергия.
Если потенциальная энергия не зависит от времени, потенциальное
поле будет стационарным, а его силы – консервативными.
A12 U1 U 2
A T2 T1 U1 U 2
T2 U 2 T1 U1
Полная механическая энергия частицы
E T U

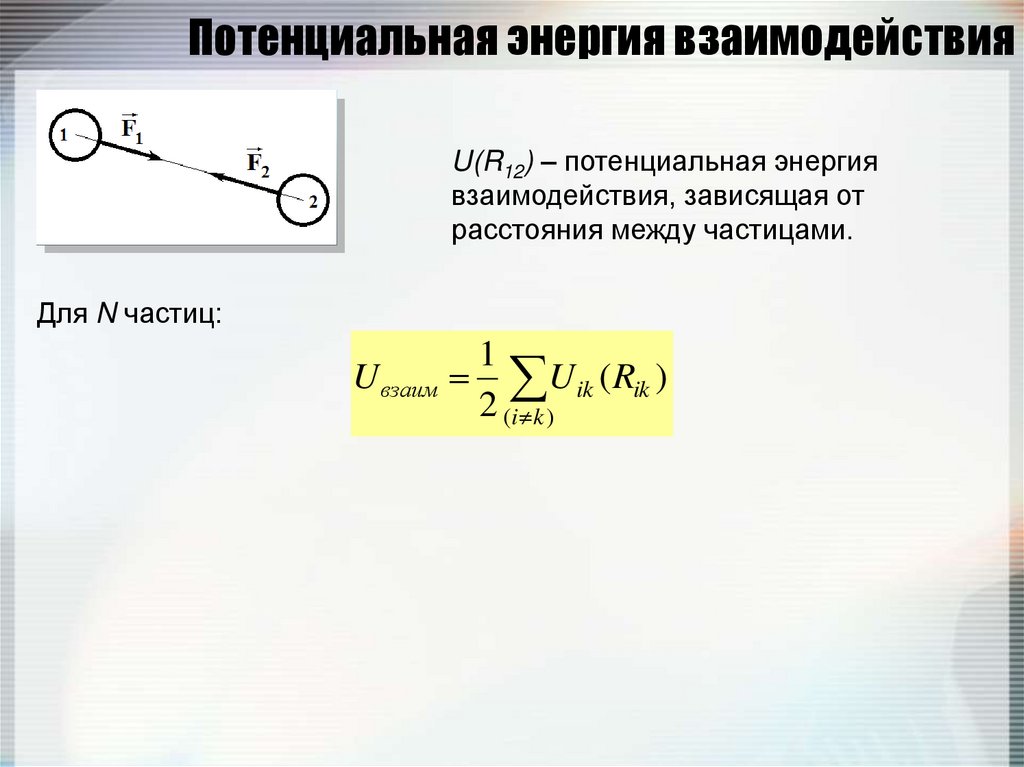
68. Потенциальная энергия взаимодействия

U(R12) – потенциальная энергия
взаимодействия, зависящая от
расстояния между частицами.
Для N частиц:
1
U взаим U ik ( Rik )
2 (i k )

69. Закон сохранения энергии

Полная механическая энергия системы тел, на которые действуют
только консервативные силы, остается постоянной
E T U взаим U внешн const
Полная механическая энергия замкнутой системы тел, между
которыми действуют только консервативные силы, остается
постоянной
E T U взаим const

70.

6. Неинерциальные
системы отсчета
Неинерциальной системой отсчета (НСО) называется система,
движущаяся ускоренно относительно инерциальной.
Тело отсчета принимается за абсолютно твердое тело.
Простейшими НСО являются системы отсчета, движущиеся
ускоренно прямолинейно и вращающиеся системы.

71. Силы инерции

В ИСО единственной причиной ускоренного движения тела являются силы,
действующие со стороны других тел. Силы – результат взаимодействия тел.
В НСО можно ускорить тело простым изменением состояния движения
системы отсчета.
В НСО существуют ускорения, которые не связаны с силами взаимодействия
тел, рассматриваемыми в ИСО.
В НСО 1-й и 3-й законы Ньютона не имеют физического смысла.
2-й закон Ньютона можно формулировать без изменений, но наряду с силами
взаимодействия, необходимо учесть силы инерции, обусловленные
ускорением НСО относительно ИСО.
ma' F Fин
ma F
a’ – ускорение в НСО (относительное ускорение), a – ускорение в
ИСО (абсолютное ускорение), F - «обычные» силы взаимодействия,
Fин – силы инерции
Fин m(a' a)
Силы инерции обуславливают разность между относительным и
абсолютным ускорениями. Силы инерции существуют только в НСО.

72. НСО, движущиеся прямолинейно-поступательно

r r0 r'
r r r '
Дифференцируем по
времени.
0
r r0 r '
a a 0 a'
a’ – ускорение в НСО (относительное ускорение), a – ускорение в
ИСО (абсолютное ускорение), a0 – ускорение НСО относительно
ИСО (переносное ускорение)
Fин m(a' a) ma0
Fин ma0
Сила инерции направлена противоположно переносному ускорению НСО.
ma' F ma0
- основное уравнение динамики МТ с НСО при
поступательном движении

73. Неинерциальные вращающиеся системы отсчета

v ω r
dr
ω r
dt
Отличие вращающихся НСО обуславливается тем, что переносная
скорость различных точек вращающейся системы координат
различна.
v v' v 0
Для абсолютного ускорения все сложнее. Если даже относительная
скорость МТ при движении не меняется, МТ должна испытывать
ускорение, отличное от переносного.
a a0 a' a K
aК – кориолисово ускорение

74. Неинерциальные вращающиеся системы отсчета

/
/
/
Дифференцируем по времени
r ex x e y y ez z
v r v' v 0 v' ,
где r v 0 переносная скорость
/ / / / / /
v' e x v x e y v y e z v z относительная скорость
Находим абсолютное ускорение:
/
/
/
/
d
e
dv' dv /x / dv y / dv /z /
d
e
d
e
ex
ey
e z v /x x v /y y v /z z a' v'
dt
dt
dt
dt
dt
dt
dt
dv dr dv'
a
v 0 v' a' v'
dt
dt dt
a K 2 v' кориолисов о ускорение
2
a0 r ( r ) r
2
2
(d r ) R переносное ускорение
a a0 a' a K

75. Силы инерции

Пусть неинерциальная система К’ вращается с постоянной угловой скоростью
вокруг оси, перемещающейся поступательно с ускорением а0 относительно
инерциальной К-системы.
2
a
'
a
a
R
2
v
'
Ускорение частицы в К’-системе:
0
Основное уравнение динамики в неинерциальной системе отсчета:
2
ma' F ma0 m R 2m v'
Поступательная сила инерции:
Центробежная сила инерции:
Сила Кориолиса:
Fин ma0
2
Fцб m R
Fкор 2m v'

76.

7. Кинематика абсолютно
твердого тела
Степени свободы абсолютно твердого тела.
Углы Эйлера.
Вращательное движение.
Мгновенная ось вращения

77. Степени свободы твердого тела

Абсолютно твердое тело – неизменяемая система материальных точек, т.е.
идеализированная система, при любых движениях которой расстояния между
материальными точками системы остаются неизменными.
Число независимых функций, которыми можно описать движение СМТ,
называется числом ее степеней свободы.
N материальных точек 3N степеней свободы
На 3N координат налагаются дополнительные условия – связи. Для
однозначного определения положения всех МТ достаточно знать меньшее
число координат f. Остальные 3N-f координат вычисляются из уравнений
связи.
Для этих целей могут быть использованы не только f обычных координат, но и
f любых величин q1, q2, …, qf , заданием которых положение МТ определяется
однозначно. Такие величины называются обобщенными координатами.
Идеально твердое тело, если на его движение не наложены никакие
ограничения, обладает шестью степенями свободы.

78. Углы Эйлера

СК XYZ привязана к твердому телу.
Плоскости 0XY и 0X1Y1 пересекаются
по линии 0K – линии узлов.
Углы Эйлера являются
независимыми переменными и
полностью характеризуют положение
твердого тела, закрепленного в
одной точке.
Углы Эйлера:
K 0 X (0 2 ) угол собственно го вращения
Х 1 0 K (0 2 ) угол прецессии
Z1 0 Z (0 ) угол нутации
(t ); (t ); (t )

79. Кинематика твердого тела

При поступательном движении скорости всех точек тела в любой момент
времени одинаковы. Любая прямая, проведенная между какими-либо точками
тела, перемещается параллельно самой себе.
Углы Эйлера при поступательном движении постоянны.
Поступательно движущееся тело имеет 3 степени свободы.
Плоским называется движение, при котором траектории всех точек лежат в
параллельных плоскостях. Число степеней свободы равно трем.
Вращательное движение – движение, при котором две точки тела остаются
все время неподвижным.
Прямая, проходящая через эти точки, называется осью вращения.
Все точки ТТ, лежащие на оси вращения, неподвижны. Другие точки ТТ
движутся по окружностям в плоскостях, перпендикулярных оси вращения.
Вращательное движение является плоским.

80. Вращательное движение

Угловая координата (t )
Угловая скорость
d
dt
d d 2
Угловое ускорение
2
dt dt
v ω r
Равномерное вращение:
const угловая скорость ( угловая или круговая частота вращения) [c 1 ]
(t ) t 0
число оборотов в единицу времени (частота вращения) [ Гц]
2
1 2
T
период вращения [c]

81. Мгновенная ось вращения

В плоском движении положение ТТ полностью определяется положением
отрезка прямой, жестко связанно с точками тела.
Перемещение этого отрезка можно разложить на:
а) поступательное движение, при которой прямая перемещается параллельно
самой себе;
б) вращательное движение, при котором ТТ поворачивается на угол .
Разложение перемещения на поступательное и вращательное неоднозначно,
но угол поворота при перемещении один и тот же.
v v 0 ω r
Изменяя поступательную скорость, мы одновременно изменяем положение
оси вращения. Любая ось, перпендикулярная плоскости движения, является
осью вращения.
Ось вращения, для которой поступательная скорость равна нулю,
называется мгновенной осью вращения.
С течением времени положение оси вращения меняется относительно тела и
системы координат.

82. Теорема Эйлера

Рассмотрим тело, закрепленное в одной точке.
Теорема Эйлера
Твердое тело, имеющее одну закрепленную неподвижную точку,
может быть из одного положения переведена в любое другое
одним поворотом на некоторый угол вокруг неподвижной оси,
проходящей через точку закрепления.

83.

8. Динамика абсолютно
твердого тела
Уравнения движения твердого тела.
Моменты инерции.
Вычисление моментов инерции относительно оси.
Теорема Гюйгенса-Штейнера.
Кинетическая энергия вращающегося твердого тела.
Уравнения Эйлера.
Симметричный волчок.

84. Движение центра масс твердого тела

Центром масс (центром инерции) СМТ называется точка С, положение
которой задается радиус-вектором rс:
rc
miri
mi
Центр масс твердого тела движется так, как двигалась бы материальная
точка с массой, равной массе тела, под действием всех приложенных к
телу сил:
mac Fi внешн

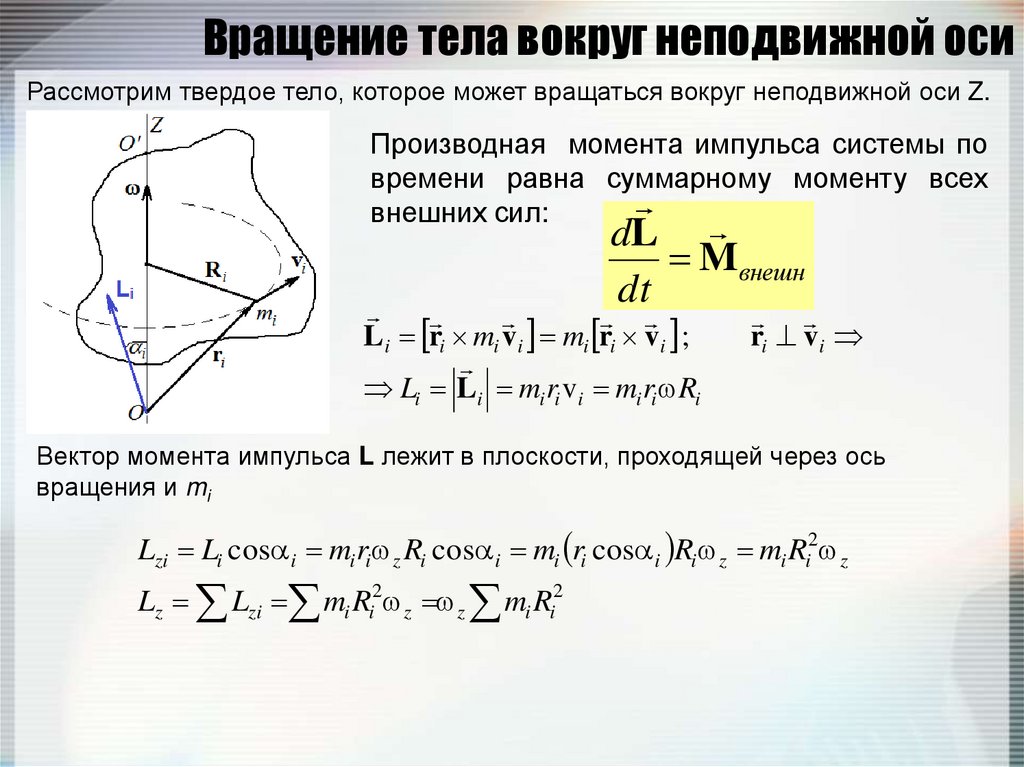
85. Вращение тела вокруг неподвижной оси

Рассмотрим твердое тело, которое может вращаться вокруг неподвижной оси Z.
Производная момента импульса системы по
времени равна суммарному моменту всех
внешних сил:
dL
Mвнешн
dt
Li ri mi v i mi ri v i ;
ri vi
Li Li mi ri vi mi ri Ri
Вектор момента импульса L лежит в плоскости, проходящей через ось
вращения и mi
Lzi Li cos i mi ri z Ri cos i mi ri cos i Ri z mi Ri2 z
Lz Lzi mi Ri2 z z mi Ri2

86. Момент инерции

Величина, равная сумме произведений элементарных масс (масс
материальных точек) на квадраты их расстояний от некоторой оси, называется
моментом инерции тела (системы материальных точек) относительно данной
оси:
2
J mi Ri
Lz J z
Для однородного тела, симметричного относительно оси вращения
(для однородного тела вращения):
L Jω
В случае, когда ось вращения проходит через центр масс тела, значение
момента импульса не зависит от положения на оси вращения точки О,
относительно которой он берется.
Ось, положение которой в пространстве остается неизменным при вращении
вокруг нее тела в отсутствие внешних сил, называется свободной осью тела.

87. Момент инерции

Для тела любой формы и с произвольным распределением массы существуют
три взаимно перпендикулярные, проходящие через центр масс тела оси,
которые могут служить свободными осями; они называются главными осями
инерции тела.
Моменты инерции относительно главных осей называются главными
моментами инерции тела. В общем случае J1 J 2 J 3
Для тел с осевой симметрией два из трех главных моментов инерции
совпадают.
Для тел с центральной симметрией все три главных момента инерции
совпадают.
Если подобных симметрий нет, но соотношения между главными моментами
инерции такие же, то такие тела называются волчками
J1 J 2 J 3 ассиметричный волчок
J1 J 2 J 3 симметричный волчок
J1 J 2 J 3 шаровый волчок

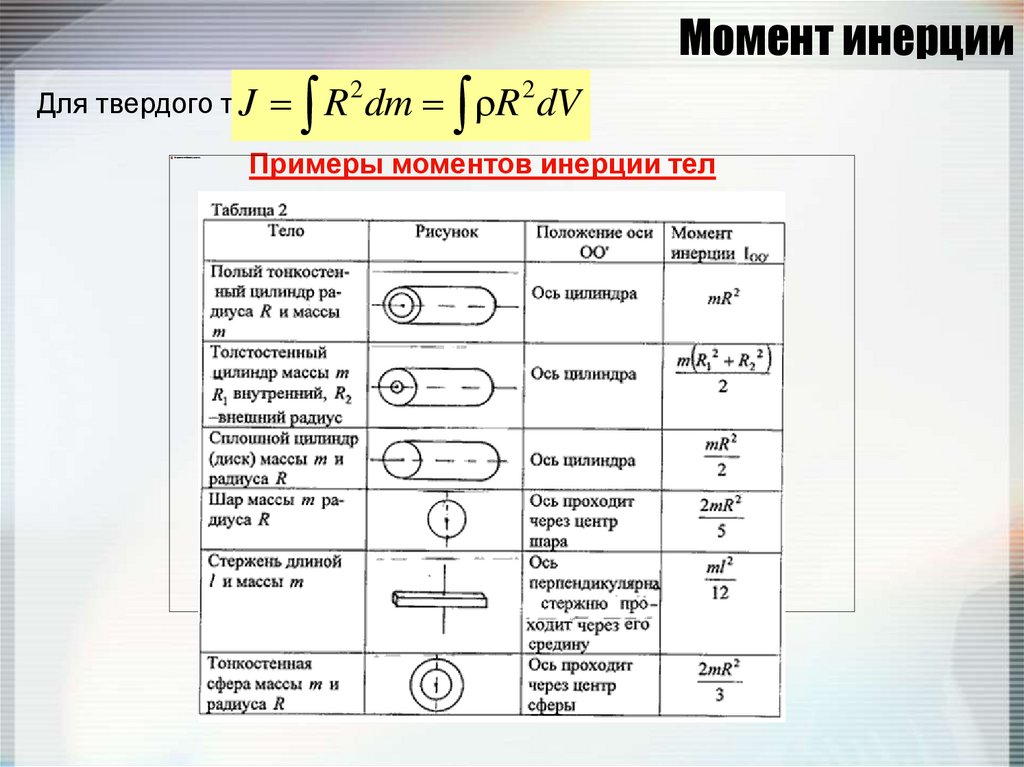
88. Момент инерции

Для твердого тела:
J
2
2
R
dm
R
dV
Примеры моментов инерции тел

89. Теорема Гюйгенса-Штейнера

Момент
инерции
J
относительно
произвольной оси равен сумме момента
инерции
Jc
относительно
оси,
параллельной данной и проходящей
через центр масс тела, и произведения
массы тела m на квадрат расстояния a
между ними:
J J c ma 2

90. Тензор инерции

В общем случае несимметричного тела векторы момента импульса и угловой
скорости не совпадают по направлению и их связь более сложная:
Lx J xx x J xy y J xz z
Ly J yx x J yy y J yz z
Lz J zx x J zy y J zz z
3
Li J ik k ;
(i, k x, y, z 1, 2, 3)
k 1
Тензор инерции:
J xx
J J yx
J zx
J xy
J yy
J zy
J xz
J yz
J zz
В главных осях:
J x
J 0
0
0
Jy
0
0
0
J z

91. Вывод уравнений Эйлера

Рассмотрим движение ТТ около одной закрепленной точки. Мгновенная ось
вращения (и вектор угловой скорости) при этом изменяет направление в
пространстве. Начало СК поместим в точку
Уравнение
закрепления тела.
dv 0
d
движения центра масс тела имеет вид:
m
m
r0 F
dt
dt
В главных осях инерции: L1 J1 1; L2 J 2 2 ; L3 J 3 3
A
A
e
A
e
A
e
Для любого вектора А в выбранной СК:
x x
y y
z z
С течением времени изменяются и проекции вектора А на движущиеся
главные оси, и ориентация главных осей относительно ИСО:
dA
d
e
dA dAx
dA
d
e
d
e
ex
e y y e z z Ax x Ay y Az z
dt
dt dt
dt
dt dt
dt
dei
ei
dt
A
t
dA A
A
dt
t
A
Частная производная вектора А по времени вычисляется в предположении,
что главные оси неподвижны относительно ИСО.

92. Уравнения Эйлера

dL
Учитывая уравнение моментов (уравнение движения)
M , получаем
dt
L
L M
t
В проекциях на оси движущейся СК:
d x
( J z J y ) y z M x
dt
d y
Jy
( J x J y ) y x M y Уравнения Эйлера
dt
d x
Jz
( J y J x ) x y M z
dt
Jx

93. Кинетическая энергия вращающегося твердого тела

1 2
EK J
2
Для плоского движения:
mvc2 J c 2
EK
2
2
Кинетическая энергия тела при плоском движении складывается из
энергии поступательного движения со скоростью, равной скорости
центра масс, и энергии вращения вокруг оси, проходящей через центр
масс тела.

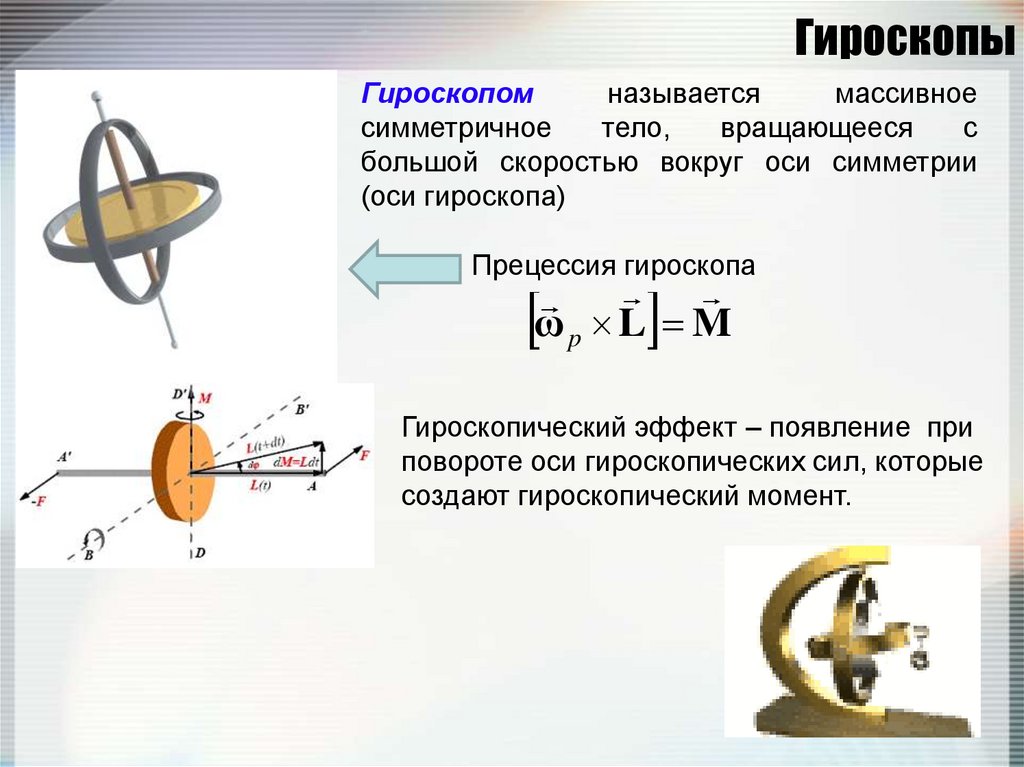
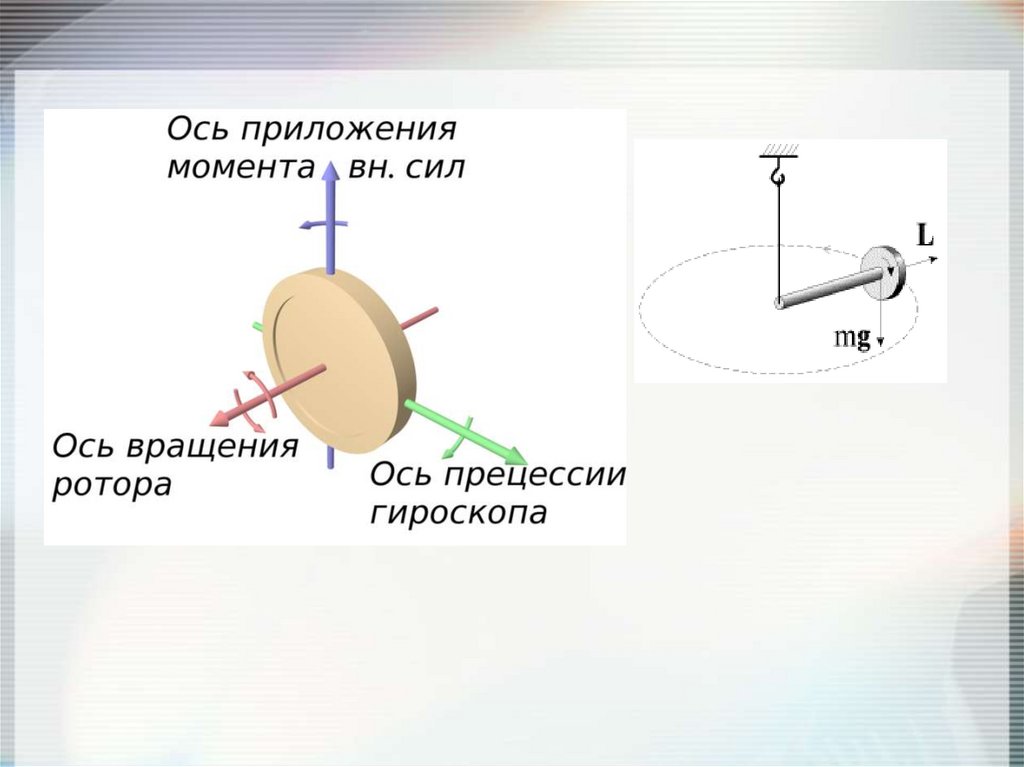
94. Гироскопы

Гироскопом
называется
массивное
симметричное
тело,
вращающееся
с
большой скоростью вокруг оси симметрии
(оси гироскопа)
Прецессия гироскопа
ωp L M
Гироскопический эффект – появление при
повороте оси гироскопических сил, которые
создают гироскопический момент.

95.

96.

9. Движение тела
с переменной массой

97. Реактивное движение

В ракетных двигателях сила тяги создается в результате извержения
продуктов горения топлива в направлении, противоположном силе.
Такая сила реакции называется реактивной, а двигатель –
реактивным.
В общем случае всякий двигатель, создающий тягу, является
реактивным в смысле реализации силы реакции.
Примеры:
пропеллерные
самолеты,
водометные
корабли,
автомобили, железнодорожный транспорт.
Но!
Имеется
существенная
отличительная
особенность
реактивного движения ракеты: в ракетном реактивном двигателе тяга
создается извержением продуктов горения, которые до создания тяги
входят в массу ракеты.
При этом рассматривается движение тел с переменной массой, причем
тяга создается в результате извержения части массы, принадлежащей
телу.

98. Уравнение Мещерского

Ракета в момент времени t имеет массу
M(t), движется со скоростью v, выбрасывает
массу dM / со скоростью u.
Скорости v и u берутся относительно ИСО.
Закон сохранения массы:
dM dM 0;
dM 0
Закон сохранения импульса (для изолированной системы, в моменты
времени t и (t+dt): ( M dM )( v dv) u dM Mv
Пренебрегая бесконечно малым членом второго порядка dvdM, получаем:
Mdv vdM udM 0
d
dM
( Mv) u
dt
dt
Уравнение движения тела с переменной массой,
справедливое, как в релятивистском, так и в
нерелятивистском случае

99. Уравнение Мещерского

В нерелятивистском
случае (малые скорости) применим закон сложения
скоростей: u u v , где u’ – скорость выброшенной массы относительно ракеты:
dv dM dM
M
(u v)
u
dt
dt
dt
Уравнение движения ракеты с
нерелятивистской скоростью в
отсутствие внешних сил
Пусть на ракету действует внешняя сила F. Обозначим расход топлива в
единицу времени через .
dM
dv
M
F u
dt
dt
Уравнение И.В. Мещерского (1859-1935)
(уравнение движения тела с переменной
массой)

100. Формула Циолковского

Рассмотрим ускорение ракеты, движущейся в отсутствие внешних сил
прямолинейно с постоянной скоростью выбрасываемых газов относительно
ракеты:
dv
dM
u
dt
dt
dM
dv
M
u
Интегрируем это равенство:
v v0
ln M ln M 0
u
или
M
v v0 u ln 0
M
M
M M 0e
v v0
u
Формула К.Э. Циолковского (1857-1935)
M0 , v0 - начальные масса и скорость ракеты.

101.

10. Всемирное тяготение

102. Закон всемирного тяготения

Сила, с которой две материальные точки притягиваются друг к другу,
пропорциональна массам этих точек и обратно пропорциональна
квадрату расстояния между ними:
mm
F
1
r
2
2
Коэффициент пропорциональности называется гравитационной постоянной.
6,67 10
11
м3
кг с 2
Гравитационная сила направлена вдоль прямой, проходящей через
взаимодействующие материальные точки.
m1m2
F12 2 e12
r

103. Закон всемирного тяготения

Для определения силы взаимодействия протяженных тел их нужно
разбить на элементарные массы m, каждую из которых можно
принять за материальную точку. i-я элементарная масса тела 1
притягивается к k-й элементарной массе тела 2 с силой:
m m
Fik i 2 k eik
rik
mi mk
eik
Сила, с которой тело 2 действует на тело 1: F12
2
rik
i k
В общем случае
интегрированию.
протяженных
тел
суммирование
сводится
к

104. Гравитационное поле

Гравитационное взаимодействие осуществляется через гравитационное поле. Всякое тело изменяет свойства окружающего его
пространства путем создания в нём гравитационного поля. Это поле
проявляет себя в том, что помещенное в него другое тело массой m
оказывается под действием гравитационной силы F.
Напряжённость гравитационного поля:
Напряженность поля, создаваемого
материальной точкой массы M:
F
G
m
M
G 2 er
r
На материальную точку массы m, находящуюся в точке с радиус-вектором r (от
точечной массы М), со стороны точечной массы M действует сила:
Mm
F Gm 2 er
r
Размерность G совпадает с размерностью ускорения.
Напряженность поля тяготения вблизи поверхности Земли равна ускорению
свободного падения g (без учета вращения Земли вокруг своей оси).

105. Гравитационное поле

Потенциальная энергия взаимодействия масс M и m:
Потенциал гравитационного поля:
Mm
U
r
U
m
Работа поля по перемещению массы m из точки 1 в точку 2:
A12 U1 U 2 m( 1 2 )
F mG
U m
Соотношение между напряженностью и потенциалом гравитационного поля:
G grad
grad
ex
ey
ez
x
y
z

106. Принцип эквивалентности

Опыт Этвеша (1887 г.)
Все физические явления в
однородном поле тяготения
происходят совершенно так же,
как
и
в
соответствующем
однородном поле сил инерции.

107. Космические скорости

Для того, чтобы двигаться вокруг Земли по круговой орбите вблизи радиуса
Земли, тело должно иметь первую космическую скорость:
v12
m
mg v1 gRЗ 8 км / с
RЗ
Для удаления от Земли на расстояние, при котором притяжение Земли
перестает играть существенную роль необходима вторая космическая
скорость:
A U нач U кон
A
M 3m
M m
0 3
R3
R3
M 3m
R3
mg
M 3m
M 3m
mgR3
2
R3
R3
mv 22
mgR3
2
A mgR3
v2 2 gR3 2v1 11 км / с

108. Законы Кеплера

1 закон.
Все планеты движутся по эллиптическим орбитам, причем Солнце
находится в одном из фокусов.
2 закон.
Отрезок, соединяющий Солнце с планетой, описывает за равные
промежутки времени равные площади.
3 закон.
Квадраты времени обращения различных планет вокруг Солнца
относятся как кубы больших полуосей их эллипсов

109.

10. Столкновения

110. Понятие столкновения

Столкновением называется взаимодействие двух или большего
числа материальных тел, частиц и т.д., которое происходит в
относительно малой области пространства в течение относительно
малого промежутка времени, так что вне этой области пространства и
вне этого промежутка времени можно говорить о начальных
состояниях тел и об их конечных состояниях после взаимодействия
как состояниях, в которых эти тела не взаимодействуют.
Столкновение материальных тел называется ударом. Удар
определяется как процесс, при котором изменяются импульсы
соударяющихся тел без изменения их координат.

111. Законы сохранения при столкновениях

Между величинами, характеризующими начальное и конечное
состояния, соблюдаются определенные соотношения, независимые от
детального характера взаимодействия.
n
Закон сохранения импульса:
k
p
p
i j
i 1
j 1
Система должна быть замкнутой. Число частиц, сорт частиц до и после
столкновения могут быть различными. Закон справедлив как в
релятивистском, так и в нерелятивистском случаях.
n
В системе центра масс закон сохранения импульса:
k
p
p
i j 0
i 1
j 1

112. Законы сохранения при столкновениях

Закон сохранения энергии:
Ei вн Ei к E j вн E j к
n
k
i 1
j 1
При столкновении, например, шаров часть кинетической энергии
превращается во внутреннюю, связанную с теплом внутри шара. Взаимная
потенциальная энергия частиц, составляющих шар, относится к внутренней
энергии. Потенциальную энергию взаимодействия между сталкивающимися
шарами учитывать не надо. Кинетическую энергию вращательного движения
удобнее относить к внутренней энергии.
При применении закона сохранения момента импульса надо учитывать, что
тела и частицы могут обладать внутренним моментом импульса.
У макротел он обусловлен вращением. У микрочастиц он называется спином.
n
Закон сохранения момента импульса:
i 1
k
Li вн Li L i вн L i
j 1

113. Упругие и неупругие столкновения

Если внутренняя энергия частиц при столкновении изменяется, то
столкновение называется неупругим, ели не изменяется, то
столкновение упругое.
Если в конечном состоянии вся энергия превращается во внутреннюю,
то такое столкновение называется абсолютно неупругим.

114. Упругие столкновения

Выберем систему координат так,
столкновения покоилась: р2 =0 .
чтобы
вторая
частица
до
p12
p1/ 2 p2/ 2
2m1 2m1 2m2
p1 p1/ p 2/
p1/ p1 p 2/
(p1 p 2/ ) p 2/ 2 (m1 m2 ) / 2m2
p2/
m2
2
p1 cos
m1 m2
(p1 p 2/ ) p1 p2/ cos

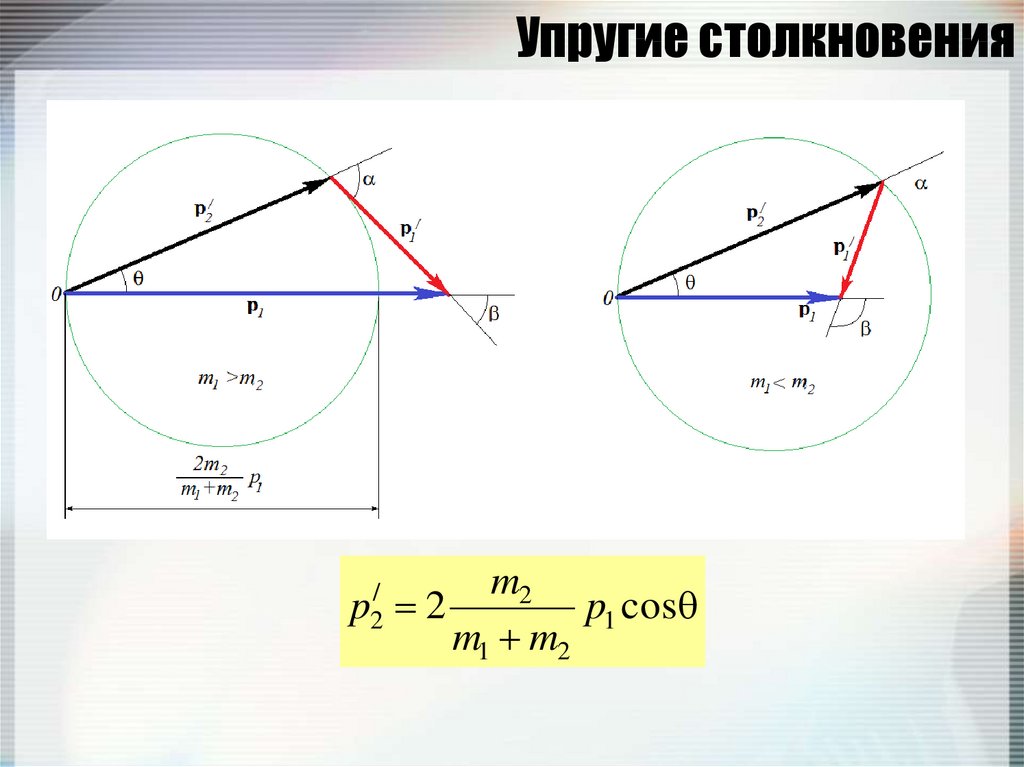
115. Упругие столкновения

p2/
m2
2
p1 cos
m1 m2

116. Лобовое столкновение

Покоящаяся частица получает в результате столкновения максимальный
импульс в том случае, когда 0. В этом случае столкновение называется
лобовым или центральным ударом.
p 2/ 2
m2
p1
m1 m2
EK/ 2
4m1m2
E
2 K1
m1 m2
Максимальная передача энергии происходит при равенстве масс. Первая
частица при этом останавливается, т.е. вся энергия от первой частицы
передается второй.
При значительном различии масс передаваемая энергия очень мала.
EK/ 2
EK/ 2
4m2
EK 1 при m1 m2
m1
4m1
EK 1 при m2 m1
m2
EK/ 2 EK 1

117. Неупругие столкновения

Рассмотрим абсолютно неупругий удар. В этом случае оба тела после удара
сливаются и движутся как единое целое. Пусть второе теле до столкновения
/
/
покоится.
Eвн1 Eвн 2 EK1 Eвн (1 2) EK (1 2)
p1 p(1 2)
m1v1 (m1 m2 ) v 2
v2
m1
v1
m1 m2
Кинетическая энергия, которая превратилась во внутреннюю:
m1v12 (m1 m2 ) v22
m1
EK
EK 1
2
2
m1 m2
Если масса покоящегося тела очень велика, то почти вся кинетическая
энергия превращается во внутреннюю. Слившееся тело почти покоится.
Если масса покоящегося тела очень мала, то не происходит заметного
превращения кинетической энергии во внутреннюю. Слившееся тело
движется практически с той же скоростью, с какой двигалось первое тело до
столкновения.

118.

11. Колебательное движение

119. Колебательный процесс

Колебаниями называются процессы, отличающиеся той или иной
степенью повторяемости.
В зависимости от физической природы повторяющегося процесса
различают колебания механические, электромагнитные и их
комбинации.
В зависимости от характера воздействия на колеблющуюся систему
различают:
• свободные (собственные) колебания;
• вынужденные колебания;
• автоколебания;
• параметрические колебания.

120. Колебательный процесс

Свободными (собственными) колебаниями называются колебания,
происходящие в системе, предоставленной самой себе после того, как
ей был сообщен толчок или она была выведена из положения
равновесия.
Вынужденными называются колебания, в процессе которых
колеблющаяся
система
подвергается
воздействию
внешней
периодически изменяющейся силы.
Автоколебания, как и вынужденные колебания, сопровождаются
воздействием на колеблющуюся систему внешних сил, однако моменты
времени, когда осуществляются эти воздействия, задаются самой
колеблющейся системой.
Параметрические колебания - это колебания, в процессе которых
происходит
периодическое
изменение
какого-либо
параметра системы.

121. Гармонические колебания

Гармоническими называются колебания, при которых колеблющаяся
величина (например, отклонение маятника) изменяется со временем по
закону синуса или косинуса.
x(t ) A sin( t 0 )
А – амплитуда колебаний, - частота колебаний, 0 – начальная
фаза колебаний
v(t ) x (t ) A cos( t 0 )
2
T
период колебаний
x 2 x 0
a(t ) x (t ) A 2 sin( t 0 ) 2 x(t )
Уравнение гармонических колебаний

122. Энергия гармонических колебаний

x(t ) A cos( t 0 )
mx 2 mA2 2 2
EK
sin ( t 0 )
2
2
kx 2 kA2
EП
cos2 ( t 0 )
2
2
kA2 mA2 2
E EK E П
2
2

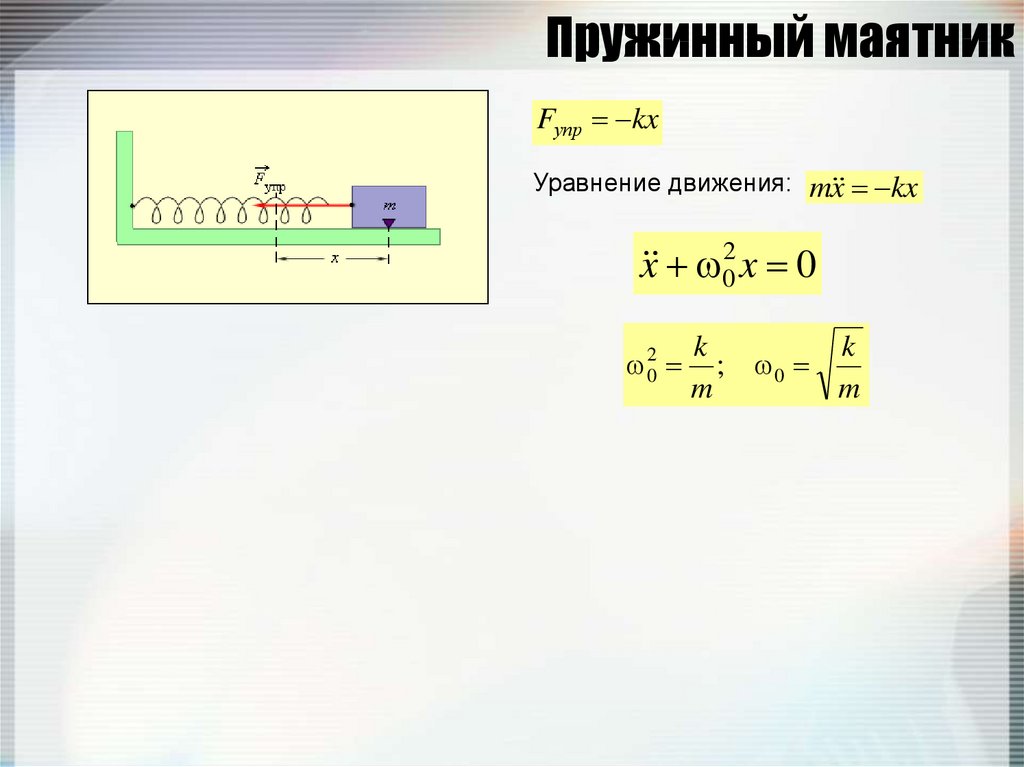
123. Пружинный маятник

Fупр kx
Уравнение движения: m x kx
x 02 x 0
02
k
k
; 0
m
m

124. Математический маятник

Математическим
маятником
называют
идеализированную систему, состоящую из
невесомой и нерастяжимой нити, на которой
подвешена масса, сосредоточенная в одной
точке (материальная точка), совершающая под
действием силы тяжести колебания вокруг
неподвижной точки или оси.
Вращательный момент сил:
M mgl sin
J ml 2 Уравнение моментов: ml 2
mgl sin
g
sin 0
l
Ограничимся малыми колебаниями: sin
g
02 ; 0
l
g
l
02
0
l
T 2
g

125. Физический маятник

Физическим маятником называют твердое тело, совершающее под
действием силы тяжести колебания вокруг неподвижной точки или оси.
Вращательный момент сил:
M mgd sin
d – расстояние между точкой подвеса и центром
масс маятника
Уравнение моментов:
mgd sin
J
Ограничимся малыми колебаниями: sin
2
mgd
mgd
2
0 0
0 ; 0
J
J
J
lпр
приведенная длина физического маятника
md
T 2
J
mgd
Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на
расстоянии приведенной длины от оси вращения, называется центром
качания физического маятника. При подвешивании маятника в точке
качания приведенная длина и период колебаний равны исходным. Точка
подвеса и центр качания обладают свойством взаимности.

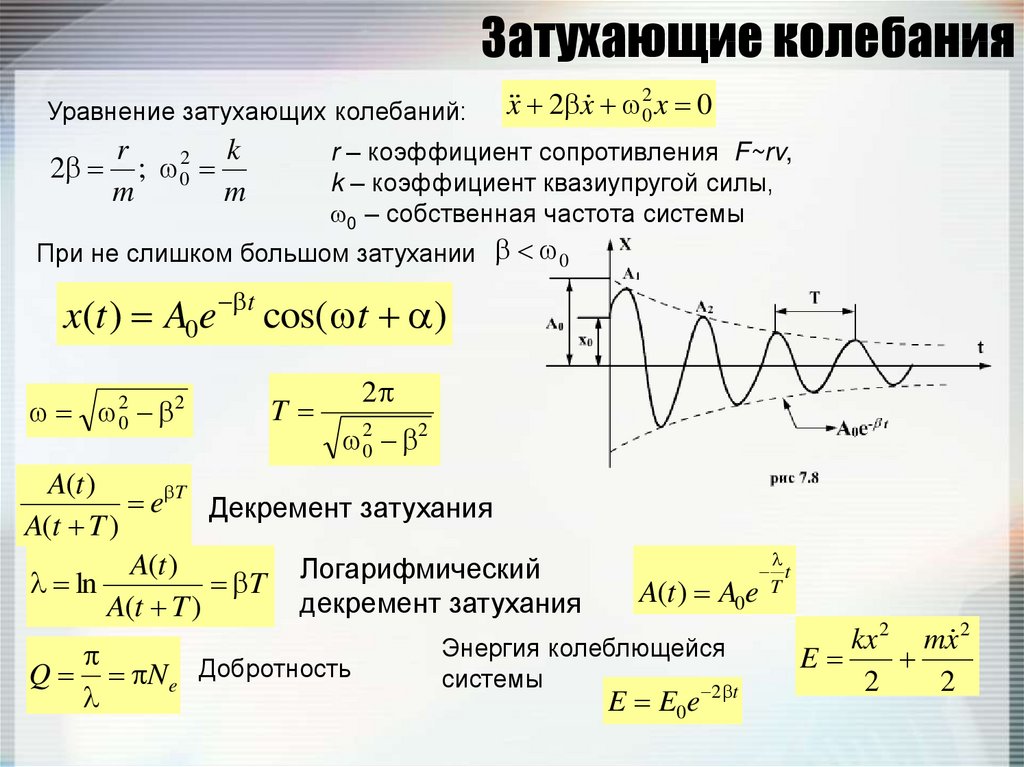
126. Затухающие колебания

Уравнение затухающих колебаний:
2
x 2 x 02 x 0
r – коэффициент сопротивления F~rv,
k – коэффициент квазиупругой силы,
0 – собственная частота системы
r
k
; 02
m
m
При не слишком большом затухании 0
x(t ) A0e t cos( t )
02
2
T
2
02 2
A(t )
e T Декремент затухания
A(t T )
A(t )
ln
T Логарифмический
декремент затухания
A(t T )
Q N e Добротность
A(t ) A0
Энергия колеблющейся
системы
2 t
E E0e
t
eT
kx 2 mx 2
E
2
2

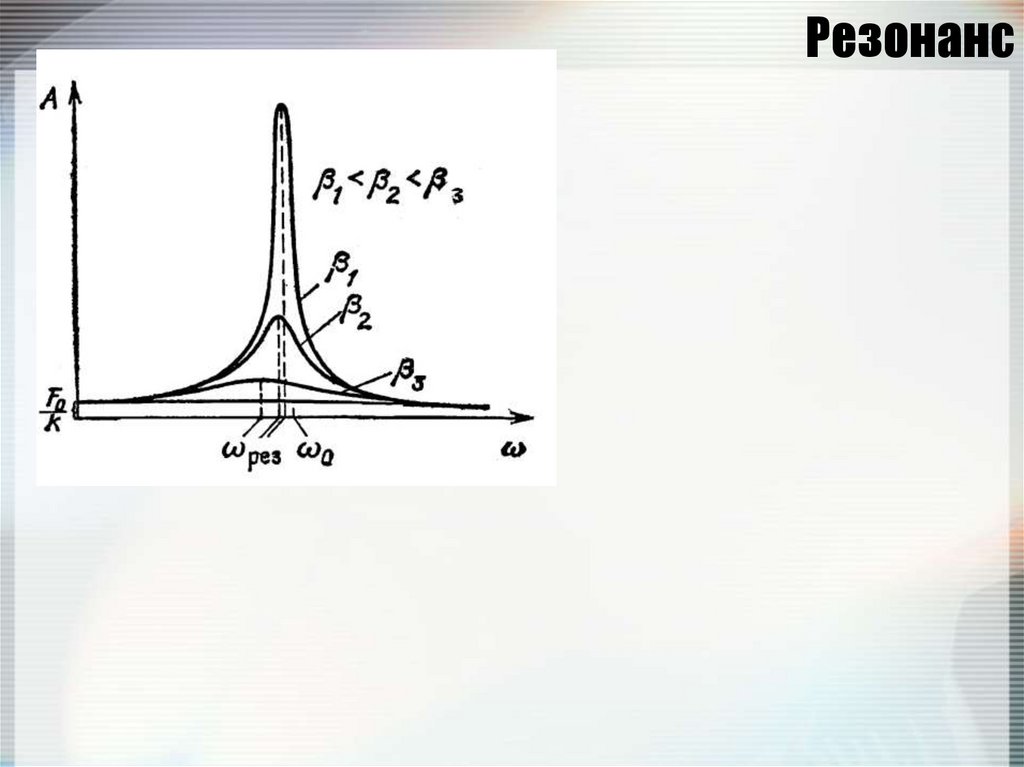
127. Вынужденные колебания

x 2 x 02 x f 0 cos t
2
x
cos t arctg 2
2
2
2 2
2 2
0
( 0 ) 4
f0 m

128. Резонанс

129.

12. Основы специальной
теории относительности

130. Постулаты Эйнштейна

Принцип относительности Эйнштейна
Все
законы
природы
одинаковы
инерциальных системах отсчета.
во
всех
Неизменность вида уравнения при замене в нем координат и времени от одной
системы отсчета к другой называется инвариантностью уравнения.
Другая формулировка принципа относительности:
Уравнения, выражающие законы природы, инвариантны по
отношению к преобразованию координат и времени от одной
инерциальной системы отсчета к другой.
Принцип постоянства скорости света
Скорость света в пустоте одинакова во всех
инерциальных системах отсчета и не зависит от
движения источников и приемников света.

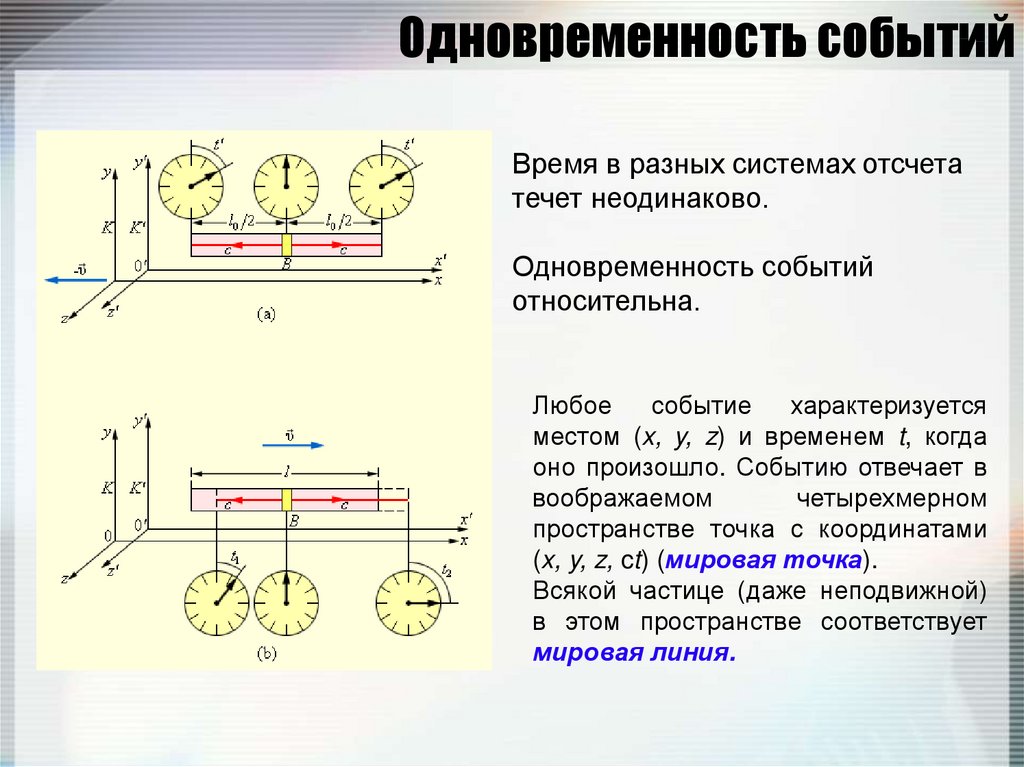
131. Одновременность событий

Время в разных системах отсчета
течет неодинаково.
Одновременность событий
относительна.
Любое
событие
характеризуется
местом (x, y, z) и временем t, когда
оно произошло. Событию отвечает в
воображаемом
четырехмерном
пространстве точка с координатами
(x, y, z, ct) (мировая точка).
Всякой частице (даже неподвижной)
в этом пространстве соответствует
мировая линия.

132. Преобразования Лоренца

Система К/ движется относительно системы К со скоростью v0. Оси Х и Х/ направлены вдоль v0.
xO ' v0t
xO/ v0t /
В общем случае преобразования
координат и времени от системы К/ к
системе К имеют вид:
x f1 ( x' , y' , z ' , t ' ) ;
y f 2 ( x' , y ' , z ' , t ' ) ;
z f 3 ( x' , y ' , z ' , t ' ) ; t f 4 ( x' , y ' , z ' , t ' )
Из однородности пространства и времени следует, что эти формулы должны быть
линейными:
x 1x' 2 y ' 3 z ' 4t ' 5 ,
где i константы.
dx 1dx' 2 d y ' 3 d z ' 4 d t '
f1
f
f
f
dx' 1 d y ' 1 d z ' 1 d t '
x'
y '
z '
t '

133. Преобразования Лоренца

Т.к. плоскости
совпадают, то
обращаться в
от значений
Поэтому:
{y=0 и y’=0} и {z=0 и z’=0} попарно
координаты, y и y’ (z и z’) должны
нуль одновременно и независимо
других координат и времени.
y y' , где const
В силу равноправности этих систем отсчета обратное соотношение то же:
y ' y
Перемножая оба соотношения, получаем:
2 1 1
Знак ( ) - сонаправленные оси, знак (-) - противоположно направленные оси.
У нас оси сонаправлены, поэтому:
y y'
z z'

134. Преобразования Лоренца

Начало координат 0 системы К имеет координату
x=0 в системе К и x’=-v0t’ в сиcтеме К’. Выражение
(x’+v0t’) должно обращаться в нуль одновременно
с координатой x. Тогда:
x ( x' v0t ' ), где const
Обратное рассмотрение дает:
x' ( x v0t )
Из равноправия систем следует, что коэффициент в обоих случаях должен
быть одинаковым. Найдем его из принципа постоянства скорости света.
Пусть в момент t=t’=0 в направлении Х (и Х’) посылается световой
импульс. Он регистрируется в точке х в момент t (в системе К) и в точке х’ в
момент t’ (в системе К’):
x ct , x' ct '
ct (ct ' v0t ' ) (c v0 )t '
2
2 2
2
c (c v 0 )
ct ' (ct v0t ) (c v0 )t
1
v02
1 2
c

135. Преобразования Лоренца

v0
c
t ' x'
x' ct '
c
x
; y y' ; z z' ; t
1 2
1 2
t x
x ct
c
x'
; y' y ; z' z ; t '
1 2
1 2

136. Следствия из преобразований Лоренца

Одновременность событий в разных системах отсчета
Пусть в системе К в точках с координатами x1 и x2 происходят одновременно
два события в момент времени t1 =t2 =b. Тогда этим событиям в системе К’
будут соответствовать моменты времени
b x1
c ;
t1/
1 2
b x2
c
t2/
1 2
Если события в системе К пространственно разобщены, то в
системе К’ они не будут одновременными.
В разных системах К’ этот временной промежуток (t ‘2 –t’1) различен
по величине и может различаться по знаку.
(Это относится лишь к событиям, между которыми отсутствует причинноследственная связь. Причинно связанные события ни в одной системе
отсчета не будут одновременными)

137. Следствия из преобразований Лоренца

Длина тел в разных системах отсчета
Рассмотрим стержень, расположенный вдоль оси x’ и покоящийся в
движущейся относительно неподвижной системы K со скорость v0 системе
отсчета K’. Его длина в системе К’ : l0 =x’2 – x’1 . Для определения его длины в
системе К нужно отметить координаты концов стержня x1 и x2 в один и тот же
момент времени b=t1 =t2
x1/
x1 v 0b
1 v 02 / c 2
x2/ x1/
, x2/
x2 v 0 b
1 v 02 / c 2
x2 x1
v2
l l0 1 2
c
1 v 02 / c 2
Длина стержня, измеренная в системе, относительно которой он движется
меньше длины, измеренной в системе отсчета, относительно которой он
покоится (собственной длины стержня).
Это
явление
называется
лоренцевым
(фитцджеральдовым)
сокращением.

138. Следствия из преобразований Лоренца

Промежуток времени между событиями
Пусть в одной и той же точке системы К’ a=x’1 =x’2 происходят два события в
моменты времени t’1 и t’2 .
t1
v0
v0
/
a
t
a
/
/
2
2
2
t
t
c , t
c t t 2 1
2
2
1
2
2
v0
v0
v02
1- 2
1- 2
1- 2
c
c
c
t1/
t
t /
v 02
1- 2
c
2
v
t / t 1 2
c
Время, отсчитанное по часам, движущимся вместе с телом, называется
собственным временем этого тела.
Собственное время всегда меньше, чем время, отсчитанное по часам,
движущимся относительно тела.

139. Интервал

s 2 c 2 t 2 x 2 y 2 z 2
s – интервал между событиями
l x 2 y 2 z 2 - расстояние между точками обычного трехмерного
пространства
s c 2 t 2 l 2
В системе К’ : s / 2 c 2 t / 2 x / 2 y / 2 z / 2
Из преобразований Лоренца следует:
t x
x c t
c
x'
; y ' y ; z ' z ; t '
1 2
1 2
s / 2 s 2
Интервал является инвариантом по отношению к переходу от одной
инерциальной системы отсчета к другой.

140. Интервал

Преобразуем формулу, связывающие промежутки времени между событиями
v2 1 2 2
1 2 2
2
t t 1 2
с t v t
с t l 2
с
с
c
/
1
s
c
Т.к. интервал является инвариантом по отношению к переходу от одной
инерциальной системы отсчета к другой, то и собственное время также
является инвариантом и не зависит, в какой системе отсчета наблюдается
данное явление.

141. Интервал

Интервал может быть :
вещественным
мнимым
нулевым
(c t l )
(c t l )
(c t l )
Нулевой интервал имеет место для событий, заключающихся в испускании
светового сигнала из точки ( x1 ; y1 ; z1) в момент t1 и приходе этого сигнала в
точку ( x2 ; y2 ; z2) в момент t2 .
События, разделенные вещественным интервалом, ни в одной системе
отсчета не могут стать одновременными. Вещественные интервалы
называются времениподобными.
События, разделенные мнимым интервалом, ни в одной системе отсчета не
могут оказаться пространственно совмещенными. Мнимые интервалы
называются пространственноподобными.
Причинно связанные события могут быть разделены лишь времениподобным
или нулевым интервалом.

142. Преобразование и сложение скоростей

Рассмотрим движение материальной точки.
dx
dy
dz
; v y ; vz
dt
dt
dt
dx'
dy'
dz'
v' x
; v' y
; v' z
dt
dt
dt
vx
Из преобразований Лоренца:
dx
dx' v0dt'
1
v02
c
2
в системе К
в системе К '
; dy dy'; dz dz'; dt
dt' ( v0 / c 2 )dx'
1 v02 c 2
Разделив первые три равенства на четвертое, получаем:
v /y 1 v02 c 2
v /z 1 v02 c 2
v /x v0
vx
; vy
; vz
/
2
/
2
1 v0 v x / c
1 v0 v x / c
1 v0 v /x / c 2
v y 1 v02 c 2
v z 1 v02 c 2
v x v0
v'x
; v' y
; v' z
2
2
1 v0 v x / c
1 v0 v x / c
1 v0 v x / c 2
При v0 << c эти соотношения переходят в формулы сложения скоростей
классической механики.

143. Релятивистское выражение для импульса

Уравнения Ньютона инвариантны по отношению к преобразованиям Галилея,
но не инвариантны по отношению к преобразованиям Лоренца.
Для замкнутой системы для релятивистских частиц закон сохранения
ньютоновского импульса не выполняется.
Альтернатива: или отказаться от ньютоновского определения импульса, или
от закона сохранения импульса.
p
mv
2
1
v
c2
- релятивистский импульс
mr
m – масса покоя (инвариантная масса)
mr – релятивистская масса (масса движения)
Основное уравнение релятивистской динамики:
dp
d mv
F
F
2
dt
dt
1 v2
c
m
v2
1 2
c

144. Релятивистское выражение для кинетической энергии

2-й закон Ньютона в виде ma=F в релятивистском случае неприменим, причем
сила и ускорение в общем случае неколлинеарны.
Определим кинетическую энергию как и в ньютоновской механике, как
величину, приращение которой равно работе действующей на частицу силы.
dEK Fvdt
Fdt d (mr v) dmr v mr dv
vdv v dv
dE K v(dmr v mr dv) v 2 dmr mr vdv
dEK c 2dmr
mr2c 2 mr2 v 2 m2c 2
2mr c 2dmr 2mr v 2dmr 2mr2 vdv
EK (mr m)c 2
1
Релятивистская кинетическая энергия частицы EK mc
2
1
2
1

145. Полная энергия и энергия покоя

dp
F
Воспользуемся уравнением релятивистской динамики:
dt
mv
d
v
dt 1 v 2 / c 2
Умножим на v :
Fv
d mv
F
2
dt
1 v2
c
Дифференцируем левую часть:
mv
d
v
dt 1 v 2 / c 2
d v2
1
dv
2
3/ 2
2
2
dt c
dt
1 v / c
1 2 d v 2 v 2 dv 1
m
m
d v 2 2 v 2 2
2 1 2 v
2 v 1 2 c
v
3/ 2
2
2 3/ 2 2
2
2
dt c c dt 2 1 v / c
dt c
1 v / c
c
v
1
mv
2 1 v 2 / c 2
1
mc2
2 1 v2 / c 2
mc2
1 v / c
2
2
3/ 2
d v2 d
mc2
2
dt c dt 1 v 2 / c 2
E
mc2
d
2
2
1 v / c
Fdr
Полная энергия тела (без учета потенциальной энергии
внешних воздействий)

146. Полная энергия и энергия покоя

Когда тело покоится, то
E0 mc 2
- энергия покоя
E EK E0 mc
1 mc2
1 2
2
1
E c p 2 mc2
Если p mc , то
E mc2
E
p 2 v
c
2
2
2
1
p
p
p
2
2
1
mc 1
mc
2m
mc
2 mc
2
E
2
2 2
p
m
c inv
2
c