Similar presentations:
Вращательное движение твердого тела
1. Механика 2
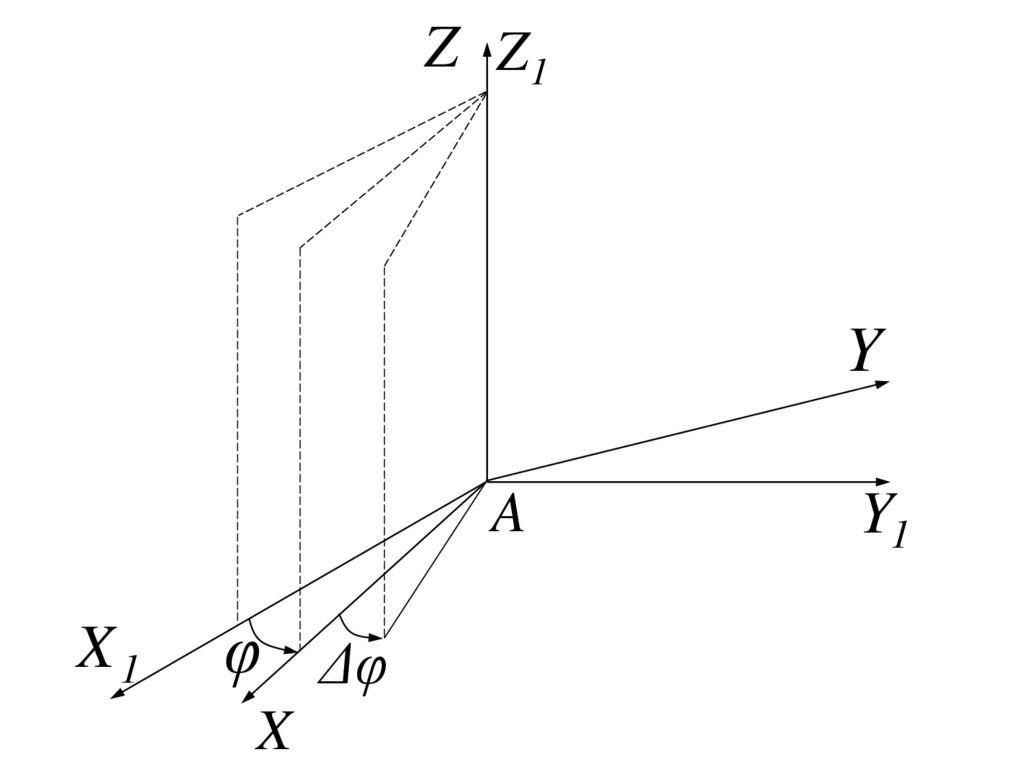
2. Вращательное движение твердого тела
• Вращательное движение твердого тела – этотакое движение при котором какие-нибудь
две точки остаются неподвижными.
• Проходящая через эти точки прямая
называется осью вращения.
3.
Z Z1Y
A
X1
φ Δφ
X
Y1
4. Вращательное движение твердого тела
Δφ = φ ( t + Δt ) - φ ( t )(ωz )ср
Δφ
=
Δt
средняя угловая скорость
Δφ dφ
ωz = lim
=
=φ
dt
Δt →0 Δt
угловая скорость
5. Вектор угловой скорости и ускорения
dω
k z k
dt
Вектор угловой скорости- это вектор численно равный первой производной по
времени от закона изменения угла поворота, направленный по оси вращения в
ту сторону, чтобы глядя с конца вектора угловой скорости вращение происходило
бы против часовой стрелки.
dω d z
ε
k zk
dt
dt
Вектор углового ускорения- это вектор численно равный первой
производной по времени угловой скорости,
6. Скорость точки тела, вращающегося вокруг неподвижной оси
Рассмотрим векторное произведение для скорости, еслиначало координат лежит на оси вращения
v [ , r ]
i
Формула Эйлера
j k
v [ , r ] x y z
x
y
z
7.
Вектор угловой скорости и ускорениеv [ , r ]
Определение скорости, через вектор
угловой скорости
d
a
[ , r ]
dt
d
a [
, r ] [ , v ]
dt
Ускорение
[ A,[ B, C ]] B( A, C ) C ( A, B)
a [ε , r ] [ ,[ , r ]]
a [ε , r ] ( r ) r ( )
a * ( r ) n * ( 2 r )
если r
r r
8. Первый закон Ньютона
Существуют такие инерциальные системыотсчёта, относительно
которых материальные точки, когда на них
не действуют силы (или действие сил
уравновешено), находятся в состоянии
покоя или
равномерного прямолинейного движения.
9. Понятие силы
• Сила причина движения (Аристотель)• Сила причина ускорения (Галилей)
Сила — это векторная величина, являющаяся мерой механического
воздействия на тело со стороны других тел или полей, в результате
которого тело приобретает ускорение или изменяет свою форму и
размеры.
[H ] [L / T 2M ]
10. Классики механики
Аристотель 382-322 д.н.эGalileo Galilei 1562-1642
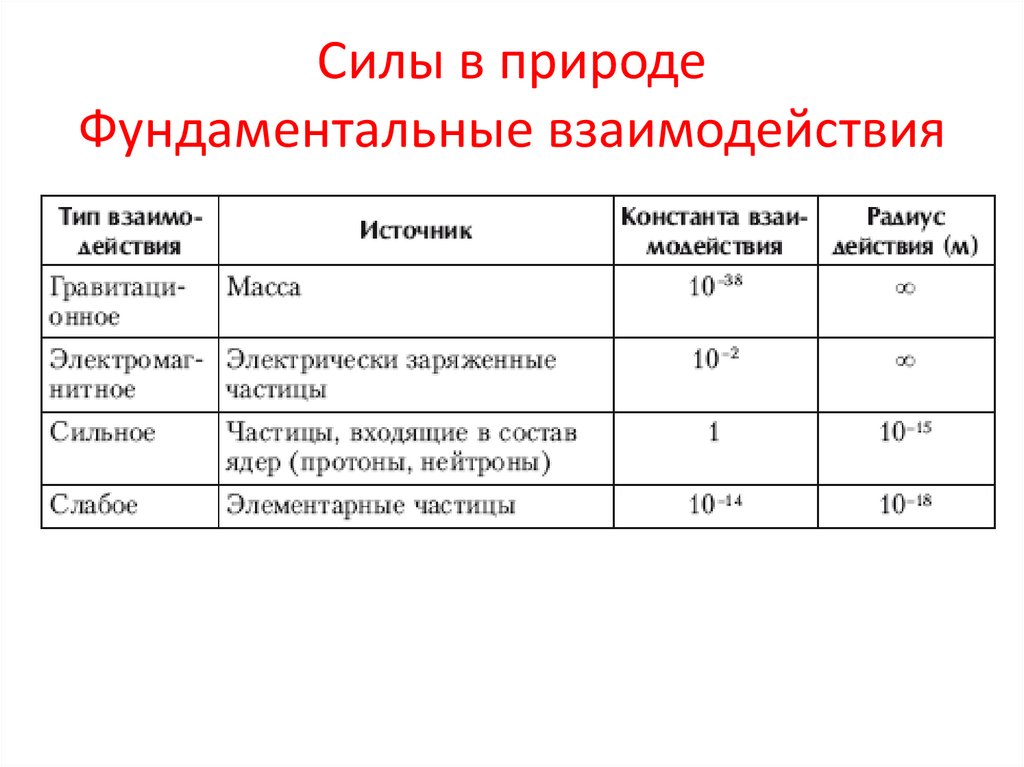
11. Силы в природе Фундаментальные взаимодействия
12. Неинерциальность систем отсчета
Ускорения из-за вращения земли вокруг осисут
an Rземля сут 2 ~ 0.032 m / c 2
2
2
7.3*10 5 с 1
T
24*3600
Ускорения из-за вращения земли вокруг солнца
Rземля 6500км
an Rорб год 2
Rорб 150 млн.км
Ускорения из вращения нашей галактики
0.000001 m / c 2
~ 0.0055 m / c 2
13. Понятие группы Галилея
Набор преобразований какого-либо множества называется группой,если вместе с любыми двумя преобразованиями он содержит результат
их последовательного применения, а вместе с каждым
преобразованием — обратное преобразование.
Преобразование Галилея будет:
r r ut
t t'
r
- радиус вектор в неподвижной инерциальной системе отсчета (ИСО).
r
- радиус вектор в движущейся ИСО.
u
- скорость движущейся ИСО
14. Второй закон Ньютона
В инерциальных системах отсчёта ускорение материальнойточки прямо пропорционально действующей на нее силе,
совпадает с ней по направлению и обратно пропорционально
ее массе.
F
a
m
d 2 r F (r , v , t )
2
dt
m
F (r , r , t )
r
m
-дифференциальное уравнение 2-ого порядка,
-уравнение движения материальной точки .
15. Масса
Масса тела — физическая величина, являющаяся одной из основныххарактеристик материи, определяющая ее инерционные (инертная масса) и
гравитационные (гравитационная масса) свойства.
Обобщенный закон Галилея -
g
Fgr
mgr
min
min
[кг ] [ M ]
Friedrich Bessel
1784 -1846
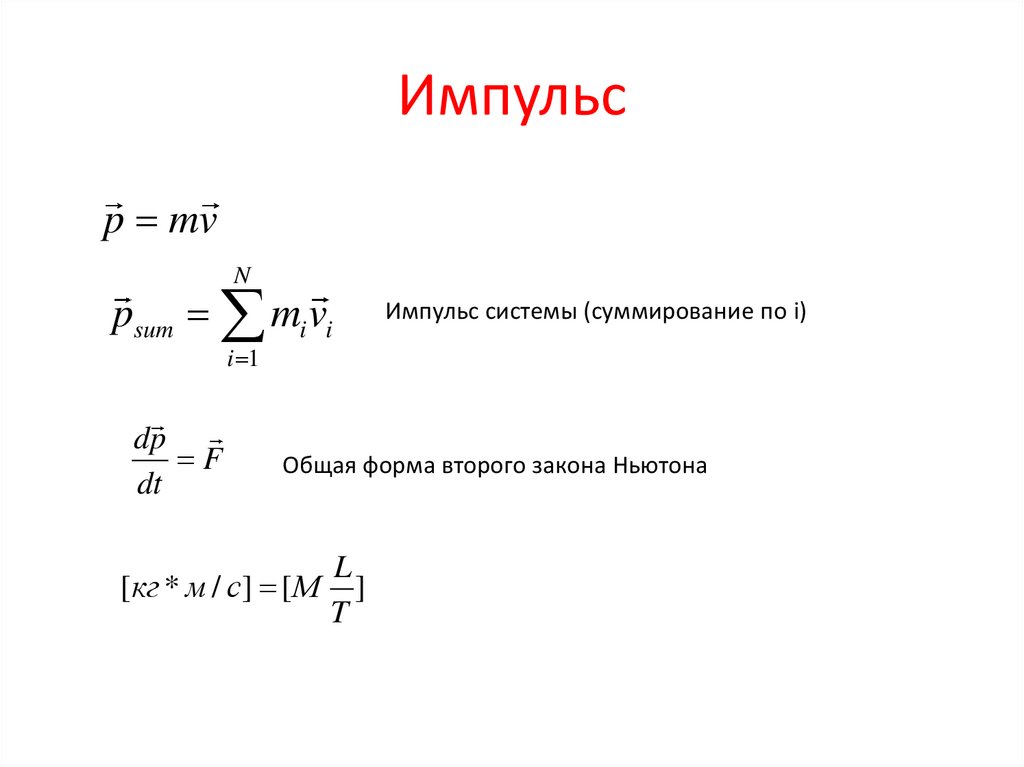
16. Импульс
p mvN
psum mi vi
Импульс системы (суммирование по i)
i 1
dp
F
dt
Общая форма второго закона Ньютона
[кг * м / c] [ M
L
]
T
17. Третий закон Ньютона
Силы , которые действуют между материальными точками равныпо модулю, противоположны по направлению
и параллельны прямой, которая их соединяет.
F12 F21
18. Закон сохранения импульса
Для системы из двух материальных точек
dp1
F12 f1
dt
dp2
F21 f 2
dt
F12 сила, действующая на материальную точку 1 со стороны точки 2
F21 сила, действующая на материальную точку 2 со стороны точки 1
f1 и f1
- внешние силы
dp1 dp2
f1 f 2
dt
dt
F12 F21
f1 f 2 0
d
dp1 dp2
( p1 p2 ) 0
0
dt
dt
dt
p1 p2 pconst
19. Закон сохранения импульса
Для системы из N материальных точек
dp1
F12 F13 ...F1N f1
dt
dp2
F21 F22 ...F2 N f1
dt
......
dpN
FN 1 FN 2 ...FNN 1 f N
dt
Fij Fji
N
N
dpi
fi
i 1 dt
i 1
N
f1 f 2 ... f N 0
dpi
0
i 1 dt
N
p
i 1
i
const
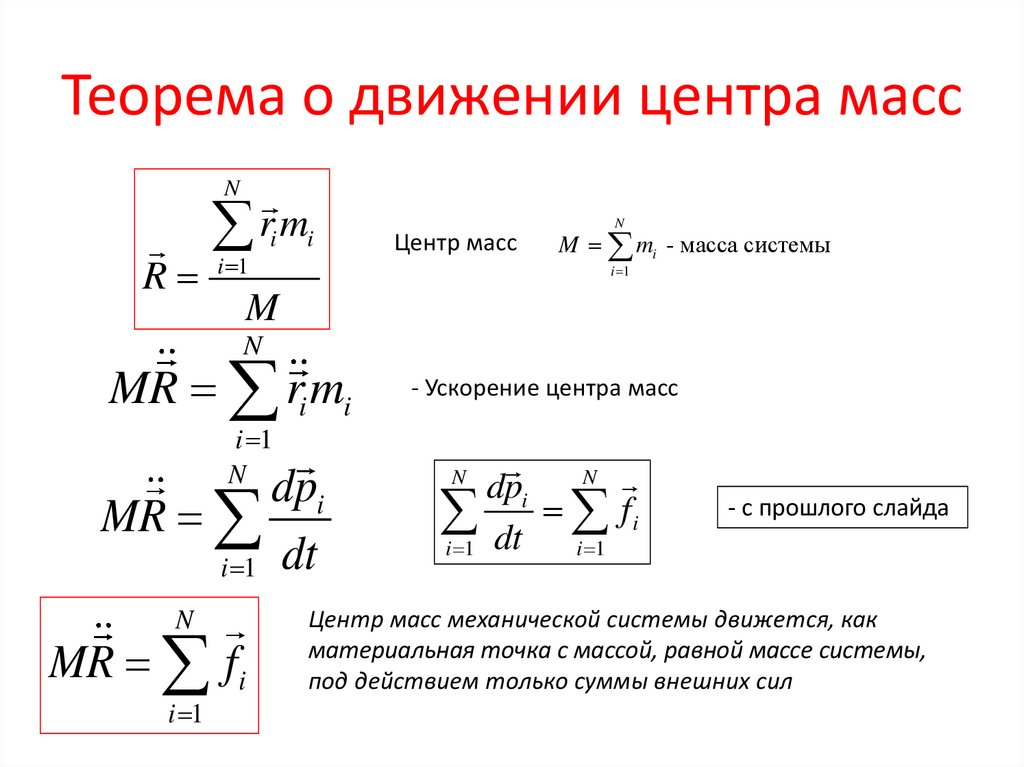
20. Теорема о движении центра масс
NR
rm
i 1
i
i
Центр масс
N
M mi - масса системы
i 1
M
N
MR ri mi
i 1
N
dpi
MR
i 1 dt
N
MR fi
i 1
- Ускорение центра масс
N
N
dpi
fi
i 1 dt
i 1
- с прошлого слайда
Центр масс механической системы движется, как
материальная точка с массой, равной массе системы,
под действием только суммы внешних сил
21.
Механическая работаdr ds
dA ( F dr ) F ds cos Fs ds
22. Работа силы и кинетическая энергия материальной точки
Скалярное произведение силы на перемещение:dA ( F dr )
Пусть сила действует на материальную точку,
найдем дифференциал работы:
dv
dr
mv 2
dA F dr m dr m dv mvdv d
dK
dt
dt
2
Кинетическая энергия материальной точки называется:
mv 2
K dK
2
23. Кинетическая энергия системы материальных точек
Одной материальной точки:mv 2
K
2
mi vi 2
K
2
i 1
N
Системы N материальных точек:
24. Столкновения
Абсолютно упругий удар — столкновение двух тел, врезультате которого полная кинетическая энергия
сохраняется.
Центральный удар, когда тела после удара движутся по
прямой, проходящей через их центры масс.
Абсолютно неупругий удар — столкновение двух тел, в
результате которого тела приобретают одинаковую
скорость (движутся, как единое целое).
25. Примеры
Упругое центральное столкновение:m1v1 m2 v2 m1u1 m2u2
ЗСИ
m1v12 m2 v2 2 m1u12 m2u2 2
2
2
2
2
ЗСЭ
m1 (v1 u1 ) m2 (u2 v2 )
m1 / m2 (v1 u1 ) (u2 v2 )
u1
(2v2 v1 )m2 m1v1
(m1 m2 )
(2v1 v2 )m1 m2 v2
u2
(m1 m2 )
m1 (v12 u12 ) m2 (u2 2 v2 2 )
ЗСП
ЗСЭ
(v1 u1 ) (u2 v2 )
Случай равных масс:
m1 m2
u1 v2
u2 v1
Случай столкновения с
движущейся стенкой:
m2
u1 2v2 v1
u2 v2
p 2v2 2v1 m1
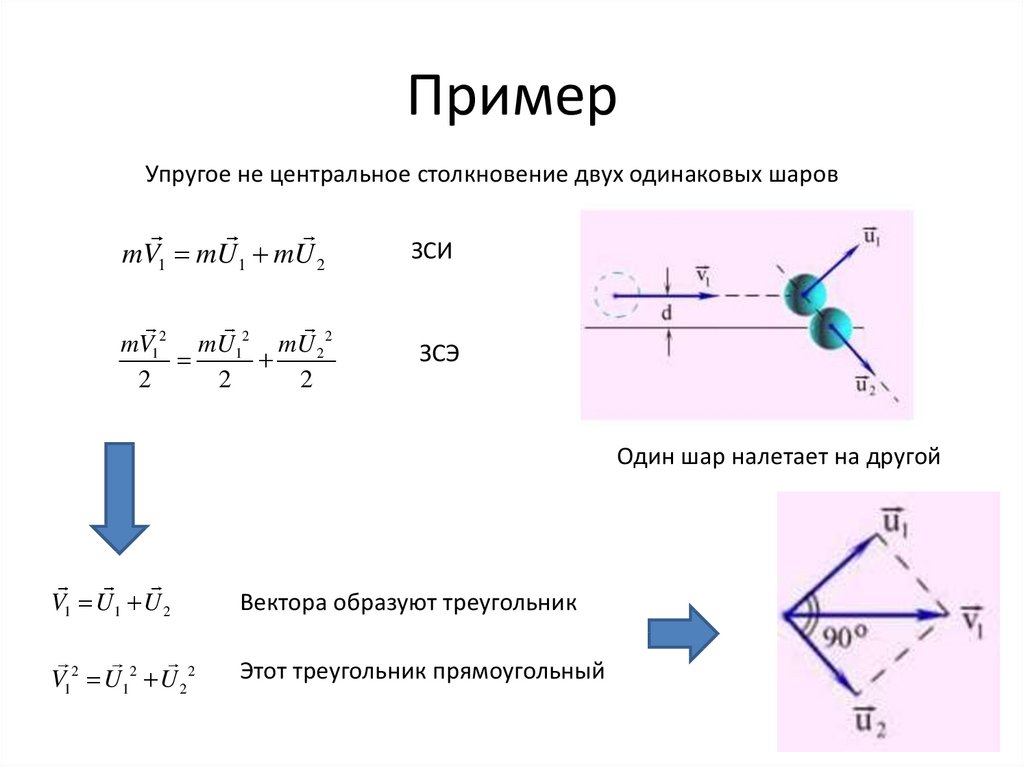
26. Пример
Упругое не центральное столкновение двух одинаковых шаровmV1 mU1 mU 2
ЗСИ
mV12 mU12 mU 2 2
2
2
2
ЗСЭ
Один шар налетает на другой
V1 U1 U 2
Вектора образуют треугольник
V12 U12 U 2 2
Этот треугольник прямоугольный
27. Кинетическая энергия системы материальных точек
Одной материальной точки:mv 2
K
2
mi vi 2
K
2
i 1
N
Системы N материальных точек:
28. Теорема Кёнига
Nmi vi 2
mi vi '2 MvM 2
K
2
2
2
i 1
i 1
N
vi vi ' vM
vM
- скорость движения центра масс
vi '
- скорость точки i в системе центра масс
N
M mi
- полная масса
i 1
N
mi vi 2
mi (vi ' vM ) 2
K
2
2
i 1
i 1
N
N
mi vi '2 N mi vM 2
(vM mi vi ') N mi vi '2 MvM 2
K
2
2
2
2
2
2
i 1
i 1
i 1
i 1
N
N
(vM mi vi ')
2
(vM mi vi ') 0
2
i 1
i 1
N
Johann König
1712 - 1757
29.
МощностьМощность – скалярная величина, равная работе
силы, совершаемой за единицу времени;
(характеризует скорость, с которой совершается
работа) .
[N] = Дж/c = Вт (СИ)
dA Fdr
N
F
dt
dt
1 л.с. = 735 Вт
Средняя мощность работы постоянной силы:
N ( F ср )
30.
Консервативные силыСтационарное поле – поле
постоянным со временем.
сил,
остающееся
Консервативные силы – силы, работа которых не
зависит от формы пути, по которому перемещается
тело, а определяется только начальным или
конечным
положением
тела
1
и
2.
Потенциальное поле – поле, в котором действуют
консервативные силы.
Работа консервативных сил на замкнутом контуре
равна нулю.
A12a = A12b; 12a = - A21a;
Aзамкн = 0
31. Центральные силы
Центральные силы – силы, зависящие только отрасстояния между взаимодействующими частицами
и направленные вдоль прямой, соединяющей эти
частицы (гравитационные, кулоновские, упругие).
Все центральные силы являются консервативными!
Т.е. работа центральных сил не зависит от формы
пути, по которому перемещается тело.
32.
Потенциальная энергия2
2
A Fdr Fs ds
1
1
Так как работа консервативных сил зависит только от
начального и конечного положений тела, то
существует скалярная функция, определяющая
положение тел, убыль которой равна работе.
A U1 U 2 U
U – потенциальная энергия.
14
33.
ЭнергияЭнергияскалярная
физическая
характеризующая способность тел
работу.
Кинетическая энергия
- энергия механического
движения тела.
12
величина,
совершать
Потенциальная энергия
– энергия, зависящая от
положения
тела
в
потенциальном поле
сил.



























 physics
physics








