Similar presentations:
Динамика материальной точки и поступательного движения твердого тела
1.
2. Динамика материальной точки и поступательного движения твердого тела
Первый закон Ньютона (законом инерции ):всякая материальная точка (тело) сохраняет состояние покоя
или равномерного прямолинейного движения до тех пор, пока
воздействие со стороны других тел не заставит ее изменить
это состояние.
Первый закон Ньютона утверждает существование
инерциальных систем отсчета.
Первый закон Ньютона выполняется в инерциальных
системах отсчета.
Стремление тела сохранять состояние покоя или
равномерного прямолинейного движения называется
инертностью.
3.
Масса тела — физическая величина, определяющая ееинерционные (инертная масса) и гравитационные
(гравитационная масса) свойства.
Сила — это векторная величина, являющаяся мерой
механического воздействия на тело со стороны других тел
или полей, в результате которого тело приобретает
ускорение или изменяет свою форму и размеры.
Второй закон Ньютона: ускорение, приобретаемое
материальной точкой (телом), пропорционально
вызывающей его силе, совпадает с нею по направлению и
обратно пропорционально массе материальной точки
(тела).
dv
F ma m .
dt
d
F (mv ) .
dt
P mv ,
4. Уравнение движения материальной точки
В механике большое значение имеетпринцип независимости действия сил:
если на материальную точку действует одновременно
несколько сил, то каждая из этих сил сообщает
материальной точке ускорение согласно второму закону
Ньютона, как будто других сил не было.
dP
F .
dt
5. Принцип независимости действия сил
• Если на материальную точку действует одновременнонесколько сил, то каждая из этих сил сообщает
материальной точке ускорение согласно второму
закону Ньютона, как будто других сил не было.
aτ
Fτ
a dv / dt
a
an v / R
F
2
v R
an
Fn
2
dv
mv
2
F ma m ; Fn man
m R.
dt
R
6. Третий закон Ньютона
• Силы, с которыми действуют друг на другаматериальные точки, всегда равны по модулю,
противоположно направлены и действуют вдоль
прямой, соединяющей эти точки.
Сила, действующая на
первую материальную точку
Сила, действующая на
вторую материальную точку
со стороны второй
со стороны первой
F12
F12 F21
F21
7. Силы трения
Различают внешнее (сухое) и внутреннее (жидкое иливязкое) трение.
Внешним трением называется трение, возникающее в
плоскости касания двух соприкасающихся тел при их
относительном перемещении. Если соприкасающиеся тела
неподвижны друг относительно друга, говорят о трении
покоя, если же происходит относительное перемещение
этих тел, то в зависимости от характера их относительного
движения говорят о трении скольжения, качения или
верчения.
Внутренним трением называется трение между частями
одного и того же тела, например между различными слоями
жидкости или газа, скорости которых меняются от слоя к
слою.
8.
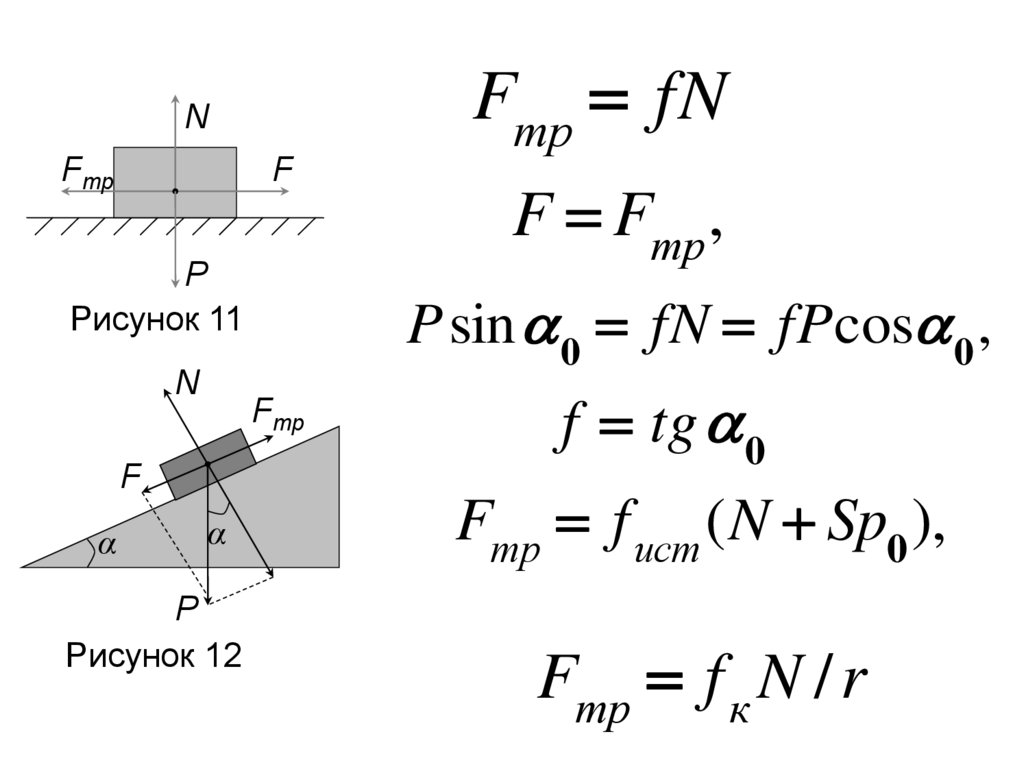
Fтр fNN
Fтр
F
P
Рисунок 11
N
α
P sin 0 fN fPcos 0 ,
Fтр
F
α
P
Рисунок 12
F Fтр ,
f tg 0
Fтр f ист ( N Sp0 ),
Fтр f к N / r
9. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой
• Силы взаимодействия между материальнымиточками механической системы называются
внутренними.
• Силы, с которыми на материальные точки системы
действуют внешние тела, называются внешними.
• Механическая система тел, на которую не
действуют внешние силы, называется замкнутой
(или изолированной).
10. Рассмотрим механическую систему, состоящую из многих тел
/ //
F1 , F2 ,..., Fn
F1 , F2 ,..., Fn
• равнодействующие внутренних
сил, действующих на каждое из
этих тел
• равнодействующие внешних
сил действующих на каждое из
этих тел
m1 , m2 ,..., mn
• массы
v1 , v2 ,..., vn
• скорости тел системы
и
11. закон Ньютона для каждого из тел механической системы
d(m1v1 ) F1/ F1 ,
dt
d (m v ) F / F ,
2
2
dt 2 2
………………………………,
d
(mnvn ) Fn/ Fn.
dt
12. Складывая почленно эти уравнения, получим
d(m1v1 m2v2 ... mnvn ) F1/ F2/ ... Fn/ F1 F2 ... Fn.
dt
d
(m1v1 m2v2 ... mnvn ) F1 F2 ... Fn.
dt
dP
F1 F2 ... Fn.
dt
n
P mi v i
i 1
13. Закон сохранения импульса (для замкнутой системы)
• Закон сохранения импульса – фундаментальный законприроды. Он справедлив не только в классической физике,
но и в квантовой механике.
• Закон сохранения импульса является следствием
однородности пространства.
• Однородность пространства заключается в том, что при
параллельном переносе в пространстве замкнутой системы
тел как целого ее физические свойства и законы движения
не изменяются, т.е. не зависят от выбора положения начала
координат инерциальной системы отсчета.
dP n d
(mi vi ) 0 ,
dt i 1 dt
n
P mi vi const.
i 1
14. Центр масс (или центр инерции) механической системы
• - это воображаемая точка С, положение которойхарактеризует распределение массы этой системы.
Её радиус-вектор равен:
mi ri
n
n
m mi
i 1
rC
,
m
dri
mi
dt
i 1
n
drC
vC
dt
m
i 1
Pi mi vi
mi vi
n
i 1
m
.
P mvC ,
15. Закон движения центра масс
• Центр масс замкнутой системы, либодвижется прямолинейно и равномерно,
либо остается неподвижным.
dvC
m
F1 F2 ... Fn ,
dt
16. Уравнение движения тела переменной массы
• Изменение импульса системы за отрезок времени dtdP m dm v dv dm v u mv ,
dP mdv u dm 0
dv
dm
m u
,
dt
dt
dm
v u
u ln m C .
m
dm
u
называют реактивной силой
dt
17.
m0Если в начальный момент времени скорость ракеты
равна нулю, а ее стартовая масса m0 то
C u ln m0 .
Следовательно,
v u ln (m0 / m) - формула Циолковского
из которой следует:
1) чем больше конечная масса ракеты т, тем больше
должна быть стартовая масса ракеты;
2) чем больше скорость истечения и газов, тем больше
может быть конечная масса при данной стартовой
массе ракеты.

















 physics
physics








