Динамика материальной точки и поступательного движения твёрдого тела

1. Динамика материальной точки и поступательного движения твёрдого тела

Динамика - это раздел физики, изучающий движение тел с
учётом взаимодействия этих тел с другими телами
Любая механическая задача может быть решена лишь в определенной
системе отсчета. Простейшая система – инерциальная. Абсолютно
инерциальная система – абстракция. Все реальные системы могут
считаться инерциальными лишь приближенно.
Законы Ньютона
Первый закон Ньютона (закон инерции)
Существуют
такие
системы
отсчёта,
называемые
инерциальными, относительно которых материальная точка при
отсутствии внешних воздействий сохраняет величину и
направление своей скорости неограниченно долго.
Или по-другому: скорость любого тела остаётся постоянной пока
воздействие других тел не вызовет её изменение.
1

2.

Важным свойством инерциальных систем является их
инвариантность. Уравнения динамики не изменяются при
переходе от одной инерциальной системы к другой.
Сила F –
общая
мера
различных
взаимодействия между телами.
видов
Инертность - свойство, благодаря которому тела
по разному изменяют состояние своего движения
под действием одинаковой силы
Масса m – мера инертности тела
Импульс p m – мера движения тела
2

3.

Второй закон Ньютона (основной закон динамики)
Быстрота изменения импульса материальной точки равна
действующей на неё силе.
dp
F
dt
dp F dt
Произведение Fdt – называется импульсом силы.
Изменение импульса материальной точки равно импульсу
силы.
p m В классической механике m = const.
dp d m
d
m
m a
dt
dt
dt
m a F
Ускорение, сообщаемое материальной точке силой, прямо
пропорционально силе и обратно пропорционально массе этой
точки
3

4.

Второй закон Ньютона. Произведение массы тела на его
ускорение равно действующей на тело силе
2
m
d r
dt
F
2
- это дифференциальное уравнение второго
порядка. Для его решения необходимо
интегрирование. Для интегрирования
необходимо знание величины F.
С физической точки зрения сила различна в зависимости от ее
природы. С математической: сила – функция, зависящая от
dr
координат, времени и скорости F t , r ,
dt
4

5.

Основные виды сил
m F12 r12 M
Гравитационные
В случае M > m, r=const,
Сила сухого трения
F
M
M
r
r2
g
m
mg
2
F N
Сила упругости
F kx
Сила кулоновская
F qE
F q , B
Сила Лоренца
mM r12
F12 2
r12 r12
5

6.

Третий закон Ньютона.
Силы взаимодействия 2-х материальных точек равны по
величине, противоположны по направлению и имеют общую
линию действия.
F12 – сила, которую испытывает 1-ое
тело со стороны 2-го.
F12 F21
F21 – сила, которую испытывает 2-ое
тело со стороны 1-го.
Третий закон верен в любой системе отсчёта.
Сложение сил. Принцип независимости сил.
Если на материальную точку действуют несколько сил, то
каждая из них сообщает точке такое ускорение, как если бы
других сил не было.
F Fi
i
Fi
F
a
ai
m
i m
i
(ai – ускорение под действием силы Fi)
6

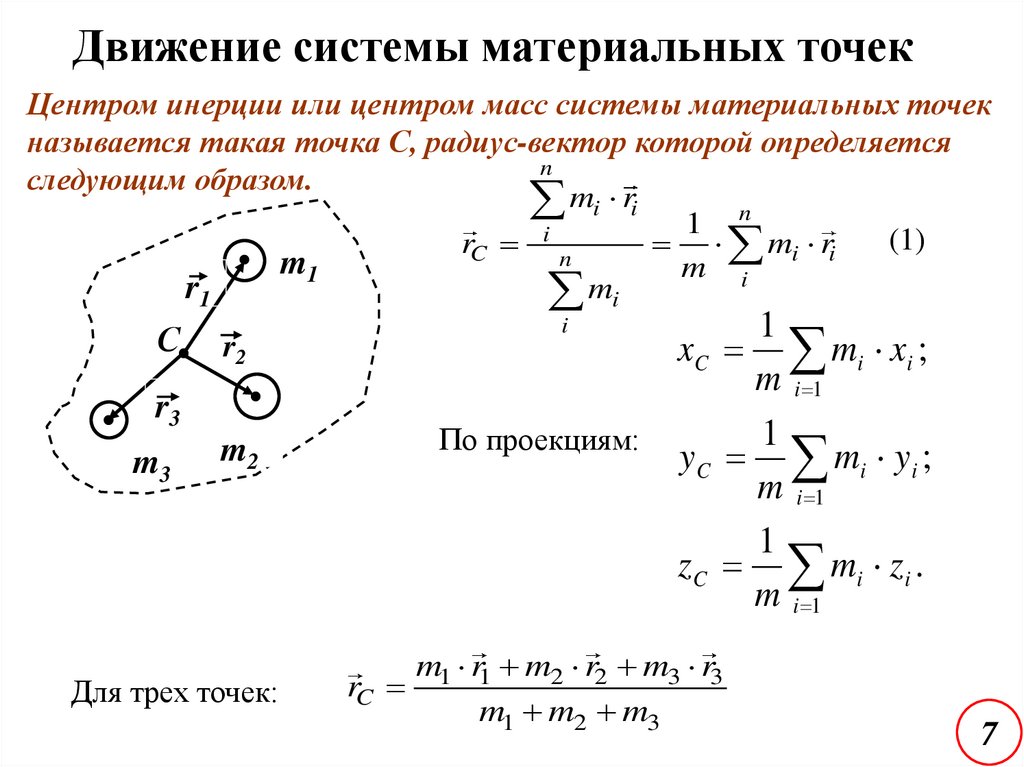
7.

Движение системы материальных точек
Центром инерции или центром масс системы материальных точек
называется такая точка С, радиус-вектор которой определяется
n
следующим образом.
mi ri 1 n
(1)
mi ri
rC i n
m1
m i
r1
mi
С
r2
r3
m3
m2
Для трех точек:
1
x C mi x i ;
m i 1
1
По проекциям:
y C mi y i ;
m i 1
1
z C mi z i .
m i 1
i
m1 r1 m2 r2 m3 r3
rC
m1 m2 m3
7

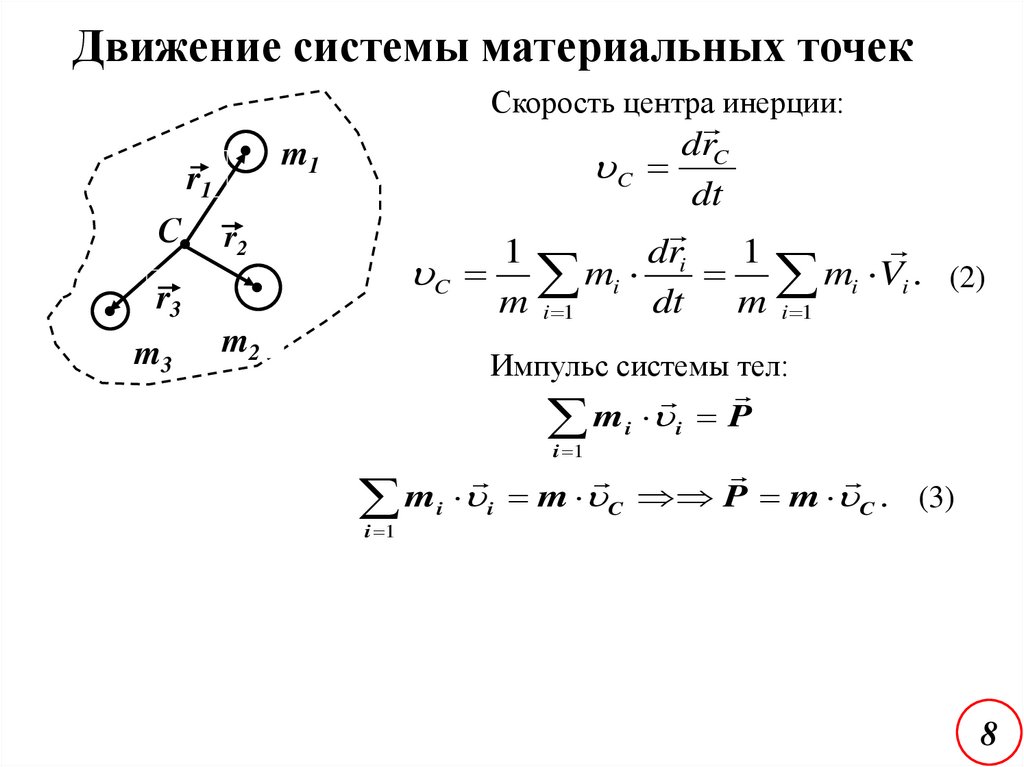
8.

Движение системы материальных точек
Скорость центра инерции:
m1
r1
С
drC
C
dt
dri
1
1
C mi
mi Vi . (2)
m i 1
dt
m i 1
r2
r3
m3
m2
Импульс системы тел:
m i i P
i 1
mi i m C P m C . (3)
i 1
8

9.

Движение системы материальных точек
Тела,
не
входящие
в
состав
рассматриваемой системы, называются
внешними
телами,
а
силы,
действующие со стороны внешних тел,
называются внешними силами.
Силы взаимодействия между телами
внутри
системы
называются
внутренними силами.:
Результирующая всех внутренних сил,
действующих на i – тое тело:
Fi
Fik Fi1 Fi 2 Fin .
n
k 1; k i
Индекс k пробегает все значения кроме k = i, поскольку i – тое тело
не может действовать само на себя.:
9

10.

Движение системы материальных точек
Для каждой точки системы можно записать уравнения по
второму закону Ньютона.
Вн
d
m1 V! F1 F12 F13 F1n ;
dt
Вн
d
m 2 V 2 F2 F21 F23 F2 n ;
dt
Вн
d
m n V n Fn Fn1 Fn 2 Fn , n 1 .
dt
10

11.

Движение системы материальных точек
Сложив уравнения системы получим:
n Вн
d
i 1 dt mi Vi i 1 Fi F12 F21 F13 F31 Fn 1,n Fn,n 1 .
0
n
n
d
Вн
m
V
F
i
i
i .
i 1 dt
i 1
n
Дифференцируем левую часть:
d
d
dP
m
V
m
V
.
Р – импульс системы
i
i
i
i
dt
dt
i 1 dt
i 1
F – главный вектор всех
dP
F.
внешних сил
dt
n
n
Т.к.
P m C .
аС – ускорение центра
d
m C F или m aC F . инерции системы
dt
11

12.

Движение системы материальных точек
Центр инерции механической системы тел
движется как материальная точка, масса
которой равна массе всей системы и на
которую действует сила, равная главному
вектору внешних сил приложенных к системе.
m aC F
12

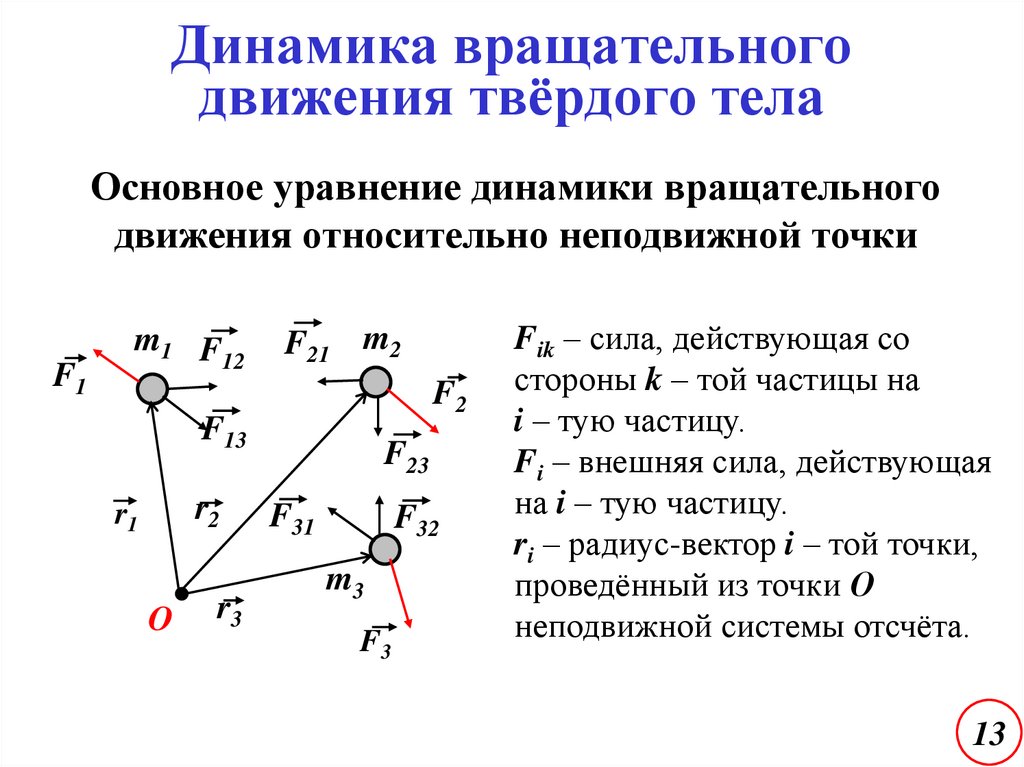
13.

Динамика вращательного
движения твёрдого тела
Основное уравнение динамики вращательного
движения относительно неподвижной точки
F1
m1 F
12
F21 m2
F2
F13
r2
r1
O
r3
F23
F31
F32
m3
F3
Fik – сила, действующая со
стороны k – той частицы на
i – тую частицу.
Fi – внешняя сила, действующая
на i – тую частицу.
ri – радиус-вектор i – той точки,
проведённый из точки О
неподвижной системы отсчёта.
13

14.

уравнение динамики для первой частицы
d
m1 1 F12 F13 F1 × r1
dt
Уравнение умножим векторно на вектор r1
d
(*)
r
,
m
1 dt 1 1 r1, F12 r1, F13 r1, F1
Вынесем знак производной за знак векторного произведения в (*),
для этого рассмотрим выражение:
d
dr1
d
r
,
m
,
m
r
,
m
1 1
1 1 1
1 1 1
dt
dt
dt
Векторное произведение
двух коллинеарных
векторов
14

15.

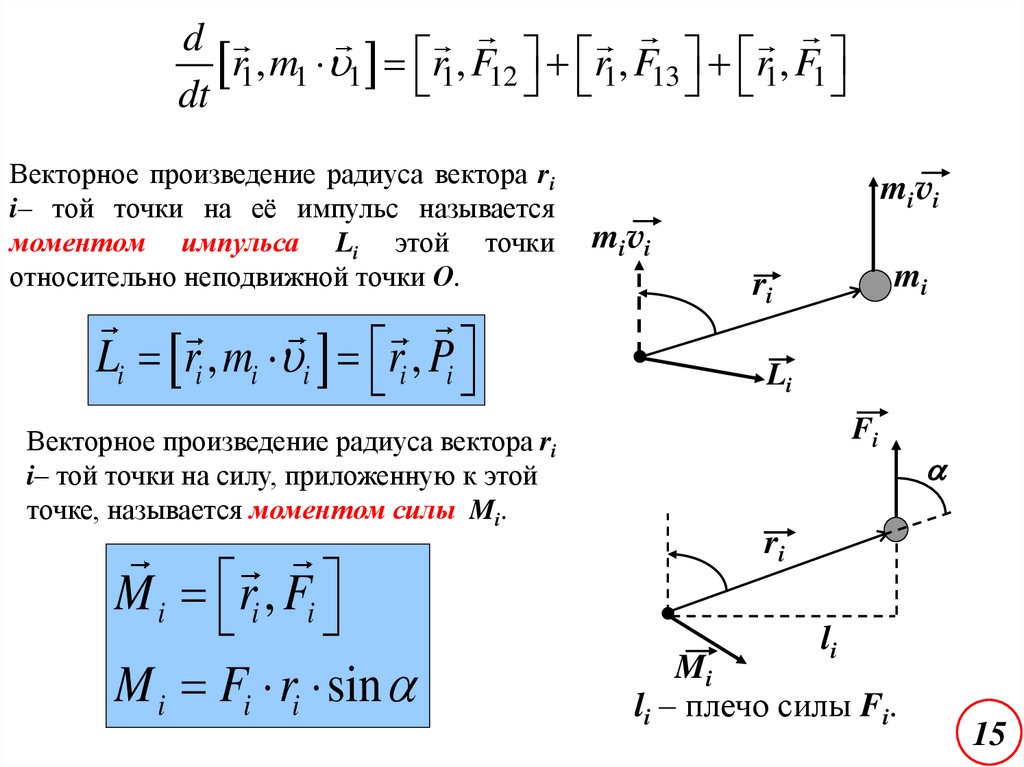
d
r1, m1 1 r1, F12 r1, F13 r1, F1
dt
Векторное произведение радиуса вектора ri
i– той точки на её импульс называется
моментом импульса Li этой точки
относительно неподвижной точки О.
Li ri , mi i ri , Pi
Векторное произведение радиуса вектора ri
i– той точки на силу, приложенную к этой
точке, называется моментом силы Mi.
M i ri , Fi
M i Fi ri sin
mivi
mivi
mi
ri
Li
Fi
ri
li
Mi
li – плечо силы Fi.
15

16.

В итоге получаем уравнение динамики для трех частиц:
dL1
M 12 M 13 M 1 ;
dt
dL2
M 21 M 23 M 2 ;
dt
dL3
M 31 M 32 M 3.
dt
Просуммируем правую и левую части уравнений:
d
L1 L2 L3 M 1 M 2 M 3 .
dt
N
M 0 т.к F F .
ik
ik
ki
i ,k
16

17.

N
Обозначим
M M
i
i
N
и
L L
i
i
L – момент импульса твёрдого тела. М – суммарный момент
внешних сил.
dL
M
dt
Закон динамики вращательного движения твёрдого тела
для случая вращения относительно неподвижной точки.
17

18.

Уравнение динамики вращательного движения
относительно неподвижной оси
Из равенства векторов следует равенство их
проекций на любое направление.
dL
M
dt
dLz
Mz
dt
z
Lz
Ri
O'
bi
O
vi
ri bi Ri
Liz ri , mi i bi , mi i Ri , mi i
ri
Этот вектор перпендикулярен оси z, и
его проекция на эту ось равна нулю.
18

19.

Liz Ri , mi i
Liz mi Ri i mi R , т.к. R
2
i
N
N
N
Lz Liz mi R mi R J z
i 1
i 1
2
i
i 1
2
i
Jz – момент инерции тела относительно оси (его еще
обозначают I).
m
N
J z mi Ri2
i 1
точнее
J z R 2 dm
0
(R – расстояние от dm до оси z)
19

20.

d Lz d
J z M z
dt
dt
Для твёрдого тела Jz = const.
Твердое тело - это совокупность материальных точек (частиц),
расстояние между которыми не меняется со временем.
d
Jz
M z или J z M z
dt
J M
Это основное уравнение динамики
вращательного движения
относительно неподвижной оси
J – Момент инерции (аналог массы для
поступательного движения).
20

21.

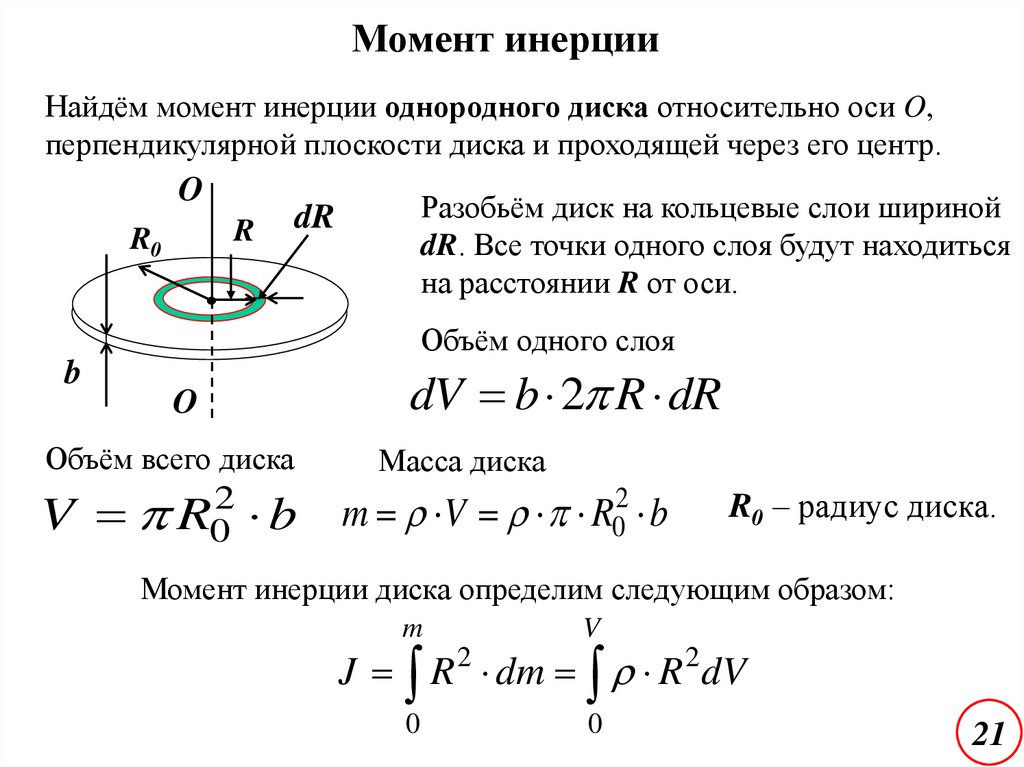
Момент инерции
Найдём момент инерции однородного диска относительно оси O,
перпендикулярной плоскости диска и проходящей через его центр.
O
R
R0
Разобьём диск на кольцевые слои шириной
dR. Все точки одного слоя будут находиться
на расстоянии R от оси.
dR
Объём одного слоя
b
O
Объём всего диска
2
V R0 b
dV b 2 R dR
Масса диска
m V R02 b
R0 – радиус диска.
Момент инерции диска определим следующим образом:
m
V
J R dm R dV
2
0
2
0
21

22.

dV
R0
R0
J 0 R b 2 R dR 2 b R dR
2
3
0
4
R0
2 b
O
4
dR
2
R0 b
O'
R
b
O
0
m
O'
2
R0
2
2
mR0 Для однородного
2
диска
Если бы мы хотели найти момент
инерции диска относительно оси O'
(см. рисунок), то вычисления были бы
значительно сложнее. В таких случаях
нахождение момента инерции
облегчается, если воспользоваться
теоремой Штейнера
22

23.

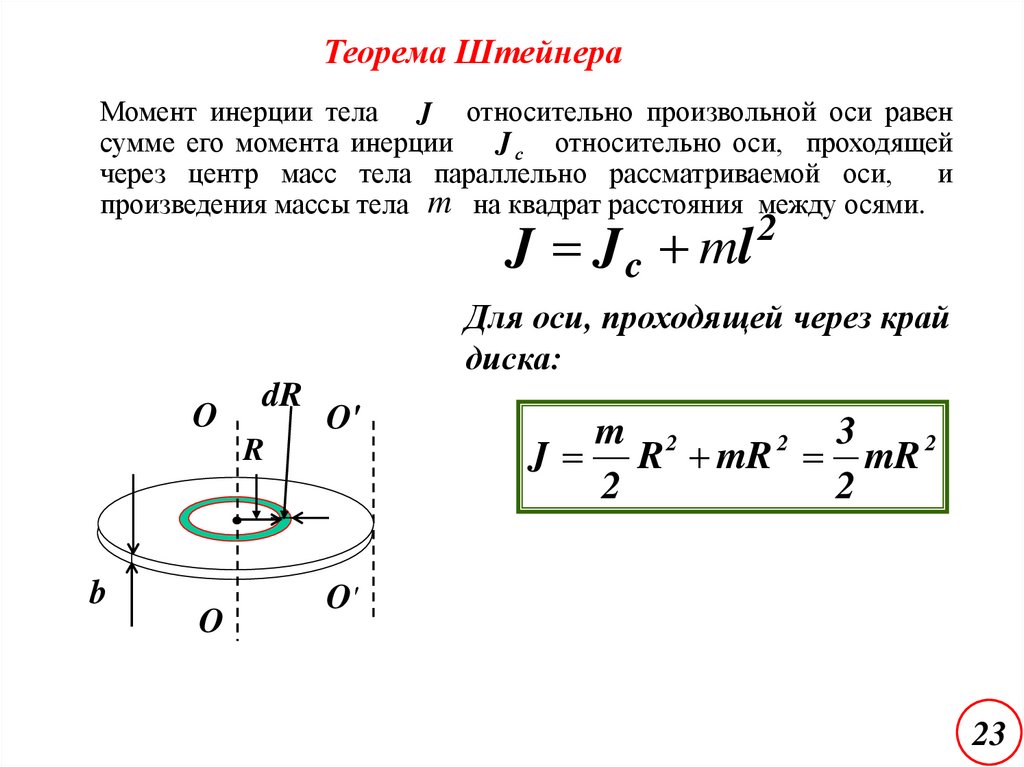
Теорема Штейнера
Момент инерции тела J относительно произвольной оси равен
сумме его момента инерции J с относительно оси, проходящей
через центр масс тела параллельно рассматриваемой оси,
и
произведения массы тела m на квадрат расстояния между осями.
J J c ml
2
Для оси, проходящей через край
диска:
O
dR
O'
R
b
O
m 2
3
2
J R mR mR 2
2
2
O'
23

24.

Момент инерции тонкого однородного стержня относительно
оси, перпендикулярной к стержню и проходящей через его
середину
O
l
O
b
(b << l)
1
2
J0
ml .
12
Для диска или цилиндра при любом отношении радиуса к
длине момент инерции относительно оси, совпадающей с
геометрической осью цилиндра
R
O
O
l
1
2
J 0 mR .
2
24

25.

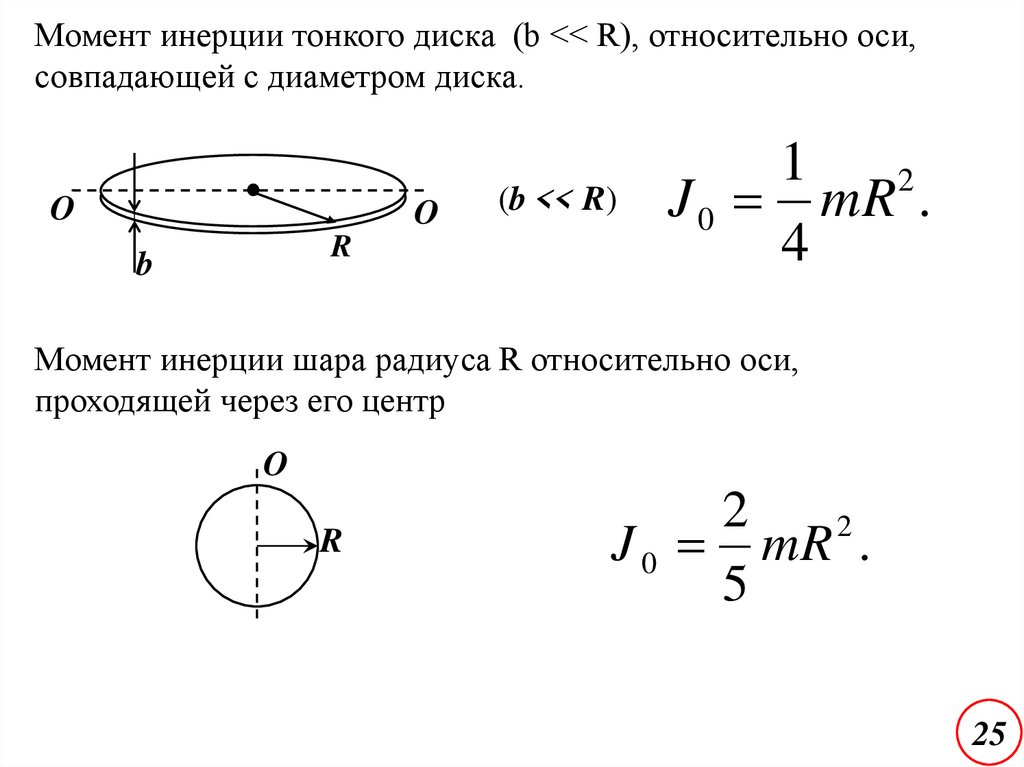
Момент инерции тонкого диска (b << R), относительно оси,
совпадающей с диаметром диска.
O
O
R
b
(b << R)
1
2
J 0 mR .
4
Момент инерции шара радиуса R относительно оси,
проходящей через его центр
O
R
2
2
J 0 mR .
5
25

26.

Формулы для вычисления моментов инерции для стандартных тел
26