Similar presentations:
Динамика материальной точки и поступательного движения твердого тела
1. Динамика материальной точки и поступательного движения твердого тела
Лекция №32. План лекции
• 1. Инерциальные системы отсчета. Сила, масса иимпульс тела. Первый закон Ньютона.
• 2. Второй закон Ньютона.
• 3. Третий закон Ньютона.
• 4. Силы в механике.
• 5. Центр масс. Закон сохранения импульса.
• 6. Реактивное движение. Уравнение Мещерского.
Формула Циолковского.
3. 1. Инерциальные системы отсчета. Сила, масса и импульс тела. Первый закон Ньютона
4.
Динамикаизучает
механическое
взаимодействие тел с учетом вызвавших его
причин.
Динамику интересуют силы, действующие на
тела.
5.
Сила –FВФВ, характеризующая механическое взаимодействиетел и полей.
кг м
F 1 2 1 Н (ньютон)
с
О действии сил можно судить по двум признакам:
1) Появление ускорения (динамическое действие)
2) Деформация тел (статическое действие)
Принцип суперпозиции для сил:
Если на тело действуют несколько сил, то силы действуют
независимо друг от друга, и результат их действия
складывается по правилам действия над векторами.
n
F Fi F1 F2 ... Fn
i 1
6.
Инерциальная система отсчета (ИСО) – это системаотсчета, связанная со свободным невращающимся
телом.
Свободным называется тело, не взаимодействующее с
другими телами.
В основе классической механики лежат три
закона, сформулированные И. Ньютоном в
книге «Математических началах
натуральной философии» (1687 г.).
Классическая механика – это механика
Ньютона.
Сэр Исаак (Айзек)
Ньютон
1642-1727
7. Первый закон Ньютона (закон инерции)
Первый закон Ньютона говорит о движении свободной м.т.относительно ИСО.
Формулировки :
Ньютон:
«Всякое тело продолжает удерживаться в состоянии покоя или равномерного
и прямолинейного движения, пока и поскольку оно не понуждается
приложенными силами изменить это состояние»
А.К. Кикоин, И.К. Кикоин, Физика-10:
«Существуют такие системы отсчета, относительно которых поступательно
движущееся тело сохраняет свою скорость постоянной, если на него не
действуют другие тела (или действия других тел компенсируются)»
Мы:
В ИСО свободная м.т. либо покоится либо
движется равномерно и прямолинейно.
8.
Инерция – явление сохранения скорости тела по модулю инаправлению до тех пор, пока на него не подействуют другие тела.
Инертность – свойство тел, проявляющееся в том, что скорость тела
изменяется не мгновенно, а с течением времени.
Масса тела m – СФВ, являющаяся мерой инертных свойств тела при его
поступательном движении и мерой гравитационных свойств тела.
[m] = 1 кг
p (количество движения) м.т. – ВФВ, являющаяся мерой ее
Импульс
механического движения и равная произведению массы м.т. на вектор
ее скорости:
p m
9. 2. Второй закон Ньютона (основной закон динамики)
Второй закон Ньютона отвечает на вопрос, какизменяется механическое движение материальной
точки (тела) под действием приложенных к ней сил.
10.
• Ускорение, приобретаемое м.т. В ИСО, прямо пропорционально силе,действующей на нее, и обратно пропорционально ее массе:
F
a
m
d
a
dt
d F
dt m
dp
F
dt
(1)
d m
F
dt
(2)
• Скорость изменения импульса тела равна равнодействующей всех сил,
приложенных к телу (более общая формулировка 2-го закона Ньютона).
Выражение (1) не выполняется в тех случаях, когда масса тела изменяется.
Выражение (2) является универсальным.
11.
3. Третий закон Ньютона12. 3. Третий закон Ньютона
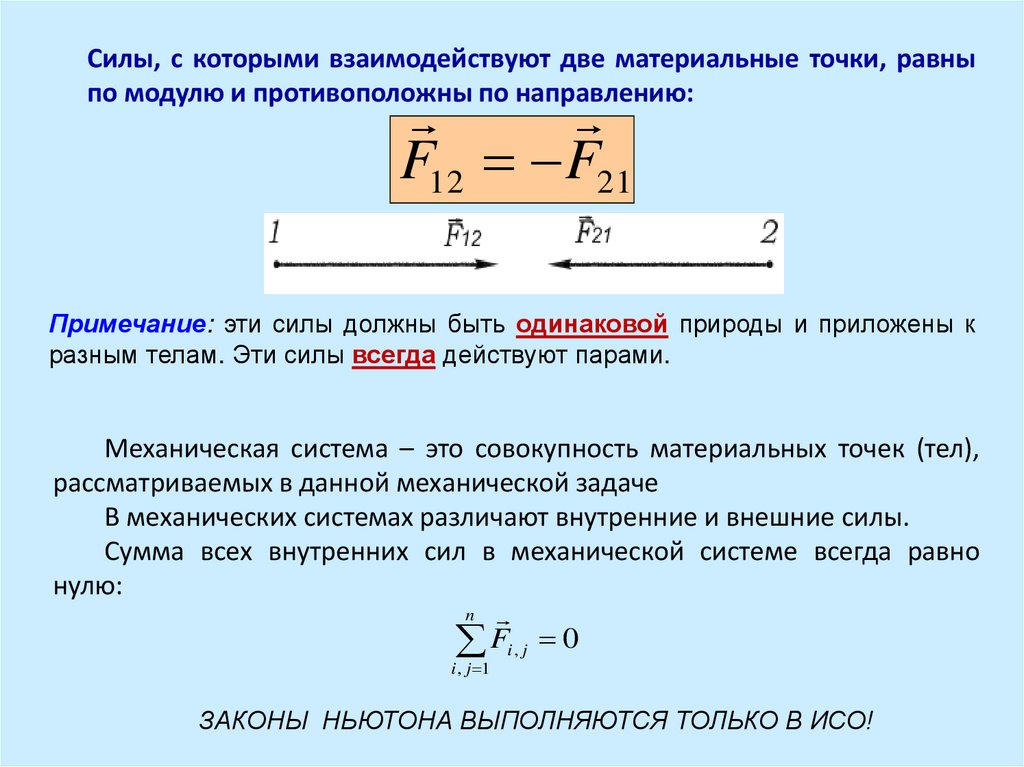
Силы, с которыми взаимодействуют две материальные точки, равныпо модулю и противоположны по направлению:
F12 F21
Примечание: эти силы должны быть одинаковой природы и приложены к
разным телам. Эти силы всегда действуют парами.
Механическая система – это совокупность материальных точек (тел),
рассматриваемых в данной механической задаче
В механических системах различают внутренние и внешние силы.
Сумма всех внутренних сил в механической системе всегда равно
нулю:
n
Fi , j 0
i , j 1
ЗАКОНЫ НЬЮТОНА ВЫПОЛНЯЮТСЯ ТОЛЬКО В ИСО!
13.
4. Силы в механикеА. Упругие силы;
Б. Силы трения;
В. Гравитационные силы;
Г. Вес тела. Сила реакции опоры.
14. 4. Силы в механике
• В современной физике различают четыре видавзаимодействий:
• 1)
гравитационное
(взаимодействие
обусловленное
всемирным тяготением);
• 2) электромагнитное (осуществляемое через электрическиие
и магнитные поля);
• 3) Сильное или ядерное (обеспечивающее связь частиц в
атомном ядре);
• 4) слабое (ответственное за многие процессы распада
элементарных частиц).
В рамках классической механики имеют дело с гравитационными и
электромагнитными силами, а также с силами упругости и трения, вес
тела, силой реакцией опоры.
15.
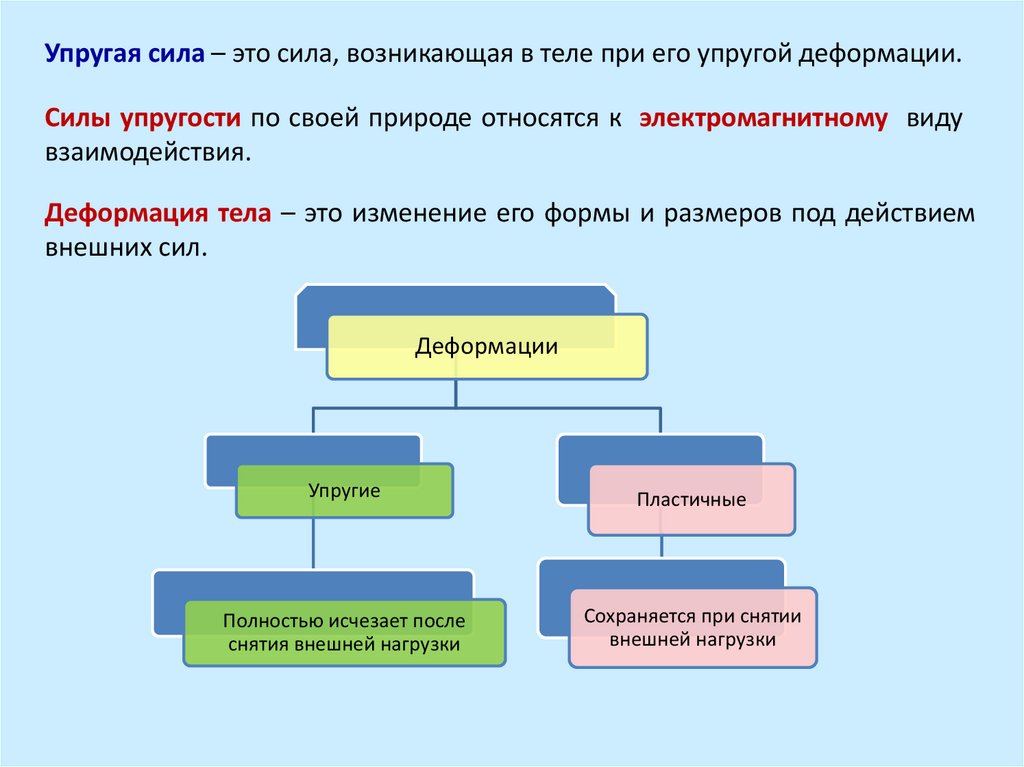
А. Упругие силы16.
Упругая сила – это сила, возникающая в теле при его упругой деформации.Силы упругости по своей природе относятся к электромагнитному виду
взаимодействия.
Деформация тела – это изменение его формы и размеров под действием
внешних сил.
Деформации
Упругие
Пластичные
Полностью исчезает после
снятия внешней нагрузки
Сохраняется при снятии
внешней нагрузки
17. А. Упругие силы
Закон Гука:Сила Fу упругости, возникающая в
пропорциональна удлинению l тела.
теле,
Fу k l kx
Fу x k l kx
x = l = l – l0 - абсолютное удлинение тела
k - коэффициент упругости (жесткость) тела
Роберт Гук
(1635-1703)
Виды деформаций
Растяжение и сжатие
Кручение
Сдвиг
Изгиб
18.
pFвнеш.n
S
- механическое усилие
[ ] = [p] = 1 Н/м2 = 1 Па (паскаль)
В случае упругих деформаций однородных тел:
= p, т.к. Fу = Fвнеш
Закон Гука: Механическое напряжение, возникающее в теле, прямо
пропорционально его относительному удлинению (сжатию):
E
[E] = 1 Н/м2 = 1 Па
E - модуль Юнга
Физический смысл модуля Юнга:
E = , если
1
l l l0
l0
l0
l – l0 = l0
l = 2l0
Модуль Юнга равен такому нормальному механическому напряжению, возникающему
в теле, при котором относительное удлинение было бы равно единице, следовательно,
приращение длины было бы равно первоначальной длине стержня, т.е. оно изменило
свои размеры в два раза.
19.
Б. Силы трения• Силы трения возникают (проявляются) при
перемещении соприкасающихся тел или их частей
друг относительно друга.
• Трение – взаимодействие между соприкасающимися
телами, препятствующее их относительному
движению.
• Сила трения относится к электромагнитному виду
взаимодействия.
20. Деформация растяжения (сжатия)
Трение возникающее при относительном перемещении двух соприкасающихся
тел, называют внешним трением, а трение между частями одного и того же
сплошного тела (например жидкости или газа) называют внутренним трением.
Внешнее (сухое) трение – трение между поверхностями твердых тел.
Внутренне (вязкое) трение – трение между движущимися слоями жидкости или
газа.
Внешнее трение:
1. Трение покоя;
2. Трение скольжения;
3. Трение качения.
Fтр. п F
Fтр. п - сила трения покоя.
[ п] = 1
Fтр.п.max = пN
п - коэффициент трения покоя
21.
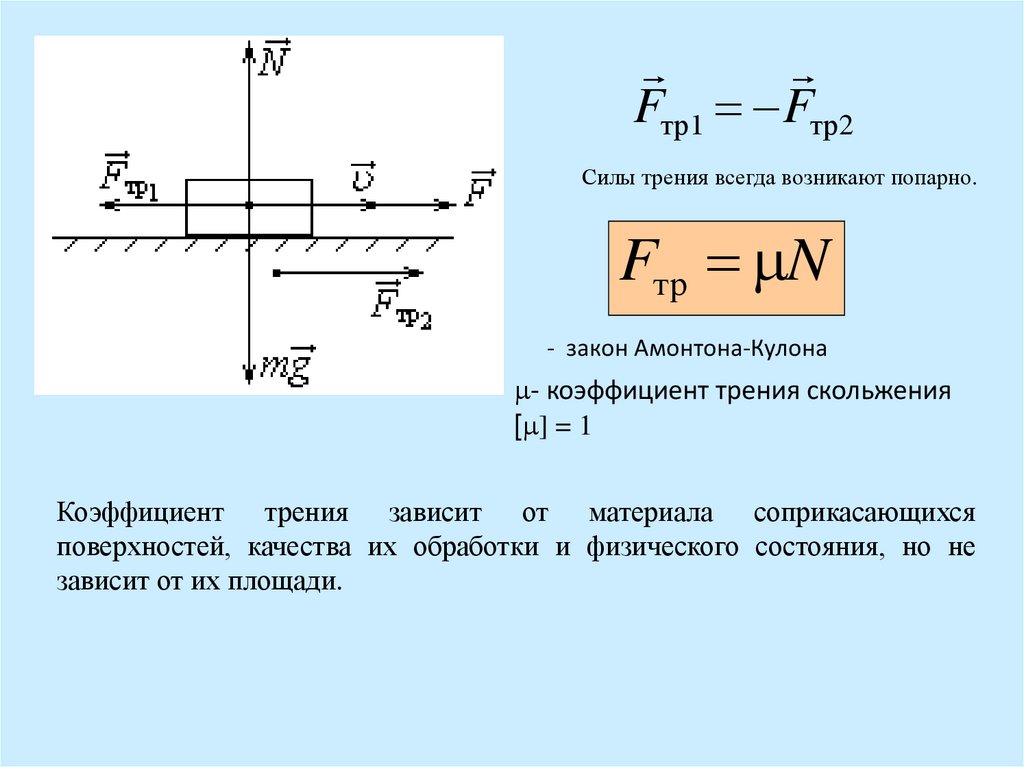
Fтр1 Fтр2Силы трения всегда возникают попарно.
Fтр N
- закон Амонтона-Кулона
- коэффициент трения скольжения
[ ] = 1
Коэффициент трения зависит от материала соприкасающихся
поверхностей, качества их обработки и физического состояния, но не
зависит от их площади.
22. Деформация кручения
В. Гравитационные силы23. Деформация сдвига
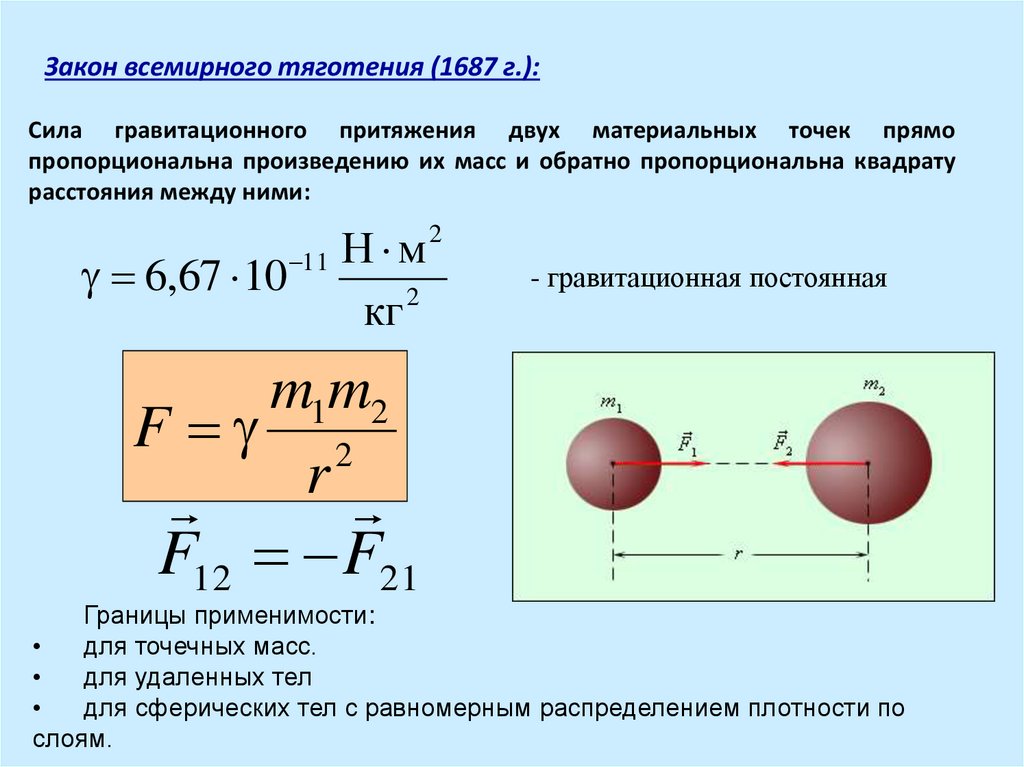
Закон всемирного тяготения (1687 г.):Сила гравитационного притяжения двух материальных точек прямо
пропорциональна произведению их масс и обратно пропорциональна квадрату
расстояния между ними:
6,67 10
11
Н м
2
кг
2
- гравитационная постоянная
m1m2
F 2
r
F12 F21
Границы применимости:
для точечных масс.
для удаленных тел
для сферических тел с равномерным распределением плотности по
слоям.
24.
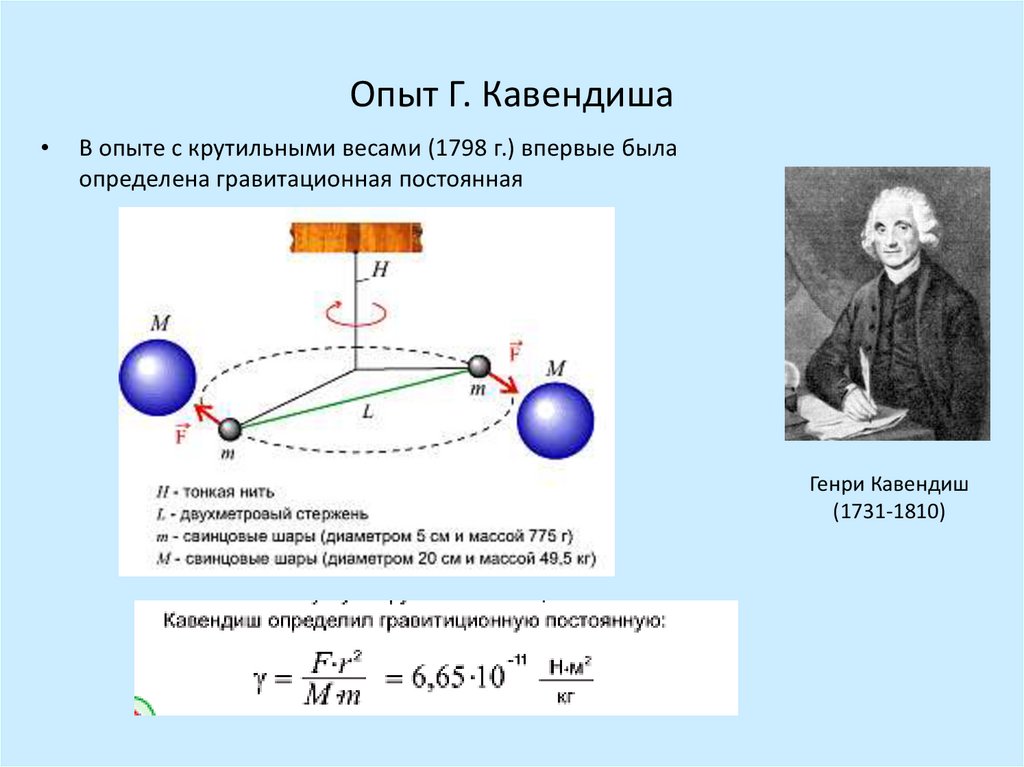
Опыт Г. КавендишаВ опыте с крутильными весами (1798 г.) впервые была
определена гравитационная постоянная
Генри Кавендиш
(1731-1810)
25. Б. Силы трения
Сила тяжестиСила тяжести Fтяж тела – это отвесная составляющая силы земного тяготения,
действующей на тело.
Fтяж mg
Fг - сила гравитационного притяжения
T - сила натяжения нити
- географическая широта местности
По теореме косинусов
Fтяж Fг2 Fц2 2 Fг Fц cos
где Fц man m
2
r
- центростремительная сила
1) полюс ( =90 ) Fтяж = Fг
2) экватор ( =0 )
Fтяж Fг
4 2 m
Rз
T02
Максимальное различие между Fтяж и Fг не превышает 0,3% Будем считать Fтяж Fг
26.
Ускорение свободного паденияПусть тело находится на поверхности Земли (r = Rз):
F
g0
MЗ
м
9
,
81
RЗ2
с2
MЗ
gh
RЗ h 2
mM З
RЗ2
F = ma
mM З
ma 2
RЗ
- ускорение свободного падения на поверхности Земли
- ускорение свободного падения на высоте h над поверхностью Земли
g зависит от:
1) высоты
2) географической широты
3) залегания горных пород
27.
Космические скоростиПервая космическая (эллиптическая) скорость – это скорость, которую необходимо
сообщить телу, чтобы оно стало искусственным спутником Земли.
mM
R32
12
F man m
RЗ
M
1 gRЗ
RЗ
F
- первая космическая скорость
1 ≈ 7,9 км/с
Вторая космическая (параболическая) скорость – это скорость, которую
необходимо сообщить телу, чтобы оно покинуло пределы Земли и стало
спутником Солнца.
Wk1 + Wp1 = Wk2 + Wp2 - ЗСЭ
mM З
m 22
0
2
RЗ
2 M З
2 M З RЗ
M
2
g 2 З 2 gRЗ 2 1
2
RЗ
RЗ
RЗ
2 = 11,2 км/с
Третья космическая скорость – это скорость, которую необходимо сообщить телу
для того, чтобы оно покинуло пределы Солнечной системы.
3 = 16,7 км/с, если тело запускать по ходу орбитального движения Земли
28. В. Гравитационные силы
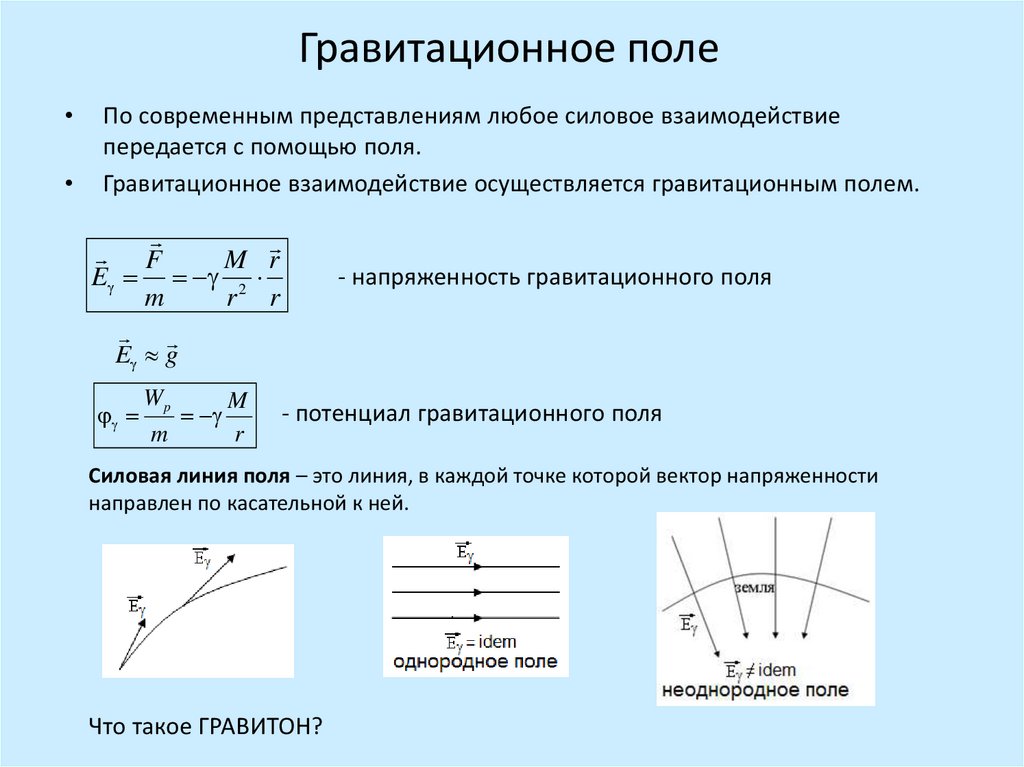
Гравитационное полеПо современным представлениям любое силовое взаимодействие
передается с помощью поля.
Гравитационное взаимодействие осуществляется гравитационным полем.
F
M
E 2
m
r
r
r
- напряженность гравитационного поля
E g
Wp
m
M
r
- потенциал гравитационного поля
Силовая линия поля – это линия, в каждой точке которой вектор напряженности
направлен по касательной к ней.
Что такое ГРАВИТОН?
29. Законы Кеплера
Г. Вес тела. Сила реакции опорыВес P тела – сила, с которой тело давит на опору или натягивает подвес
вследствие гравитационного притяжения к Земле.
• Нормальная реакция N опоры – сила, с которой опора действует на
тело в направлении, перпендикулярном к поверхности соприкосновения
тела и опоры.
Вес тела и сила реакции опоры равны по третьему закону Ньютона:
P N
В современной науке вес и масса — совершенно разные понятия: масса является
неотъемлемым свойством тела, а вес — результат действия силы тяжести на
опору.
Во многих повседневных ситуациях слово «вес» продолжает использоваться,
когда фактически речь идет о «массе».
[m] = 1 кг
[P] = 1 Н
30.
5. Центр масс.Закон сохранения импульса
31. Опыт Г. Кавендиша
Центр масс механической системы – это точка масса которой равна массесистемы, а радиус вектор задается уравнением:
m
r
ii
n
rC
i 1
n
mi
i 1
или в скалярной форме системой трех уравнений
mi xi
i
1
x
n
C
mi
i 1
n
mi yi
i 1
yC n
mi
i 1
n
mi zi
i
1
z n
C m
i
i 1
n
Центром масс или центром системы
материальных точек называется
точка С радиус-вектор которой равен
отношению суммы произведений масс
всех материальных точек системы на
их радиусы векторы к массе всей
системы.
32. Сила тяжести
Вокруг центра масс уплотнилась бы механическая система, если бысилы гравитационного притяжения возросли до бесконечности.
m2 > m1
m1 l2
m2 l1
Замкнутая механическая система – система, на которую не
действуют внешние силы.
Fi 0
Квазизамкнутая механическая система – система, на которую
n
действуют скомпенсированные внешние силы.
Fi 0 Fi 0
i 1
Незамкнутая механическая система – система, на которую действуют
n
не скомпенсированные внешние силы.
Fi 0 Fi 0
i 1
33. Ускорение свободного падения
Продифференцируем радиус-вектор центра масс и найдем скорость еедвижения:
n
n
n
d n
dri
mi ri mi
m
p
i
i
i
dt i 1
i 1
dt
i 1
i 1
rC C
n
n
n
M
mi
mi
mi
i 1
i 1
i 1
n
M C pi
i 1
n
pC pi - теорема о движении центра масс
i 1
Центр масс механической системы движется как точка, масса которой
равна массе всей системы. Импульс системы равен импульсу центра ее
масс.
34. Космические скорости
Закон сохранения импульса (ЗСИ)n
n
i 1
i 1
d m C d mi i d mi i
m C mi i
dp C d m C
F
dt
dt
n
i 1
- Закон движения центра масс
d m C Fdt
Fdt
- импульс силы
Fi 0 , тогда:
i 1
n
Если система замкнута, то
d m C 0
Закон сохранения импульса:
импульс замкнутой системы не
изменяется с течением времени:
m C mi i const
n
i 1
dp
0
dt
n
pi const - закон сохранения импульса
i 1
Геометрическая сумма импульсов тел замкнутой механической системы не
изменяется.
35. Гравитационное поле
СИЛА И ИМПУЛЬСЗапишем второй закон Ньютона
m m 0
F = ma
0
a
t
F
Ft m m 0
t
p = mv –импульс тела после взаимодействия
p0 = mv0 – импульс тела до взаимодействия
I=Ft – импульс силы
F t p p0
36. Г. Вес тела. Сила реакции опоры
• Хотя ЗСИ получен с помощью законовдинамики, он не является их следствием.
• Все
законы
сохранения
являются
универсальными, т.е. выполняются и в
макромире и в микромире.
• Согласно теореме Эмми Нётер (1918 г.)
каждому свойству симметрии физической
системы соответствует некоторый закон
сохранения.
• Закон сохранения импульса – следствие
однородности пространства.
Амалия Эмми Нётер
(1882-1935)
37. 5. Центр масс. Закон сохранения импульса
6. Реактивное движение.Уравнение Мещерского.
Формула Циолковского
38.
Уравнение Мещерского• Реактивное движение - движение тела, при котором от него
отделяется (присоединяется) некоторая его часть.
Рассмотрим движение ракеты:
В момент времени t:
m – масса ракеты,
- скорость ракеты,
В момент времени t + dt:
m + dm – масса ракеты,
+ d - скорость ракеты,
- dm – масса выброшенных газов
(dm < 0),
u – скорость истечения газов
относительно ИСО
39.
Используем второй закон Ньютона:dp
F
dt
p p0 Fdt
dp Fdt
где
p0 - импульс системы в начальный момент времени t,
p - импульс системы в момент времени t + dt.
(m dm)( d ) ( dmu ) m Fdt
d
m md dm dm d dm u m Fdt
dt
dm d 0
dm
d
( u ) m
F
dt
dt
d dm
m
F
(u )
dt
dt
40.
V u- скорость истечения газов относительно ракеты.
d dm
m
F
V
dt
dt
dm
Fреакт
V
dt
- уравнение Мещерского
- реактивная сила
d
m
F Fреакт
dt
Иван
Всеволодович
Мещерский
(1859-1935)
41.
Формула ЦиолковскогоF 0
Пусть система замкнута
d dm
m
V
dt
dt
В проекциях на направление движения:
m
d
dm
V
dt
dt
(dm < 0)
Разделим переменные:
d V
dm
m
dm
d V m
m
m
0
V ln
m0
m
Константин
Эдуардович
Циолковский
(1857-1935)
- формула Циолковского
где m0 – стартовая масса ракеты (вместе с топливом);
m = m0 – mтоп – полезная масса (масса ракеты без топлива).
Пусть V 1 км/с, = I = 7,9 км/с
m0
= 2697
m



































 physics
physics








