Динамика вращательного движения (динамика абсолютно твёрдого тела)

1. Динамика вращательного движения (динамика абсолютно твёрдого тела)

ВоГТУ
Лекция 3
Динамика вращательного
движения (динамика
абсолютно твёрдого тела)
Кузина Л.А.,
к.ф.-м.н., доцент
2015 г.

2. План

1. Закон динамики вращательного движения
A. Момент силы
B. Момент пары сил
C. Момент инерции
2. Моменты инерции некоторых тел:
A. Кольцо (тонкостенный цилиндр)
B. Толстостенный цилиндр
C. Сплошной цилиндр
D. Шар
E. Тонкий стержень
3. Теорема Штейнера
4. Момент импульса тела. Закон сохранения и
закон изменения момента импульса; импульс
момента силы
5. Работа при вращательном движении
6. Кинетическая энергия вращения
7. Сопоставление величин и законов для
поступательного и вращательного движения

3.

Рассматривается твёрдое тело, которое может вращаться вокруг
неподвижной оси
Запишем второй закон Ньютона для отдельной элементарной массы Δmi
Fik mi aik
Fin - нормальная составляющая
равнодействующей силы
Fik - касательная составляющая
равнодействующей силы
aik ri
Fik mi ri
Fik ri mi ri ri
Fik ri Fi sin ri Fi li
M i mi ri2

4.

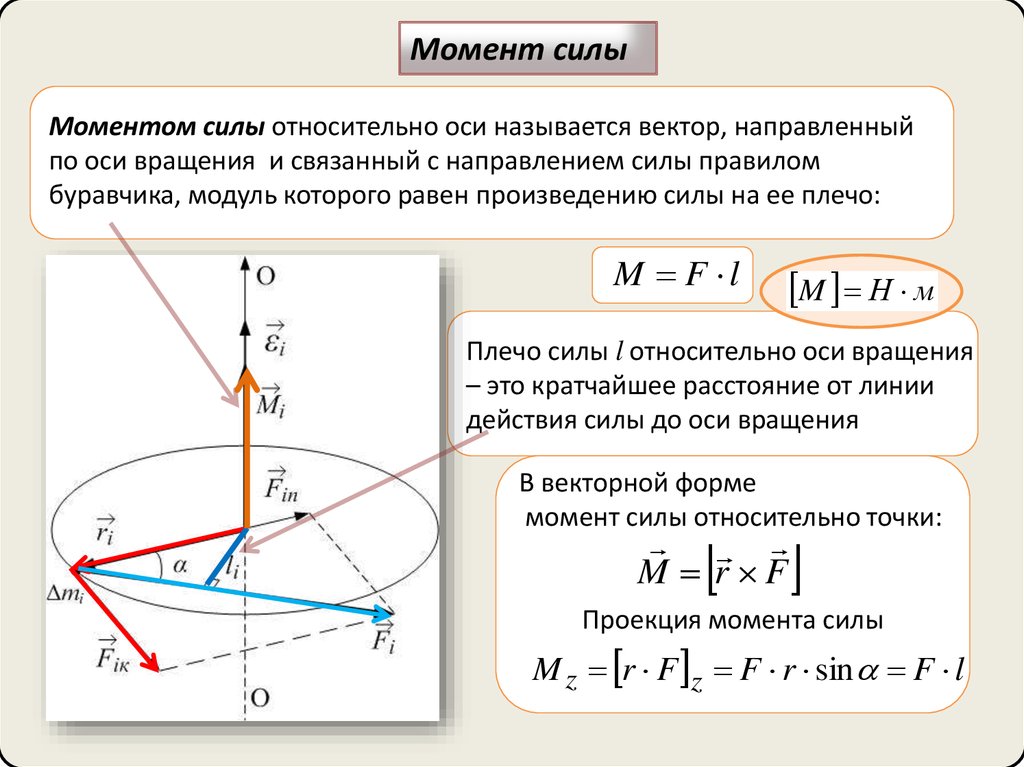
Момент силы
Моментом силы относительно оси называется вектор, направленный
по оси вращения и связанный с направлением силы правилом
буравчика, модуль которого равен произведению силы на ее плечо:
M F l
M Н м
Плечо силы l относительно оси вращения
– это кратчайшее расстояние от линии
действия силы до оси вращения
В векторной форме
момент силы относительно точки:
M r F
Проекция момента силы
M z r F z F r sin F l

5.

Момент пары сил
Пара сил – это две равные по
величине и противоположные
по направлению силы, линии
действия которых не
совпадают
Плечо пары сил
Суммарный момент пары сил в проекции на ось,
проходящую через точку О:
M F2 l2 F1 l1 F l1 l F l1 F l

6.

Закон динамики вращательного движения
Скалярная величина I, равная произведению
массы материальной точки на квадрат её
расстояния до оси, называется
M i mi ri2
моментом инерции материальной
точки относительно оси ОО:
M i Ii
Суммируем по всем
элементарным массам, на
которые разбито тело
2
M
m
r
i
ii
i
I mr 2
I кг м2
Момент инерции твёрдого
тела:
2
I mi ri
i
i
внешних
Mi M
i
внешн.
M
I

7.

Закон динамики вращательного движения
внешн.
M
I
внешн.
M
I
Угловое ускорение тела прямо
пропорционально суммарному
моменту внешних сил и обратно
пропорционально моменту
инерции тела
Аналог для поступательного движения:
внешн.
F
a
m
Ускорение тела прямо пропорционально
равнодействующей внешних сил и обратно
пропорционально массе тела
Момент инерции I твердого тела является
мерой инертных свойств твердого тела при
вращательном движении и аналогичен
массе тела m во втором законе Ньютона.

8.

Момент инерции I
- зависит от массы тела и от её
распределения относительно оси вращения
- характеризует инертные свойства тела при
вращательном движении
I mr 2
I mi ri2
для материальной точки
для твёрдого тела (для системы точечных масс)
i
I r 2dm r 2 dV
m
V
для твёрдого тела (если масса распределена непрерывно)

9.

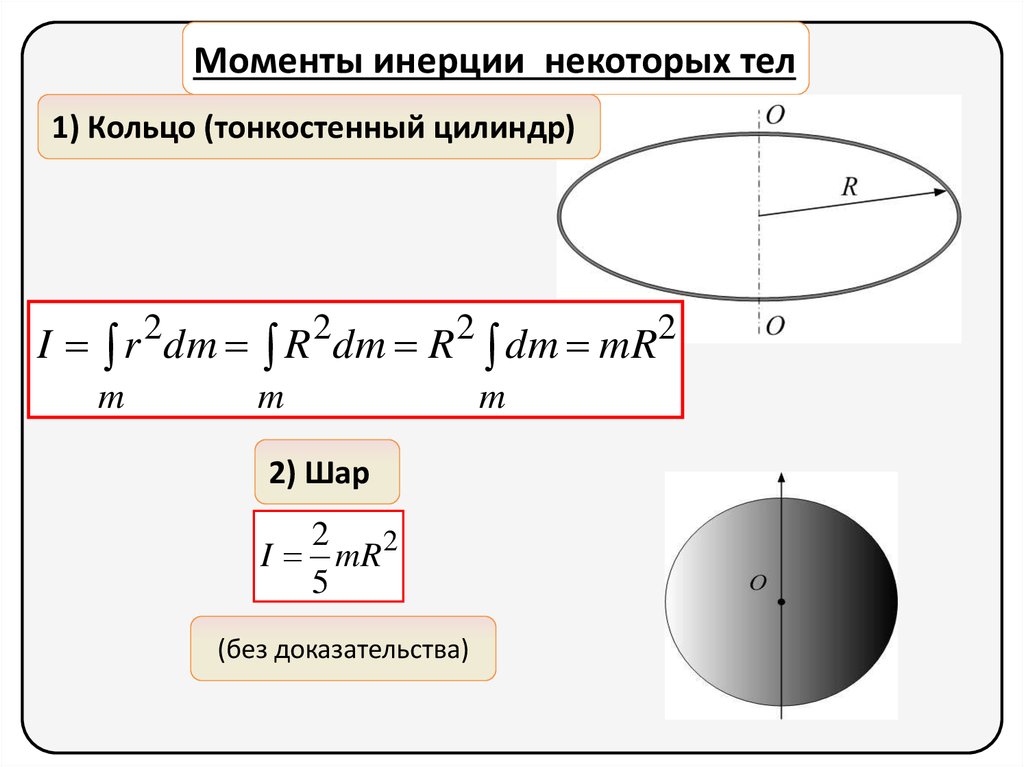
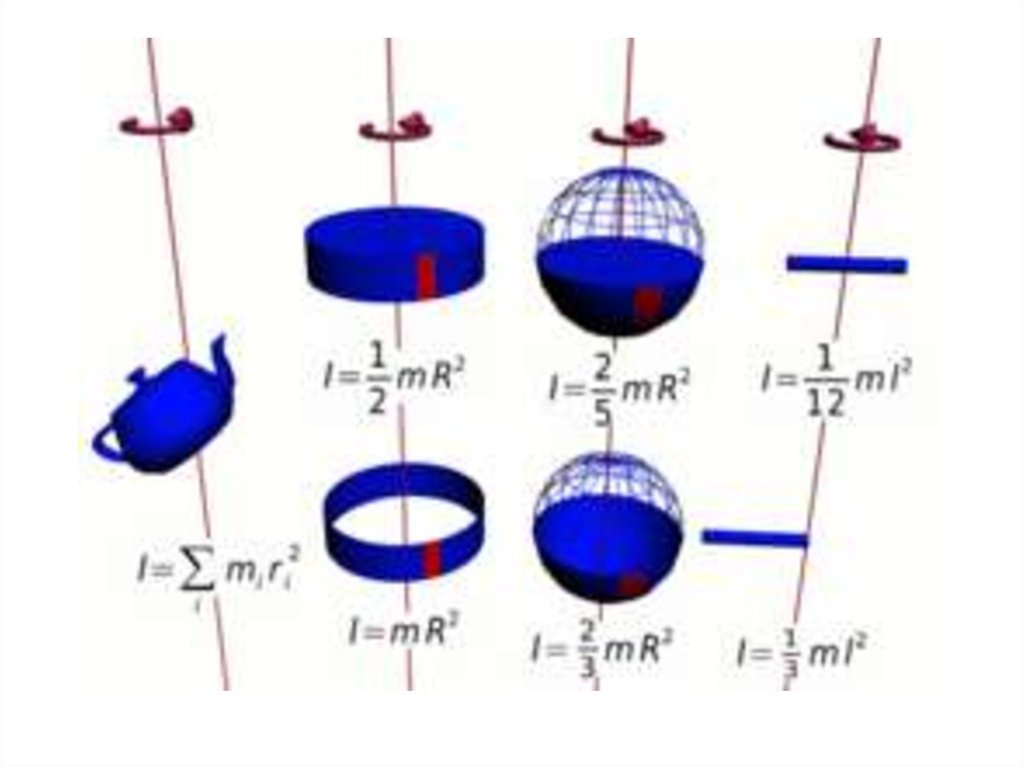
Моменты инерции некоторых тел
1) Кольцо (тонкостенный цилиндр)
I r 2dm R 2dm R 2 dm mR2
m
m
2) Шар
2
I mR 2
5
(без доказательства)
m

10.

3)Сплошной цилиндр (диск) dm dV h 2 r dr
R
I r dm r 2 h 2 r dr
2
m
0
R
I 2 h r 3dr
0
r4
R
I 2 h
4
0
I
h R4
2
R2 h R2
2
mR 2
I
2
V R2
2
m R2
2

11.

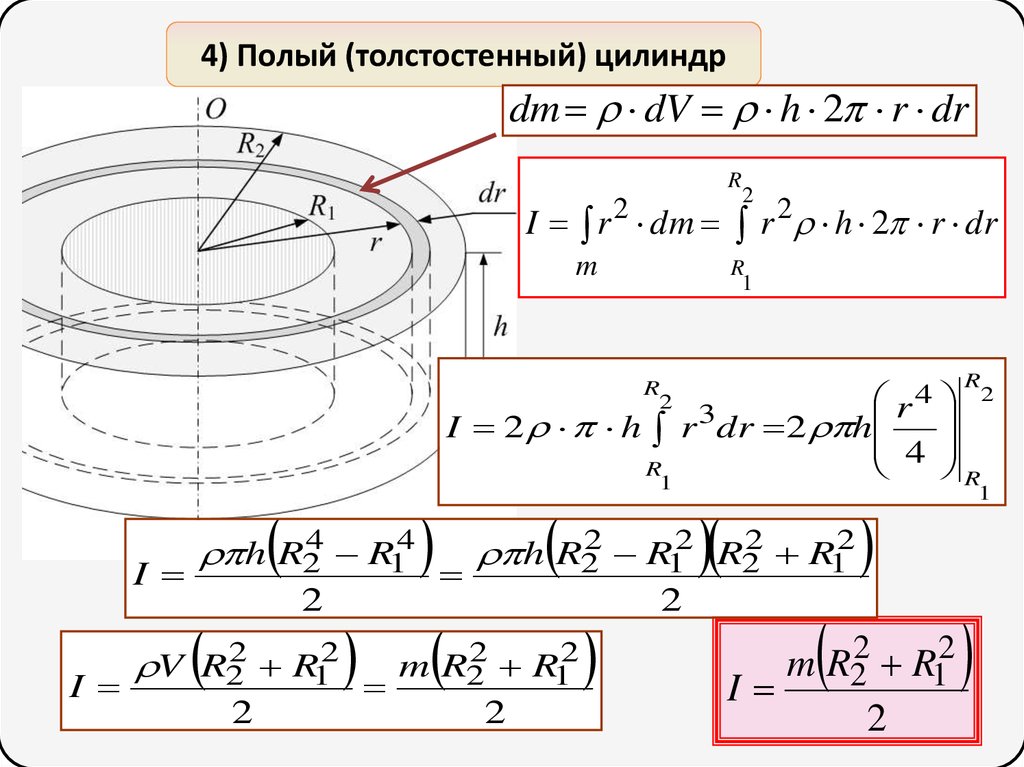
4) Полый (толстостенный) цилиндр
dm dV h 2 r dr
R
2
I r dm r 2 h 2 r dr
2
m
R
1
R
r4
2
R
I 2 h r 3dr 2 h
4
R
R
1
I
I
h R24 R14
2
V R22 R12
2
1
h R22 R12 R22 R12
m R22 R12
2
2
m R22 R12
I
2
2

12.

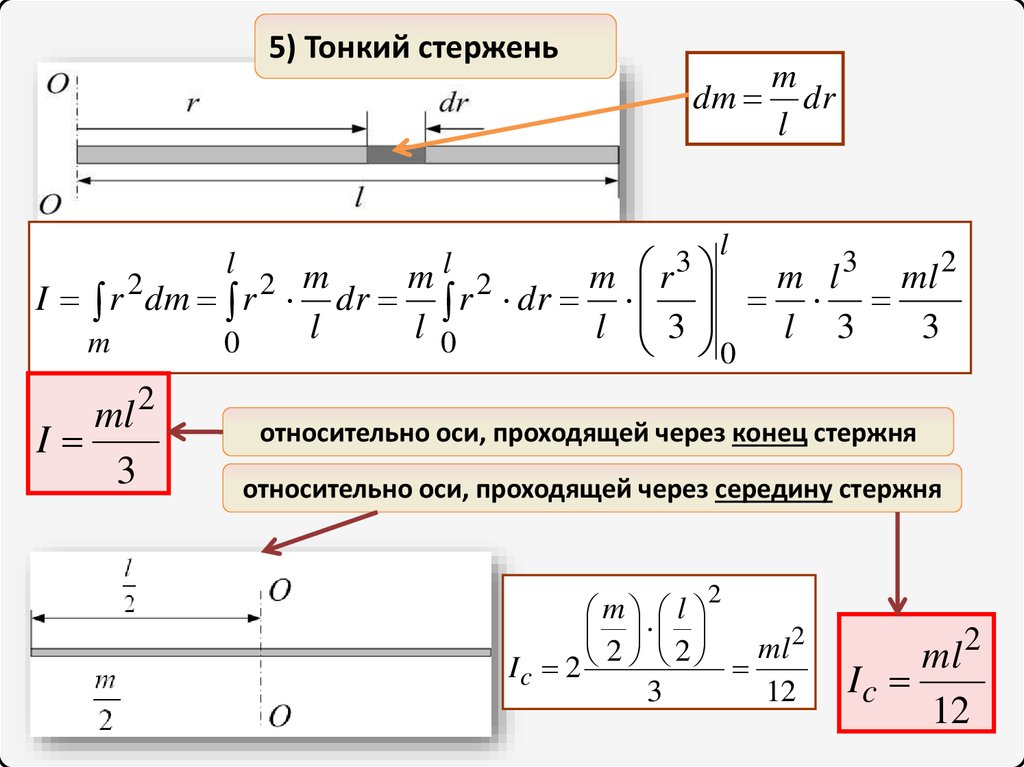
5) Тонкий стержень
m
dm dr
l
m r 3
l
3
2
l
m
m
m
l
ml
I r 2 dm r 2 dr r 2 dr
3
l
l
l
3
m
0
0
0 l 3
ml 2
l
I
относительно оси, проходящей через конец стержня
3
относительно оси, проходящей через середину стержня
2
m l
ml 2
2 2
Ic 2
3
12
ml 2
Ic
12

13.

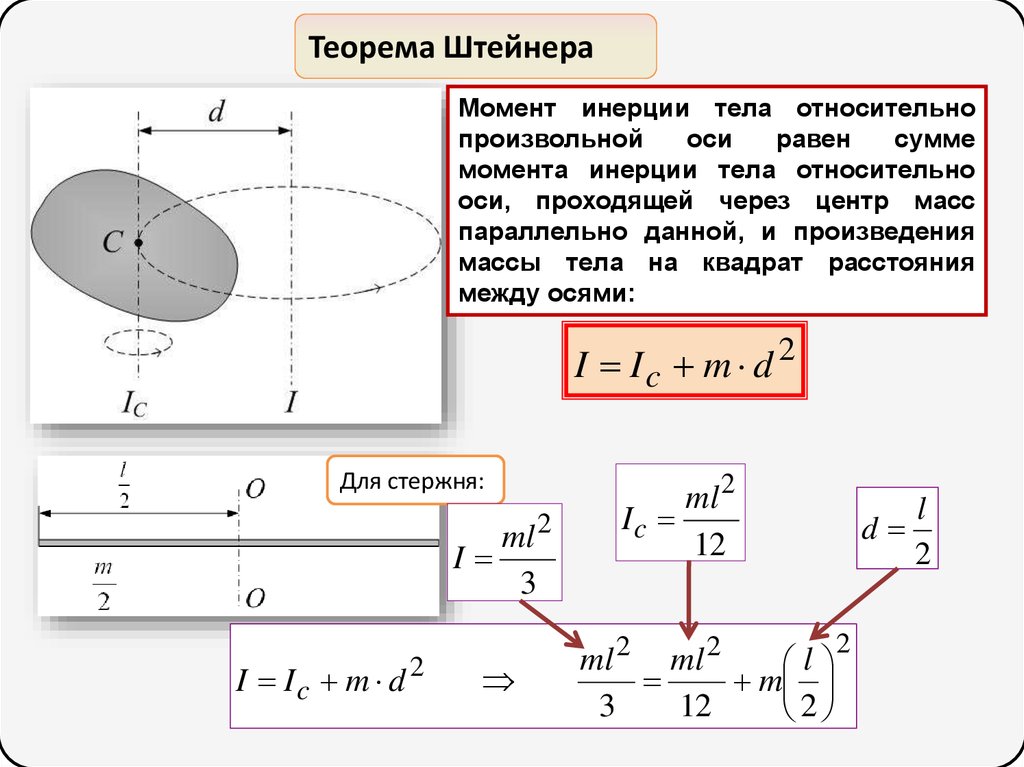
Теорема Штейнера
Момент инерции тела относительно
произвольной
оси
равен
сумме
момента инерции тела относительно
оси, проходящей через центр масс
параллельно данной, и произведения
массы тела на квадрат расстояния
между осями:
I Ic m d 2
Для стержня:
I
I Ic m d 2
ml
3
2
ml 2
Ic
12
ml 2 ml 2
l
m
3
12
2
d
2
l
2

14.

15.

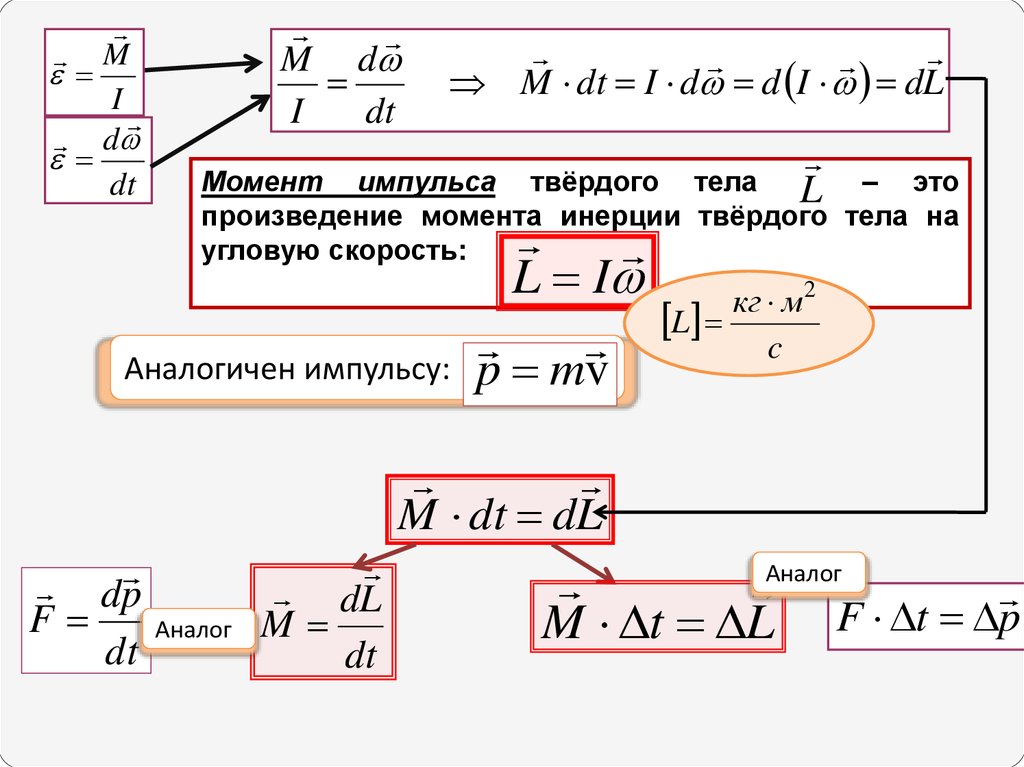
M
I
d
dt
M d
I
dt
M dt I d d I dL
L
Момент импульса твёрдого тела
– это
произведение момента инерции твёрдого тела на
угловую скорость:
Аналогичен импульсу:
L I
кг м 2
L
c
p mv
M dt dL
dp
F
dt
Аналог
dL
M
dt
Аналог
M t L F t p

16.

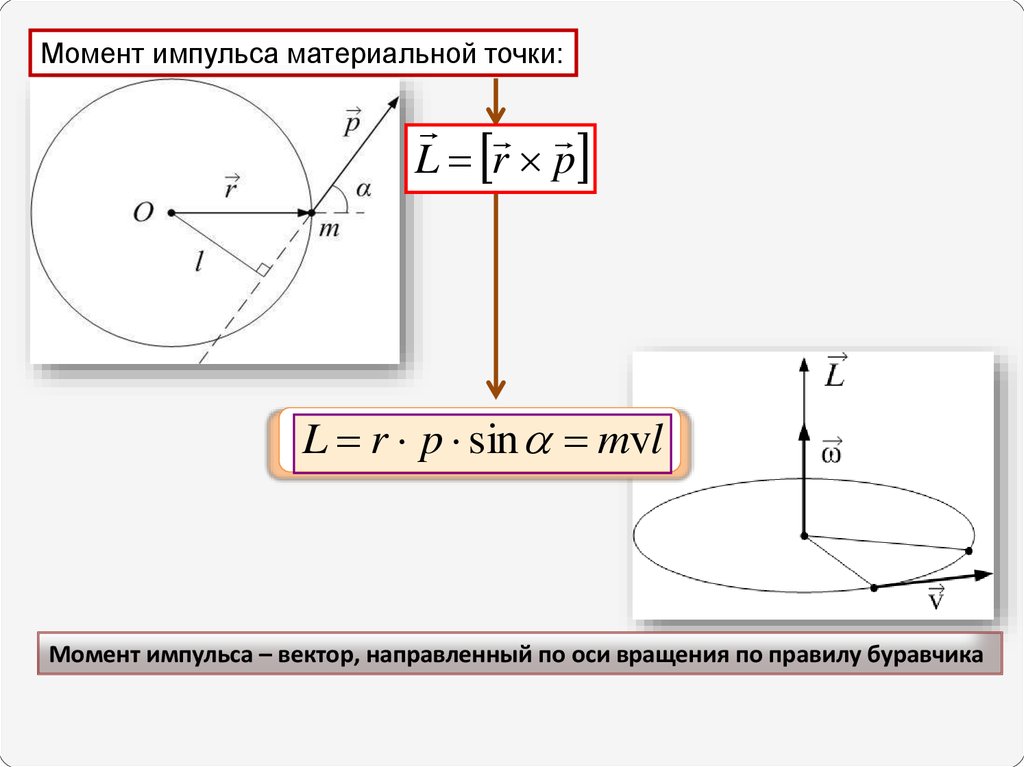
Момент импульса материальной точки:
L r p
L r p sin mvl
Момент импульса – вектор, направленный по оси вращения по правилу буравчика

17.

Момент импульса твёрдого тела
Для расчёта момента импульса
вращающегося
твёрдого тела
найдём сумму L по всем
i
материальным точкам:
L
L Li ri mi vi ri mi ri mi ri2 I
i
i
i
i
Определения эквивалентны:
L r p
L I

18.

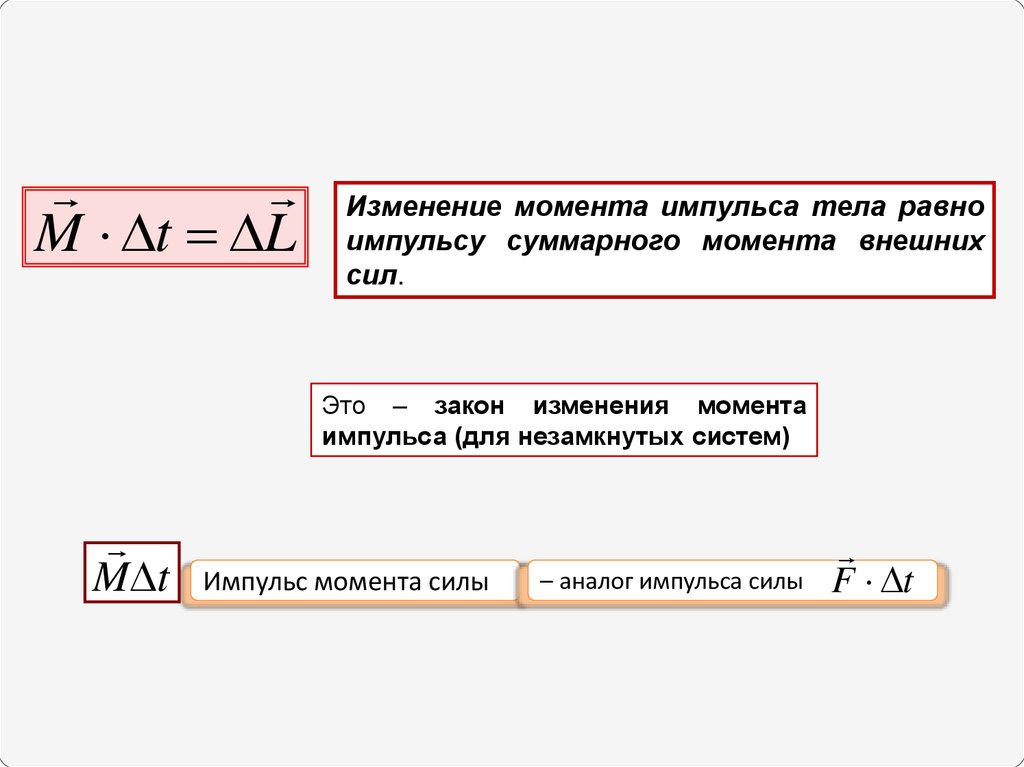
M t L
Изменение момента импульса тела равно
импульсу суммарного момента внешних
сил.
Это – закон изменения момента
импульса (для незамкнутых систем)
M t
Импульс момента силы
– аналог импульса силы
F t

19.

Закон сохранения момента импульса:
Если
внешн.
0
M
L const
Это возможно, если:
система замкнута (или
внешн.
0 )
F
у внешних сил нет касательных
составляющих (вектор силы проходит
через ось или центр вращения)
внешние силы параллельны закреплённой оси вращения

20.

Закон сохранения момента импульса:
Если
внешн.
0
M
L const
У внешних сил нет касательных составляющих (вектор силы
проходит через ось или центр вращения)
– поле центральных сил (гравитация)
Примеры:

21.

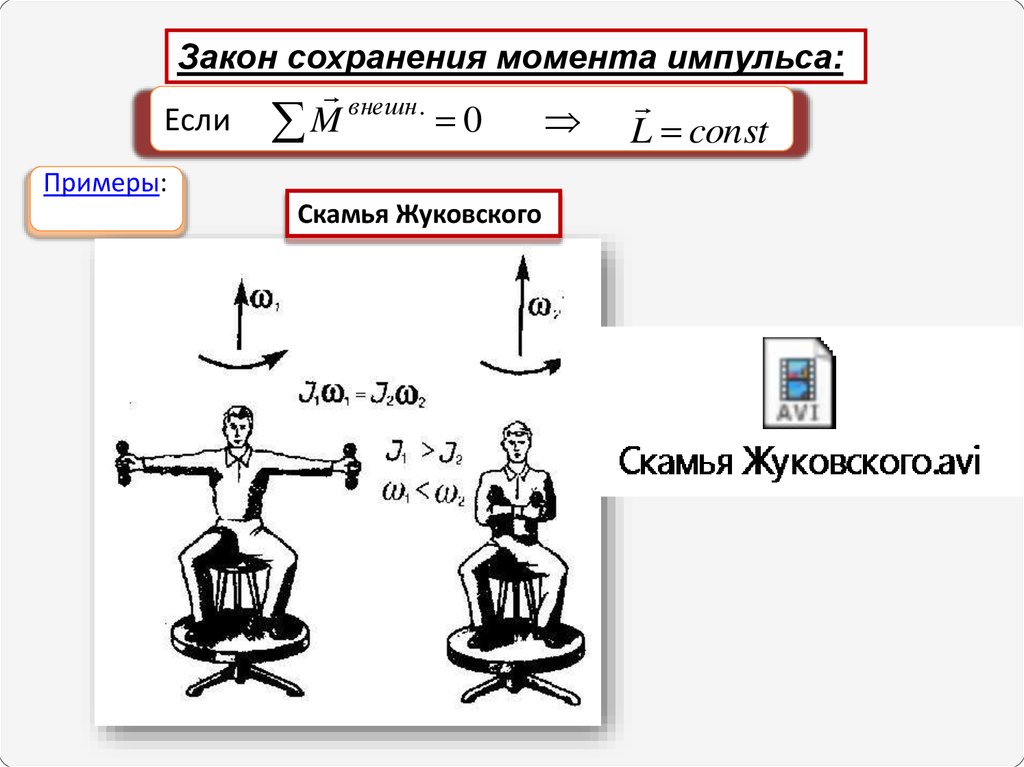
Закон сохранения момента импульса:
Если
внешн.
0
M
Примеры:
Скамья Жуковского
L const

22.

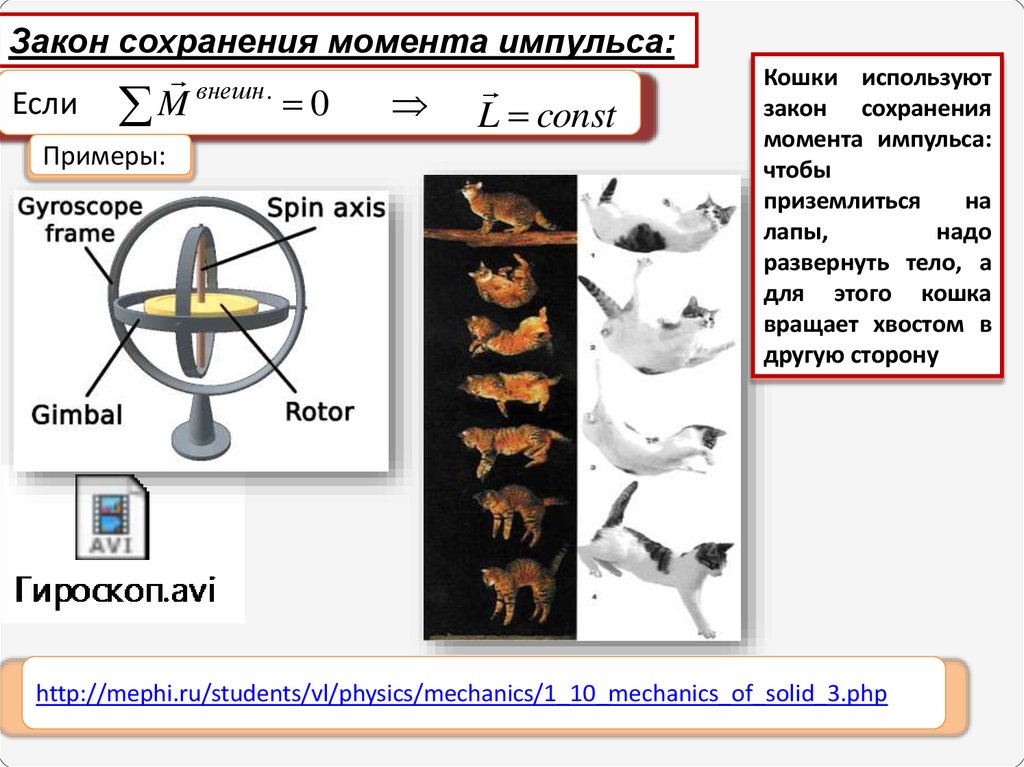
Закон сохранения момента импульса:
Если
внешн.
0
M
Примеры:
L const
Кошки используют
закон сохранения
момента импульса:
чтобы
приземлиться
на
лапы,
надо
развернуть тело, а
для этого кошка
вращает хвостом в
другую сторону
http://mephi.ru/students/vl/physics/mechanics/1_10_mechanics_of_solid_3.php

23.

Работа при вращательном движении
Пусть тело повернулось
на угол d под
действием силы F
– угол между силой и перемещением dS
r – радиус-вектор точки приложения силы
Работа силы:
dA F dS F cos dS
dS r d
dA F cos r d F l d
M F l
2
2
1
1
A dA M d
dA M d

24.

Кинетическая энергия вращения
Пусть тело вращается относительно закреплённой оси с угловой
скоростью . Разобьём его мысленно на элементарные массы mi
и просуммируем кинетические энергии:
mi vi2
W Wi
i
i 2
v r
mi 2 ri2 2
W
mi ri2
2
2 i
i
I mi ri2
i
I 2
W
2
Для катящегося тела:
m vc2 I 2
Wкин. Wпост. Wвращ
2
2
Скорость центра масс

25.

Аналогия между поступательным и вращательным движениями

26.

Аналогия между поступательным и вращательным движениями

27.

Закон сохранения момента импульса (старый советский фильм)
http://www.youtube.com/watch?v=reVVfgexHvw
Закон сохранения момента импульса (скамья Жуковского)
http://www.youtube.com/watch?v=hwlwfJMAvYw
http://www.youtube.com/watch?v=8BB5sWXBKos
Гирокомпас в карданном подвесе
http://www.youtube.com/watch?v=W6ii5GlLlNA
Гироскоп
http://www.youtube.com/watch?v=UpTGaalydXo
Второй закон Кеплера