Similar presentations:
Динамика твёрдого тела
1. ГЛАВА I. МЕХАНИКА §5. Динамика твёрдого тела
О. И. ЛубенченкоНИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020
2. §5. Динамика твёрдого тела
2I. Момент силы
Момент силы — векторная (псевдовекторная) ФВ, характеризующая
взаимодействие тел.
1. Момент силы относительно точки
Момент силы относительно точки:
A ⊗M
M rF
Точка O — полюс.
M
M rF sin r , F
O
Н м
z
2. Момент силы относительно оси
M rF k
k h
O
z
M rFxy sin r , Fxy
Плечо силы — скалярная ФВ — кратчайшее
расстояние от оси до линии действия силы.
h r sin r , Fxy
F
r
M hFxy
F
D
r
A
Fxy
xy
M
3. §5. Динамика твёрдого тела
3II. Основное уравнение динамики вращательного движения
e
i
z
II
закон
Ньютона
для
i-ого
фрагмента:
Δ
m
a
F
F
e
ki
i i
i
Fi
k i
ω
e
i
r F r F ki
Δ
m
r
a
i i i
ε
i i k i i
Oi
r F iki M iki a εr ω ωr
r F e M e
ri Δmi
i
i i
i
i
i
i
k i
k i
Двойное векторное произведение: a bc b ac c ab
ri ai r i εri ri ω ωri εri2 ri εri ri ω ωri ri ω2
0
0
εri ω ri ri εri2
2
2
e
Δmi ri ε Mi M
2
i
ki
k i
Δm r
2
i i
i
e
ε Mi M
i
i
ε Δmi ri Mi
2
i
i
k i
e
i
ki
0
4. §5. Динамика твёрдого тела
4I Δmi ri2 — момент инерции тела относительно оси
i
Iε M — основное уравнение динамики вращательного движения
Основное уравнение динамики вращательного движения можно записать и
относительно подвижной оси, проходящей через центр масс тела (доказать
самостоятельно).
III. Момент инерции
M
При Δmi → 0 I r dm
2
I кг м2
0
Момент инерции — мера инертности тела во вращательном движении —
скалярная ФВ, зависящая от формы и размеров тела. Момент инерции —
аддитивная величина.
M
Момент инерции тела относительно точки: I r 2dm
0
M
Момент инерции тела относительно оси: I r 2dm
0
5. §5. Динамика твёрдого тела
ПРИМЕРЫ РАСЧЁТА МОМЕНТА ИНЕРЦИИ1. Тонкое кольцо (полый цилиндр)
Найти момент инерции тонкого однородного кольца массы m и радиуса R
относительно его оси.
z
Разобьём кольцо на бесконечно малые элементы — дуги
m
O
R
массой dm.
2
Элементарный момент инерции dI dm R
m
I R 2dm mR 2
dm
0
2. Тонкий стержень
Найти момент инерции тонкого однородного стержня массы m и длины l
относительно оси: а) проходящей через середину стержня перпендикулярно
ему, б) проходящей через один из концов стержня перпендикулярно ему.
dm τdr
m
— линейная плотность
l
m
dI dm r 2 r 2dr
l
τ
5
6. §5. Динамика твёрдого тела
а)z
l2
m, l
O
r
m 2
2m r 3
I 2 r dr
l
l 3
0
dm
dr
б) z
l
r
O
dm
0
2ml 3 ml 2
3l 8 12
3 l
m
mr
I r 2dr
l
l 3
0
m, l
dr
l2
ml 3 ml 2
3l
3
0
3. Однородный диск (сплошной цилиндр)
Найти момент инерции однородного диска массы m и радиуса R относительно
его оси.
z
2
m
dm
dr
dI dm r
dm σdS
dS 2πrdr
r O
R
σ
m
— поверхностная плотность
2
πR
7. §5. Динамика твёрдого тела
m2m 3
2
2
πrdr
r
r dr
2
2
πR
R
R
R
2m 3
2m r 4
mR 2
I 2 r dr 2
R
R 4 0
2
0
dI
4. Однородная сфера
Найти момент инерции однородной сферы массы m и радиуса R
относительно оси, проходящей через её центр.
z
2
2
2
r
m
O
R
x
dI z dm r dm x y
dm
dI x dm y 2 z 2
y
z
dI y dm x 2 z 2
dI0 dm R 2 dm x 2 y 2
2
8. §5. Динамика твёрдого тела
m2
2
I z x y dm
0
m
2
2
I x y z dm
0
m
I y x 2 z 2 dm
0
m
I0
0
m
1
x 2 y 2 z 2 dm 2x 2 2 y 2 2z 2 dm
20
m
m
m
3
1
2
2
2
2
x y dm y z dm x 2 z 2 dm I z
2 0
0
0
2
Iz
Ix
2
2
I z I0 mR 2
3
3
Iy
5. Однородный шар
Найти момент инерции однородного шара массы m и радиуса R
относительно оси, проходящей через его центр.
2
I mR 2 (доказать самостоятельно)
5
9. §5. Динамика твёрдого тела
Теорема ШтейнераМомент инерции тела относительно некоторой оси равен сумме момента
инерции этого тела относительно оси, проходящей через центр масс тела
параллельно данной оси, и произведения массы тела на квадрат расстояния
между осями:
I IC md 2
Доказательство
Разобьём тело на малые фрагменты массы dm.
zC
dm
dm
C
r ρ d
z
d
zC ⊙
ρ
r
d
2
ρ2dm d 2dm 2ρd dm
m
m
I ρ2dm d 2 dm 2d ρdm IC md 2
0
IC
dI ρ d dm ρ2 2ρd d 2 dm
⊙z
m
dIC ρ2dm
dI r 2dm
0
m
0
0, т. к. C — центр масс
10. §5. Динамика твёрдого тела
IV. Пример решения задачи по динамикеМаятник Обербека
Маятник Обербека — тело вращения сложной формы — маховик с
несколькими шкивами и четырьмя радиально направленными спицами, на
которые надеваются небольшие грузы, положение которых можно
изменять.
На шкив радиуса R намотана нить, на конце которой прикреплён груз
массы M. Масса грузов на спицах равна m, они расположены на расстоянии
r от оси маятника; момент инерции маховика со спицами относительно оси
маятника равен I0. Груз массы M поднимают на расстояние h над полом и
отпускают. Через какое время груз коснётся пола?
Объекты исследования: груз массы M — МТ; маятник с грузами массы m —
ТТ
ИСО — лабораторная
11. §5. Динамика твёрдого тела
Nm
m
r
O ⊗z
y : Ma Fт1 Т 1
y :0 Fт2 N Т 2
z : Iε T R
2
F т2
T1
F т1 a
τ
Дополнительные соотношения:
t=0
M
h
Iε M Fт2 M N M T2
ОУДВД (для маятника):
m
T2
m
Т. о движении ЦМ (для маятника): 0 F т2 N T2
⊗ M T2
⊗ε
R
Ma F т1 T1
II закон Ньютона (для груза):
(закон всемирного тяготения)
Fт1 Mg
0
T2 T1 T (нить невесома)
a
(нить нерастяжима и не проскальзывает
ε
по шкиву)
R
I I0 4mr 2
y
Ma Mg T
2 a
I
4
mr
TR
0
R
12. §5. Динамика твёрдого тела
IT M g a
2
2
2
4
mr
a
MgR
MaR
0
MgR 2
a
I0 4mr 2 MR 2
2
at
Закон равноускоренного движения МТ (для груза): r t r v t
0
0
2
2
at
y t
2
aτ 2
2h
τ
При t = τ: y τ h
a
2
τ
2h I0 4mr 2 MR 2
MgR 2
13. §5. Динамика твёрдого тела
V. Динамика плоского движения твёрдого телаКачение без проскальзывания — плоское движение, при котором
скорость точек тела, соприкасающихся с опорной поверхностью,
относительно этой поверхности, равна нулю. Ось, проходящая через эти
точки, неподвижна и называется мгновенной осью вращения.
(Ускорения точек мгновенной оси не равны нулю!)
v
C
C
⊗
z
ПРИМЕР
Скатывание цилиндра с наклонной плоскости
Цилиндр массы m и радиуса R, момент инерции которого относительно его
оси равен IC, скатывается без проскальзывания с плоскости, наклонённой к
горизонту под углом α. Найти ускорение центра масс цилиндра.
Объект исследования: цилиндр — ТТ
ИСО — лабораторная
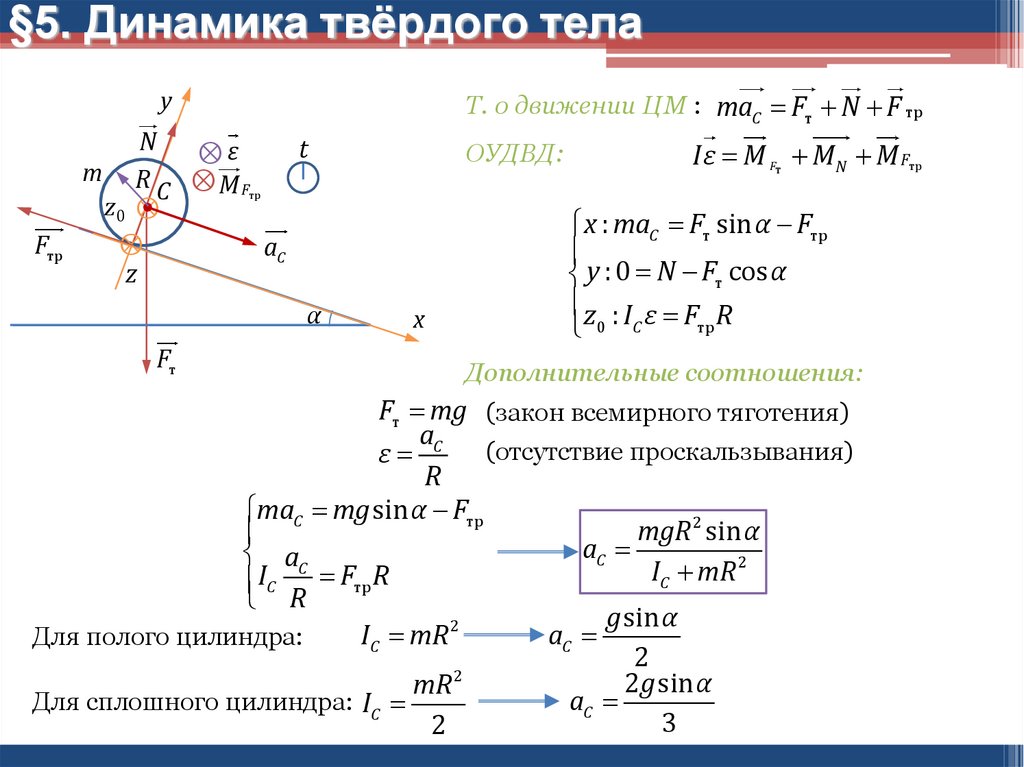
14. §5. Динамика твёрдого тела
yFтр
Т. о движении ЦМ : maC Fт N F тр
N
t
⊗ε
m R
C ⊗ M Fтр
z0 ⊗
⊗
aC
z
α
Fт
ОУДВД:
x
Iε M Fт M N M Fтр
x : maC Fт sin α Fтр
y :0 N Fт cos α
z : I ε F R
тр
0 C
Дополнительные соотношения:
Fт mg (закон всемирного тяготения)
a
(отсутствие проскальзывания)
ε C
R
maC mg sin α Fтр
mgR 2 sin α
aC
aC
2
I
mR
I
F
R
C
C
тр
R
g sin α
2
aC
IC mR
Для полого цилиндра:
2
2
2 g sin α
mR
aC
Для сплошного цилиндра: IC
3
2
15. §5. Динамика твёрдого тела
VI. Момент импульсаIε M
dω
ε
dt
dL
M
dt
dω
I
M
dt
M
d Iω
dt
— основное уравнения динамики вращательного
движения в дифференциальной форме
L Iω — момент импульса твёрдого тела относительно оси
кг м2
L с
dL
При M 0
0
dt
— закон сохранения момента импульса: момент импульса замкнутой
системы относительно любой неподвижной оси не изменяется с течением
времени.














 physics
physics








