Similar presentations:
Вращательное движение твёрдого тела
1. Вращательное движение твёрдого тела
ВРАЩАТЕЛЬНОЕДВИЖЕНИЕ
ТВЁРДОГО ТЕЛА
Карлов Р.П. Мамонтов Д.А.
Леденёв В.П.
2014
2. Введение
Вращательным движениемтвёрдого тела или системы тел
называется такое движение, при
котором все точки движутся по
окружностям, центры которых
лежат на одной прямой,
называемой осью вращения, а
плоскости окружностей
перпендикулярны оси вращения.
Ось вращения может
располагаться внутри тела и за
его пределами и в зависимости
от выбора системы отсчёта может
быть как подвижной, так и
неподвижной.
Теорема вращения Эйлера
утверждает, что любое вращение
трёхмерного пространства имеет
ось.
Примеры: роторы турбин, шестерни и
валы станков и машин и др.
2
3. Оглавление
Кинематика вращательного движения……………………….…….4Динамика вращательного движения……………………………….13
Основное уравнение динамики вращательного движения……14
Динамика произвольного движения………………………………..……….26
Законы сохранения …………………………………………………….....30
Закон сохранения момента импульса…………………………………….31
Кинетическая энергия вращающегося тела…………………………….52
Закон сохранения энергии………………………….………………………….…57
Заключение…………………………………………………………………..…..61
Использованные информационные материалы..…………...66
3
4. Кинематика вращательного движения твёрдого тела
«Для составления физических представлений следуетосвоиться с существованием физических аналогий.
Под физической аналогией я понимаю то частное
сходство между законами двух каких-нибудь областей
науки, благодаря которому одна из них является
иллюстрацией для другой»
Максвелл
КИНЕМАТИКА
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЁРДОГО ТЕЛА
4
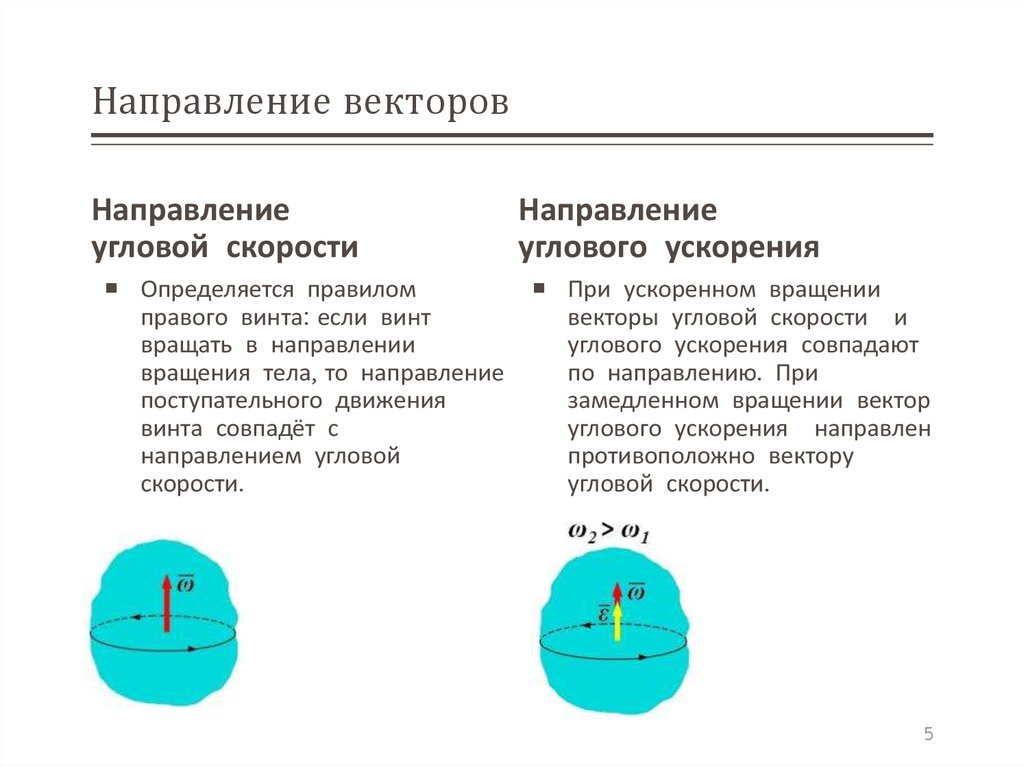
5. Направление векторов
Направлениеугловой скорости
Определяется правилом
правого винта: если винт
вращать в направлении
вращения тела, то направление
поступательного движения
винта совпадёт с
направлением угловой
скорости.
Направление
углового ускорения
При ускоренном вращении
векторы угловой скорости и
углового ускорения совпадают
по направлению. При
замедленном вращении вектор
углового ускорения направлен
противоположно вектору
угловой скорости.
5
6. Аналогия движений
Поступательное движениеВращательное движение
Перемещение
s , s м
Скорость
s
м
,
t
с
Ускорение
Угловое перемещение
a
,
t
а
м
с2
Угловая скорость
Угловое ускорение
, рад
,
t
рад
,
t
рад
2
с
с
Прямая задача кинематики: по
заданному как функция времени углу
поворота φ = f(t) найти угловые скорость
и ускорение.
Обратная задача: по заданному как
функция времени угловому ускорению ε =
f(t) и начальным условиям ω0 и φ0 найти
кинематический закон вращения.
6
7. Аналогия движений
Характеристикидвижения
Период
Частота
Угловая скорость
Угловое ускорение
Перемещение
Линейная скорость
Нормальное ускорение
Тангенциальное ускорение
Полное ускорение
Движение
материальной точки по
окружности
Вращательное
движение
твёрдого тела
t
N
N 1
t T
2
2
t
Т
2
2 2 2
t
Т
T
s r
S r
r
t
t
an
2
2r
r
r
a
r
t
t
a a 2 an2
7
8. Направление векторов скорости и ускорения
Пример:движение против
часовой стрелки
Нормальное ускорение
Угловая скорость
По радиусу к центру окружности
const
2 1
2 1
Направление: перпендикулярно плоскости рисунка, из-за плоскости
Линейная скорость
const
2 1
2 1
По касательной в направлении движения
Тангенциальное ускорение
нет
Угловое ускорение
нет
a
a
8
9. Формулы кинематики вращательного движения
ПоступательноеВращательное
Равномерное
а 0
0
const
const
s t
t
Равнопеременное
а
0
t
const
0 а t
t
const
0 t
t 2
0t
2
a t
2
2
2
0 2а s
s 0t
0
2
0 2
2
2
Неравномерное
s f (t )
s ds
lim
s (t )
t 0 t
dt
d
a lim
(t )
t 0 t
dt
f (t )
d
(t )
t 0 t
dt
d
lim
(t )
t 0 t
dt
lim
9
10. Произвольные движения твёрдого тела
Пример:плоскопараллельное
движение
колеса
без
проскальзывания по горизонтальной поверхности. Качение колеса
можно представить как сумму двух движений: поступательного
движения со скоростью центра масс тела и вращения
относительно оси, проходящей через центр масс.
10
11. Динамика вращательного движения твёрдого тела
«Я ценю умение строить аналогии, которые, если они смелы иразумны, выводят нас за пределы того, что пожелала нам
открыть природа, позволяя предвидеть факты ещё до того, как
мы их увидим».
Ж. Л. Даламбер
ДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА
11
12. Основное уравнение динамики вращательного движения
ОСНОВНОЕ УРАВНЕНИЕДИНАМИКИ ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ
13. Динамика вращательного движения
Динамика поступательногоОсновная задача динамики
движения материальной точки
вращательного движения: Установить
оперирует такими понятиями, как
связь углового ускорения
сила, масса, импульс.
вращательного движения тела с
Ускорение поступательно
силовыми характеристиками его
движущегося тела зависит от
взаимодействия с другими телами и
действующей на тело силы
собственными свойствами
(суммы действующих сил) и массы
вращающегося тела.
тела (второй закон Ньютона):
a
F
m
13
14. Основное уравнение динамики вращательного движения
Для произвольной точки теламассой m
Для тела как совокупности
частиц малых масс
F Fn F
(m r m r ... m r ) M i M e
2
11
2
2 2
2
n n
Скалярная физическая величина,
характеризующая распределение
массы относительно оси вращения,
называется моментом инерции
тела:
По второму закону Ньютона
Fn man , F ma m r
С учётом векторного характера
Из геометрических соображений
F F sin F
d
,
r
mr Fd M
2
I m1r12 m2 r22 ... mn rn2 mi ri 2
Сумма моментов внутренних сил
Мi равна нулю, следовательно
I M e M
14
15. Экспериментальное изучение закономерностей вращательного движения
1.2.
3.
4.
Устройство и принцип действия прибора
Исследование зависимости углового ускорения вращения диска от
момента действующей силы:
от величины действующей силы F при неизменном значении
плеча силы относительно данной оси вращения d (d = const);
от плеча силы относительно данной оси вращения при
постоянной действующей силе (F = const);
от суммы моментов всех действующих на тело сил
относительно данной оси вращения.
Исследование зависимости углового ускорения от свойств
вращающегося тела:
от массы вращающегося тела при неизменном моменте сил;
от распределения массы относительно оси вращения при
неизменном моменте сил.
Результаты опытов:
M
I
15
16. Результаты выполненных экспериментов
Поступательное движениеМасса
Сила
m, m кг
F , F Н
Вращательное движение
Момент инерции
Момент силы
I kmr2 , I кг м 2
M Fd ; М , M Н м
Основное уравнение динамики
Основное уравнение динамики
a
F
m
Ускорение поступательно движущегося тела
прямо пропорционально сумме всех
действующих на него сил и обратно
пропорционально массе тела.
M
I
Угловое ускорение вращающегося тела
прямо пропорционально сумме моментов
всех действующих на него сил
относительно оси вращения тела и
обратно пропорционально моменту
инерции тела относительно этой оси
вращения.
Принципиальная разница: масса является инвариантом и не зависит от того,
как тело движется. Момент инерции изменяется при изменении положения
оси вращения или её направления в пространстве.
16
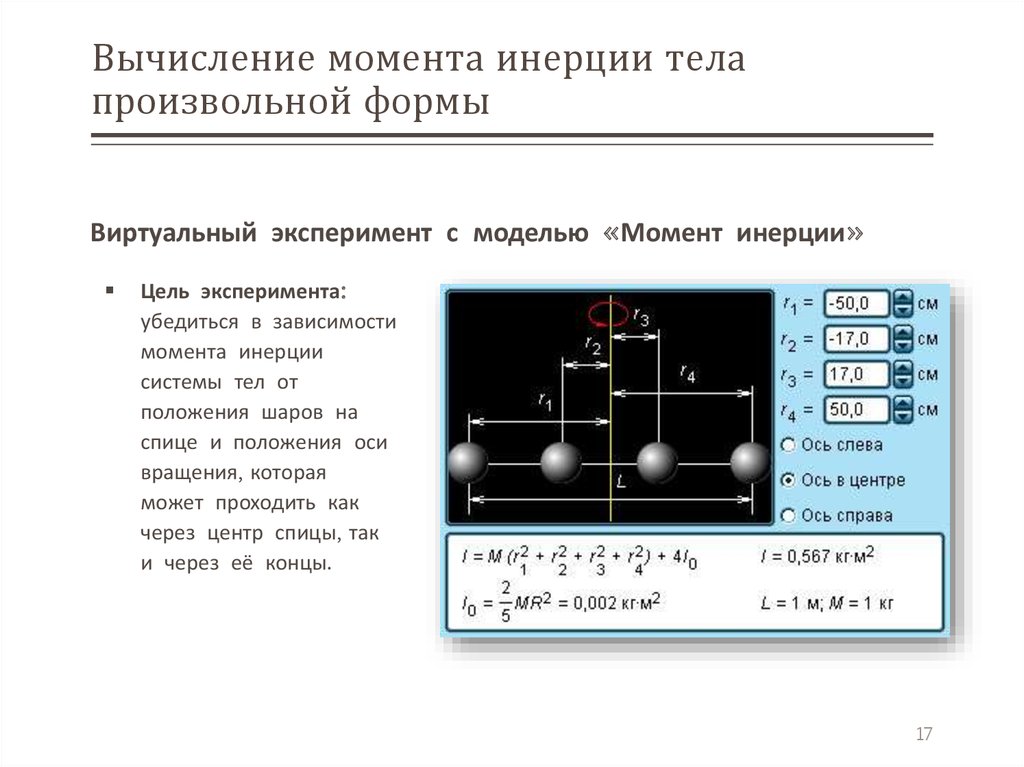
17. Вычисление момента инерции тела произвольной формы
Виртуальный эксперимент с моделью «Момент инерции»Цель эксперимента:
убедиться в зависимости
момента инерции
системы тел от
положения шаров на
спице и положения оси
вращения, которая
может проходить как
через центр спицы, так
и через её концы.
17
18.
Моменты инерции некоторых телШар
I
2 2
mr
5
Однородная
пластинка
I
1
m( a 2 b 2 )
12
Тонкостенная
сфера
I
2 2
mr
3
Сплошной
цилиндр
I
1 2
mr
2
Однородный
стержень
I
1
ml 2
12
Толстостенный
цилиндр
I
1
m(r12 r22 )
2
Диск
I
1 2
mr
2
Диск
I
1 2
mr
4
Тонкостенный
цилиндр
Произвольное
тело
I mr 2
I mi ri 2
18
19. Теорема Штейнера
Теорема о переносе осей инерции(Штейнера): момент инерции
твёрдого тела относительно
произвольной оси I равен сумме
момента инерции этого тела
I0 относительно оси, проходящей
через центр масс тела параллельно
рассматриваемой оси, и
произведения массы тела m на
квадрат расстояния d между осями:
Применение теоремы Штейнера.
Задание. Определить момент
инерции однородного стержня
длиной l относительно оси,
проходящей через один из его
концов перпендикулярно стержню.
Решение. Центр масс однородного
стержня расположен посредине,
поэтому момент инерции стержня
относительно оси, проходящей через
один из его концов, равен
2
1
l 1
I ml 2 m ml 2 .
12
3
2
I I 0 md 2
19
20. Динамика произвольного движения
ДИНАМИКАПРОИЗВОЛЬНОГО
ДВИЖЕНИЯ
21. Динамика произвольного движения
Произвольное движение твёрдого тела можно разложить на поступательноедвижение, в котором все точки тела движутся со скоростью центра масс тела, и
вращение вокруг центра масс.
Теорема о движении центра масс: центр масс
механической
системы
движется
как
материальная точка массой, равной массе
всей системы, к которой приложены все
внешние силы действующие на систему.
Следствия:
Если вектор внешних сил системы равен
нулю, то центр масс системы либо движется
с постоянной по величине и направлению
скоростью, либо находится в состоянии
покоя.
Если сумма проекций внешних сил на
какую-либо ось равна нулю, то проекция
вектора скорости движения центра масс
системы на эту ось либо постоянна, либо
равна нулю.
Внутренние силы не влияют на движение
центра масс.
21
22. Иллюстрация теоремы
Режимпоследовательной
съёмки позволяет
проиллюстрировать
теорему о движении
центра масс системы:
при спуске затвора за
одну секунду можно
запечатлеть несколько
изображений. При
объединении такой
серии спортсмены,
выполняющие трюки, и
животные в движении
превращаются в
плотную очередь
близнецов.
22
23. Изучение движения центра масс системы
Виртуальный эксперимент с моделью «Теорема о движениицентра масс»
Цель эксперимента:
изучить движение центра
масс системы из двух
осколков снаряда под
действием силы тяжести.
Убедиться в правомерности
применения теоремы о
движении центра масс к
описанию произвольных
движений на примере
баллистического движения,
изменяя его параметры: угол
выстрела, начальную скорость
снаряда и отношение масс
осколков.
23
24. Законы сохранения
«... аналогия является специфическим случаемсимметрии, особым видом единства сохранения и
изменения. Следовательно, использовать в анализе
метод аналогии, — значит действовать в соответствии с
принципом симметрии. Аналогия не только допустима,
но и необходима в познании природы вещей....»
Овчинников Н. Ф. Принципы сохранения
ЗАКОНЫ СОХРАНЕНИЯ
24
25. Закон сохранения момента импульса
ЗАКОН СОХРАНЕНИЯМОМЕНТА ИМПУЛЬСА
26. Аналогия математического описания
Поступательное движение Вращательное движениеИз основного уравнения динамики
поступательного движения
2 1
F ma m
t
F t m 2 m 1 (m ) p
кг м
p m ( р ), р
с
Произведение массы тела на
скорость его движения - импульс
тела.
В отсутствие действия сил импульс
тела сохраняется:
0 m 2 m 1 p, р const
Из основного уравнения динамики
вращательного движения
2 1
M I I
t
M t I 2 I 1 ( I ) L
кг м 2
L I ( L ), L
с
Произведение момента инерции
тела на угловую скорость его
вращения - момент импульса.
При равенстве нулю суммарного
момента сил
0 I 2 I 1 L, L const
26
27. Фундаментальный закон природы
Закон сохранения момента импульса - одиниз важнейших фундаментальных законов
природы - является следствием
изотропности пространства (симметрии
относительно поворотов в пространстве).
Закон сохранения момента импульса не
является следствием законов Ньютона.
Предложенный подход к выводу закона носит
частный характер.
При сходной алгебраической форме записи
законы сохранения импульса и момента
импульса в применении к одному телу
имеют разный смысл: в отличие от скорости
поступательного движения угловая скорость
вращения тела может меняться за счёт
изменения момента инерции тела I
внутренними силами.
Закон сохранения момента импульса
выполняется для любых физических систем и
процессов, не только механических.
27
28. Закон сохранения момента импульса
Момент импульса системы тел сохраняется неизменным при любыхвзаимодействиях внутри системы, если результирующий момент внешних
сил, действующих на неё, равен нулю.
При M 0
L I const
Следствия из закона сохранения момента импульса
в случае изменения скорости вращения одной части системы другая также
изменит скорость вращения, но в противоположную сторону таким образом,
что момент импульса системы не изменится;
если момент инерции замкнутой системы в процессе вращения изменяется,
то изменяется и её угловая скорость таким образом, что момент импульса
системы останется тем же самым
в случае, когда сумма моментов внешних сил относительно некоторой оси
равняется нулю, момент импульса системы относительно этой же оси
остается постоянным.
Экспериментальная проверка. Опыты со скамьёй Жуковского
Границы применимости. Закон сохранения момента импульса выполняется в
инерциальных системах отсчёта.
28
29. Скамья Жуковского
Особенности примененияЗакон сохранения момента импульса
выполняется, если:
1. сумма моментов внешних сил равна нулю
(силы при этом могут не
уравновешиваться);
2. тело движется в центральном силовом
поле (при отсутствии других внешних сил;
относительно центра поля)
Закон сохранения момента импульса
применяют:
1. когда характер изменения со временем
сил взаимодействия между частями
системы сложен или неизвестен;
2. относительно одной и той же оси для
всех моментов импульса и сил;
3. как к полностью, так и частично
изолированным системам.
31
30.
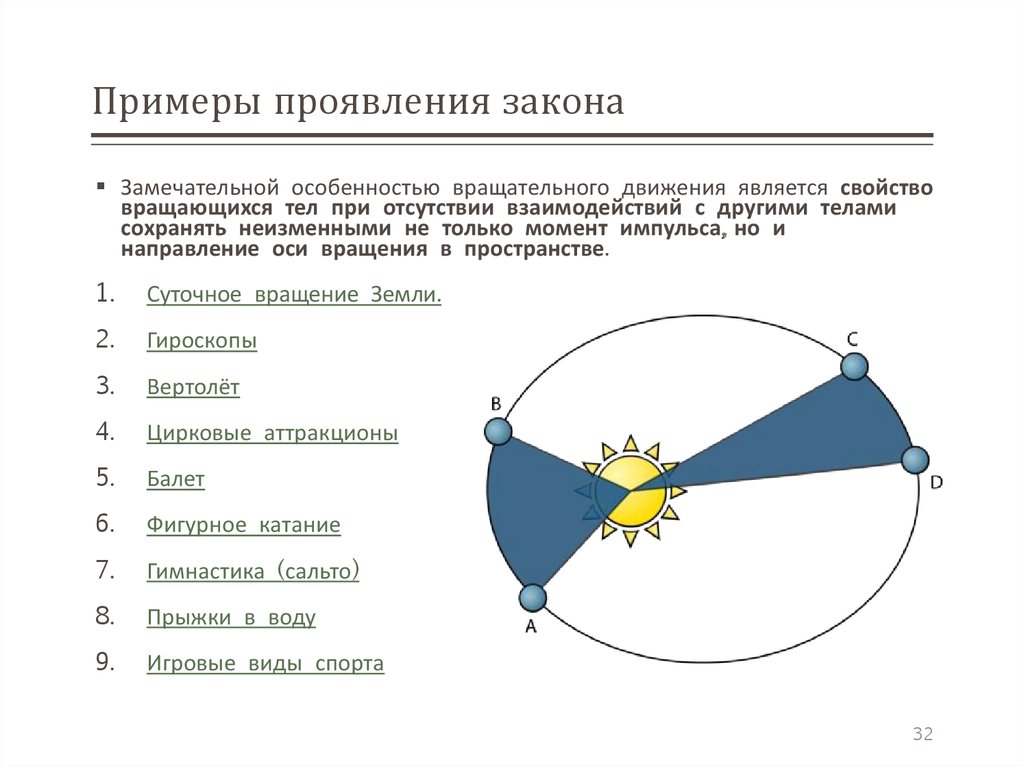
Примеры проявления законаЗамечательной особенностью вращательного движения является свойство
вращающихся тел при отсутствии взаимодействий с другими телами
сохранять неизменными не только момент импульса, но и
направление оси вращения в пространстве.
1.
Суточное вращение Земли.
2.
Гироскопы
3.
Вертолёт
4.
Цирковые аттракционы
5.
Балет
6.
Фигурное катание
7.
Гимнастика (сальто)
8.
Прыжки в воду
9.
Игровые виды спорта
32
31. Особенности применения
КИНЕТИЧЕСКАЯ ЭНЕРГИЯВРАЩАЮЩЕГОСЯ ТЕЛА
32. Примеры проявления закона
Кинетическая энергия вращающегося телаКинетическая энергия вращающегося тела равна сумме кинетических энергий
отдельных его частей:
mn n2
m1 12 m2 22
Ek
...
.
2
2
2
Поскольку угловые скорости всех точек вращающегося тела одинаковы, то,
используя связь линейной и угловой скоростей, получим:
mn 2 rn2 2
m1 2 r12 m2 2 r22
Ek
...
(m1r12 m2 r22 ... mn rn2 ).
2
2
2
2
Величина, стоящая в скобках, представляет собой момент инерции тела
относительно оси вращения:
I m1r12 m2 r22 ... mn rn2 .
Формула кинетической энергии вращающегося тела:
I 2
Еk
2
45
33. Пример 1. Суточное вращение Земли
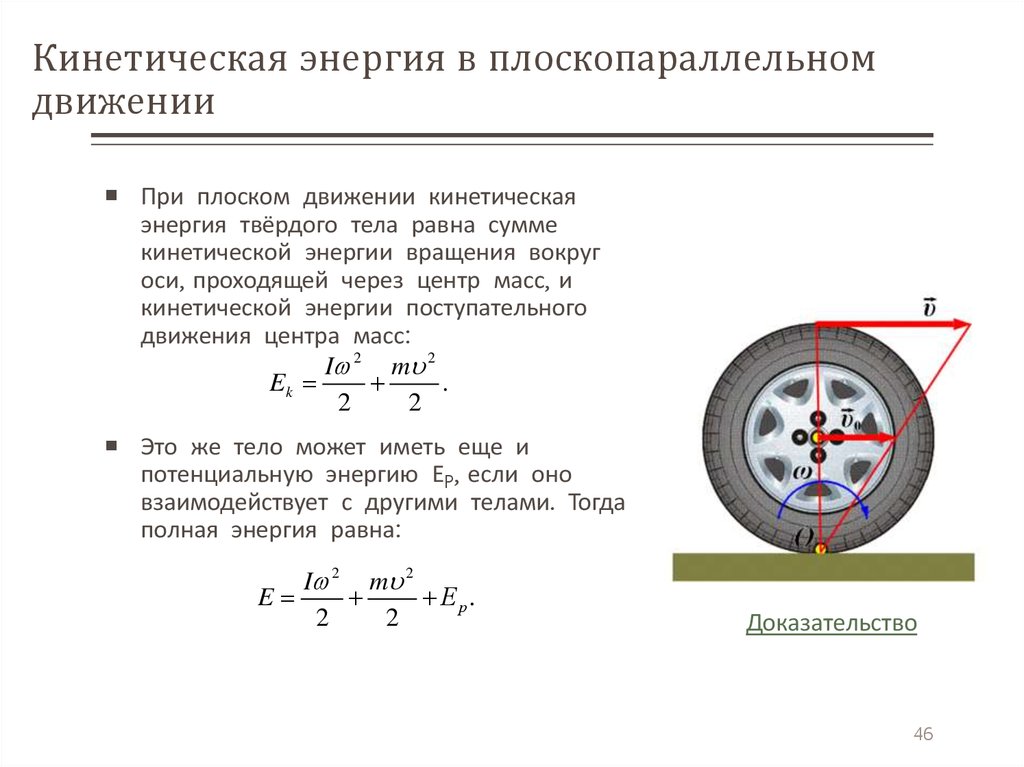
Кинетическая энергия в плоскопараллельномдвижении
При плоском движении кинетическая
энергия твёрдого тела равна сумме
кинетической энергии вращения вокруг
оси, проходящей через центр масс, и
кинетической энергии поступательного
движения центра масс:
I 2 m 2
Ek
.
2
2
Это же тело может иметь еще и
потенциальную энергию ЕP, если оно
взаимодействует с другими телами. Тогда
полная энергия равна:
I 2 m 2
E
Ер.
2
2
Доказательство
46
34. Пример 2. Гироскопы
Теорема КёнигаКинетическая энергия любой
системы материальных точек
равна сумме кинетической
энергии всей массы системы,
мысленно сосредоточенной в
ее центре масс и
движущейся вместе с ним, и
кинетической энергии всех
материальных точек той же
системы в их относительном
движении по отношению к
поступательно движущейся
системе координат с
началом в центре масс.
48
35. Применение гироскопов
ЗАКОН СОХРАНЕНИЯЭНЕРГИИ
36. Пример 3. Вертолёт
Закон сохранения энергииПревращение одного вида
механической энергии в другой на
примере маятника Максвелла:
Пример 1. Маятник Максвелла
m 2 I 2
mgh
.
2
2
Движение маятника
периодическое. Подобным
образом движется игрушка «йойо».
Вследствие трения маятник через
некоторое время остановится:
E1 Е2 Q
50
37. Пример 4. Цирковые аттракционы
Использование кинетической энергиивращения
Толкание ядра, метание молота, диска и других спортивных снарядов
требуют предварительного разгона для увеличения дальности полёта.
Увеличение скорости снаряда при отрыве от рук метателя (вылете),
достигается за счёт дополнительного вращения перед броском.
51
38. Пример 5. Балет
5239. Пример 6. Фигурное катание
Инерционные накопители энергииЗависимость кинетической энергии
вращения от момента инерции тел
используют в инерционных аккумуляторах.
Работа, совершаемая за счёт кинетической
энергии вращения, равна:
I 2
I
A
0 .
2
2
Примеры: гончарные
круги,
массивные
колёса водяных мельниц, маховики в
двигателях внутреннего сгорания. Маховики,
применяемые в прокатных станах, имеют
диаметр свыше трёх метров и массу более
сорока тонн.
2
53
40. Пример 7. Гимнастика
Ещё раз о скатыванииПо наклонной плоскости катятся без проскальзывания кольцо и диск, имеющие
одинаковую массу и диаметр. Почему кольцо и диск достигают конца
плоскости не одновременно? Ответ обоснуйте.
54
41. Пример 8. Прыжки в воду
«В физике часто случалось, что существенныйуспех был достигнут проведением
последовательной аналогии между не
связанными по виду явлениями».
Альберт Эйнштейн
ЗАКЛЮЧЕНИЕ
55
42. Проблема устойчивости вращения
Использованные информационныематериалы
Учебник для 10 класса с углублённым изучением физики под редакцией А.
А. Пинского, О. Ф. Кабардина. М. : «Просвещение», 2005.
Факультативный курс физики. О. Ф. Кабардин, В. А. Орлов, А. В. Пономарева.
М. : «Просвещение», 1977 г.
Ремизов А. Н. Курс физики: Учеб. для вузов / А. Н. Ремизов, А. Я. Потапенко.
М.: Дрофа, 2004.
Трофимова Т. И. Курс физики: Учеб. пособие для вузов. М.: Высшая школа,
1990.
http://ru.wikipedia.org/wiki/
http://elementy.ru/trefil/21152
http://www.physics.ru/courses/op25part1/content/chapter1/section/parag
raph23/theory.html
Physclips . Мультимедийное введение в физику.
http://www.animations.physics.unsw.edu.au/jw/rotation.htm и др.
В оформлении в учебных целях использованы иллюстративные материалы
сети Интернет.
56






































 physics
physics








