Similar presentations:
Движение абсолютно твёрдого тела. (Лекция 5)
1.
Движение абсолютнотвёрдого тела
1
2. Понятие абсолютно твёрдого тела
FF - внешняя сила
rjk
Δ m1
Δmi – элементарная масса
Δ m3
rjk – расстояние между точками j и k
Δ m2
Абсолютно твёрдое тело –
тело , расстояние между двумя любыми
точками которого во время движения
остаётся неизменным, т.е. тело не
деформируется
rjk = const
2
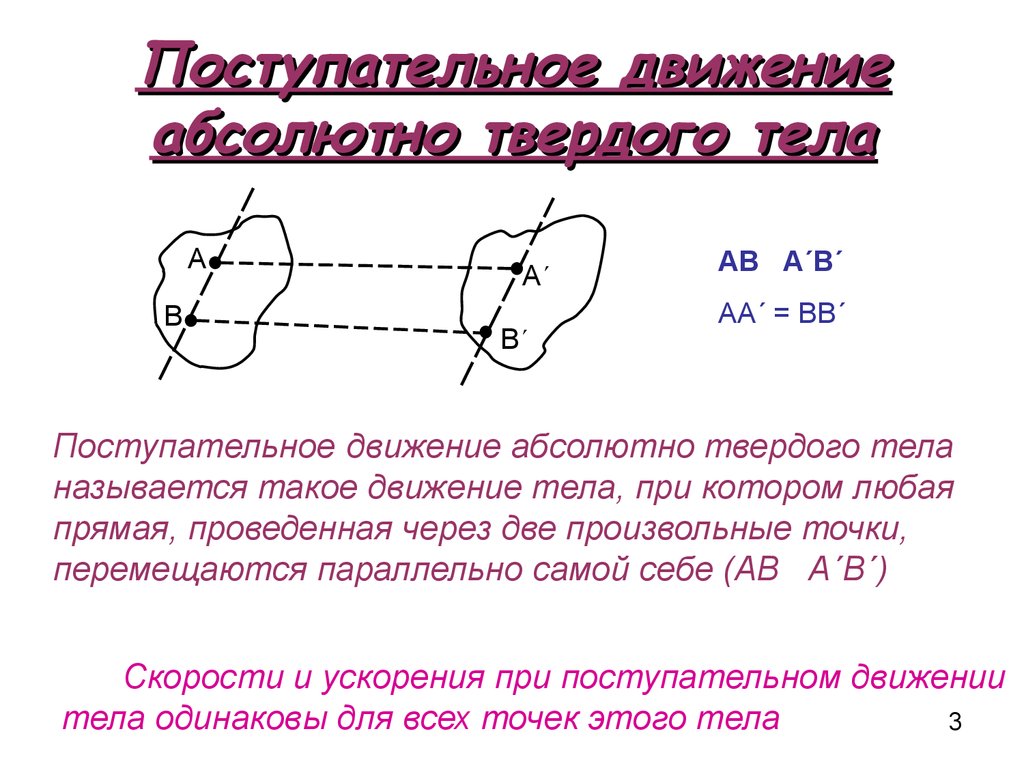
3. Поступательное движение абсолютно твердого тела
АВ
А´
В´
АВ А´В´
АА´ = ВВ´
Поступательное движение абсолютно твердого тела
называется такое движение тела, при котором любая
прямая, проведенная через две произвольные точки,
перемещаются параллельно самой себе (АВ А´В´)
Скорости и ускорения при поступательном движении
тела одинаковы для всех точек этого тела
3
4.
Закон движения центра масс телаm i Ч
a f i Fi
е
m i Ч
a е Fi е f i
i
i
fi 0
i
a mi Fi
i
i
m
i
a
- ускорение, одинаково для всех
точек тела
f i - внутренняя сила, действующая
на точку i со стороны других
точек
Fi
i
- внешняя сила, действующая
на точку i
m
i
Fi F
i
F=ma
m
F
- масса тела
- главный вектор внешних сил
Центр масс тела движется так, как движется материальная точка с
массой, равной массе тела m, под влиянием силы, равной
4
главному вектору внешних сил F
5.
Центром масс называется такая воображаемаяточка тела, радиус – вектор которой R, выражается
через радиусы векторы r1, r2… материальных точек
тела по формуле
m1r1 + m2r2 + …+ mNrN
R=
m
m = m1 + m2 + …+mN – общая масса тела, состоящего из
N материальных точек
5
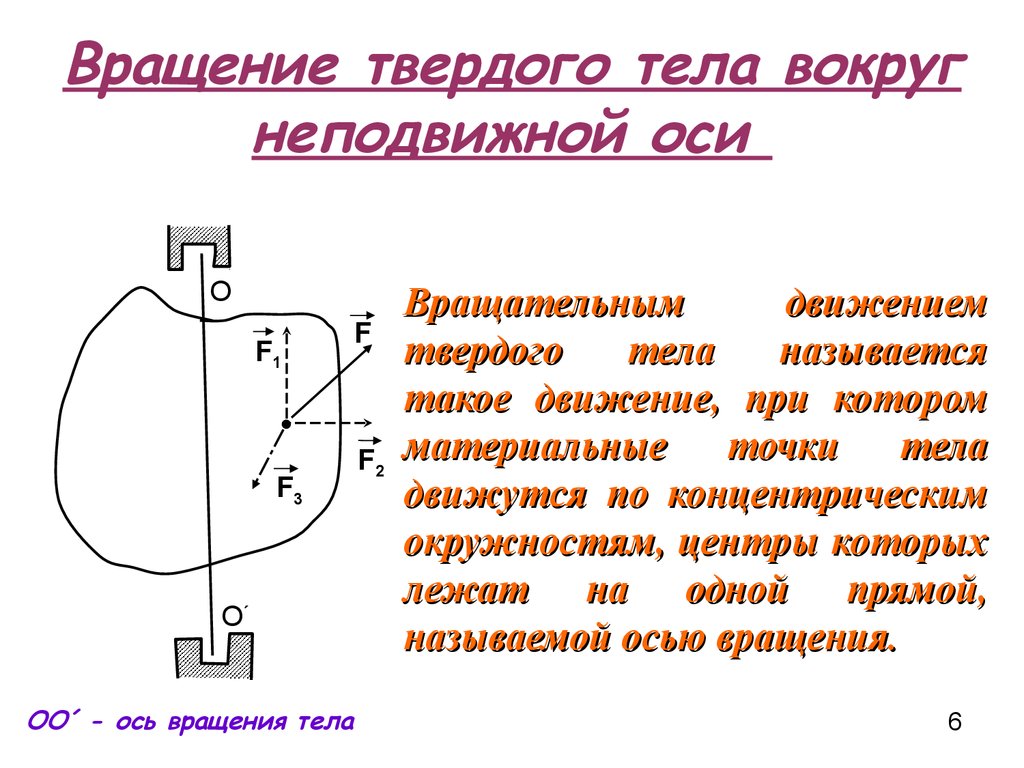
6. Вращение твердого тела вокруг неподвижной оси
ОF1
F3
О´
ОО´ - ось вращения тела
F
F2
Вращательным
движением
твердого
тела
называется
такое движение, при котором
материальные
точки
тела
движутся по концентрическим
окружностям, центры которых
лежат на одной прямой,
называемой осью вращения.
6
7. Момент силы относительно точки
- линия действия силыМ
ℓ
О
+ r
Произвольная
О
точка на оси
вращения
М = [r · F]
r ·sin = ℓ - плечо силы
α
F
М = r· F· sin = ℓ·F
M = ℓ·F
Момент силы относительно оси
О
F1
F
Вращение тела вызывается составляющей
F3, перпендикулярной плоскости, в которой
лежит ось вращения
ℓ
F2
F3
M = ℓ·F3
Модуль
момента
силы
относительно оси ОО´
О`
7
8. Основное уравнение динамики вращательного движения
Fi =Δm
i
r ∙Fi·a
=Δm
∙ ∙
i
i
i
rMi2 =I ∙
i
i
M1+M2+…=J1 +J2 +
…
M=J
Основное уравнение
вращательного
движения твердого
ai =
ri= =cons
i
t
Δmi∙ri2=Ji – момент
инерции
материальной точки
относительно оси
вращения
J +J +…=J –
1
2
момент инерции
тела
относительно оси
8
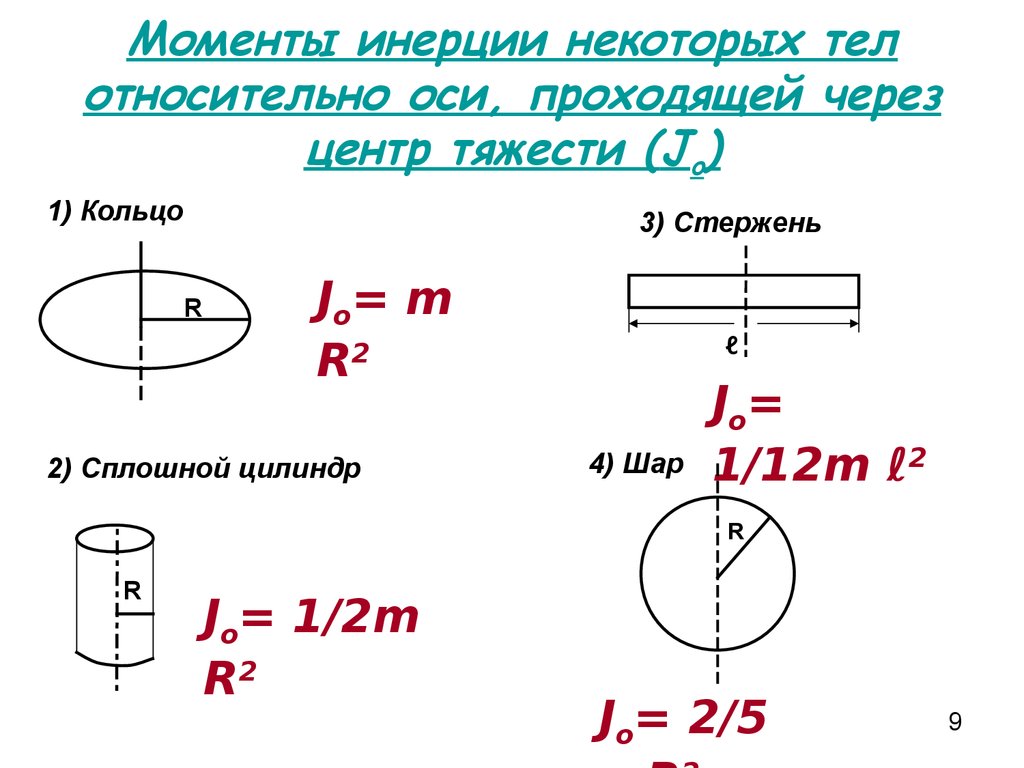
9. Моменты инерции некоторых тел относительно оси, проходящей через центр тяжести (Jo)
1) Кольцо3) Стержень
R
Jo= m
R2
2) Сплошной цилиндр
ℓ
4) Шар
Jo=
1/12m ℓ2
R
R
Jo= 1/2m
R2
Jo= 2/5
9
10. Работа и энергия вращательного движения твёрдого тела
При поступательном движенииРабота :
При вращательном движении
A = M · dφ
A=F·d S
Кинетическая
энергия:
1
Ек = m
2
J ω2
Ек =
2
Если тело вращается и движется поступательно:
m J ω2
Ек = 2 + 2
(Пример: движение колеса по дороге)
10
11. МОМЕНТ ИМПУЛЬСА ТЕЛА
M=J·ε- основное уравнение вращательного
движения твёрдого тела
М – момент силы, J – момент инерции,
dω
- угловое ускорение
ε =
dt
dω
; M · d t = J · d ω;
М = J ·
dt
М · d t = d (J ω) - если ось вращения не изменяет своего
положения
L = J ω – момент импульса тела, или интеграл движения
М·dt
– импульс
момента внешних сил
Импульс момента внешних сил, действующих на
тело, равен изменению момента импульса тела. 11
12. Закон сохранения момента импульса
Если система замкнутая, то внешниедействуют, и момент внешних сил М = 0.
M · dt = d(J·ω);
d(J·ω) = 0;
J·ω = L
силы
не
момент импульса
J·ω = const
Если система замкнутая, то момент импульса
системы сохраняется.
Сохраняется не только величина момента импульса, но и
направление.
Если J – уменьшается, то ω – увеличивается и наоборот.
12









 physics
physics








