Абсолютно твёрдое тело

1. Физические основы механики

Семестр 1

2.

Лекция № 6
1. Модель абсолютно твёрдого тела.
2. Кинематика движения свободного тела.
Вектор угловой скорости. Мгновенная ось
вращения.
3. Момент импульса частицы, момент
силы относительно точки и оси. Уравнения
моментов относительно точки и оси для
частицы и системы частиц.
4. Закон сохранения момента импульса.
Орбитальный
и
собственный
момент
импульса тела. Спин элементарных частиц.
5. Вращение твердого тела вокруг
неподвижной оси.
6. Момент инерции относительно оси. Теорема Гюйгенса-Штейнера.

3.

Абсолютно твёрдое тело - это система
материальных точек, где все расстояния между
ними сохраняются постоянными независимо от
внешних воздействий. Иными словами,
отсутствует относительное движение частиц.
Для полного и однозначного определения
положения тела в трёхмерном пространстве
необходимо задать 6 скалярных параметров:
три координаты центра масс тела и три угла,
фиксирующие ориентацию тела. Число
независимых скалярных параметров, полностью
и однозначно определяющих положение системы
в пространстве, называется числом степеней
свободы. Частица имеет три степени свободы,
абсолютно твёрдое тело - шесть, а система из
n частиц - 3n степеней свободы.

4.

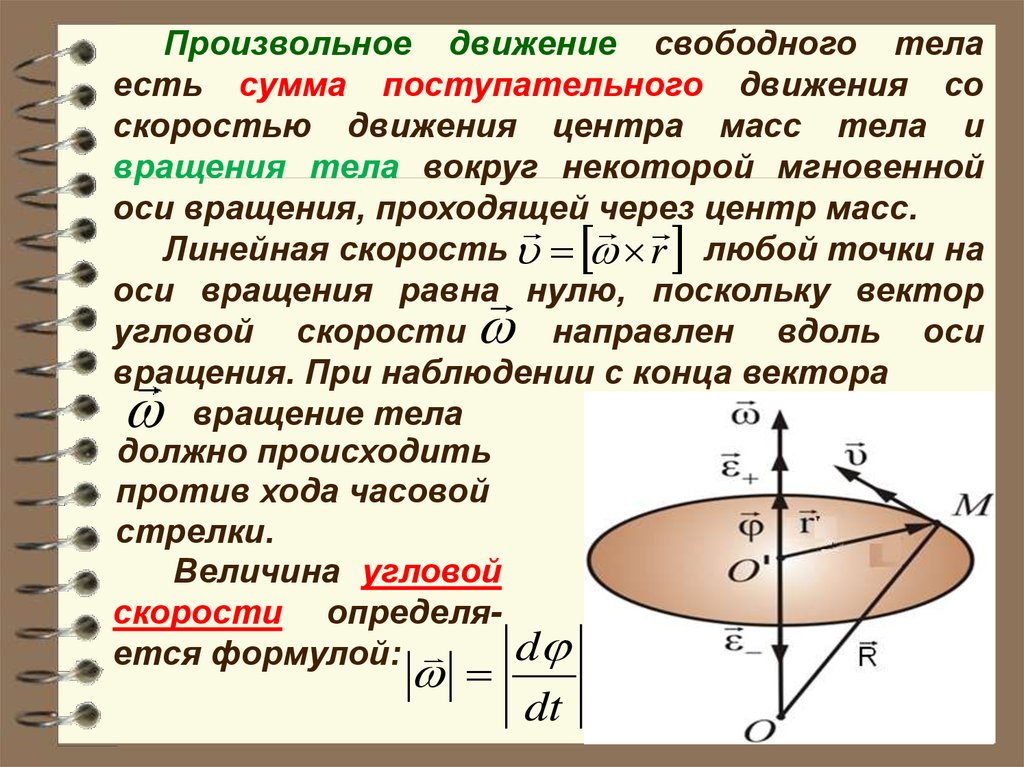
Произвольное движение свободного тела
есть сумма поступательного движения со
скоростью движения центра масс тела и
вращения тела вокруг некоторой мгновенной
оси вращения, проходящей через центр масс.
Линейная скорость r любой точки на
оси вращения равна нулю, поскольку вектор
угловой скорости
направлен вдоль оси
вращения. При наблюдении с конца вектора
вращение тела
должно происходить
против хода часовой
стрелки.
Величина угловой
скорости определяd
ется формулой:
dt

5.

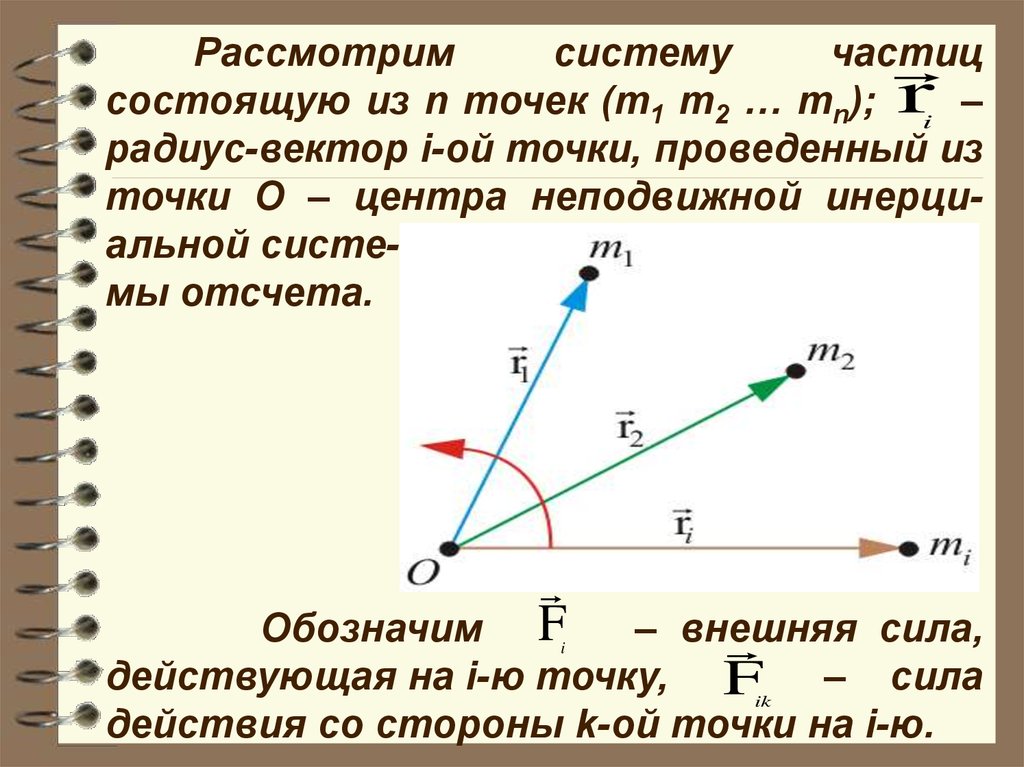
Рассмотрим
систему
частиц
состоящую из n точек (m1 m2 … mn); ri –
радиус-вектор i-ой точки, проведенный из
точки О – центра неподвижной инерциальной системы отсчета.
F
Обозначим
– внешняя
сила,
i
действующая на i-ю точку, Fik – сила
действия со стороны k-ой точки на i-ю.

6.

Запишем основное уравнение динамики
n
для точки: d
dt
m F F .
i
i
k 1
k i
ik
i
Умножим обе части векторно на
r
i
d
ri mi i ri Fik ri Fi .
k
dt
Знак производной можно вынести за
знак векторного произведения (и знак
суммы тоже), тогда:
d
ri mi i ri Fik ri Fi .
dt
k

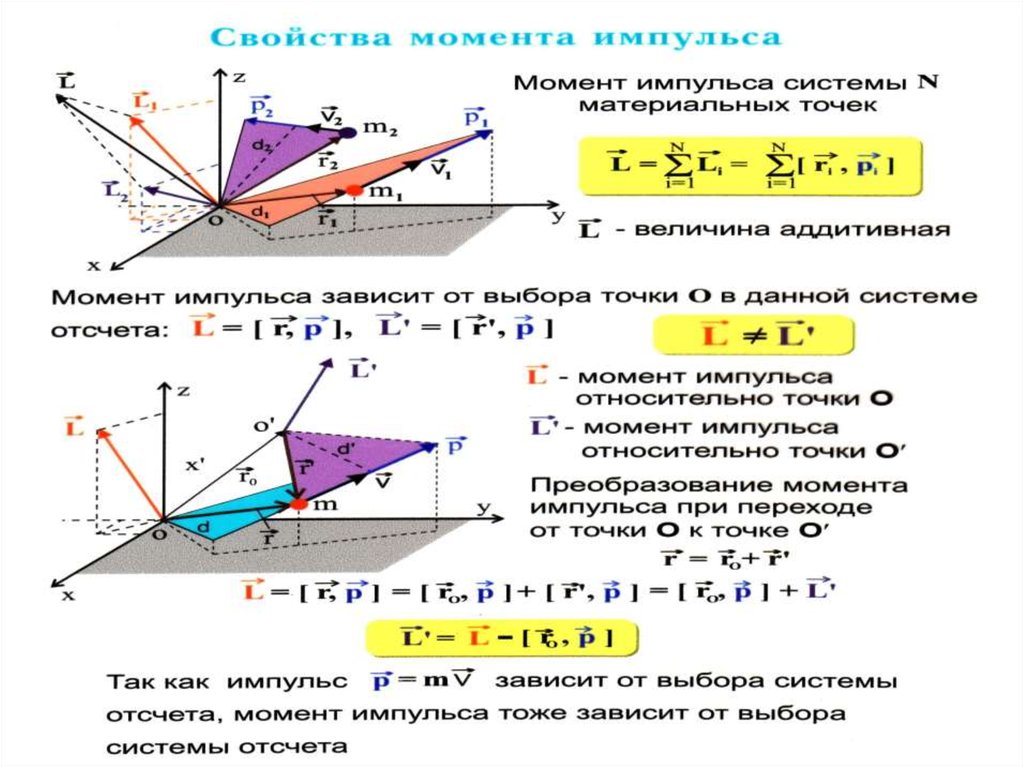
7.

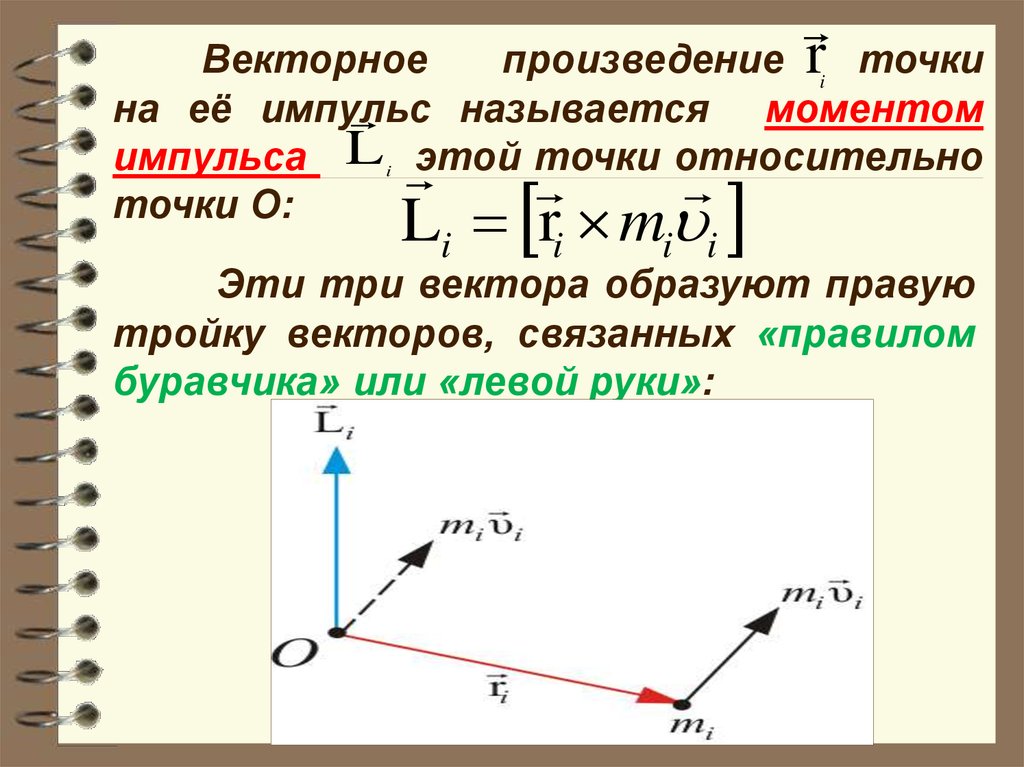
r
Векторное
произведение i точки
на её импульс
называется моментом
импульса L этой точки относительно
точки О:
i
Li ri mi i
Эти три вектора образуют правую
тройку векторов, связанных «правилом
буравчика» или «левой руки»:

8.

Li ri mi i .
Или L r р .
i j k
L x y z r p r , p .
рx р y рz
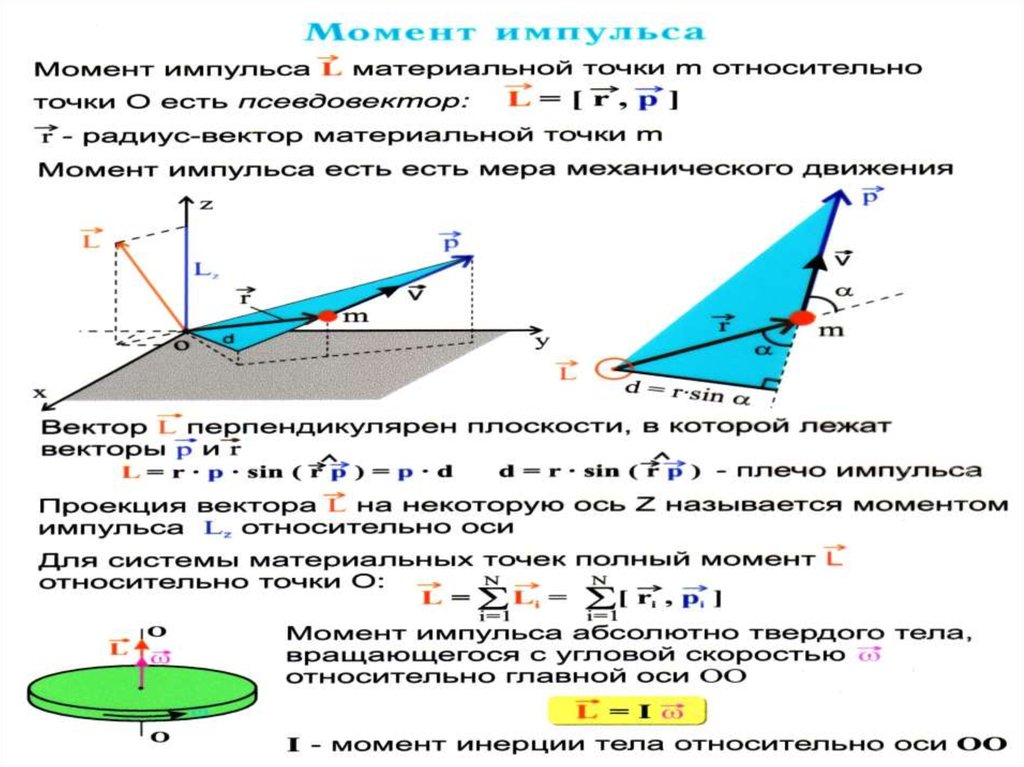
Модуль
L r p sin
Здесь L трехмерный момент импульса относительно центра
вращения О.

9.

10.

11.

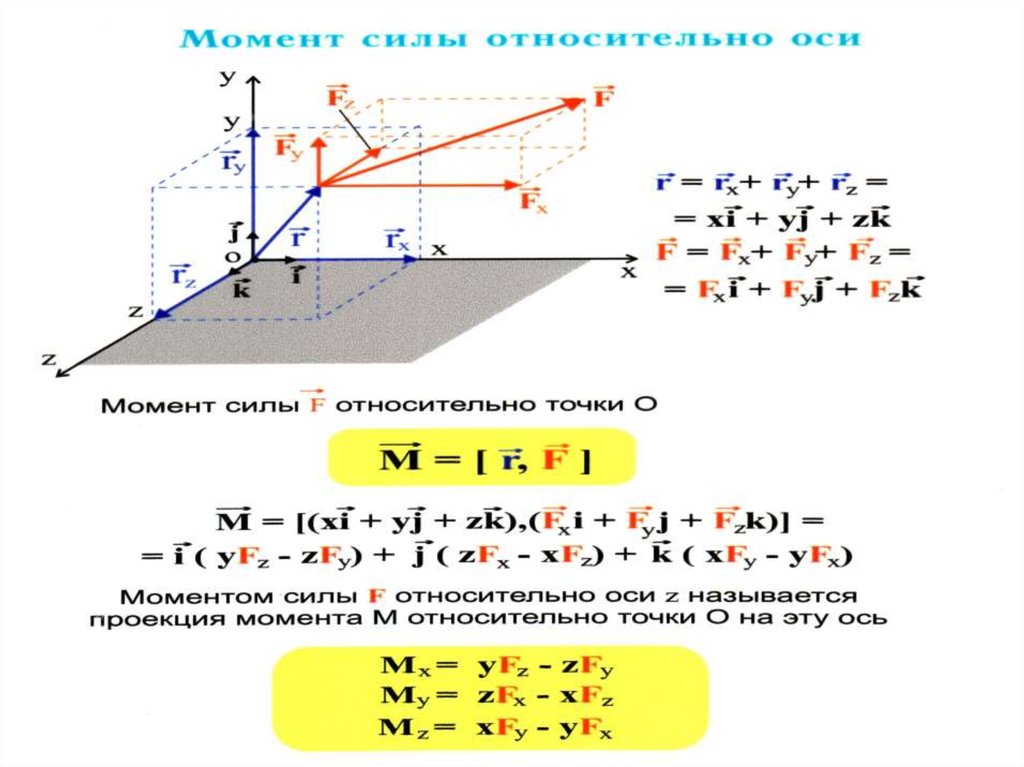
r
Векторное
произведение i
проведенного в точку приложения сил, на
эту силу называется моментом силы M :
Mi [ ri Fi ]
Обозначим li – плечо силы Fi,
Модуль момента силы:
M i Fi ri sin Fi li ,
li ri sin
- плечо
силы.
i

12.

13.

14.

C учетом новых обозначений:
dL
M M
dt
n
i
ik
k 1
i
Запишем систему n уравнений для всех
точек системы и сложим, левые и правые части
уравнений:
dL
M M .
dt
то
Так как F F
M 0.
n
n
n
i 1
k 1
n
i
i 1
ik
ki
ik
i
i 1
n
n
i 1
k 1
ik

15.

Здесь
сумма
производной суммы:
производных
равна
dL
dL
,
dt
dt
n
i
i 1
M
где L – момент
импульса системы,
– результирующий момент всех внешних
сил относительно точки О.
Окончательно
получим
для
одной
материальной точки уравнение моментов
имеет вид
i
i
Mi
dL
M
dt
где
- момент всех сил действующих
на материальную точку

16.

Для системы материальных точек
уравнение моментов (относительно точки)
имеет вид:
внеш
M
dL
M
dt
внеш
где
-момент
всех
внешних
сил
действующих на систему относительно
точки O.
Проведём через точку O произвольную
неподвижную ось Z. Проекция векторного
уравнения моментов на ось Z -есть уравнение
моментов относительно данной оси:
dL z
M внеш
z
dt

17.

Для замкнутой системы тел момент
внешних сил всегда равен нулю, так как внешние
силы вообще не действуют на замкнутую
систему. Тогда:
и
dL внеш
M
0
dt
L const
Закон сохранения момента импульса –
момент импульса замкнутой системы тел
относительно любой неподвижной точки не
изменяется с течением времени.

18.

Аналогично для замкнутой системы частиц
вращающихся вокруг оси Z :
dL z
внеш
M z 0,
dt
отсюда
L z const
Если момент внешних сил относительно
неподвижной оси вращения тождественно равен
нулю, то момент импульса относительно этой
оси не изменяется в процессе движения.
Момент импульса и для незамкнутых
систем постоянен, если результирующий
момент внешних сил, приложенных к системе,
равен нулю.

19.

20.

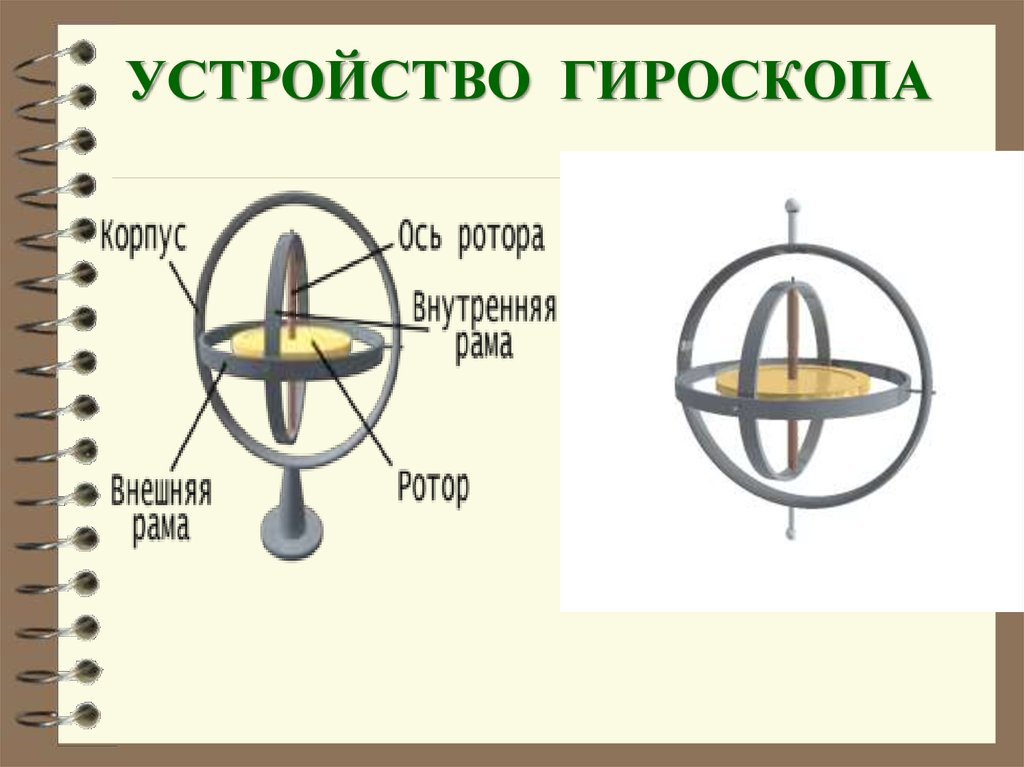
Уравновешенный гироскоп – быстро
вращающееся тело, имеющее три степени свободы
Используется гироскоп в различных
навигационных
устройствах
кораблей,
самолетов, ракет ( гирокомпас, гирогоризонт ).

21.

УСТРОЙСТВО ГИРОСКОПА

22.

ГИРОКОМПАС
Гироскопическим компасом (гирокомпасом)
называется гироскоп, ось которого может
свободно поворачиваться в горизонтальной
плоскости под влиянием суточного
вращения Земли.

23.

В классической механике полный момент
импульса тела относительно неподвижной точки
можно всегда рассматривать как сумму двух
моментов импульса:
L0 L0орб. L0 соб.
где L0орб. - орбитальный момент импульса,
связанный с движением центра масс тела
относительно
точки О,
L0соб. - собственный момент импульса тела
относительно его центра масс
Согласно
законам
квантовой
механики
элементарные частицы могут обладать
орбитальным
и
собственным
моментом
импульса, который называют спином. Спин не
связан с вращением частицы как целого вокруг
оси, проходящей через центр масс частицы.
Спин частицы измеряется в единицах , где

24. УСТРОЙСТВО ГИРОСКОПА

h 2 и
h= 6,62·10-34Дж·с - постоянная Планка,
и равен S
S -целое(в т.ч. нулевое) положительное число
для бозонов или полуцелое положительное
-и
число для фермионов. Спин
- мезонов
равен 0, спин электрона, протона, нейтрона и
нейтрино равен 1 2 , спин фотона равен 1 и спин
гравитона (кванта гравитационного поля) равен
2.
Существование закона сохранения момента
импульса вытекает из изотропности
пространства, свойства которого не зависят
от выбора направления наблюдения.

25. ГИРОКОМПАС

Динамика вращательного движения
твердого тела относительно оси
Описанное нами движение твердого тела
относительно неподвижной точки является
основным видом
движения. Однако вычислить
вектор
L - момент импульса системы
относительно произвольной точки не просто:
надо знать шесть проекций (три задают
положение тела, три задают положение точки).
Значительно проще найти момент импульса
L тела, вращающегося вокруг неподвижной
оси (z) .

26.

Пусть некоторое тело вращается
вокруг оси z . Получим уравнение
динамики для некоторой точки mi
этого тела находящегося на расстоянии Ri от оси
При этом
вращения.
помним, что L iz и M iz направлены
вдоль оси вращения z, поэтому в
дальнейшем опустим значок z.
всегда
dL
M
dt
или
i
i
d
[R i mi i ] M i
dt

27.

Так как у всех
точек
i
разная, введем, ω вектор угловой скорости
причем ω i / Ri
Тогда
d
m R ω M
dt
2
i
i
i
Так как тело абсолютно твердое, то в
процессе вращения mi и Ri останутся
неизменными. Тогда:
dω
mR
i
i
2
dt
M.
i

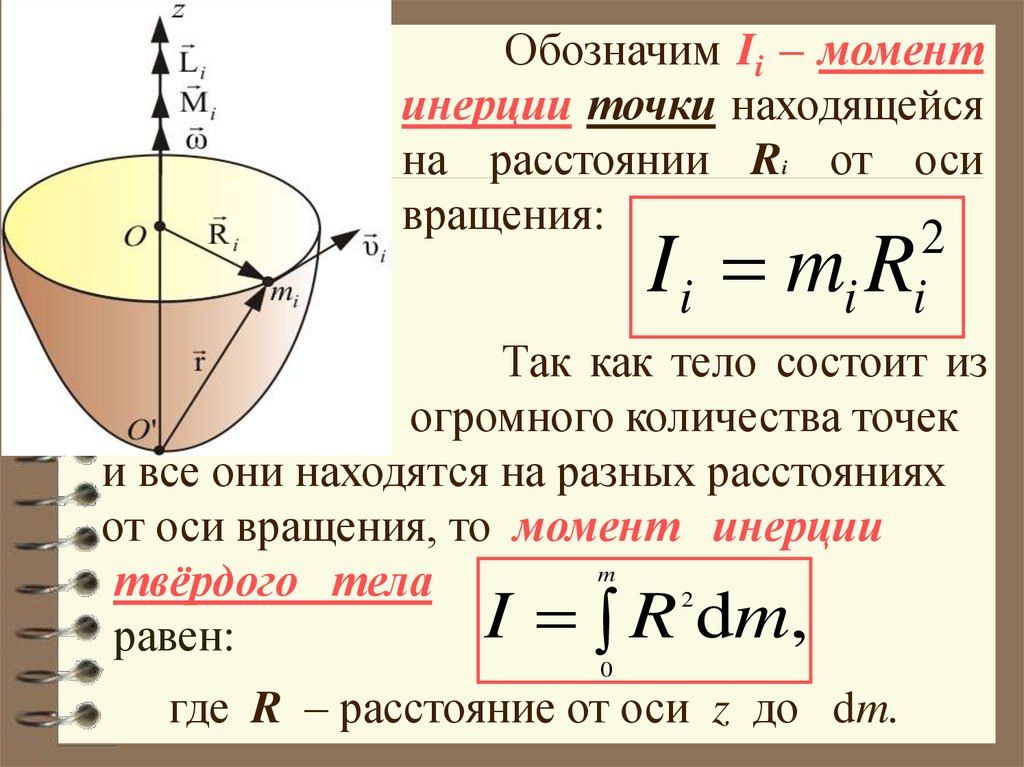
28. Динамика вращательного движения твердого тела относительно оси

Обозначим Ii – момент
инерции точки находящейся
на расстоянии Ri от оси
вращения:
I i mi R
2
i
Так как тело состоит из
огромного количества точек
и все они находятся на разных расстояниях
от оси вращения, то момент инерции
m
твёрдого тела
2
I R dm,
равен:
0
где R – расстояние от оси z до dm.

29.

Просуммировав по всем i-ым
точкам,
dω
I
получим
или
dt
M
I ε M
Это основное уравнение динамики
тела вращающегося вокруг неподвижной
оси. (Сравним:
ma F –
основное
уравнение
динамики
поступательного движения тела).
Idω Mdt ;
Idω dL

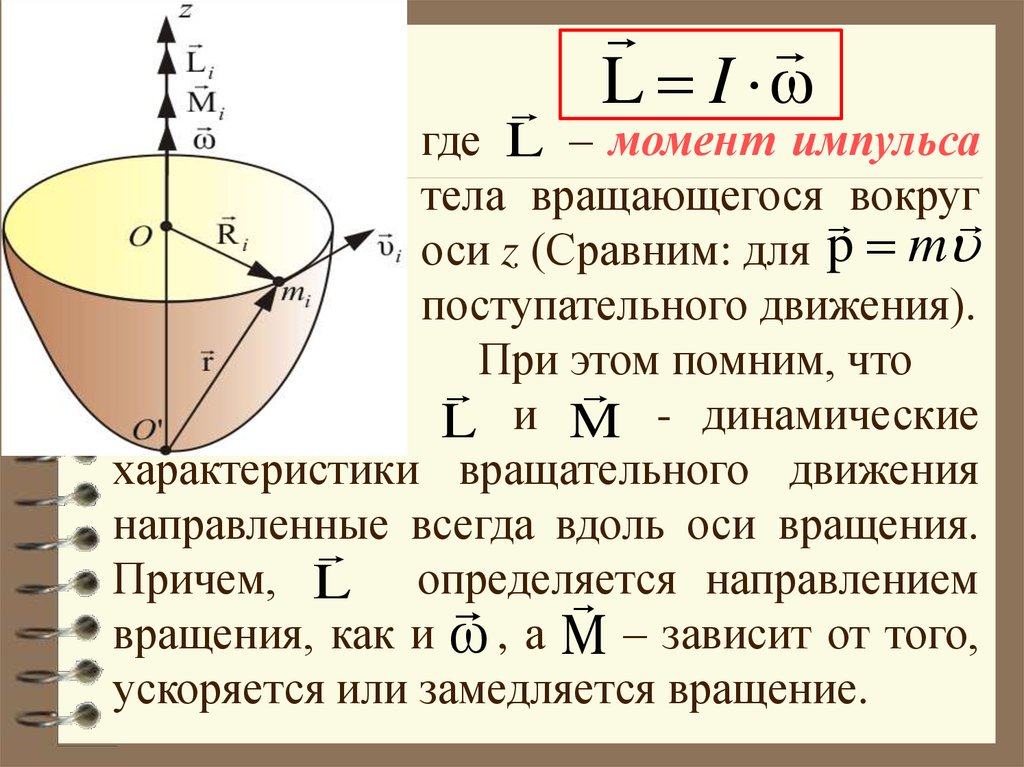
30.

L I ω
где L – момент импульса
тела вращающегося вокруг
оси z (Сравним: для p m
поступательного движения).
При этом помним, что
L и M - динамические
характеристики вращательного движения
направленные
всегда
вдоль
оси
вращения.
Причем, L определяется
направлением
вращения, как и ω , а M – зависит от того,
ускоряется или замедляется вращение.

31.

Повторим основные характеристики
вращательного движения
Эти формулы получены для
Li I i z Момент импульса
одной точки вращающегося
твердого тела
M i I i z Момент силы
Суммируя по всему телу,
получим
I i z mi ri 2 Момент инерции
n
Lz Li I z Момент импульса
твердого тела
i 1
M z M i I z
n
i 1
n
I z Ii z
i 1
Момент силы
твердого тела
Момент инерции
твердого тела
Основной закон динамики вращательного движения
твердого тела
Z
Li|z
ω
K
ri
Mi

32.

Расчет моментов инерции
некоторых простых тел.
m
По формуле I R 2 dm не всегда
0
просто удается рассчитать
момент инерции
тел произвольной формы.
Наиболее легко эта задача решается
для тел простых форм, вращающихся
вокруг оси, проходящей через центр
инерции (центр масс) тела Ic.
В этом случае Ic вычисляется по
формуле:
2
I kmR
c

33.

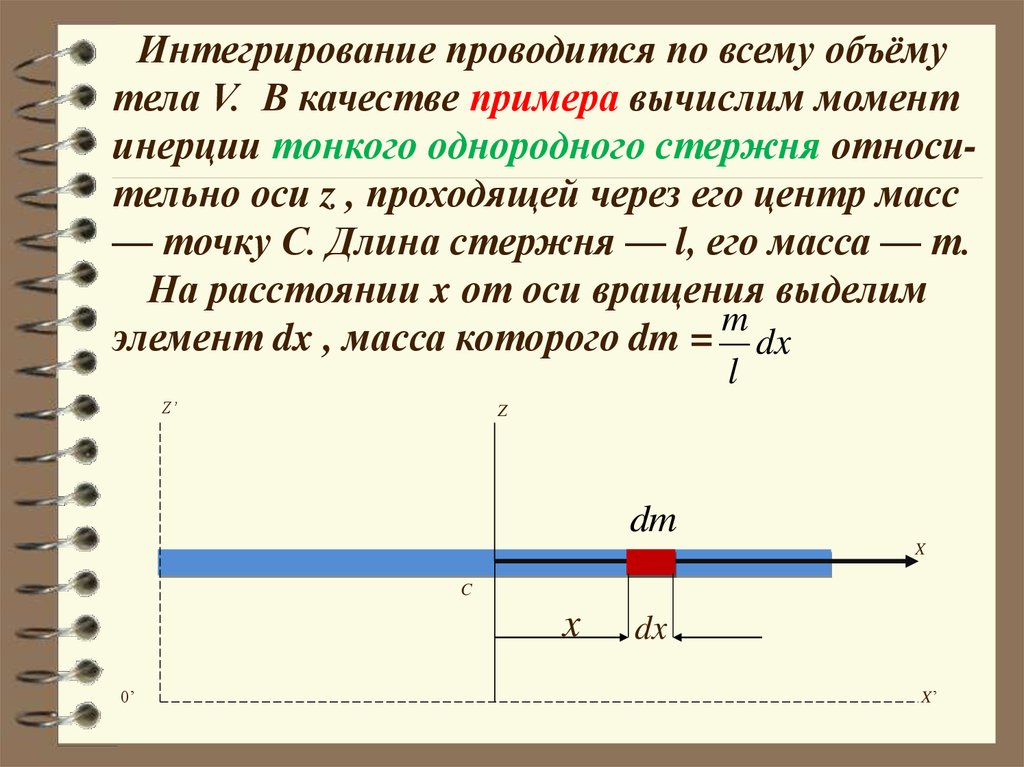
Интегрирование проводится по всему объёму
тела V. В качестве примера вычислим момент
инерции тонкого однородного стержня относительно оси z , проходящей через его центр масс
— точку С. Длина стержня — l, его масса — т.
На расстоянии x от оси вращения выделим
элемент dx , масса которого dm = m dx
l
Z’
Z
dm
X
C
x
0’
dx
X’

34. Повторим основные характеристики вращательного движения

Момент инерции этой частицы стержня равен:
m
2
dI z dm x dx x 2 . Вычислив подобным образом, моменты инерцииlвсех элементов стержня, сложим их, а в
пределе проинтегрируем:
l
.
Iz
2
l
2
l
т 2
т
тx
2
x dx x dx
l
l l
l 3
Таким образом:
3
2
2
l
2
l
2
т l 3 l 3 тl 2
3l 8 8 12
ml 2
Iz =
12
Как изменится момент инерции этого стержня, если
ось вращения перенести в другое место? Провести её,
например, через край стержня?
В этом случае прежний интеграл нужно рассмотреть в
l
3 l
2
т
т
x
тl
пределах от 0 до l:
2
I z
0
l
x dx
l 3
0
3

35. Расчет моментов инерции некоторых простых тел.

Моменты инерции шара, сферы, диска,
обруча и стержня.
Шар
Стержень
Диск
1
k 2 5;
k
k 1 2;
2
12
I 2 5 m R ; Ic 1 2 m R ;
1
2
c
Сфера
Обруч
I 2 3 m R ; I m R
2
c
I
c
c
2
12
ml
2

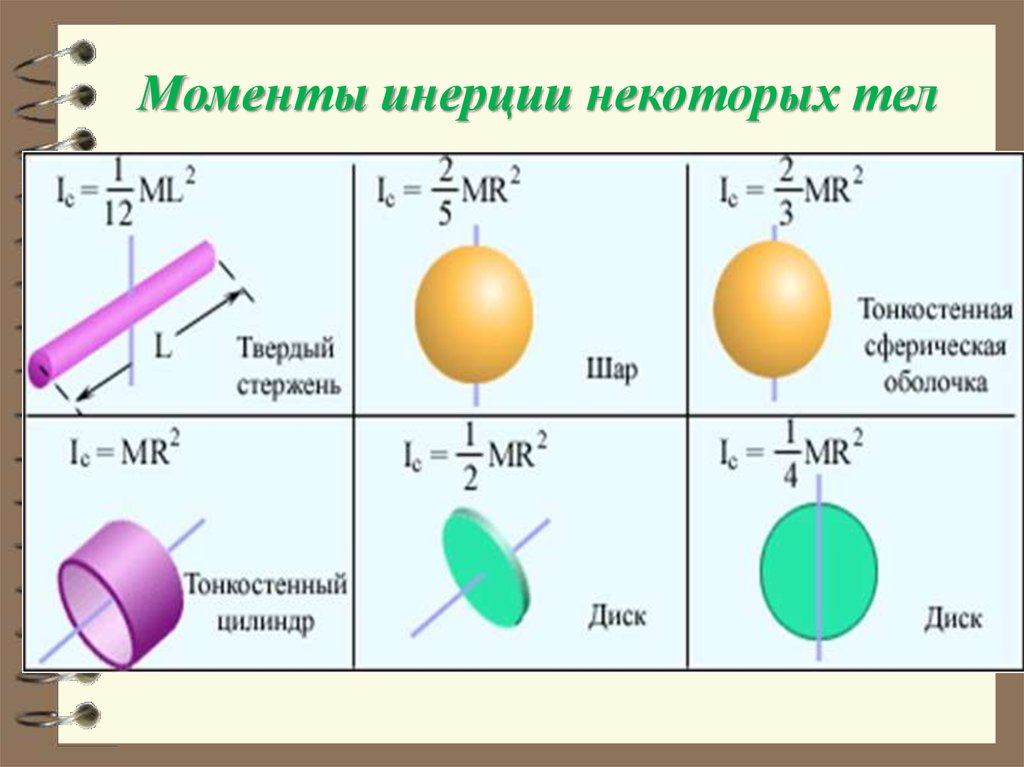
36.

Моменты инерции некоторых тел

37.

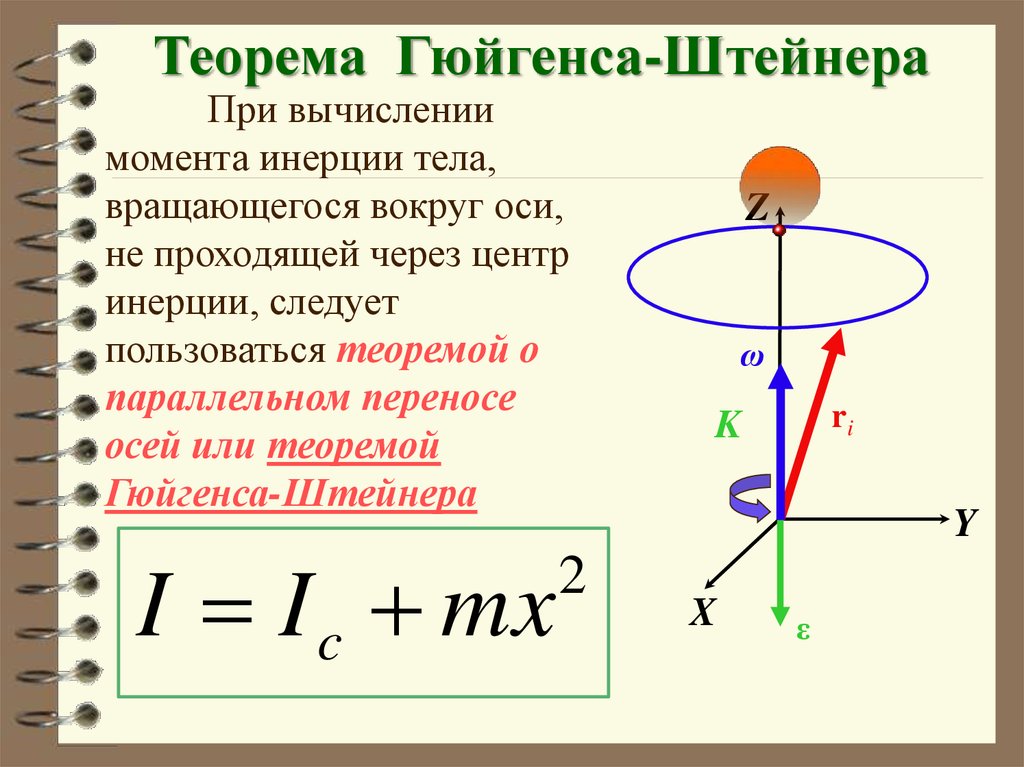
Теорема Гюйгенса-Штейнера
При вычислении
момента инерции тела,
вращающегося вокруг оси,
не проходящей через центр
инерции, следует
пользоваться теоремой о
параллельном переносе
осей или теоремой
Гюйгенса-Штейнера
I I c mx
2
Z
ω
ri
K
Y
X
ε

38.

Теорема Гюйгенса-Штейнера: Момент
инерции тела относительно произвольной оси I
равен сумме момента инерции Ic относительно
оси, параллельной данной и проходящей через
центр масс тела, и произведения массы тела т
на квадрат расстояния между осями:
O'
I = Ic + тx2,
o
x
где x — расстояние между
т
осями.

39.

Пример: стержень массой
m, длиной l, вращается
вокруг оси, проходящей
через конец стержня .
1
2
I c ml
12
2
1 2 1 2 1 2
l
I z I c m ml ml ml
4
3
2 12

40.

41.

ЛЕКЦИЯ ЗАКОНЧЕНА!