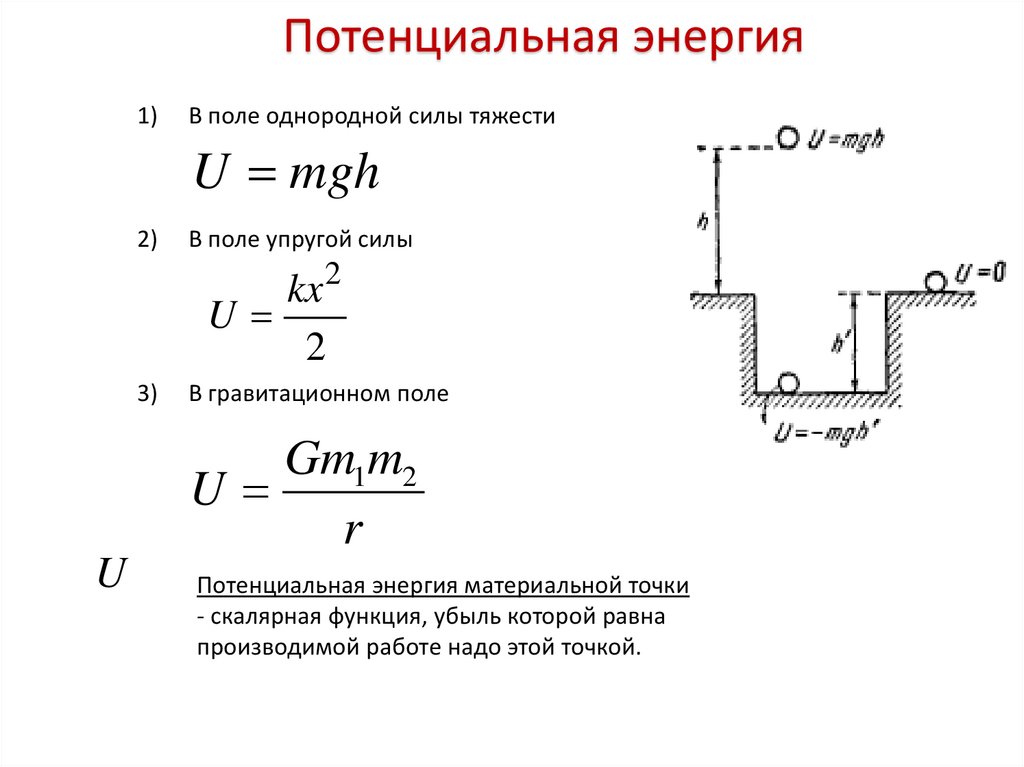
Потенциальная энергия

1. Механика 3

2.

Потенциальная энергия
1)
В поле однородной силы тяжести
U mgh
2)
В поле упругой силы
2
kx
U
2
3)
В гравитационном поле
Gm1m2
U
r
U
Потенциальная энергия материальной точки
- скалярная функция, убыль которой равна
производимой работе надо этой точкой.

3.

Взаимосвязь силы и потенциальной
энергии материальной точки
A U dA dU Fs ds
U
Fs
s
Из определения работы
U
Fx
x
U U U
F
i
j
k
y
z
x
i j k
x y
z
F U gradU
По оси x
По трем осям
Определение оператора набла
Сила через потенциальную энергию

4. Закон сохранения энергии

Уравнения Ньютона для N материальных точек
m1 v1 F1 F1
m2 v 2 F2 F2
. . . . . . . . . . . . . ....
mN v N FN FN
F1 , F2 ..FN
F1 , F2 ..FN
-равнодействующие внутренних консервативных cил
-равнодействующие внешних консервативных сил

5. Закон сохранения энергии

dv 1
( F1 F1 ) 0
dt
dv 2
( F2 F2 ) 0
m2
dt
. . . . . . . . . . . . . ....
dv N
( FN FN ) 0
mN
dt
m1
d r1 v1dt
d r2 v 2 dt
. . . . . . ....
d rN v N dt
m1 ( v1dv1 ) ( F1 F1 )d r1 0
m2 ( v 2 dv 2 ) ( F2 F2 ) d r2 0
. . . . . . . . . . . . . ....
mN ( v N dv N ) ( FN FN ) d rN 0

6. Закон сохранения энергии

m1 ( v1dv1 ) ( F1 F1 )d r1 0
m2 ( v 2 dv 2 ) ( F2 F2 ) d r2 0
. . . . . . . . . . . . . ....
mN ( v N dv N ) ( FN FN ) d rN 0
mi v i 2
mi ( v i dv i ) d (
) dK
2
i 1
i 1
N
( Fi Fi )d r2 dA dU
N
Первое слагаемое:
Второе слагаемое:
N
i 1
d (K U ) 0

7. Закон сохранения энергии

d (K U ) 0
E
K U E
-Энергия, константа не зависящая от времени,
Закон сохранения энергии
В системе материальных точек, где действуют только
консервативные силы, сумма потенциальной и
кинетической энергий - постоянная величина.
•С точки зрения теоретической физики ЗСЭ связан с симметрией
пространства относительно сдвигов во времени.
•ЗСЭ может выполняться и для неконсервативных систем (например,
систем с магнитным полем)
•Для квантовых флуктуаций ЗСЭ может нарушаться на сверхмалые
времена

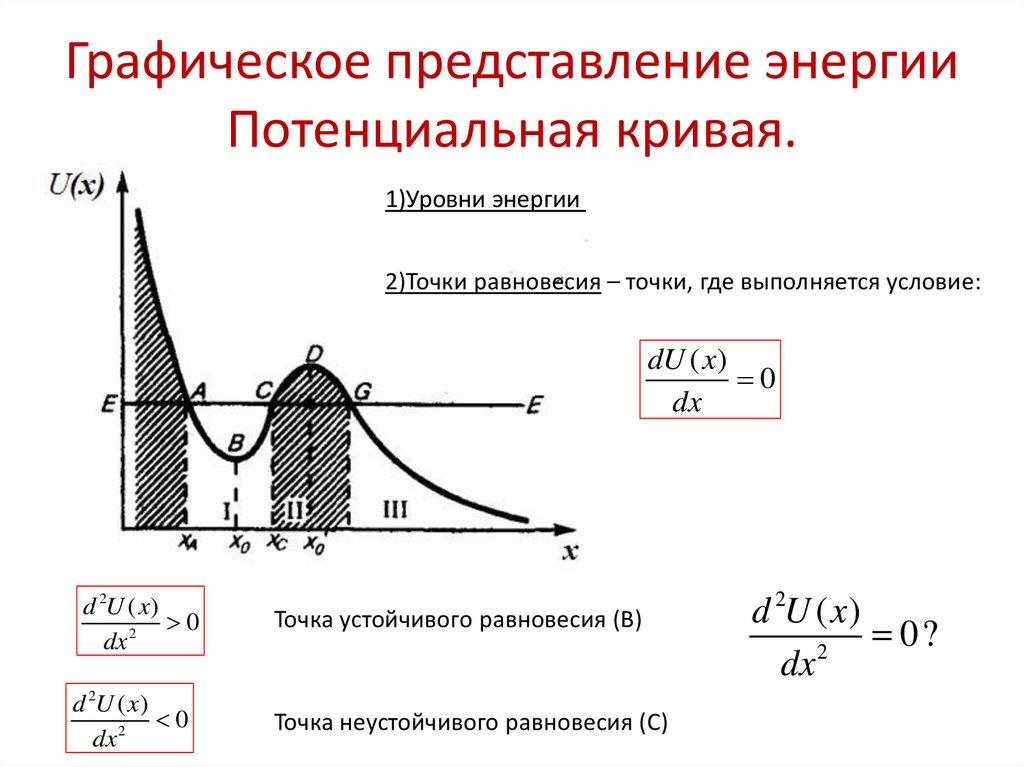
8. Графическое представление энергии Потенциальная кривая.

1)Уровни энергии
2)Точки равновесия – точки, где выполняется условие:
dU ( x)
0
dx
d 2U ( x)
0
2
dx
d 2U ( x)
0
2
dx
Точка устойчивого равновесия (B)
Точка неустойчивого равновесия (C)
d 2U ( x)
0?
2
dx

9. Решение одномерных задач

K U E
Закон сохранения энергии
2
2
m dx
E U ( x)
2 dt
m dx
U ( x) E
2 dt
dx
2( E U ( x)) / m
dt
dx
dt
2( E U ( x)) / m
Переменные разделяются
x
x0
dx
t t0
2( E U ( x)) / m
Одномерная задача с ЗСЭ всегда сводится к интегралу!

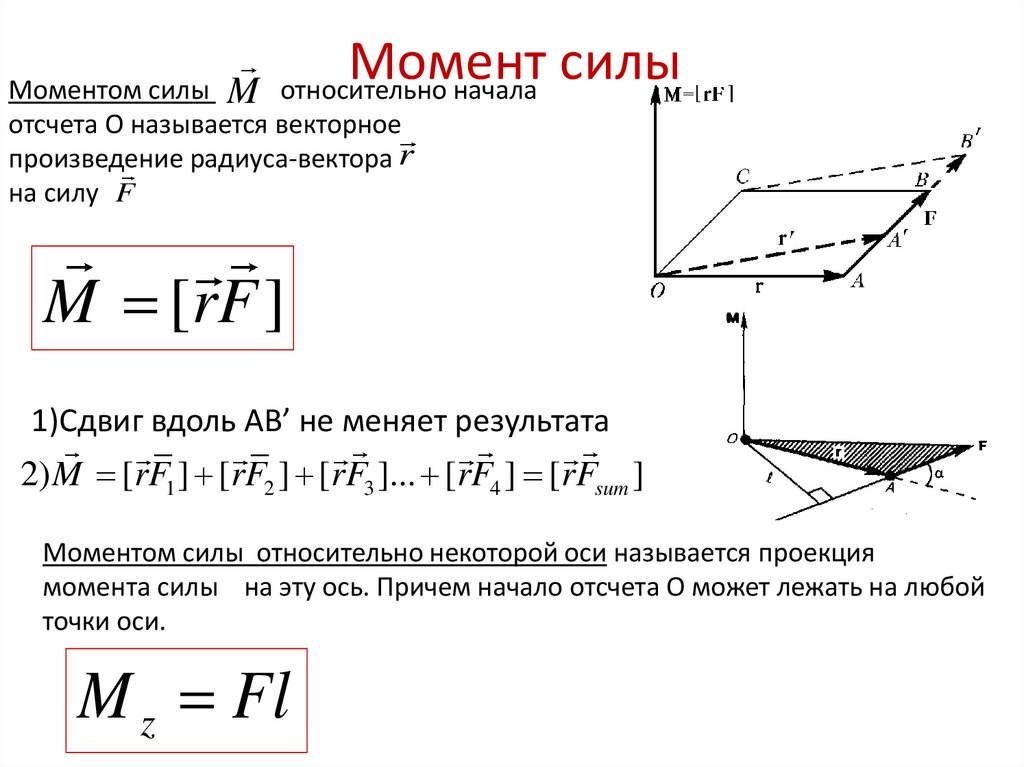
10. Момент силы

Моментом силы M относительно начала
отсчета О называется векторное
произведение радиуса-вектора r
на силу F
M [rF ]
1)Сдвиг вдоль АB’ не меняет результата
2) M [rF1 ] [rF2 ] [rF3 ]... [rF4 ] [rFsum ]
Моментом силы относительно некоторой оси называется проекция
момента силы на эту ось. Причем начало отсчета О может лежать на любой
точки оси.
M z Fl

11. Момент импульса материальной точки

p mv
- импульс материальной точки
Моментом импульса материальной точки относительно
начала отсчета О называется векторное произведение
радиуса-вектора r
на импульс p
.
r
L [rp ]
Моментом импульса материальной точки относительно
некоторой оси, называется проекция момента импульса на
эту ось. Причем начало отсчета О может лежать на любой
точки оси.
Lz pl

12. Динамика вращения материальной точки

L [rp ]
- момент импульса материальной точки
d
d
dr
dv
dp
L [rp ] [ mv ] m[r ] [r ]
dt
dt
dt
dt
dt
Из второго начала Ньютона:
dL
[rF ]
dt
dL
M
dt
•Следствия:
Центральные силы (действующие из начала координат) не изменяют момент
импульса.
•Орбита планеты лежит в одной плоскости
•Второй закон Кеплера (заметаемые планетой площади равны за равные
промежутки времени)

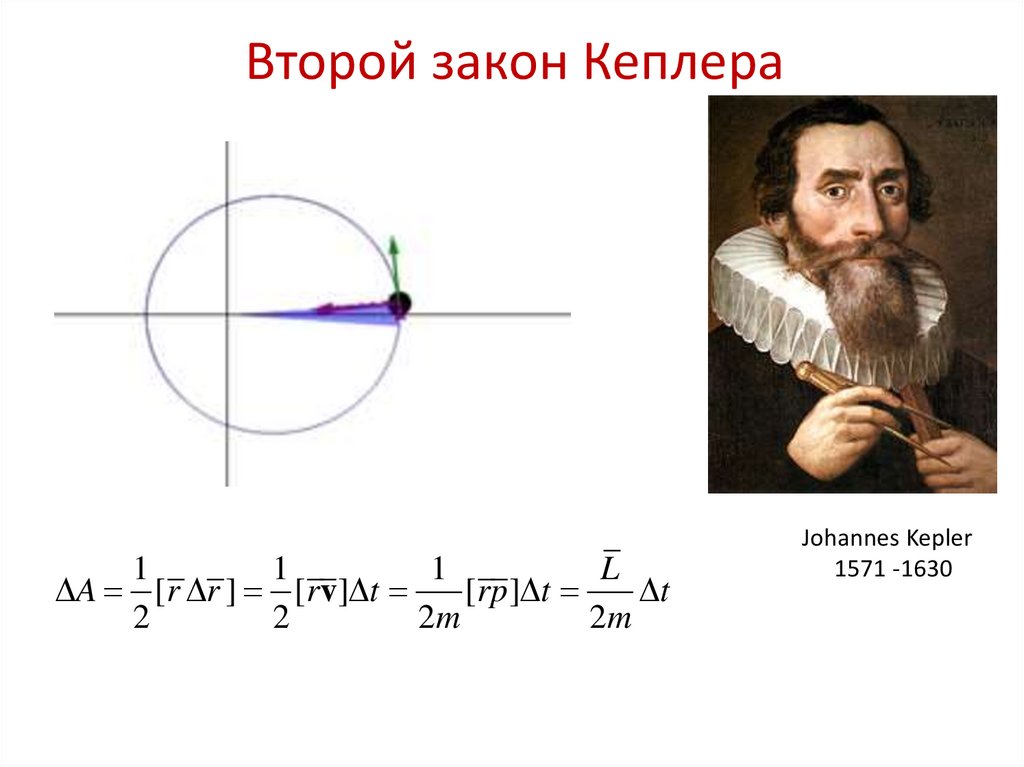
13. Второй закон Кеплера

1
1
1
L
A [r r ] [rv] t
[rp ] t
t
2
2
2m
2m
Johannes Kepler
1571 -1630

14. Момент импульса для системы из двух материальных точек

Второй закон Ньютона для 2 материальных точек:
r1
r2
dv 1
F12 f1
dt
dv 2
m2
F21 f 2
dt
.
m1
F12 -сила действующая на 1-частицу со стороны 2-частицы.
F21 -сила действующая на 2-частицу со стороны 1-частицы.
f1 и f 2
- внешние сила действующие на 1 и 2 частицу.
Третий закон Ньютона:
F12 F21

15. Момент импульса для системы из двух материальных точек

[r1
dv1
dv
dr
d
] [r1 1 ] [ 1 v1 ] ([ r1 v1 ])
dt
dt
dt
dt
dv 2
dv 2
dr2
d
[r2
] [r2
] [
v 2 ] ([ r2 v 2 ])
dt
dt
dt
dt
d
d
d
([r1m1 v1 ] [r2 m2 v 2 ]) ([r1 p1 ] [r2 p2 ]) L sum
dt
dt
dt
(NB ) Суммарный момент сил равен суммарному моменту внешних сил:
M sum [r1 f1 ] [r2 f 2 ]
[(r1 r2 ) F12 ]) 0.
так как [(r1 F12 ]) [(r2 F21 ]) 0.
(!!!) Из третьего закон Ньютона силы, действующие между
двумя материальными точками лежат на прямой,
которая их соединяет
d
L sum M sum
dt

16. Динамика вращательного движения системы материальных точек

Второй закон Ньютона для N материальных точек:
r1
r2
...
rN
dv1
F12 F13 ... F1 N f1
dt
dv 2
m2
F21 F23 ... F2 N f 2
dt
. . . . . . . . . . . . . ....
dv N
mN
FN 1 FN 2 .. FN ( N 1) f N
dt
m1
Fij -сила действующая на i-частицу со стороны j-частицы.
fi - внешняя сила действующая на i – частицу.
Третий закон Ньютона:
F12 F21
F23 F32 Fij Fji

17. Динамика вращения системы материальных точек

Динамика вращения системы N
материальных точек
dv1
F12 F13 ... F1 N f1
dt
dv 2
m2
F21 F23 ... F2 N f 2
dt
. . . . . . . . . . . . . ....
dv N
mN
FN 1 FN 2 .. FN ( N 1) f N
dt
m1
N
L sum [ rp
i i ]
i 1
Fij Fji
[( ri rj ) Fij ] 0
N
M sum [ ri fi ]
i 1
Закон динамики вращения
системы материальных точек :
dL sum
M sum
dt

18. Динамика вращения системы N материальных точек

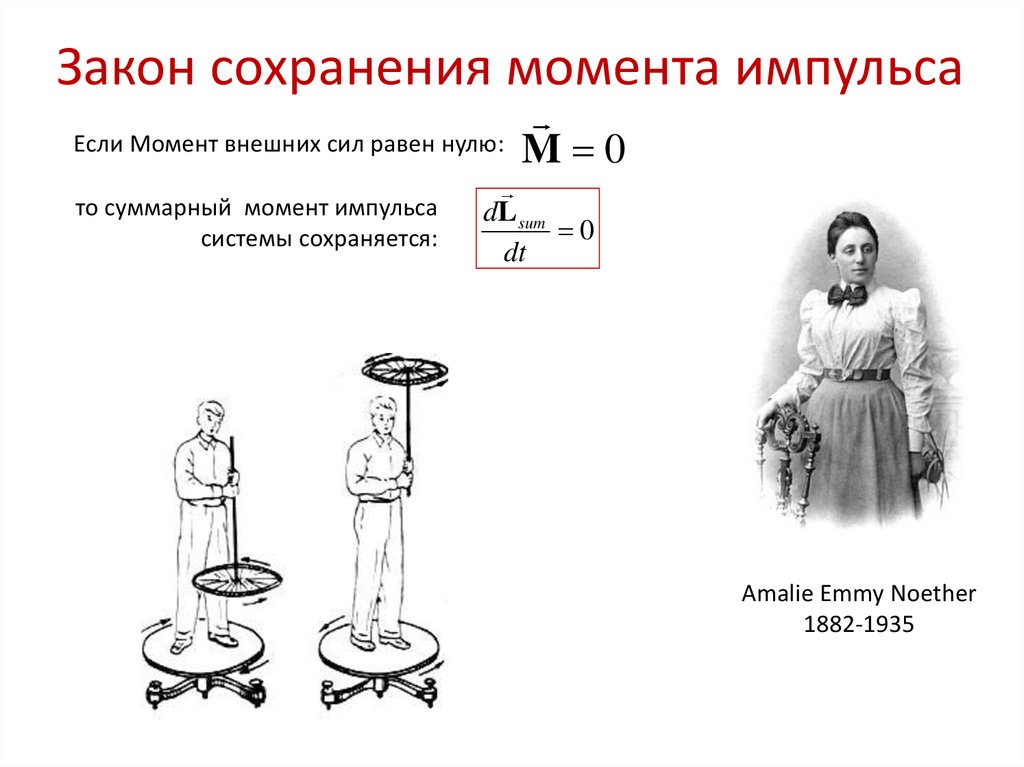
Закон сохранения момента импульса
Если Момент внешних сил равен нулю:
то суммарный момент импульса
системы сохраняется:
M 0
dL sum
0
dt
Amalie Emmy Noether
1882-1935

19. Закон сохранения момента импульса

Момент импульса твердого тела
Момент импульса твердого тела есть сумма всех моментов
импульсов материальных точек, из которых оно состоит.
N
L [ri mi vi ]
i 1
Если твердое тело вращается вокруг некоторой
неподвижной оси z тогда проекция момента импульса на
эту ось будет:
N
L [r i mi vi ]
i 1
L mi ( (r i r i ) ri ( r i ))
L mi [r i [ r i ]]
i 1
i 1
N
N
Lz mi r i z J z z
2
i 1
N
N
J z mi r i 2
i 1
Момент инерции тела
относительно оси z

20. Момент импульса твердого тела

Уравнение динамики вращательного
движения твердого тела вокруг
неподвижной оси
L J
d ( J )
J M sum
dt
L
- проекция момента импульса на ось вращения
J
- момент инерции относительно оси вращения
- угловая скорость вращения
M sum
N
J mi r i 2
i 1
- угловое ускорения
- Суммарный момент внешних сил относительно оси
вращения

21. Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси

Момент инерции
N
J mi ri
2
Моментом инерции системы или тела,
состоящего из материальных точек
i 1
J r dm
2
V
Моментом инерции системы или
непрерывного тела

22. Момент инерции

Моменты инерции некоторых тел
Шар
J
2 2
mr
5
Однородная
пластинка
J
1
m( a 2 b 2 )
12
Тонкостенная
сфера
J
2 2
mr
3
Сплошной
цилиндр
J
1 2
mr
2
Однородный
стержень
J
1 2
ml
12
Толстостенный
цилиндр
J
1
m(r12 r22 )
2
Диск
J
1 2
mr
2
Диск
J
1 2
mr
4
Тонкостенный
цилиндр
Произвольное
тело
J mr 2
I mi ri 2

23.

Работа силы поворота твердого тела
вокруг неподвижной оси
dA FdS sin( )
dS rd
Работа силы F
Сдвиг
dA Fr sin( )d
M rF sin( ) Fl
l – плечо
dA Md

24. Работа силы поворота твердого тела вокруг неподвижной оси

N
J M mi ri 2
Теорема Штейнера
Момент инерции относительно оси, проходящей через
центр масс.
i 1
N
J mi (ri )
ri ri a
Момент инерции относительно оси параллельной первой
, но отстающей на расстояние а
2
i 1
N
N
N
N
i 1
i 1
i 1
i 1
J mi (ri a ) 2 mi ri 2 mi a 2 2 mi (ri a )
N
N
N
i 1
i 1
i 1
J mi ri 2 a 2 mi 2a ( mi ri ) J M Ma 2
Момент инерции тела относительно оси,
образованной параллельным переносом
оси, проходящей через центр масс,
увеличивается Ma2 , где M – масса тела, а
– расстояние между осями
J J M Ma 2

25. Теорема Штейнера

Кинетическая энергия вращения
твердого тела
mi vi 2
K
2
i 1
N
система из N материальных точек
v1 / r1 v2 / r2 v3 / r3 . .. vN / rN
mi 2 ri 2 2
K
2
2
i 1
N
K
J
N
2J
i 1
2
2
m
r
ii
Из теоремы Кенинга:
J mi ri 2
i 1
2
2
N
J
2
MvM
K
2
2
2

26. Кинетическая энергия вращения твердого тела

Сравнение вращательного и
поступательного движения

27. Сравнение вращательного и поступательного движения

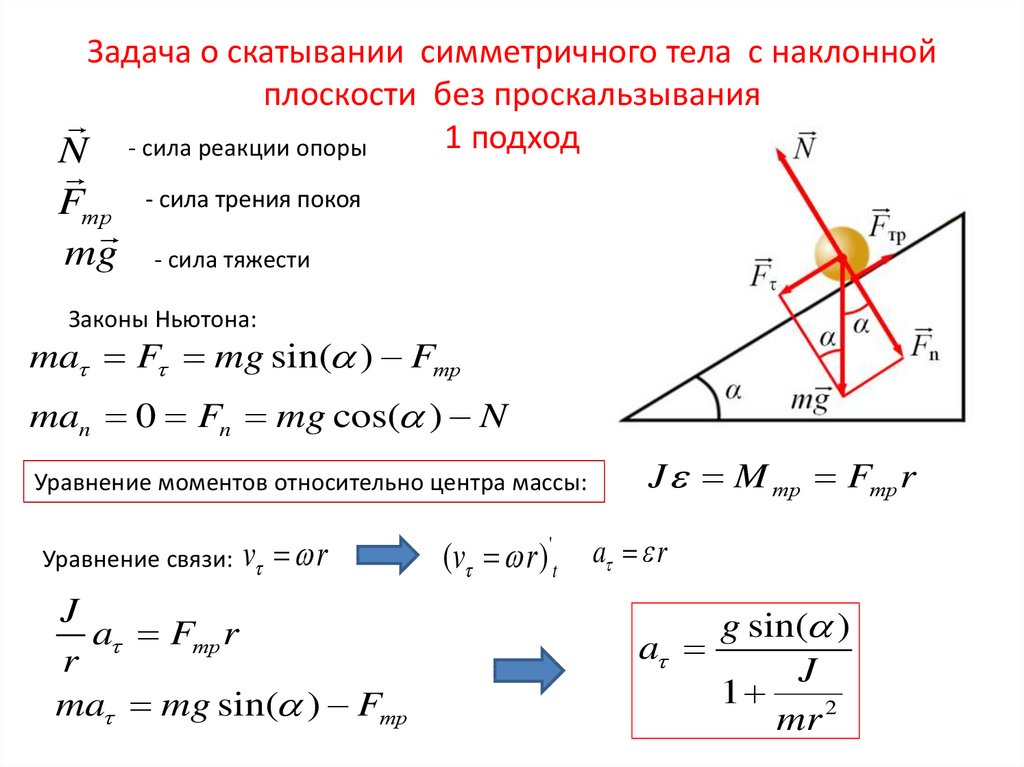
Задача о скатывании симметричного тела с наклонной
плоскости без проскальзывания
1 подход
N - сила реакции опоры
Fтр
mg
- сила трения покоя
- сила тяжести
Законы Ньютона:
ma F mg sin( ) Fтр
man 0 Fn mg cos( ) N
Уравнение моментов относительно центра массы:
Уравнение связи: v
r
J
a Fтр r
r
ma mg sin( ) Fтр
J M тр Fтр r
(v r )'t a r
g sin( )
a
J
1
mr 2

28. Задача о скатывании симметричного тела с наклонной плоскости без проскальзывания 1 подход

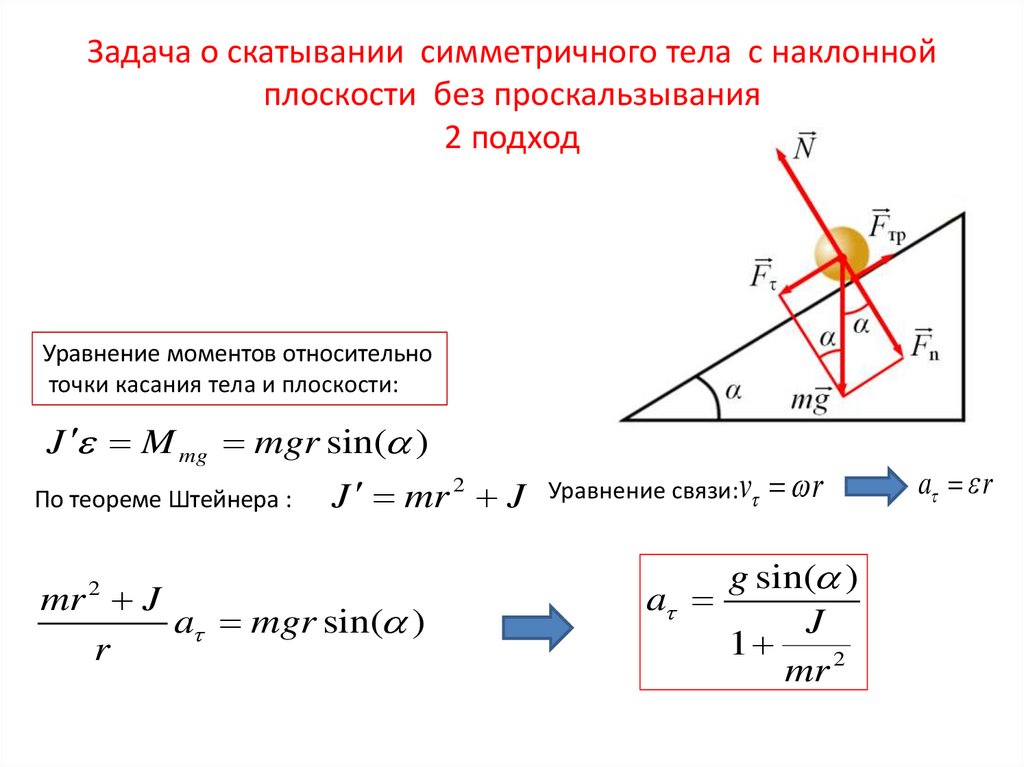
Задача о скатывании симметричного тела с наклонной
плоскости без проскальзывания
2 подход
Уравнение моментов относительно
точки касания тела и плоскости:
J M mg mgr sin( )
По теореме Штейнера :
J mr 2 J
mr J
a mgr sin( )
r
2
Уравнение связи:v
r
g sin( )
a
J
1
mr 2
a r

29. Задача о скатывании симметричного тела с наклонной плоскости без проскальзывания 2 подход

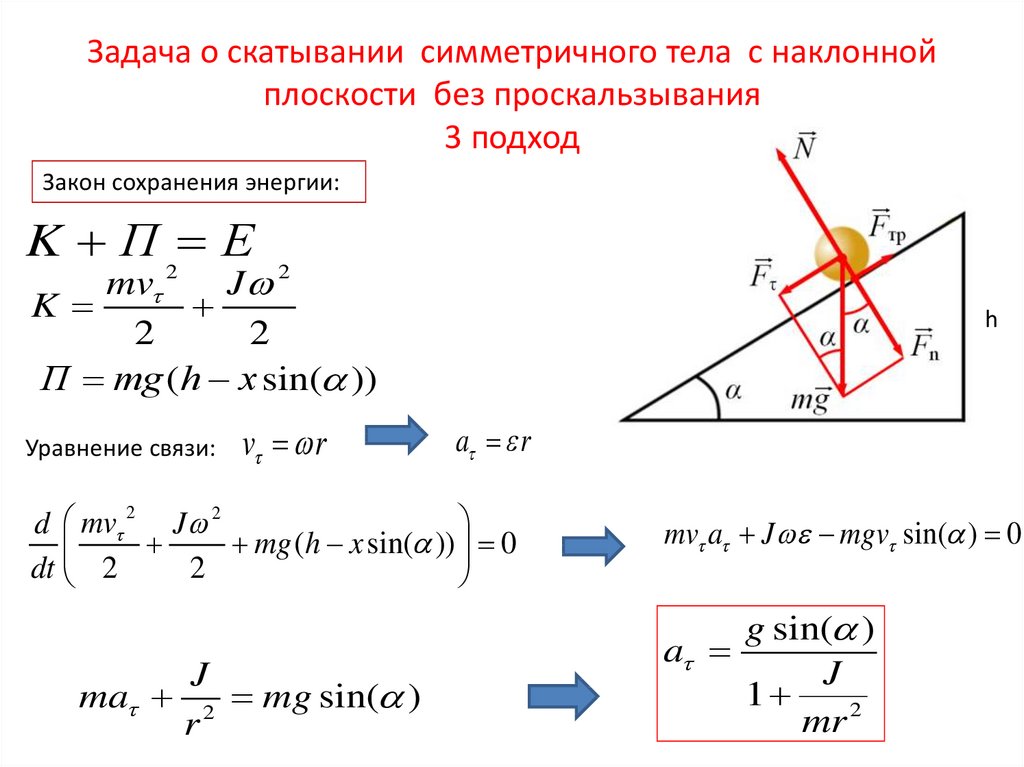
Задача о скатывании симметричного тела с наклонной
плоскости без проскальзывания
3 подход
Закон сохранения энергии:
K П 2 E
mv
J 2
K
2
2
П mg (h x sin( ))
Уравнение связи:
v r
h
a r
d mv 2 J 2
mg (h x sin( )) 0
dt 2
2
J
ma 2 mg sin( )
r
mv a J mgv sin( ) 0
g sin( )
a
J
1
mr 2