Лекция № 4. Динамика вращательного движения

1. Лекция № 4. (27.02.15) ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

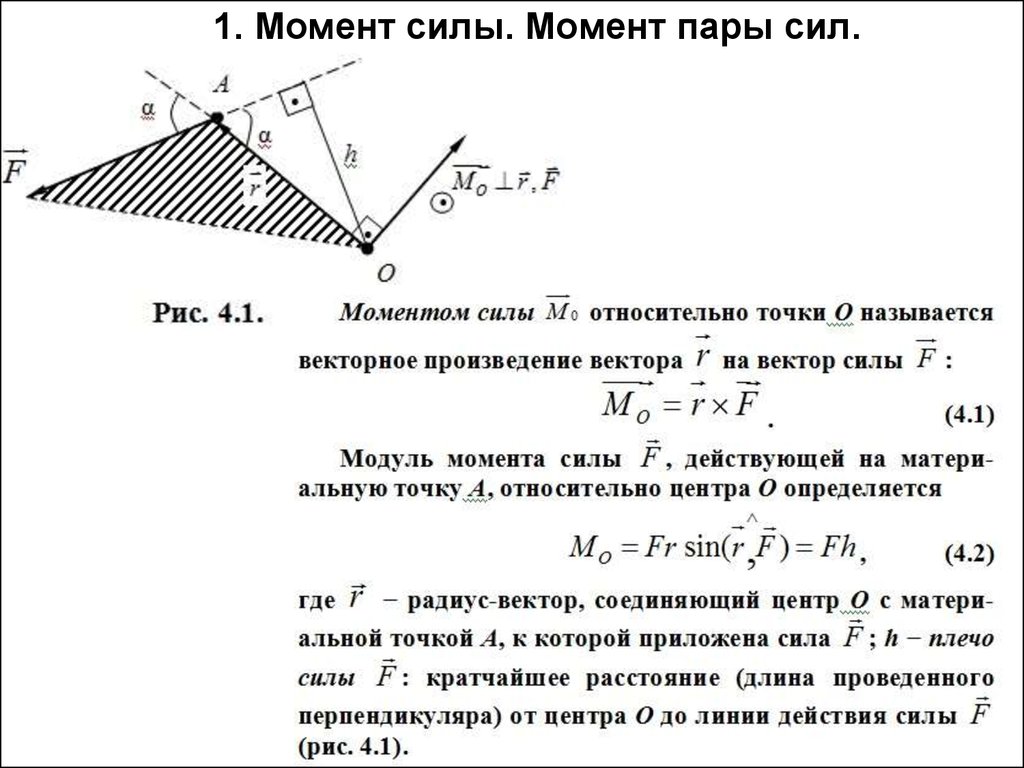
1. Момент силы. Момент пары сил.
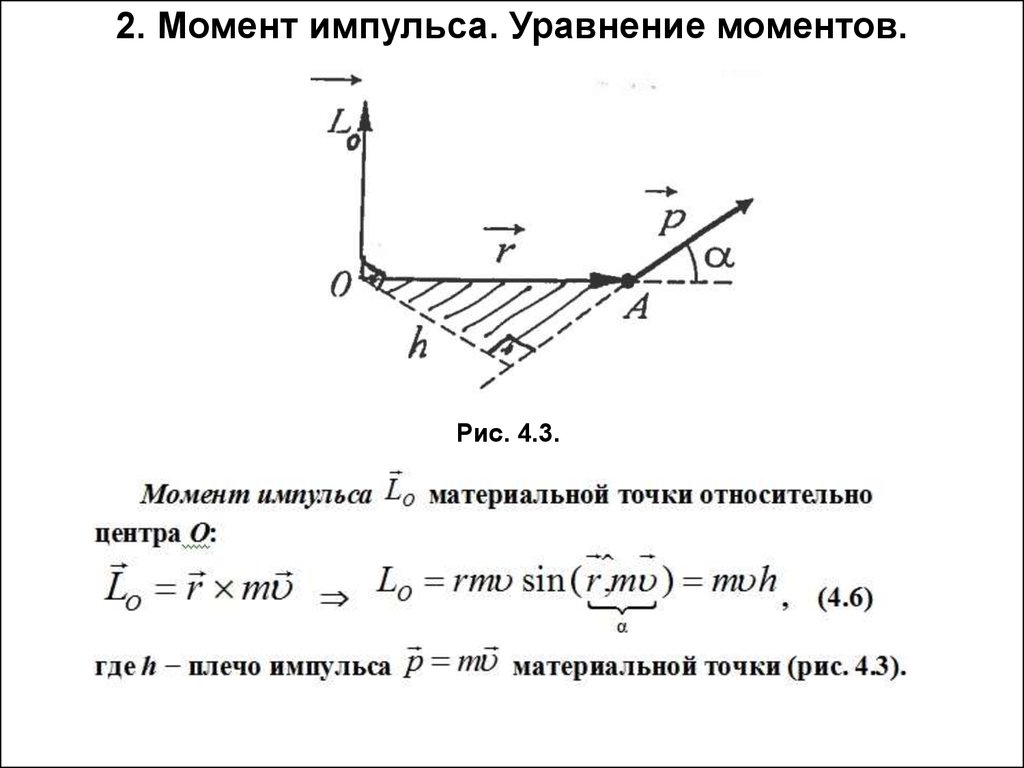
2. Момент импульса. Уравнение моментов.
3. Проекция вектора момента импульса на ось Z.
4. Динамика вращения твердого тела вокруг
неподвижной оси.
5. Момент инерции. Момент импульса
вращающегося тела.
6. Основное уравнение динамики вращательного
движения.
7. Закон сохранения момента импульса.
8. Закон сохранения проекции вектора момента
импульса.
9. Моменты инерции однородных тел.
10. Теорема Штейнера.

2. 1. Момент силы. Момент пары сил.

3. 1. Момент силы. Момент пары сил.

4. 2. Момент импульса. Уравнение моментов.

Рис. 4.3.

5. 2. Момент импульса. Уравнение моментов.

Продифференцируем по времени выражение для
момента импульса L r m
Имеем:
dp
dL
dr
[ , p] [r , ]
dt
dt
dt
(4.7)
1-ое слагаемое равно 0, так как 2 вектора умножаются
векторно сами на себя, ибо
dr/dt = v, p = mv, т.е. [v, mv] =v mv sin0º = 0.
Тогда
dL dp
[r , ] [r , F ] M
dt
dt
(4.8)

6.

Полученное выражение
носит название уравнение моментов,
т.к. связывает между собой
момент силы и момент импульса!
dL/dt = M
d LO i N
M Oi ,
dt
i 1
(4.9)
(4.9’)
т.е. скорость изменения момента импульса системы материальных
точек относительно точки О равна векторной сумме моментов всех
внешних сил, действующих на систему, относительно этой же точки
О.

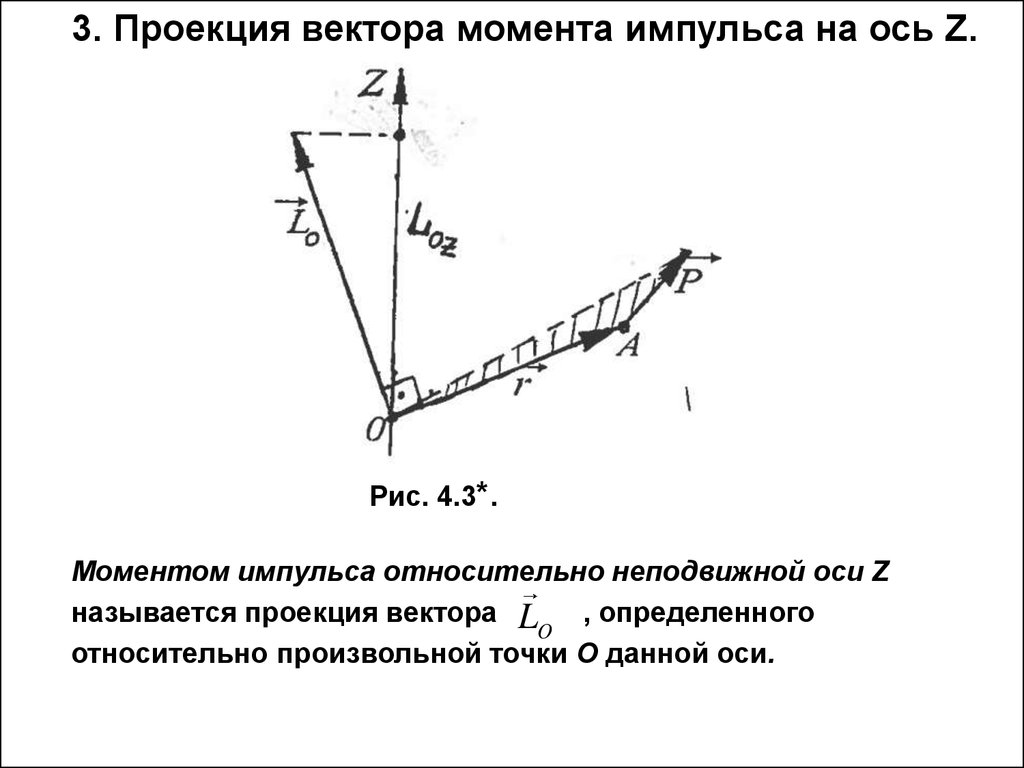
7. 3. Проекция вектора момента импульса на ось Z.

Рис. 4.3*.
Моментом импульса относительно неподвижной оси Z
называется проекция вектора L
, определенного
O
относительно произвольной точки О данной оси.

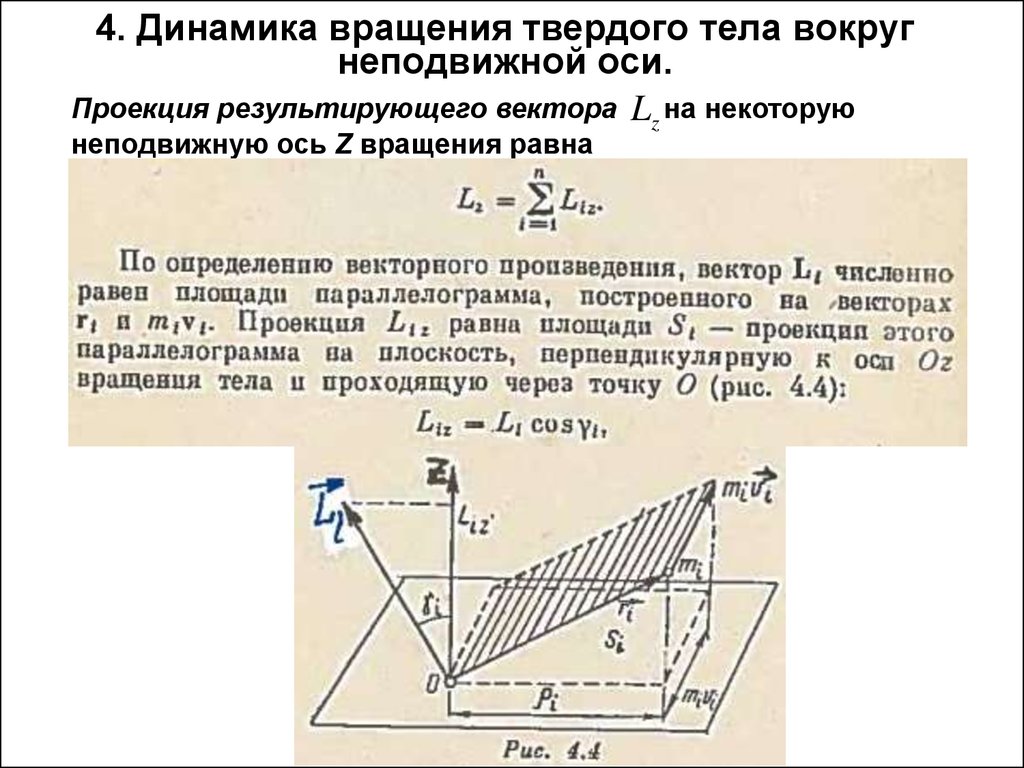
8. 4. Динамика вращения твердого тела вокруг неподвижной оси.

9. 4. Динамика вращения твердого тела вокруг неподвижной оси.

Проекция результирующего вектора Lz на некоторую
неподвижную ось Z вращения равна

10. 4. Динамика вращения твердого тела вокруг неподвижной оси.

11. 5. Момент инерции. Момент импульса вращающегося тела.

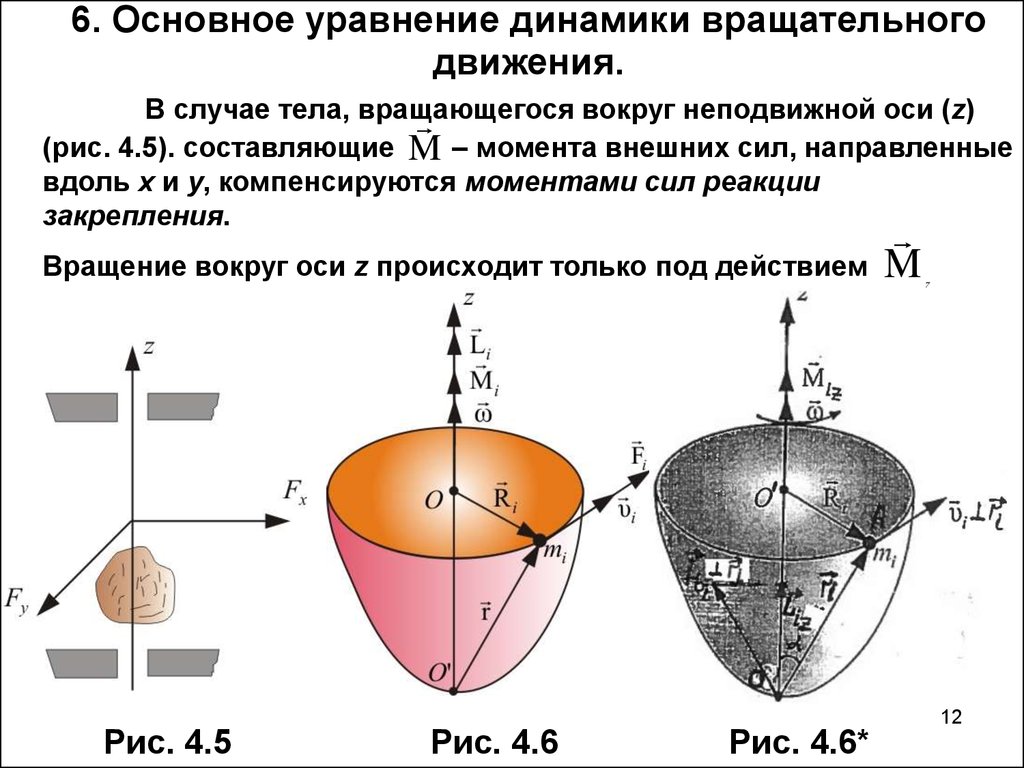
12. 6. Основное уравнение динамики вращательного движения.

В случае тела, вращающегося
вокруг неподвижной оси (z)
(рис. 4.5). составляющие M – момента внешних сил, направленные
вдоль x и y, компенсируются моментами сил реакции
закрепления.
Вращение вокруг оси z происходит только под действием
Рис. 4.5
Рис. 4.6
Рис. 4.6*
M
z
12

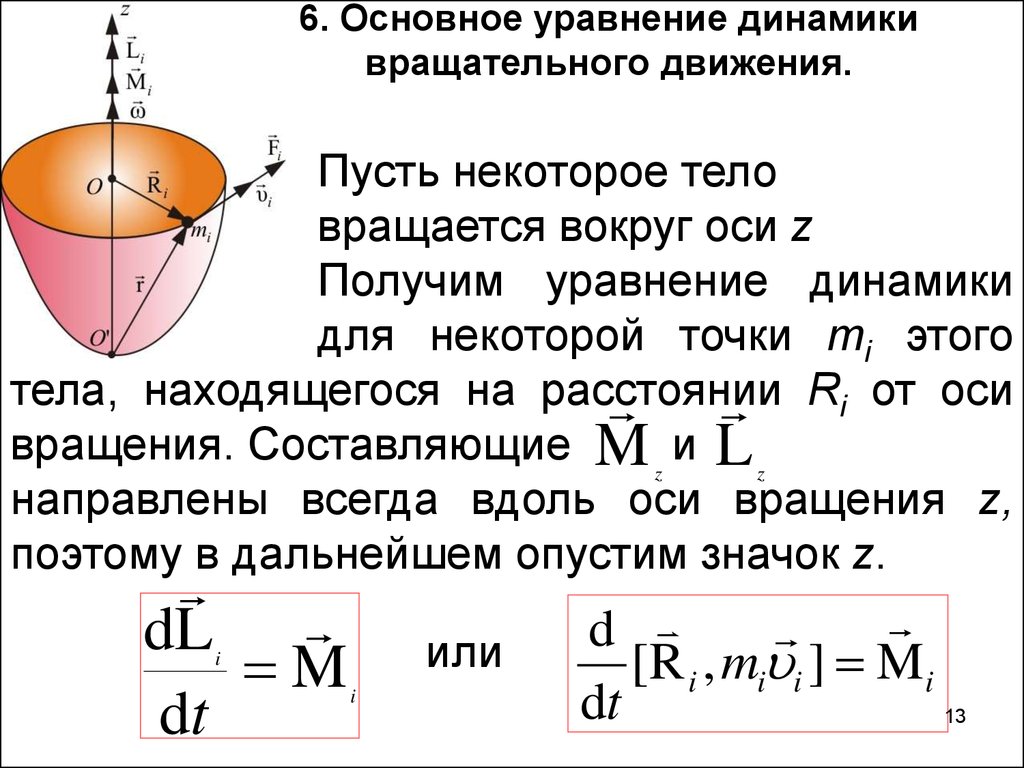
13. 6. Основное уравнение динамики вращательного движения.

Пусть некоторое тело
вращается вокруг оси z
Получим уравнение динамики
для некоторой точки mi этого
тела, находящегося на расстоянии
Ri от оси
вращения. Составляющие M z и L z
направлены всегда вдоль оси вращения z,
поэтому в дальнейшем опустим значок z.
dL
M
dt
или
i
i
d
[R i , mi i ] Mi
dt
13

14.

Так как i у всех точек
разная, используем ω
вектор угловой скорости,
причем модуль ω .
R
d
m R ω M
dt
2
Тогда
i
i
i
Так как тело абсолютно твердое, то в
процессе вращения mi и Ri останутся
неизменными. Тогда:
dω
mR
M.
dt
2
i
i
i
14

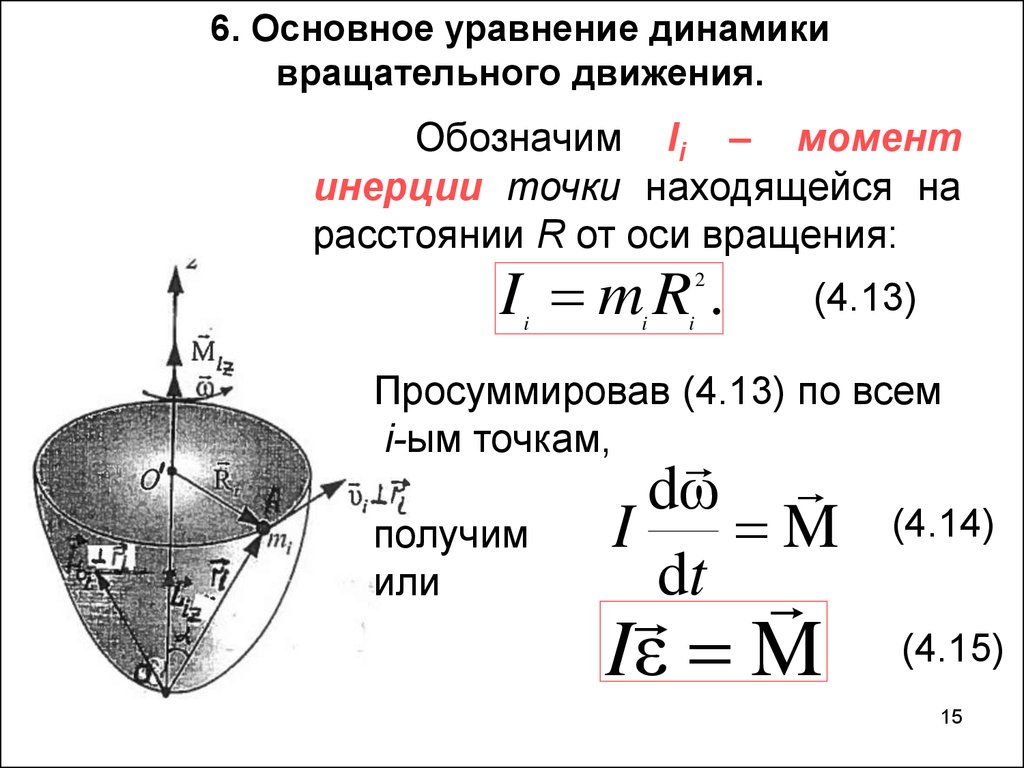
15.

6. Основное уравнение динамики
вращательного движения.
Обозначим Ii – момент
инерции точки находящейся на
расстоянии R от оси вращения:
I mR .
2
i
i
i
(4.13)
Просуммировав (4.13) по всем
i-ым точкам,
получим
или
dω
I
M
dt
Iε M
(4.14)
(4.15)
15

16.

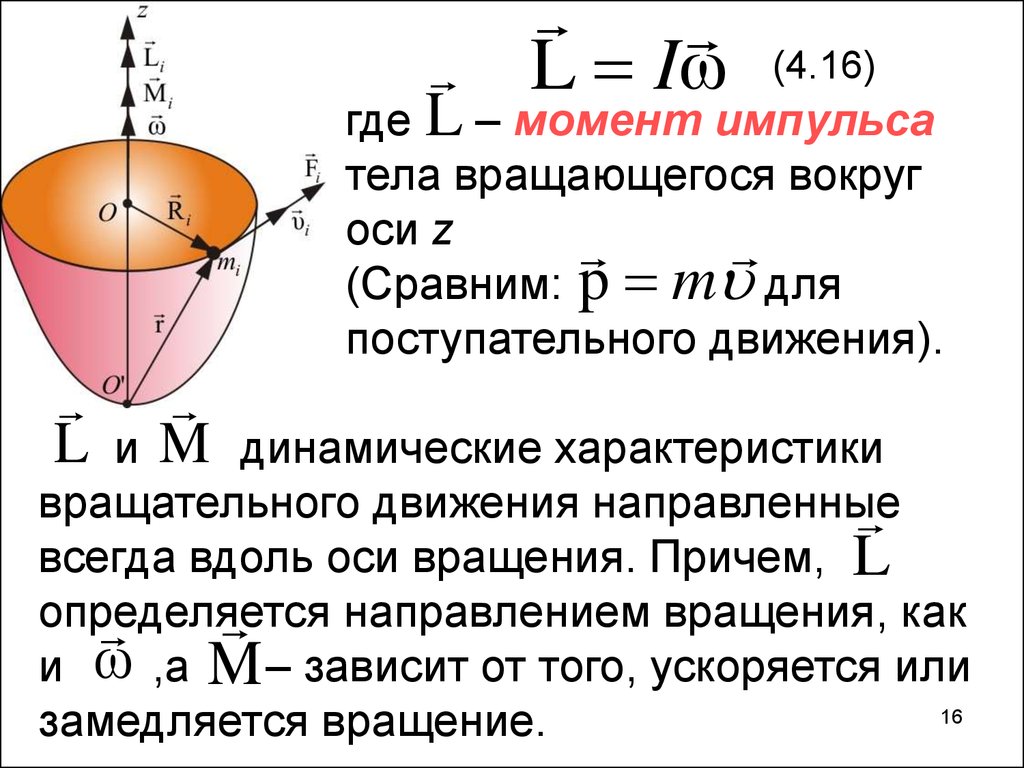
L Iω
(4.16)
где L – момент импульса
тела вращающегося вокруг
оси z
(Сравним: p m для
поступательного движения).
L
M
и
динамические характеристики
вращательного движения направленные
всегда вдоль оси вращения. Причем, L
определяется
направлением вращения, как
и ω ,а M – зависит от того, ускоряется или
16
замедляется вращение.

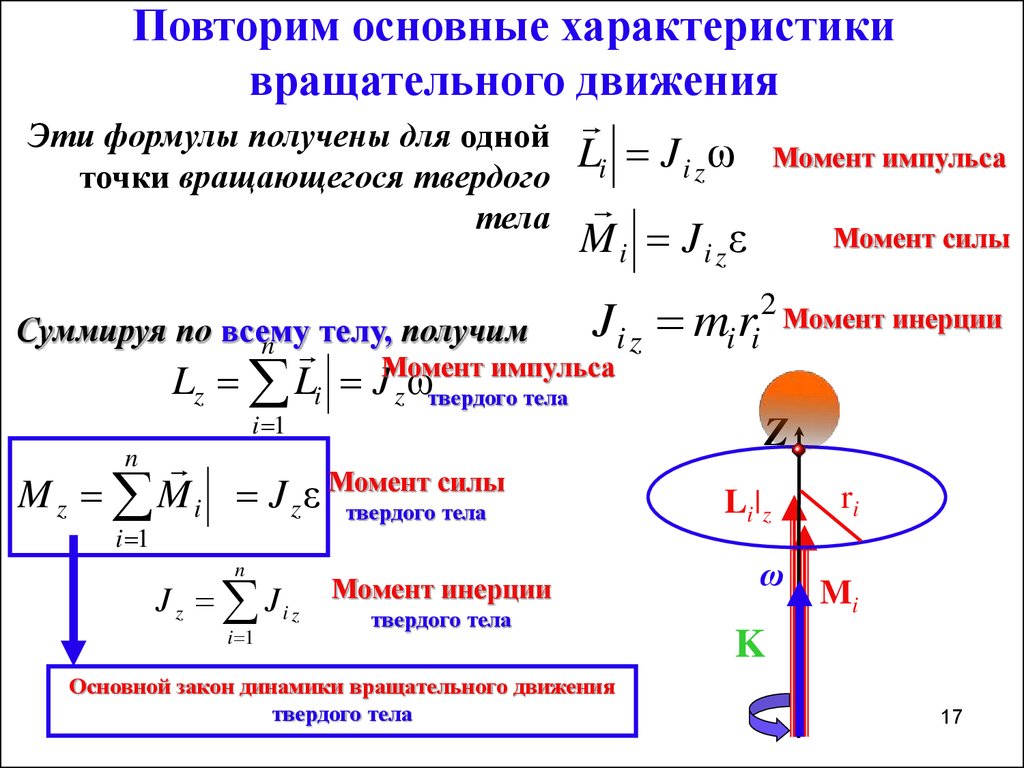
17. Повторим основные характеристики вращательного движения

Эти формулы получены для одной
точки вращающегося твердого
тела
Суммируя по всему
телу, получим
n
Li J i z ω
M i Ji zε
J i z mi ri
импульса
Lz Li JМомент
ω
z твердого тела
i 1
силы
M z M i J z ε Момент
твердого тела
n
i 1
n
J z Ji z
i 1
Момент инерции
твердого тела
Основной закон динамики вращательного движения
твердого тела
Момент импульса
Момент силы
2 Момент инерции
Z
Li|z
ω
ri
Mi
K
17

18. 7. Закон сохранения момента импульса.

Для замкнутой системы тел момент
внешних сил M всегда равен нулю, так как
внешние силы вообще не действуют на замкнутую
систему:
dL
M 0
dt
L const,
(4.17)
Закон сохранения момента импульса можно применять и
к незамкнутой системе тел, если …………
18

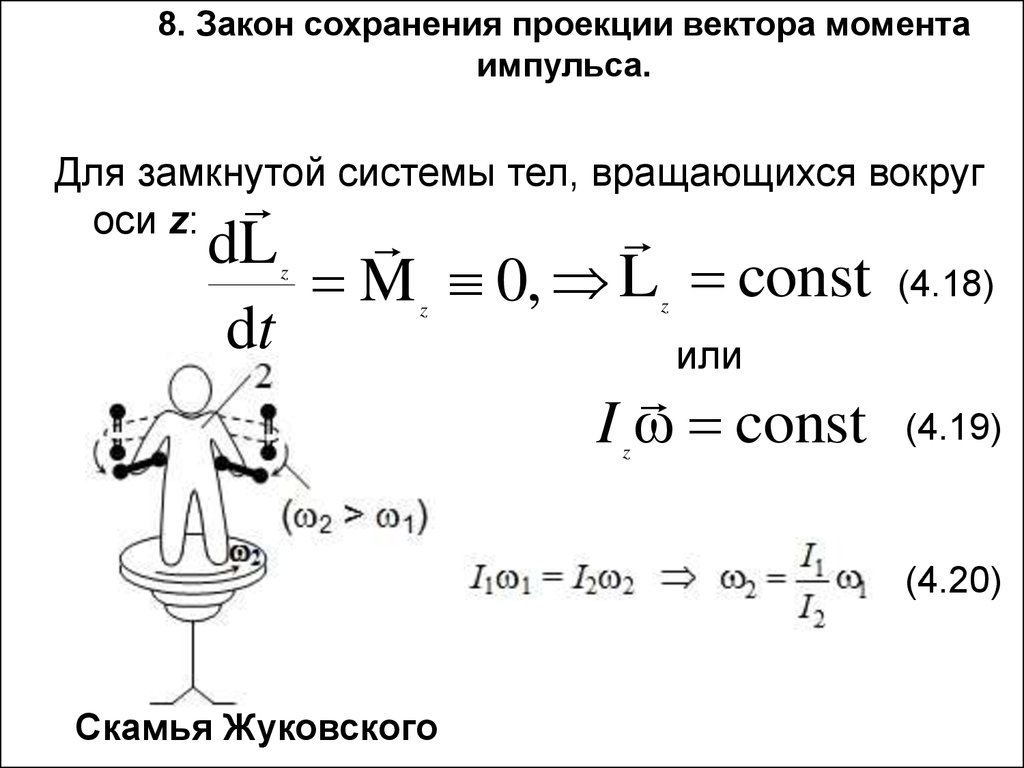
19. 8. Закон сохранения проекции вектора момента импульса.

Для замкнутой системы тел, вращающихся вокруг
оси z:
dL
M 0, L const
dt
или
I ω const
z
z
z
z
(4.18)
(4.19)
(4.20)
Скамья Жуковского

20.

9. Моменты инерции однородных тел.
(шара, сферы, диска, обруча и стержня)
Шар
Стержень
Диск
1
I 2 5 m R ; I c 1 2 m R ; I ml
12
2
2
c
c
Сфера
I 2 3 m R ;
2
c
Обруч
I m R
c
2
20
2

21.

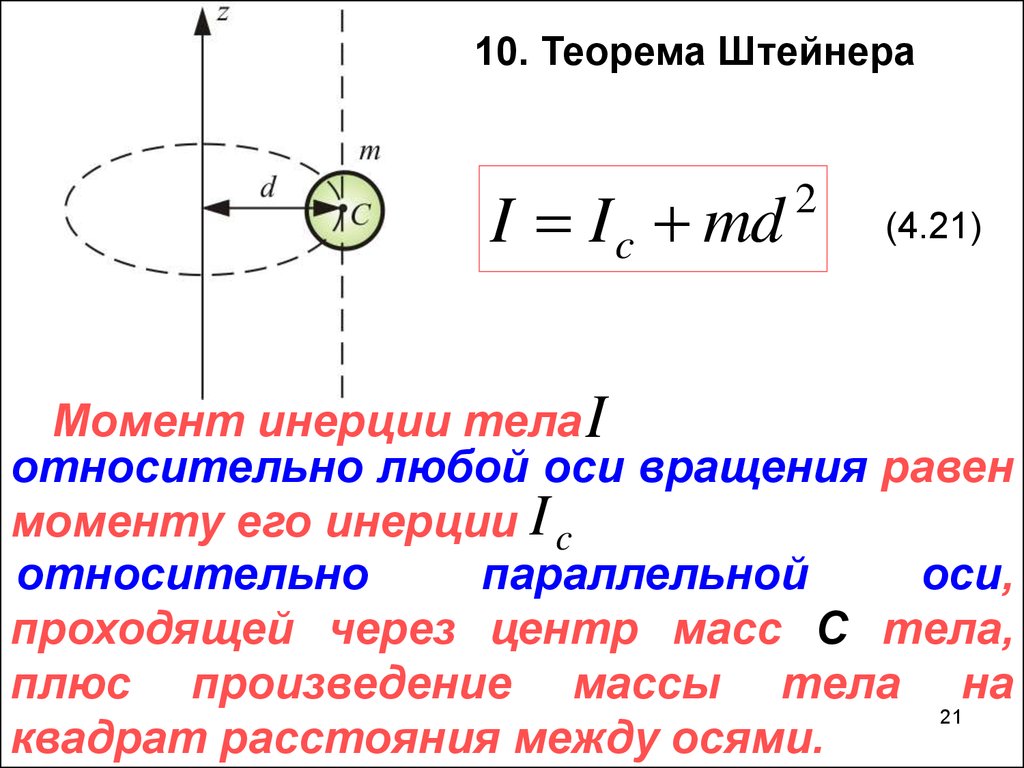
10. Теорема Штейнера
I I c md
2
(4.21)
Момент инерции тела I
относительно любой оси вращения равен
моменту его инерции I c
относительно
параллельной
оси,
проходящей через центр масс С тела,
плюс произведение массы тела на
21
квадрат расстояния между осями.

22.

10. Теорема Штейнера
Пример: стержень массой m,
длиной l, вращается вокруг оси,
проходящей через конец
стержня (рис).
1 2
I c ml
12
2
1
1 2 1 2
l
I z I c m ml ml ml .
4
3
2 12
22

23.

dp
F
dt
ma F
p m
m const
A FS
N Fv
m
mgh const
2
2
dL
M
dt
Iε M
L Iω
Iω const
A Mф
N Mw
Iω
mgh const
2
2
23

24.

Если изучение физики порождает:
беспокойство, замешательство, страх,
уныние или негодование, то это
привычное с детства отношение к
возникшим трудностям !!!
Надо незамедлительно заменить на
прямо противоположное и проблема
начнет решаться быстро и легко…
24