Similar presentations:
Динамика вращательного движения
1. Динамика вращательного движения
2.
Лекцию читаетКандидат физико-математических
наук, доцент
Кузьмин Юрий Ильич
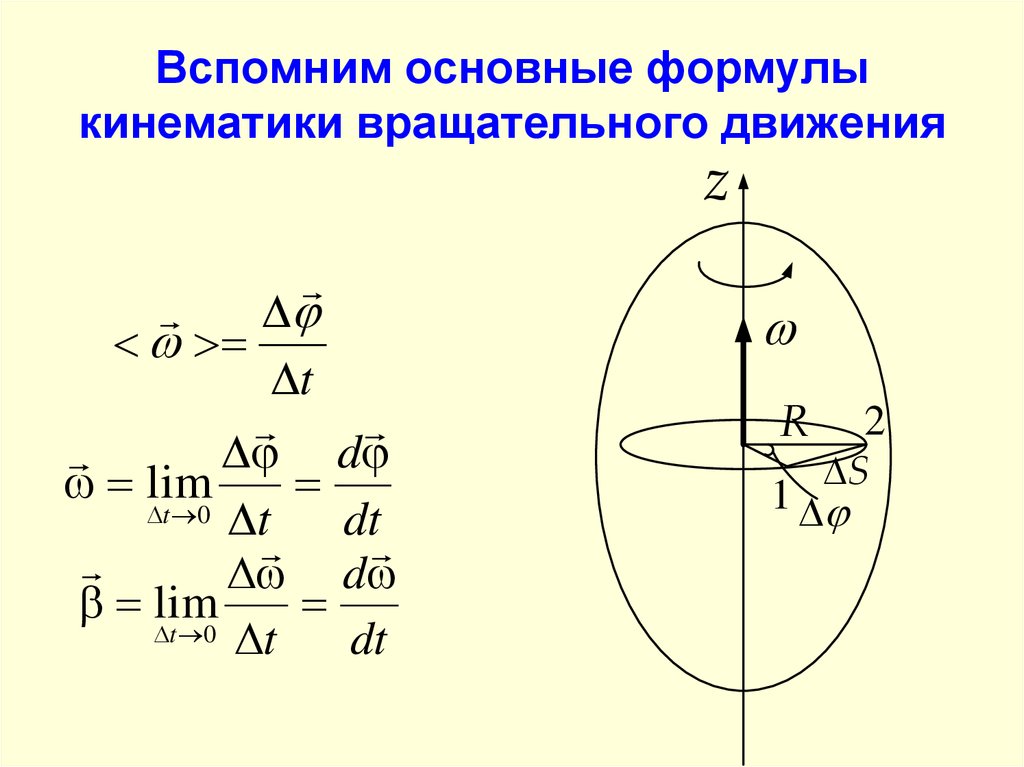
3. Вспомним основные формулы кинематики вращательного движения
zt
d
lim
t 0 t
dt
d
lim
t 0 t
dt
R
2
S
1
4.
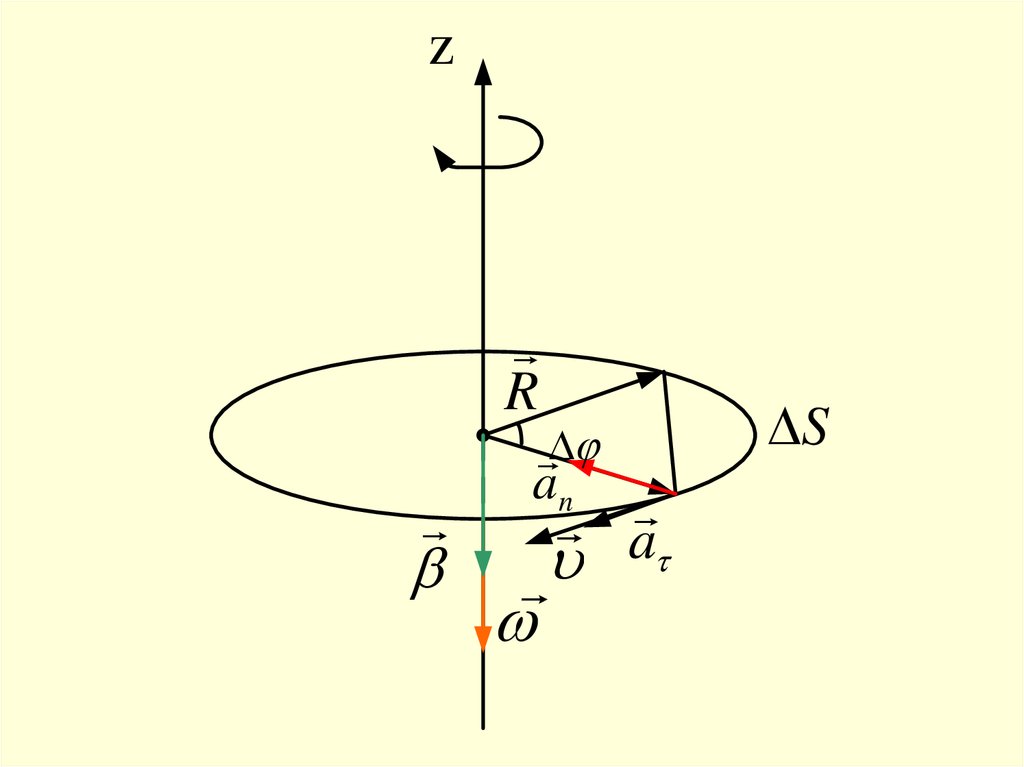
zR
an
a
S
5.
1. МОМЕНТЫ СИЛЫ• Определим момент силы относительно
• центра вращения О
(1)
М [r , F ]
• M – векторная величина, определяемая
• векторным произведением радиус
• вектора
на силу F
r
6.
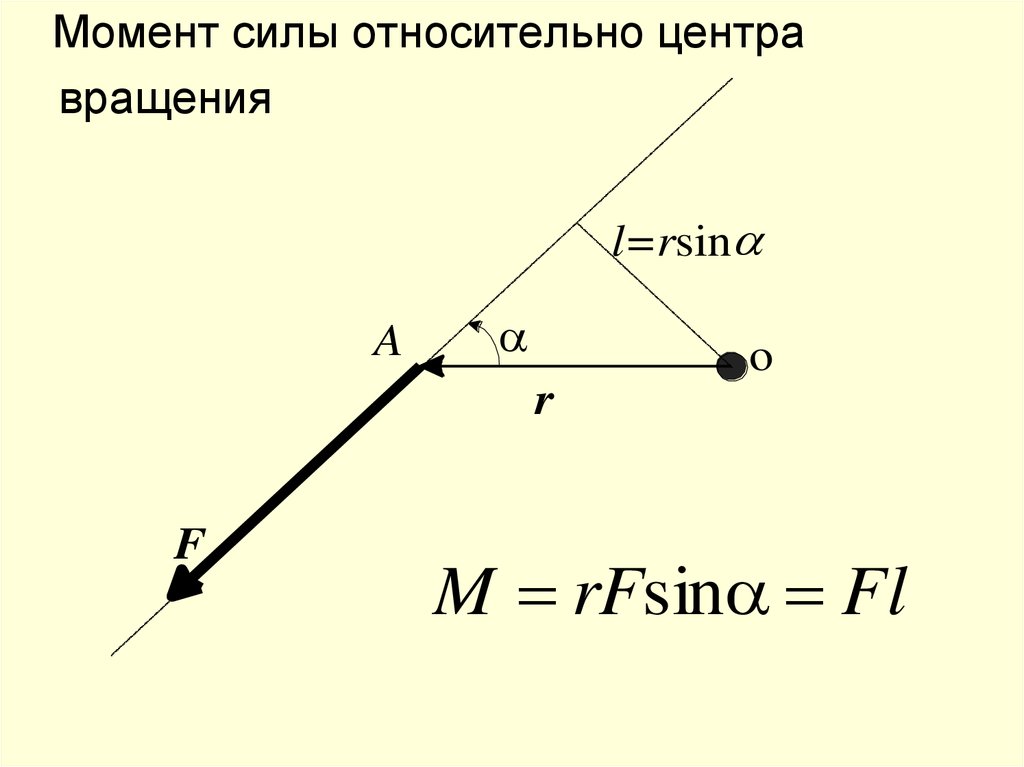
Момент силы относительно центравращения
l=rsin
A
o
r
F
M rFsin Fl
7.
Вначале определим момент силыотносительно точки (О): это векторная
величина определяемая векторным
произведением радиус-вектора на силу.
М [r , F ]
(1)
Направление определяется правилом
буравчика. Момент силы относительно оси
вращения - это скалярная величина,
равная проекции на эту ось вектора
М Z [ r , F ]Z
(2)
8.
zМ [r , F ]
М Z [ r , F ]Z
R
r
Rz
М Z R, F Z RZ , F
Z
R, F
Z
F
0
9.
Разложимr
на две составляющие.
r R RZ
(3)
Подставив (3) в выражение (2), получим
МZ
R, F
Z
RZ , F
Z
R, F
Z
т.к. второй член в выражении (4) равен нулю.
(4)
10.
2. МОМЕНТ ИНЕРЦИИ.МОМЕНТ ИМПУЛЬСА.
• Определение момента инерции
элементарного объема относительно
оси вращения:
I i mi R
2
i
(1)
11.
• Так как абсолютно твердое телонедеформируемо, то момент инерции
твердого тела равен сумме моментов
инерции элементарных объемов:
n
I mi R
i 1
2
i
(2)
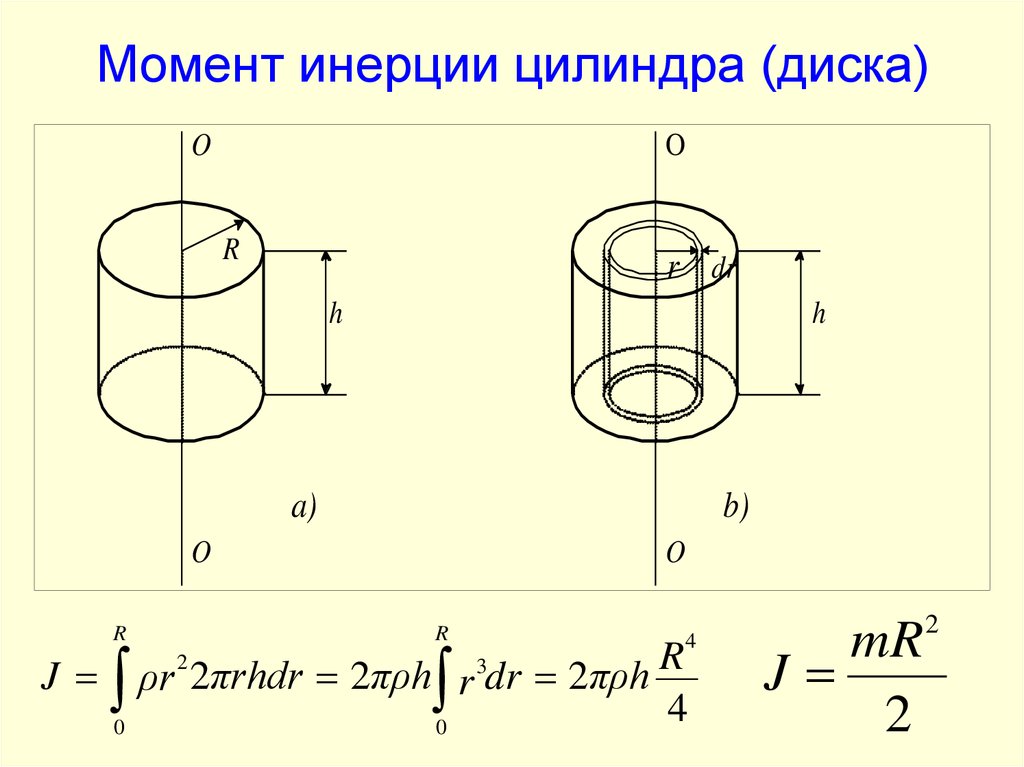
12. Момент инерции цилиндра (диска)
OO
R
r dr
h
h
a)
b)
O
R
J
0
O
R
4
R
ρr 2πrhdr 2πρh r dr 2πρh
4
0
2
3
mR
J
2
2
13.
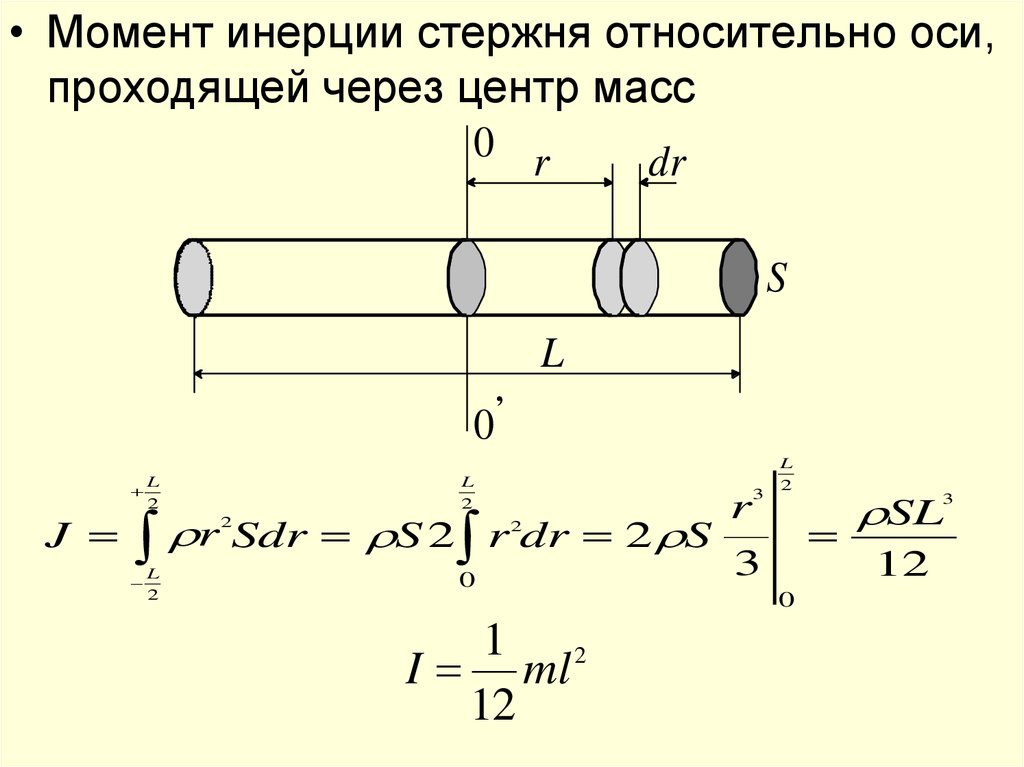
• Момент инерции стержня относительно оси,проходящей через центр масс
0 r
dr
S
L
0
L
2
’
L
2
J r Sdr S 2 r dr 2 S
2
L
2
2
0
r
3
L
2
3
0
1 2
I ml
12
SL
3
12
14. Момент инерции тел относительно неподвижной оси, проходящей через центр симметрии. Тела считаются однородными.
Тело1.Полый тонкостенный
цилиндр радиуса R
Момент инерции I
mR2
2. Сплошной цилиндр или диск
радиуса R
1
mR 2
2
3. Шар радиуса R
2
mR 2
5
4.Прямой тонкий стержень
длиной l. Ось вращения
перпендикулярна стержню и
проходит через его середину
1
ml 2
12
15. Момент импульса твердого тела
• Вначале определяем момент импульсаэлементарного объема относительно оси
вращения:
(3)
L R,р
Zi
i
i Z
• где рi mi vi – импульс элементарного
объема.
16.
zLz
Pi
Ri
mi
r
Rz
0
17.
• Затем, просуммировав по всем элементарнымобъемам, получим выражение для момента
импульса твердого тела:
L I
• где I – момент инерции твердого тела.
18.
• Для кинетической энергии вращательногодвижения твёрдого тела
2
2
2
mvc I c (4)
I ;
Еk
2
Еk
2
2
• где Ic – момент инерции тела относительно
оси вращения, проходящей через центр
масс;
• vс– скорость центра масс тела.
19. Основное уравнение динамики вращательного
• Запишем второй закон Ньютона для каждогоэлементарного объема:
Fi mi a i
(1)
Fi – касательная составляющая силы,
a i Ri – тангенциальное ускорение.
• где
a
• Подставим выражение для
в формулу (1) и
i
умножим обе части полученного выражения на Ri.
Тогда:
Fi Ri mi R I i
2
i
(2)
20.
I i mi R – момент инерции• Где
материальной точки относительно оси вращения,
2
i
M i Fi Ri – момент силы относительно оси
вращения.
• Момент M i можно представить как сумму
моментов всех внутренних и внешних сил,
действующих на точку.
• Просуммировав выражение (2) по всем
элементарным объемам получим основное
уравнение динамики вращательного движения:
М I
(3)
21.
• Получимдругую
форму
закона
основного
уравнения
динамики,
используя понятие момента импульса .
• Перепишем выражение (3):
d d ( I ) dL
М I I
dt
dt
dt
dL
M
dt
(4)
22.
• Формулировка: Производная моментаимпульса твердого тела по времени
равна результирующему моменту
всех внешних сил, вызывающих
вращение тела.
dL
• При М 0 ,
,т.е.
0
dt
L I const
(5)
• Это математическая запись закона
сохранения момента импульса.
23.
• Формулировка: Момент импульса системысохраняется, т.е. не изменяется с течением
времени, если сумма моментов сил,
действующих на систему, равна нулю.
• Из закона следует, что так как
сохраняется
постоянным произведение I , то
увеличение момента инерции приводит к
пропорциональному уменьшению частоты
вращения и наоборот.
24. Таблица аналогий величин и законов поступательного и вращательного движения
• ПоступательноеВращательное
• Масса m
Момент инерции I
• Скорость v dr
Угловая скорость d
dt
dv
a
dt
• Ускорение
• Сила F
• Импульс
p mv
dt
Угловое ускорение
d
dt
Момент силы M
Момент импульса
L I
25.
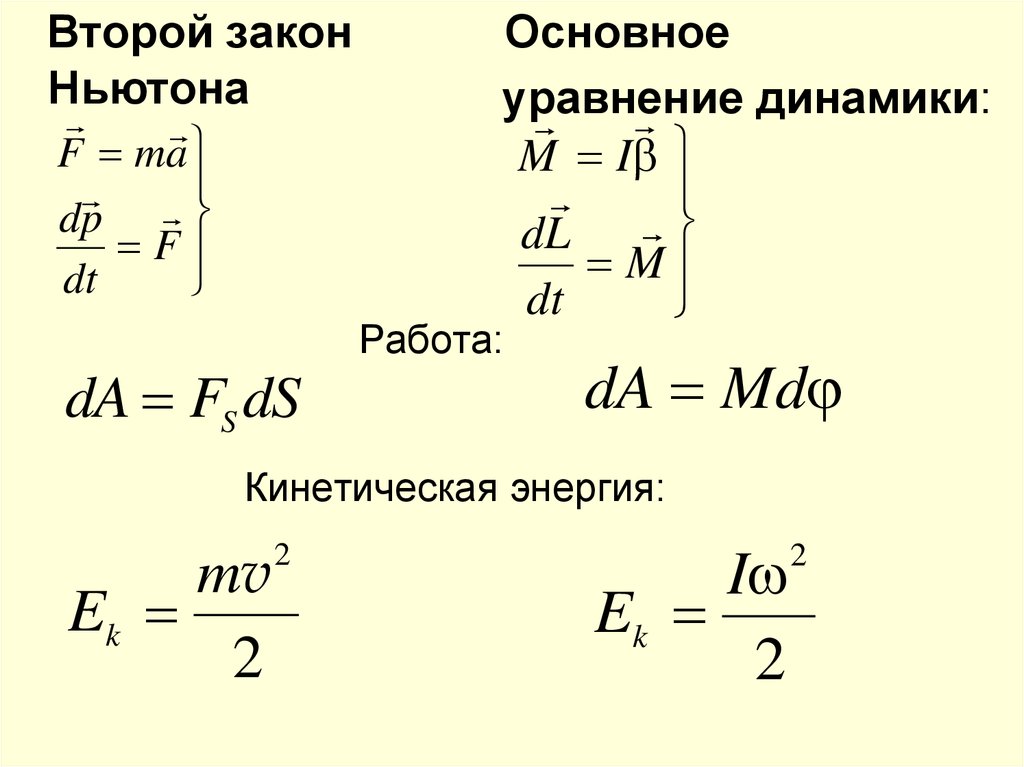
Второй законНьютона
F ma
dp
F
dt
dA FS dS
Основное
уравнение
динамики:
M I
dL
M
dt
Работа:
dA Md
Кинетическая энергия:
mv
Ek
2
2
I
Ek
2
2
26. ЗАДАЧА
• К ободу диска радиусом 0,2 м приложенапостоянная касательная сила 98,1 Н. При
вращении на диск действует момент сил трения,
равный 0,5 Нм. Найти массу диска, если
известно, что диск вращается с постоянным
угловым ускорением 100 рад/с2.
27. Дано:
R 2 10 м1
F 98,1 Н
М тр 0,5 Н м
10 рад/с
2
m=?
2
28. Решение
1.Основное
уравнение
динамики
вращательного движения твердого тела:
(1)
М
I
2
mR – момент инерции диска.
I
2
M F R M тр
(2)
М – результирующий момент всех внешних сил.
После подстановки (2) в (1) с учетом (1)
2
получим
откуда
mR
F R M тр
2
2( FR M тр )
m
2
R
(3)
29. Задача
• На скамье Жуковского стоит человек и держит ввытянутых руках гантели массой 6 кг каждая.
Длина руки человека 60 см. Скамья с человеком
вращается с угловой скоростью 4 рад/с. С какой
угловой скоростью будет вращаться скамья с
человеком, если он опустит руки с гантелями вниз
вдоль оси вращения? Суммарный момент инерции
2
человека и скамьи 5кг м . Гантели считать
материальными точками.
30. Дано:
m1 6 кгR 0,6 м
1 4 рад/с
2
I 0 5 кг м
2
2 = ?
31. Решение
• Закон сохранения момента импульсаL I const
(I 0 2m1 R ) 1 I 0 2
2
• момент инерции гантели
I1 m1R
2
I 0 2m1 R 2
2m1 R
2 6 0 ,36
ω2 ω1
ω1(1
) 4( 1
)
I0
I0
5
4 1 ,87 7 ,48 рад/с.

























 physics
physics








