Пирамида

1.

2. Пирамида

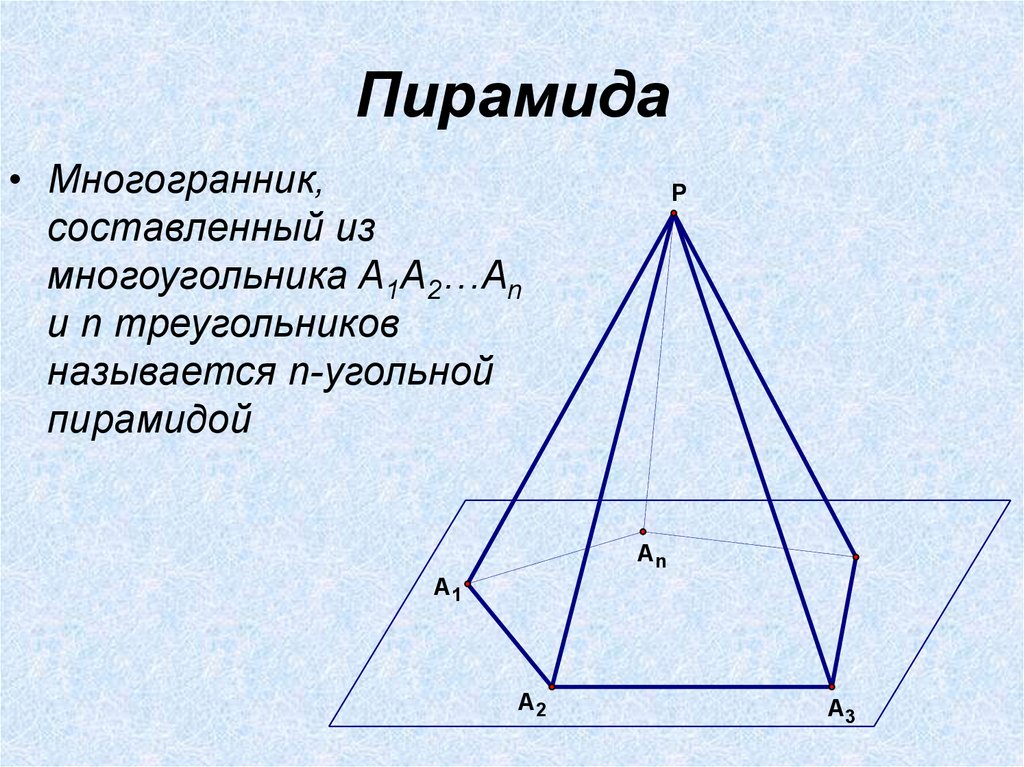
• Многогранник,
составленный из
многоугольника A1A2…An
и n треугольников
называется n-угольной
пирамидой
P
An
A1
A2
A3

3.

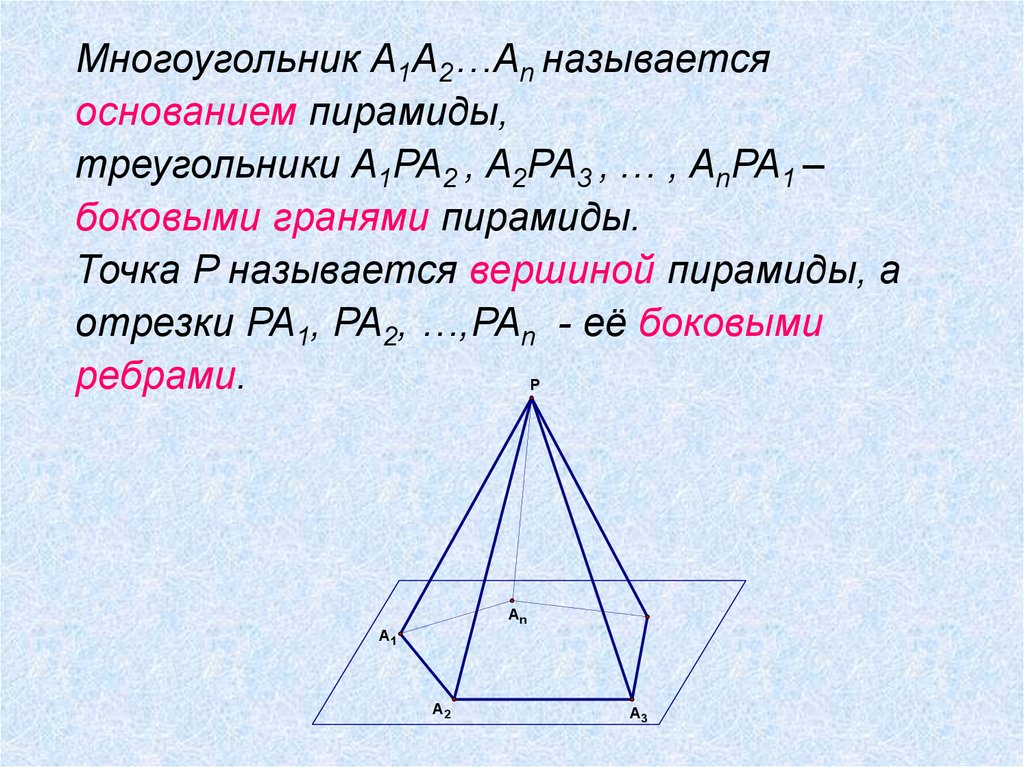
Многоугольник A1A2…An называется
основанием пирамиды,
треугольники A1PA2 , A2PA3 , … , AnPA1 –
боковыми гранями пирамиды.
Точка P называется вершиной пирамиды, а
отрезки PA1, PA2, …,PAn - её боковыми
ребрами.
P
An
A1
A2
A3

4.

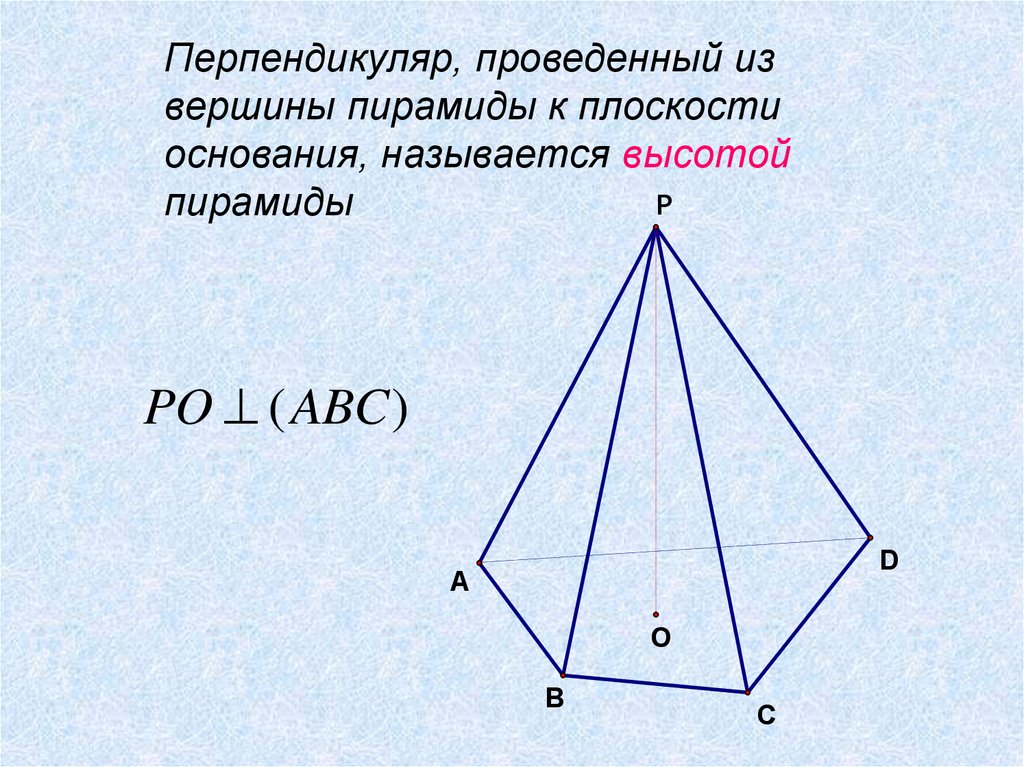
Перпендикуляр, проведенный из
вершины пирамиды к плоскости
основания, называется высотой
P
пирамиды
PO ( ABC )
D
A
O
B
C

5.

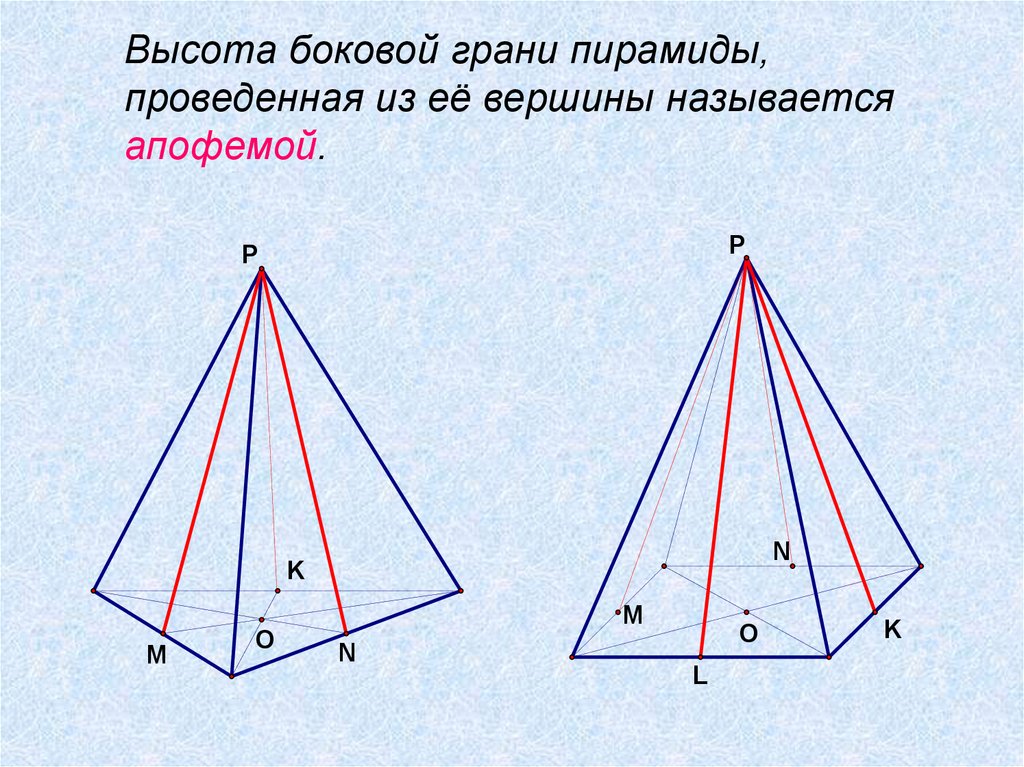
Высота боковой грани пирамиды,
проведенная из её вершины называется
апофемой.
P
P
N
K
M
M
O
N
O
L
K

6.

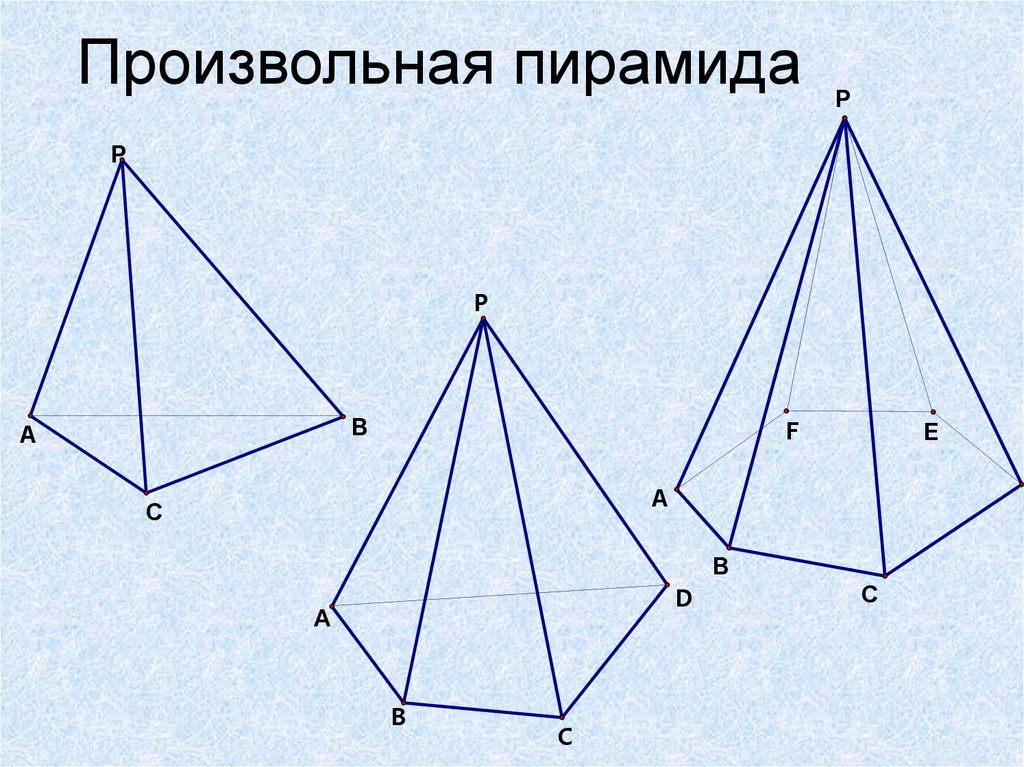
Произвольная пирамида
P
P
P
B
A
F
E
A
C
D
B
D
A
B
C
C

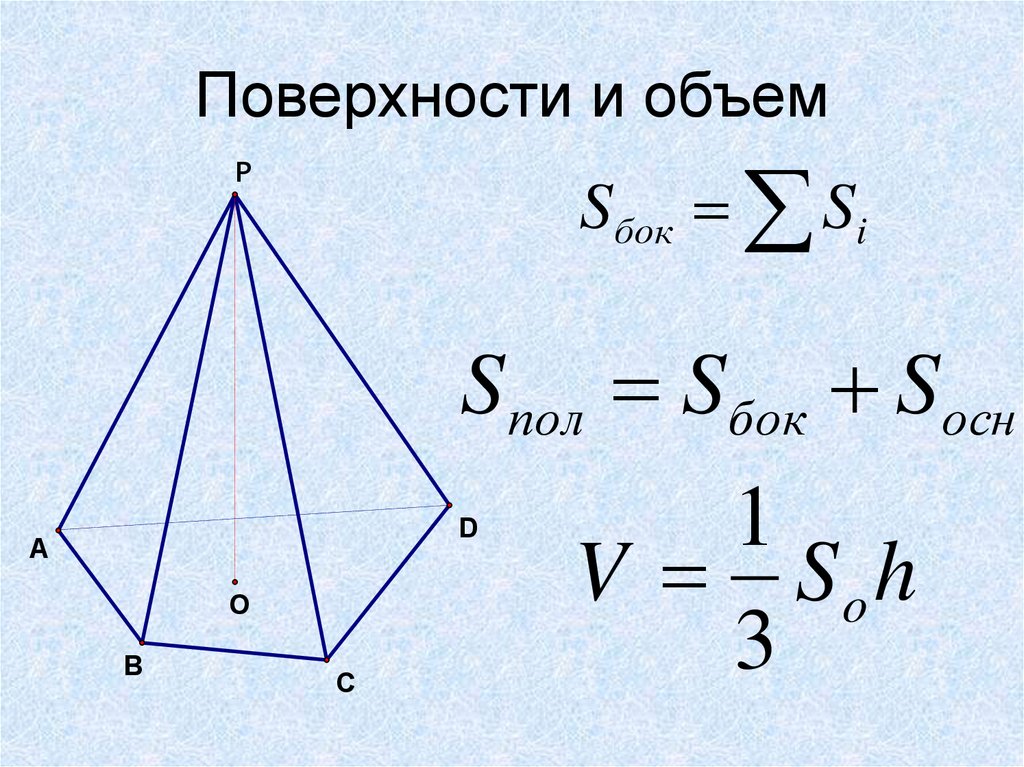
7. Поверхности и объем

Sбок Si
P
S пол Sбок Sосн
D
A
O
B
C
1
V So h
3

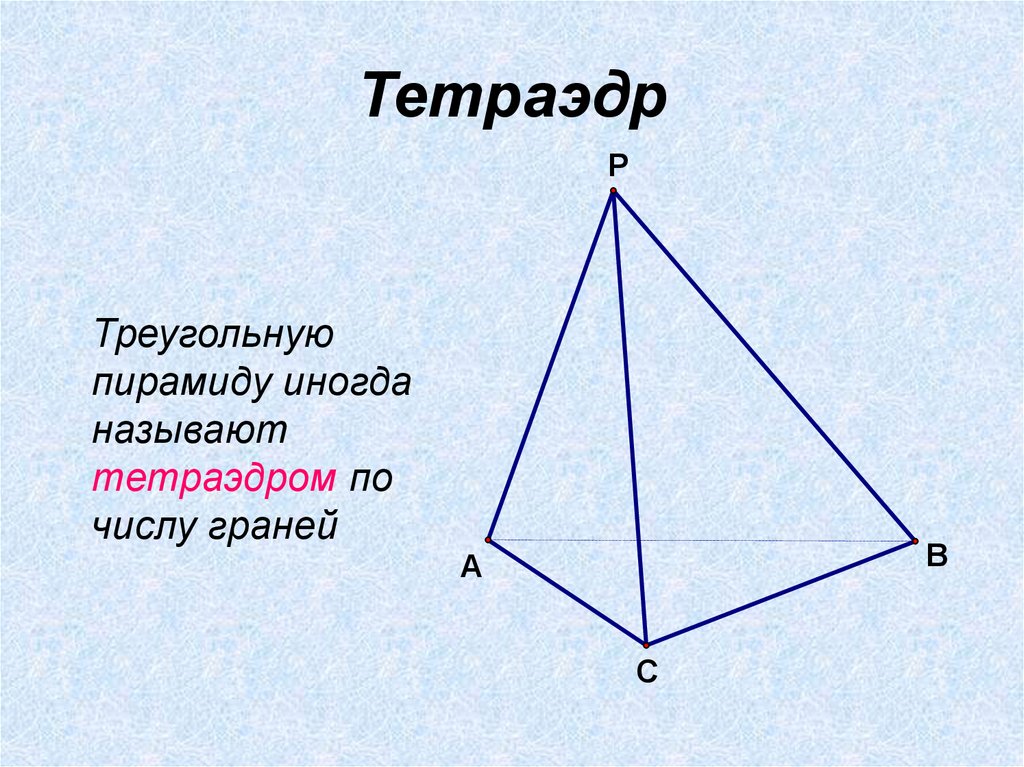
8. Тетраэдр

P
Треугольную
пирамиду иногда
называют
тетраэдром по
числу граней
B
A
C

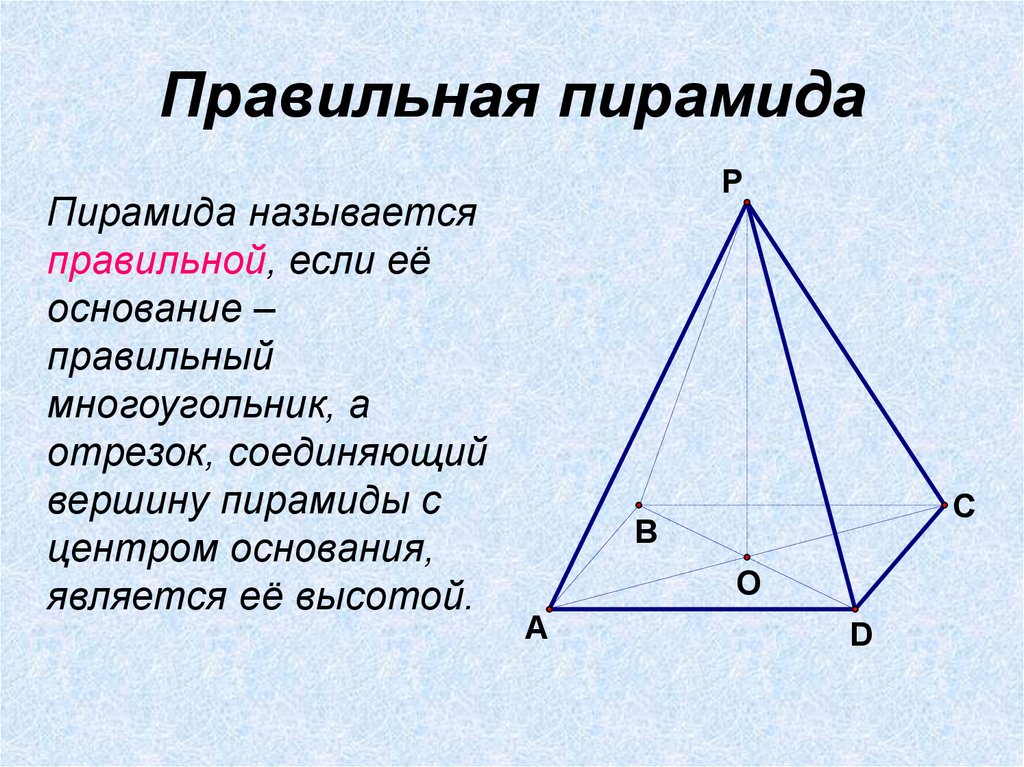
9. Правильная пирамида

Пирамида называется
правильной, если её
основание –
правильный
многоугольник, а
отрезок, соединяющий
вершину пирамиды с
центром основания,
является её высотой.
P
C
B
O
A
D

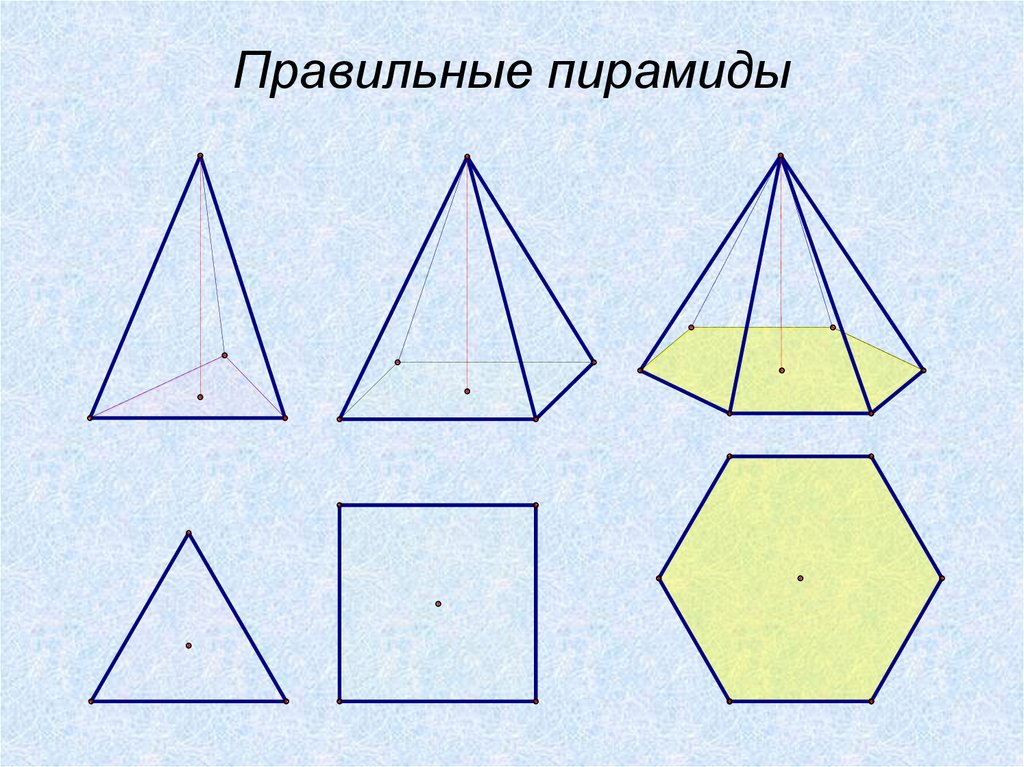
10. Правильные пирамиды

11. Свойства боковых ребер и боковых граней правильной пирамиды

P
C
B
O
A
D
Все боковые ребра
правильной
пирамиды равны, а
боковые грани
являются равными
равнобедренными
треугольниками

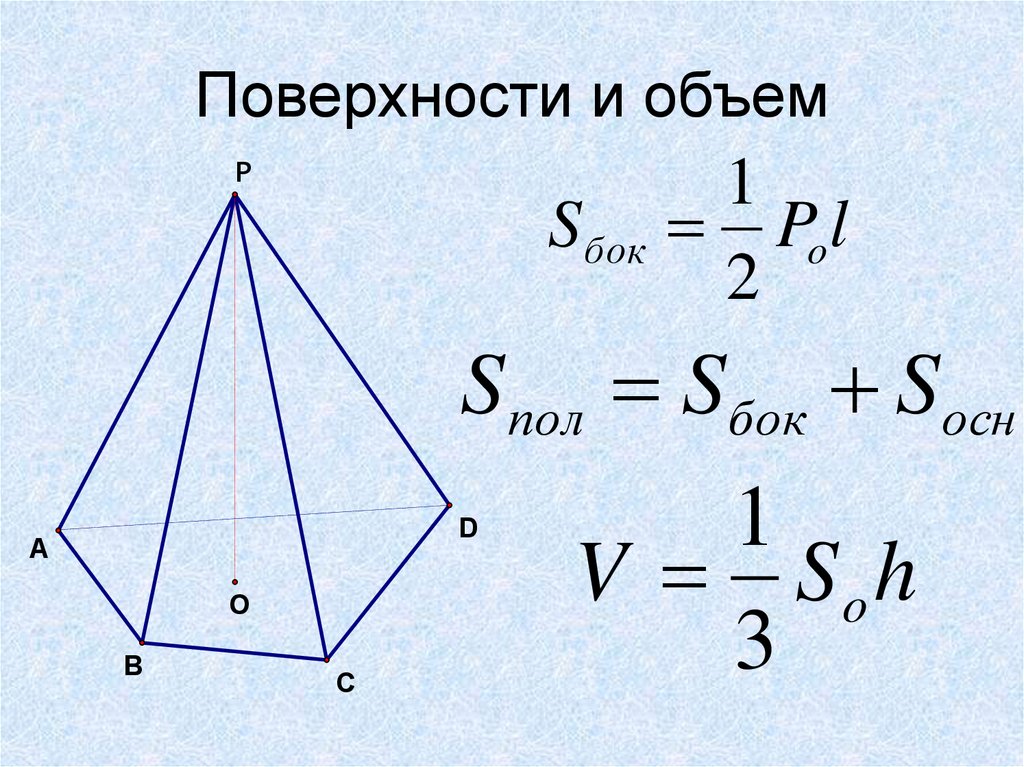
12. Поверхности и объем

P
S бок
1
Pol
2
S пол Sбок Sосн
D
A
O
B
C
1
V So h
3

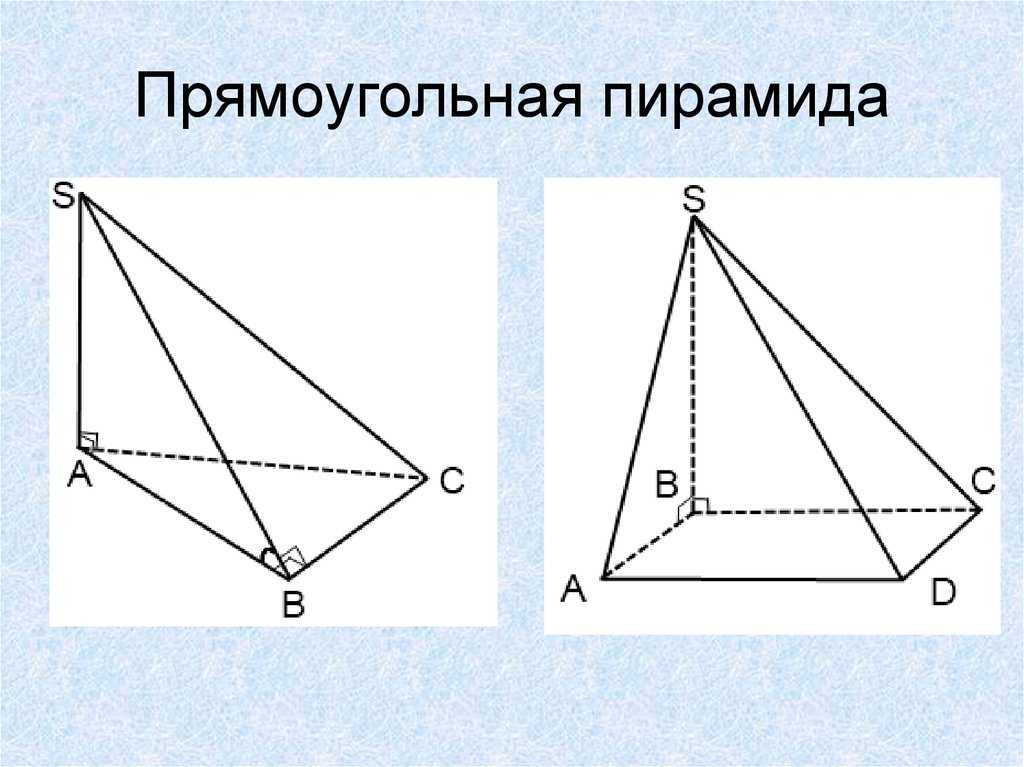
13. Прямоугольная пирамида

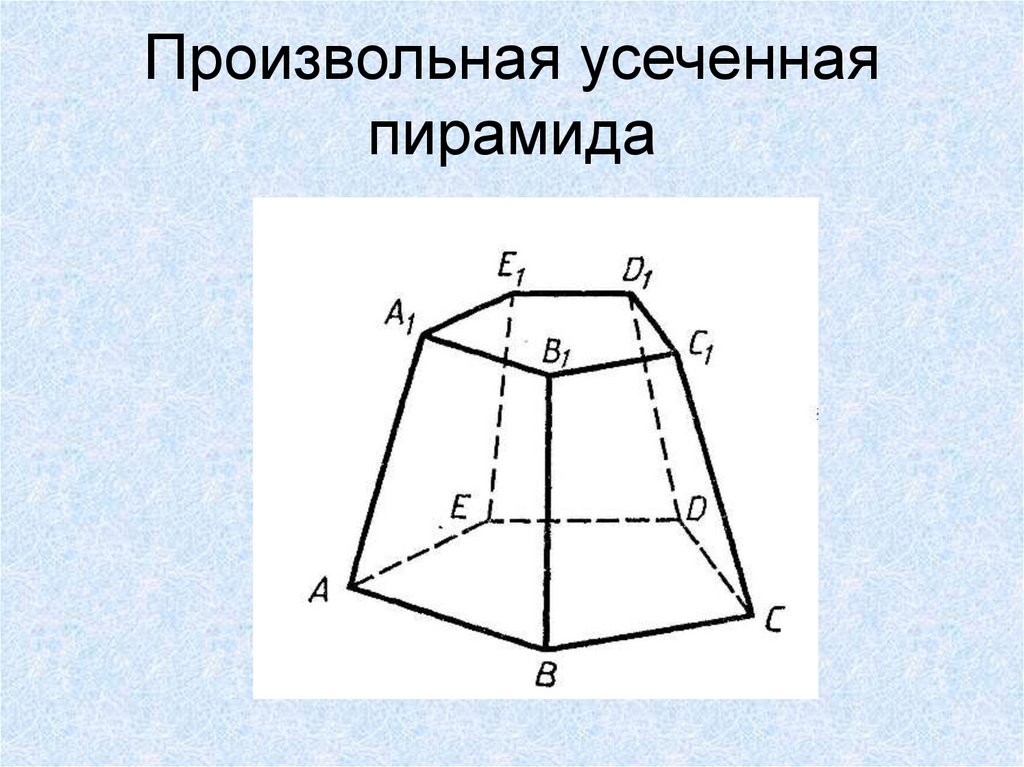
14. Произвольная усеченная пирамида

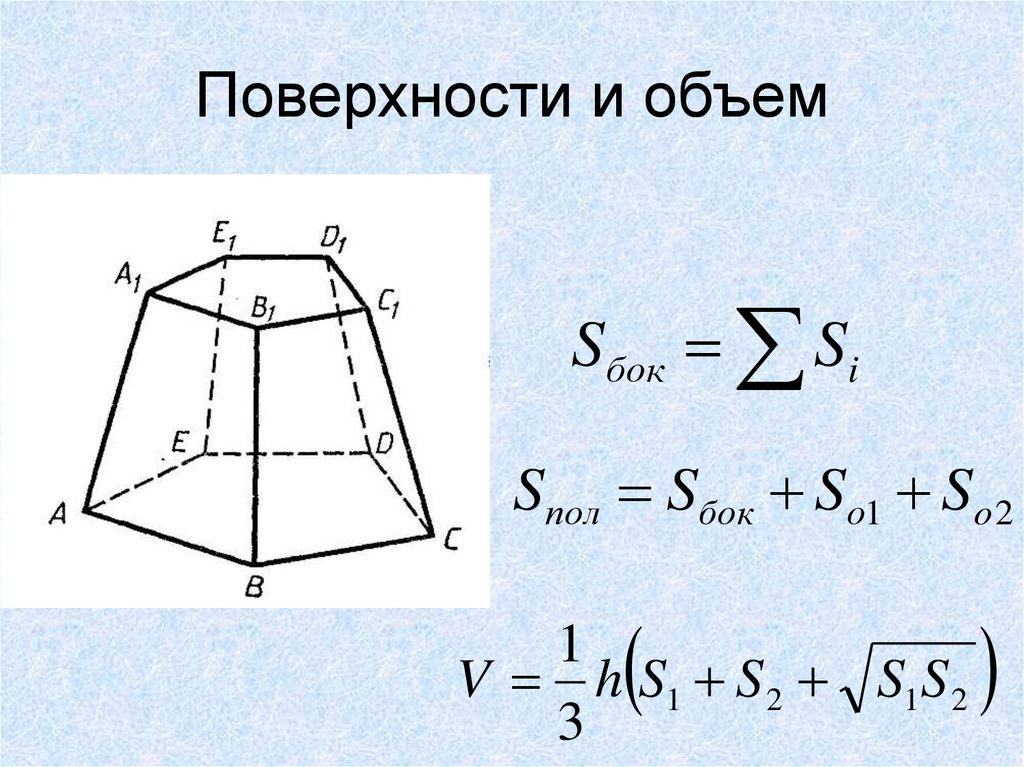
15. Поверхности и объем

Sбок Si
Sпол Sбок Sо1 So 2
1
V h S1 S 2 S1S 2
3

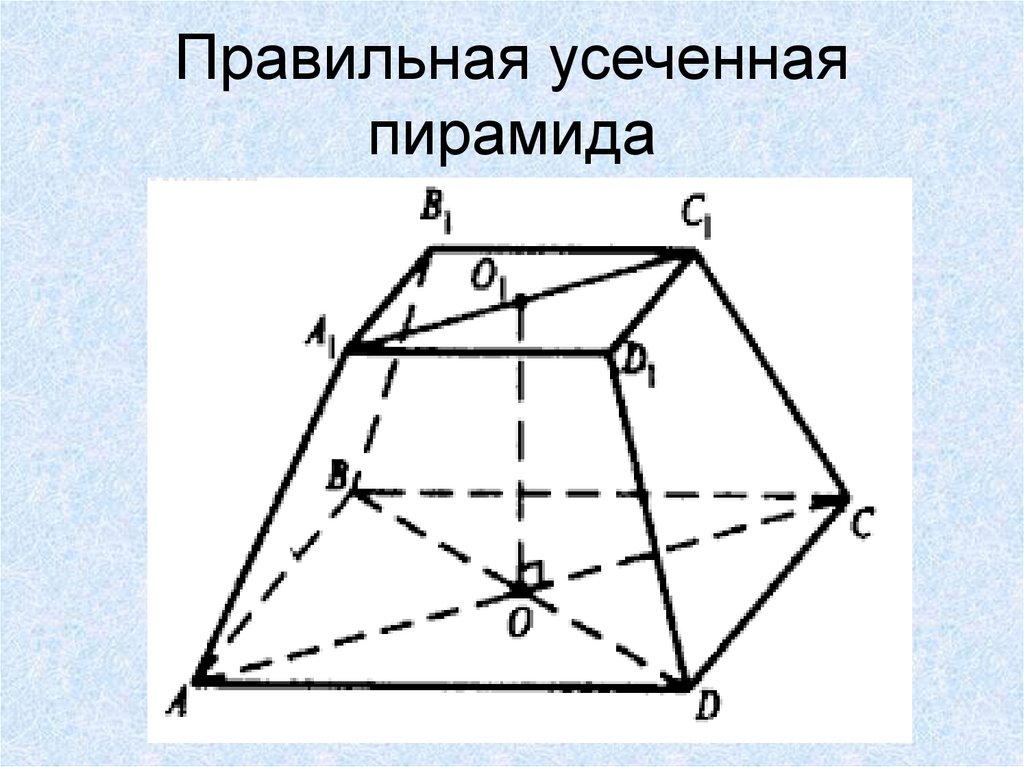
16. Правильная усеченная пирамида

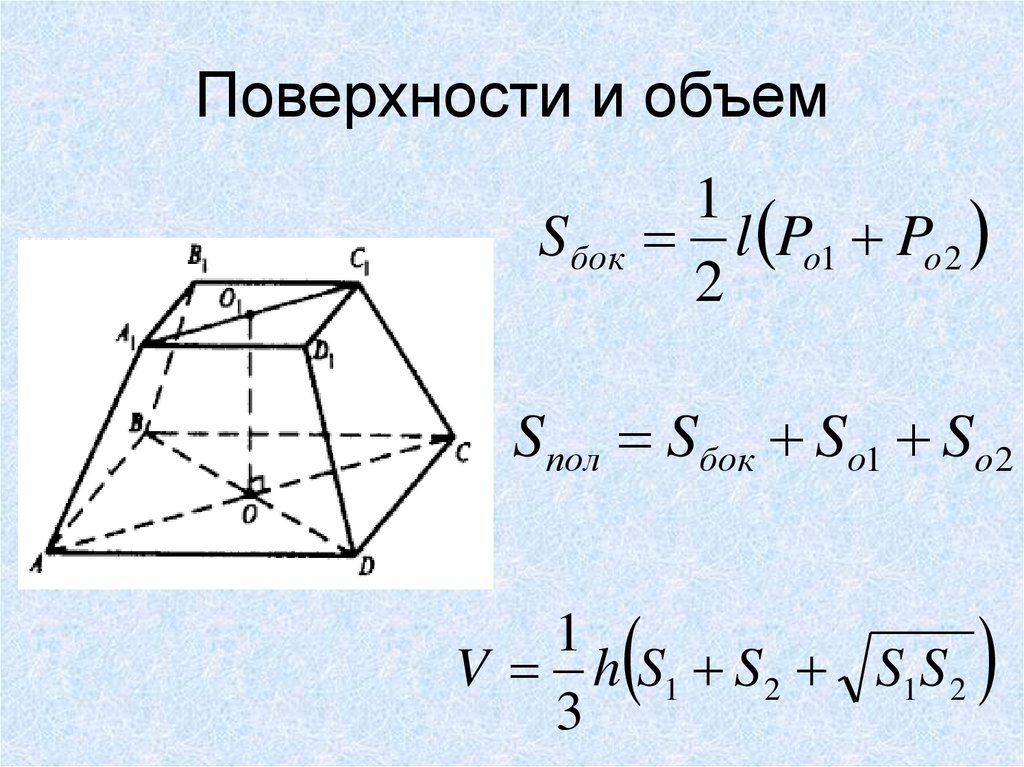
17. Поверхности и объем

S бок
1
l Po1 Po 2
2
Sпол Sбок Sо1 So 2
1
V h S1 S 2 S1S 2
3