Similar presentations:
Пирамиды древности
1. Пирамида
2. Пирамиды древности
3. Примеры пирамид
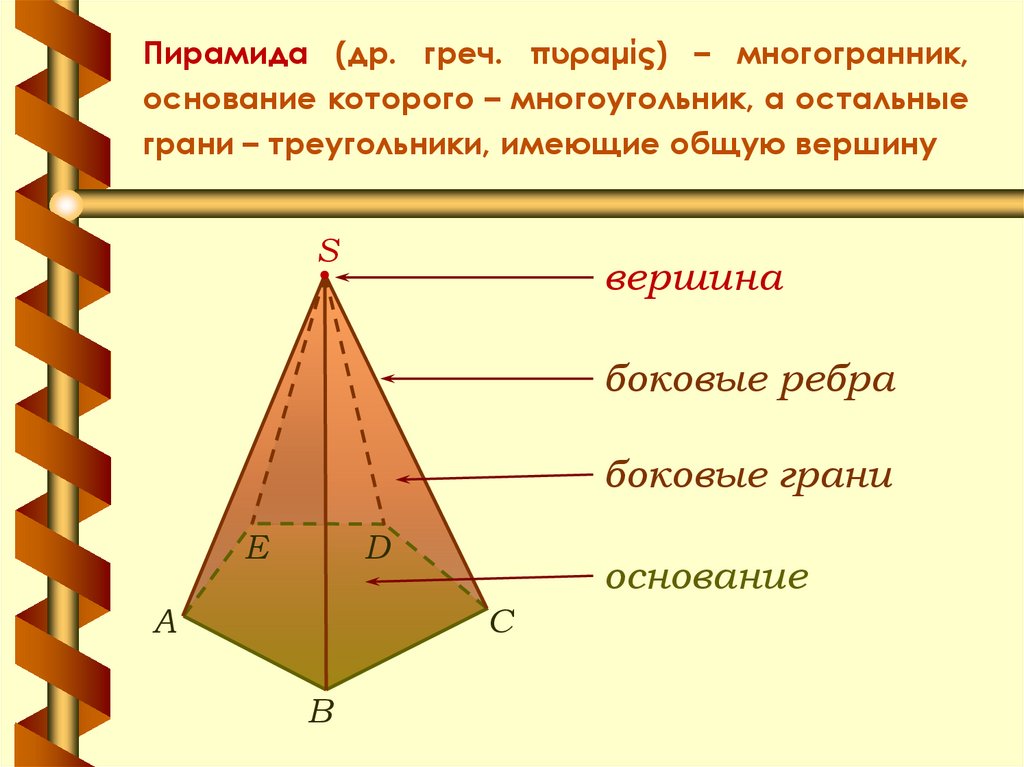
4. Пирамида (др. греч. πυραμίς) – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие
Пирамида (др. греч. πυραμίς) – многогранник,основание которого – многоугольник, а остальные
грани – треугольники, имеющие общую вершину
S
вершина
боковые ребра
боковые грани
D
E
А
основание
C
B
5. Виды пирамид
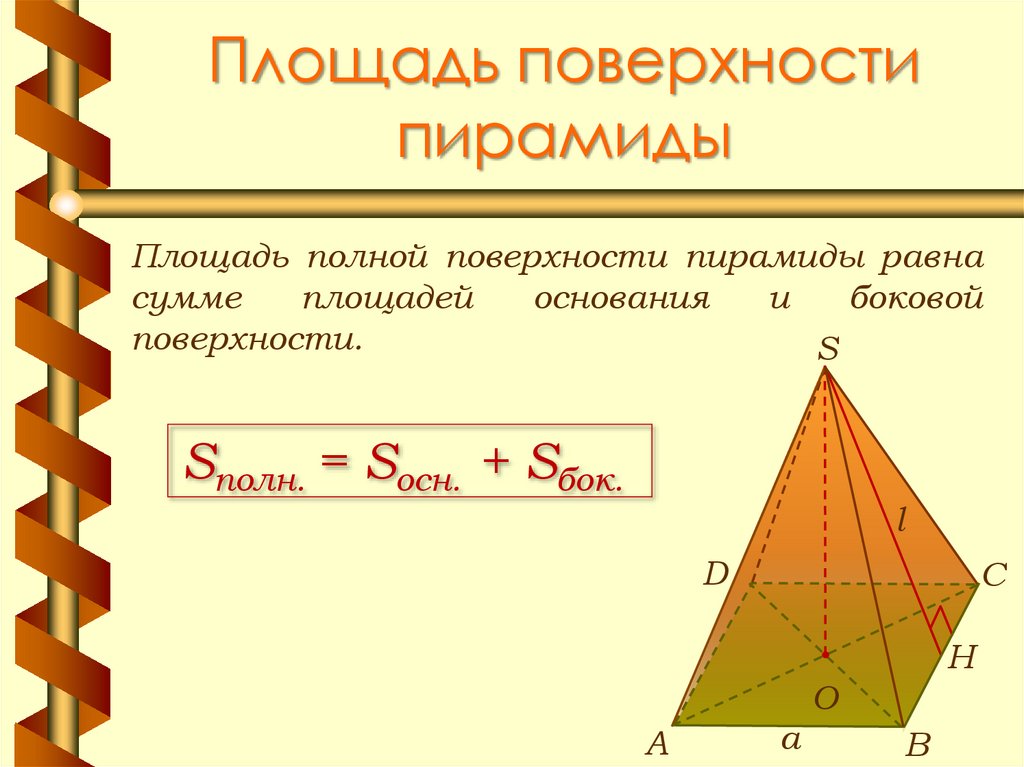
6. Площадь поверхности пирамиды
Площадь полной поверхности пирамиды равнасумме
площадей
основания
и
боковой
поверхности.
S
Sполн. = Sосн. + Sбок.
l
D
С
Н
А
а
О
В
7.
Пирамида называется правильной, если основаниемеё является правильный многоугольник, а вершина
проецируется в центр основания.
S
В правильной пирамиде
все боковые грани –
равные равнобедренные
треугольники.
D
С
Н
О
А
В
Апофема – высота
боковой грани
правильной
пирамиды.
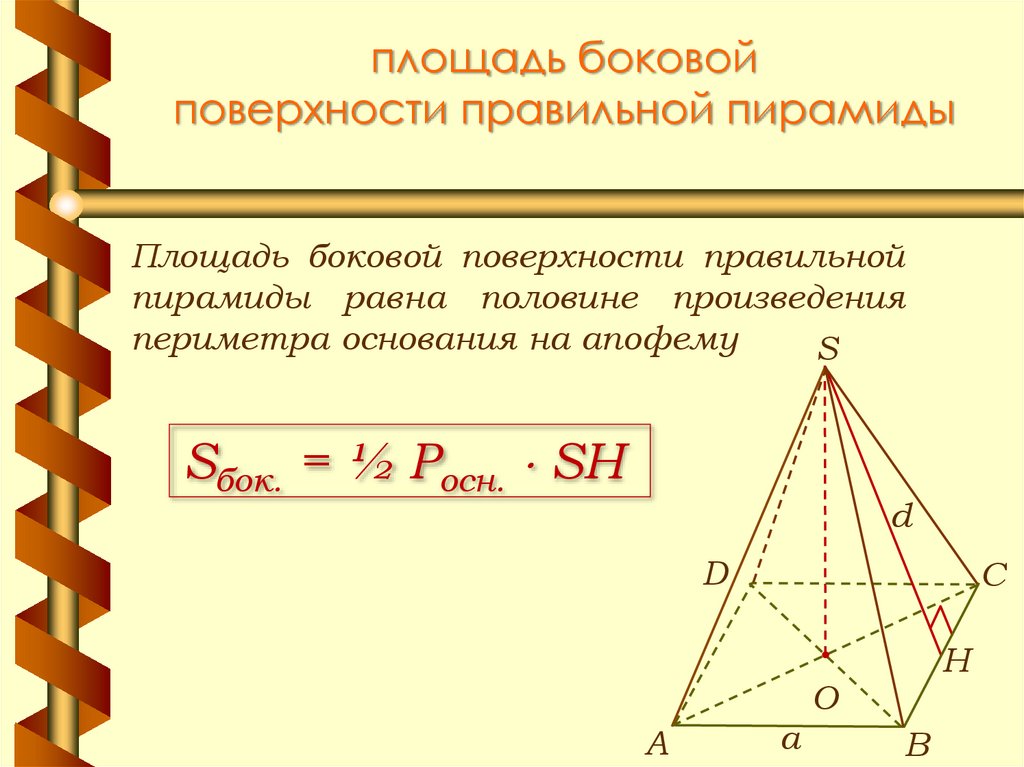
8. площадь боковой поверхности правильной пирамиды
Площадь боковой поверхности правильнойпирамиды равна половине произведения
периметра основания на апофему
S
Sбок. = ½ Pосн. SH
d
D
А
С
а
Н
О
В
9. Объем пирамиды
Объем пирамиды равен 1/3 произведенияплощади основания на высоту.
S
Vпир. = 1/3 Sосн h
h
D
А
С
а
О
В
10. Построение правильных пирамид
SS
S
D
А
C
M
O
С
А
M
В
F
A
B
В
E
D
O
C
M
O
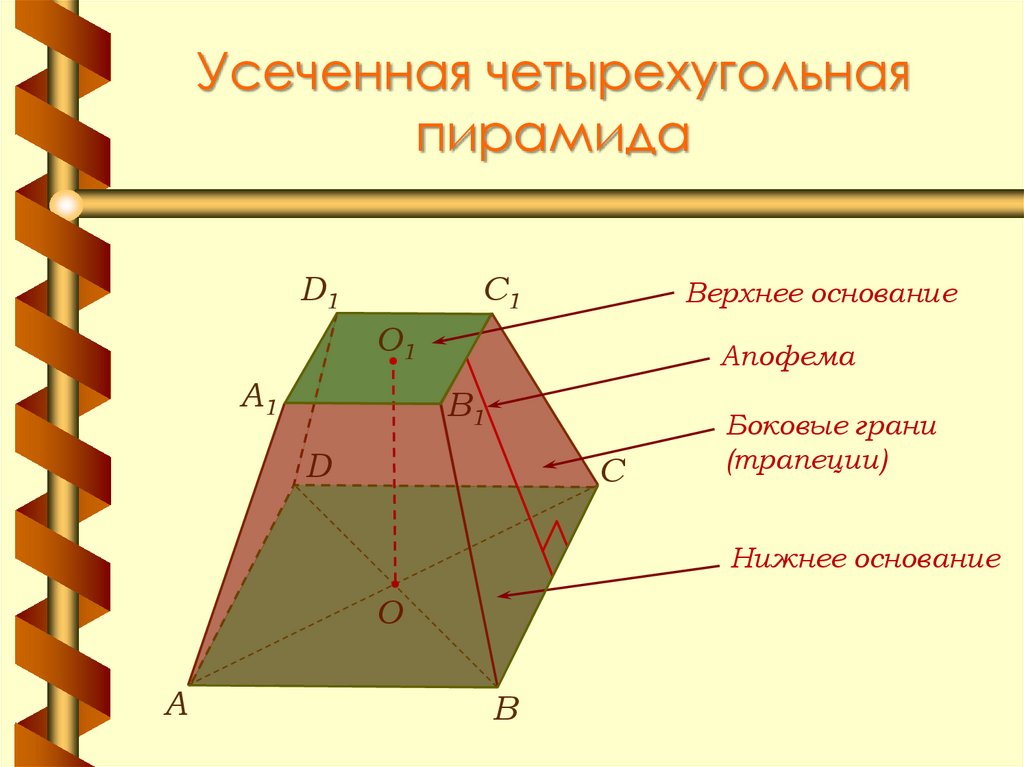
11. Усеченная четырехугольная пирамида
D1C1
Верхнее основание
О1
A1
Апофема
B1
D
С
Боковые грани
(трапеции)
Нижнее основание
О
А
В
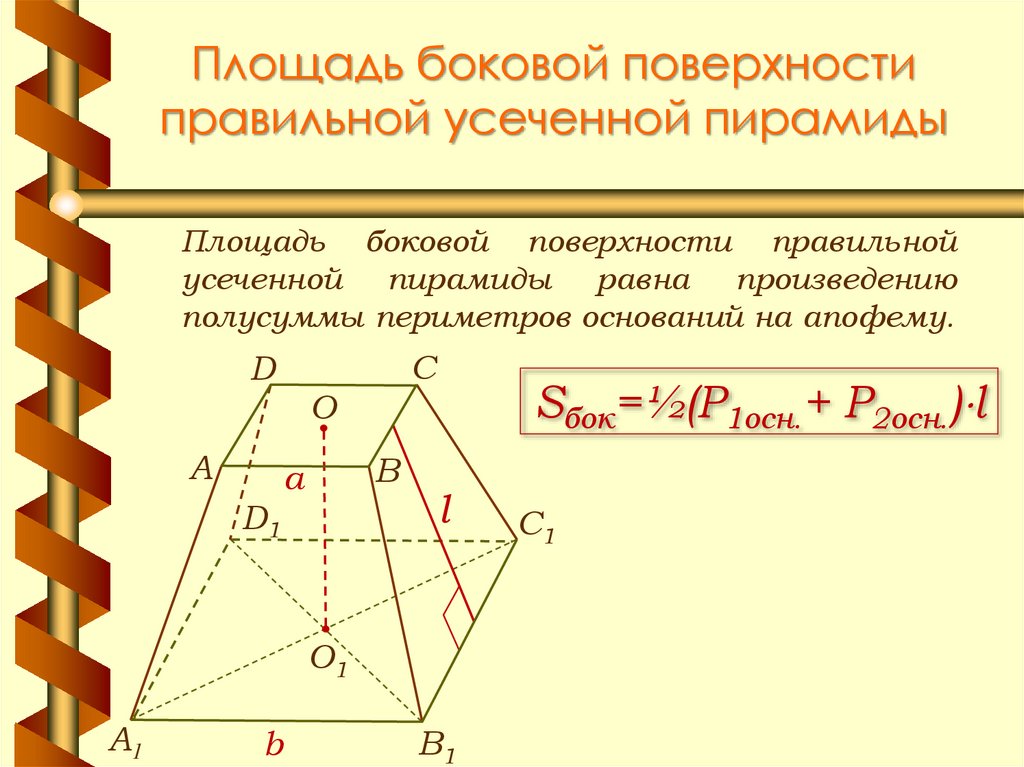
12. Площадь боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильнойусеченной пирамиды равна произведению
полусуммы периметров оснований на апофему.
D
A
D1
C
О
B
a
Sбок=½(P1осн.+ P2осн.) l
l
О1
А1
b
В1
С1






 mathematics
mathematics








