Пирамида

1.

2.

«Пирос» по-гречески
рожь. Считают, что
греки выпекали
хлебцы, имевшие
форму пирамиды.
Слово «пирамида» в геометрию ввели греки,
которые, как полагают, заимствовали его у египтян,
создавших самые знаменитые пирамиды на свете.

3. Пирамида

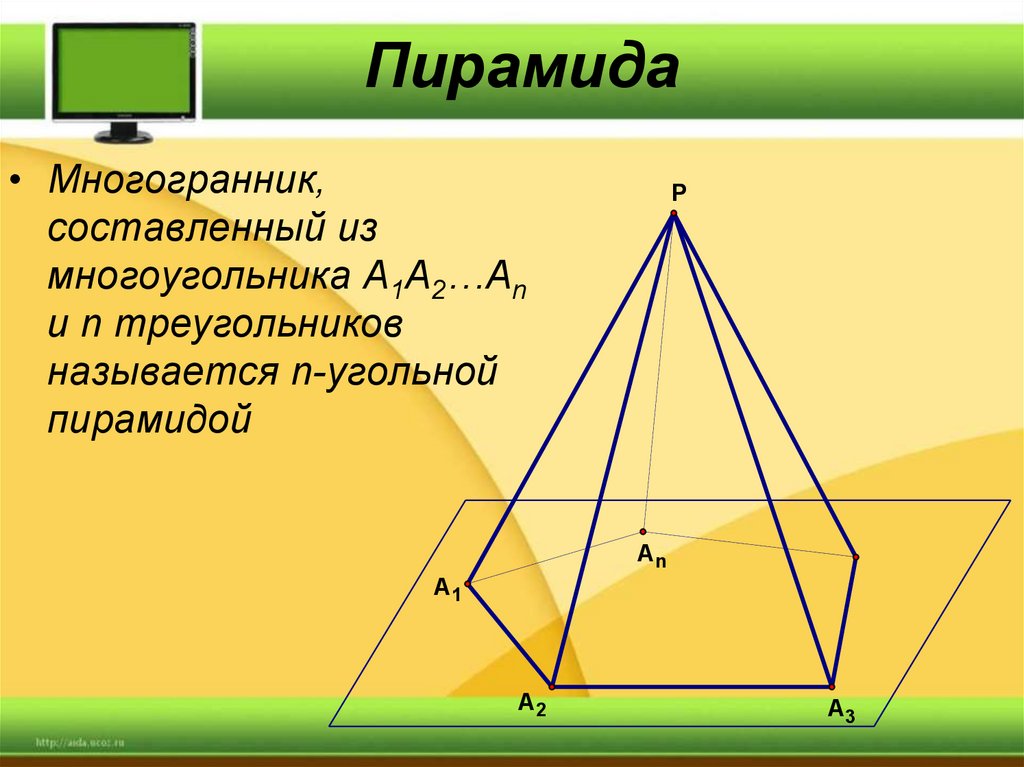
• Многогранник,
составленный из
многоугольника A1A2…An
и n треугольников
называется n-угольной
пирамидой
P
An
A1
A2
A3

4.

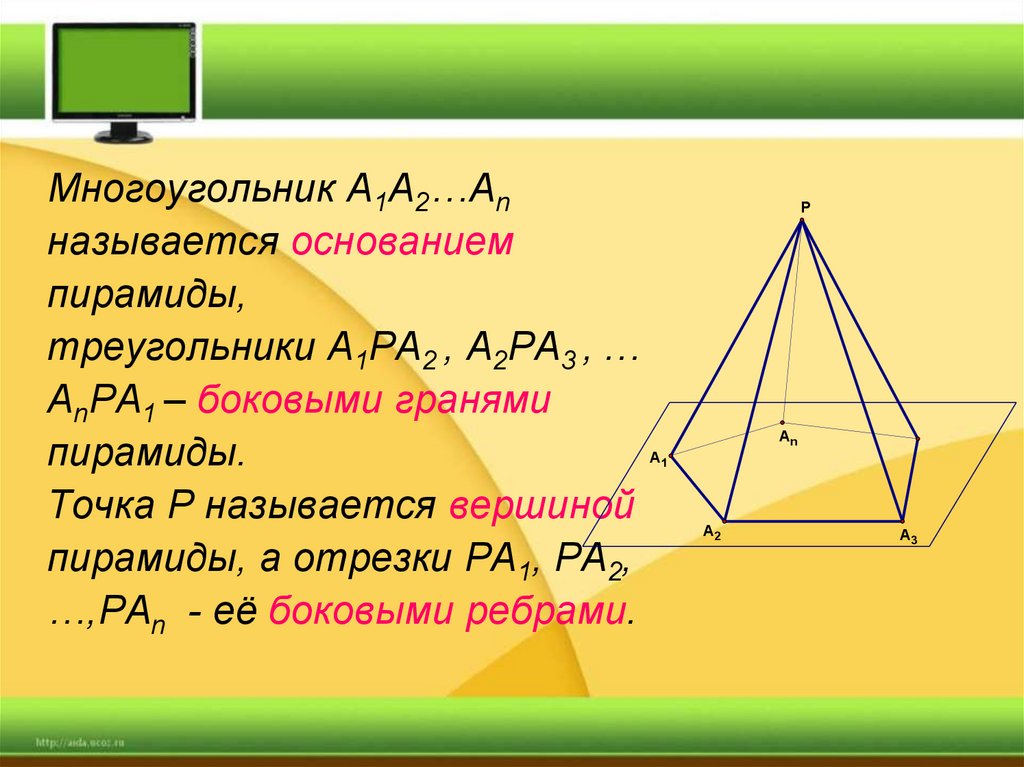
Многоугольник A1A2…An
называется основанием
пирамиды,
треугольники A1PA2 , A2PA3 , …
AnPA1 – боковыми гранями
пирамиды.
Точка P называется вершиной
пирамиды, а отрезки PA1, PA2,
…,PAn - её боковыми ребрами.
P
An
A1
A2
A3

5.

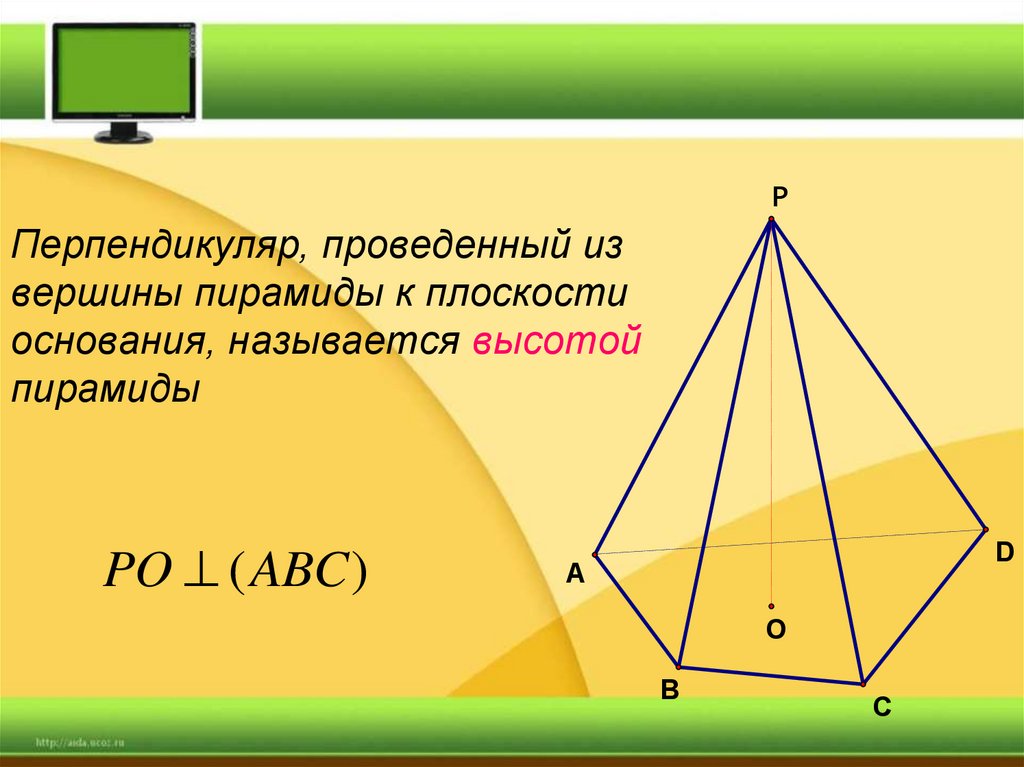
P
Перпендикуляр, проведенный из
вершины пирамиды к плоскости
основания, называется высотой
пирамиды
PO ( ABC )
D
A
O
B
C

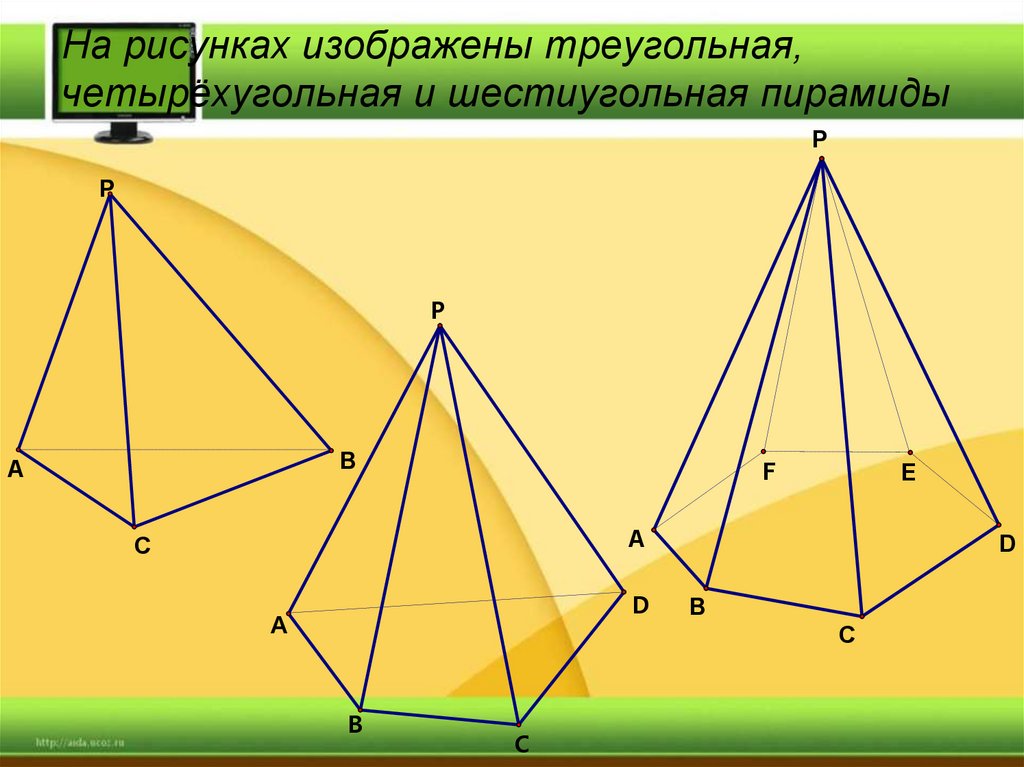
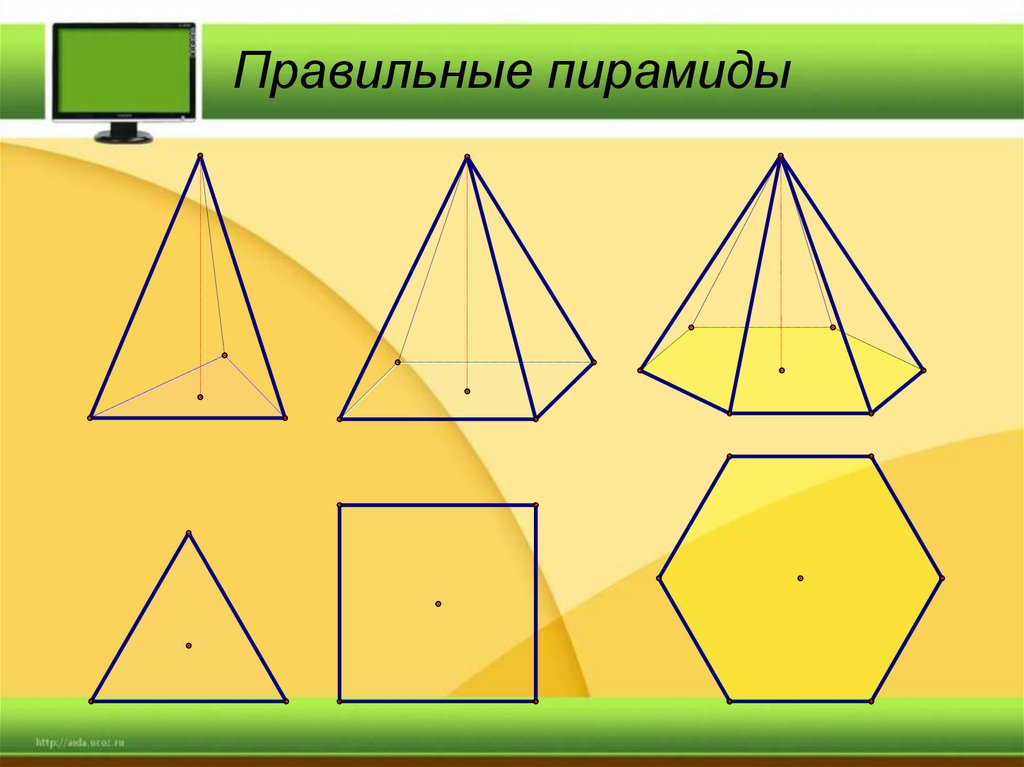
6. На рисунках изображены треугольная, четырёхугольная и шестиугольная пирамиды

P
P
P
B
A
F
E
A
C
D
A
D
B
C
B
C

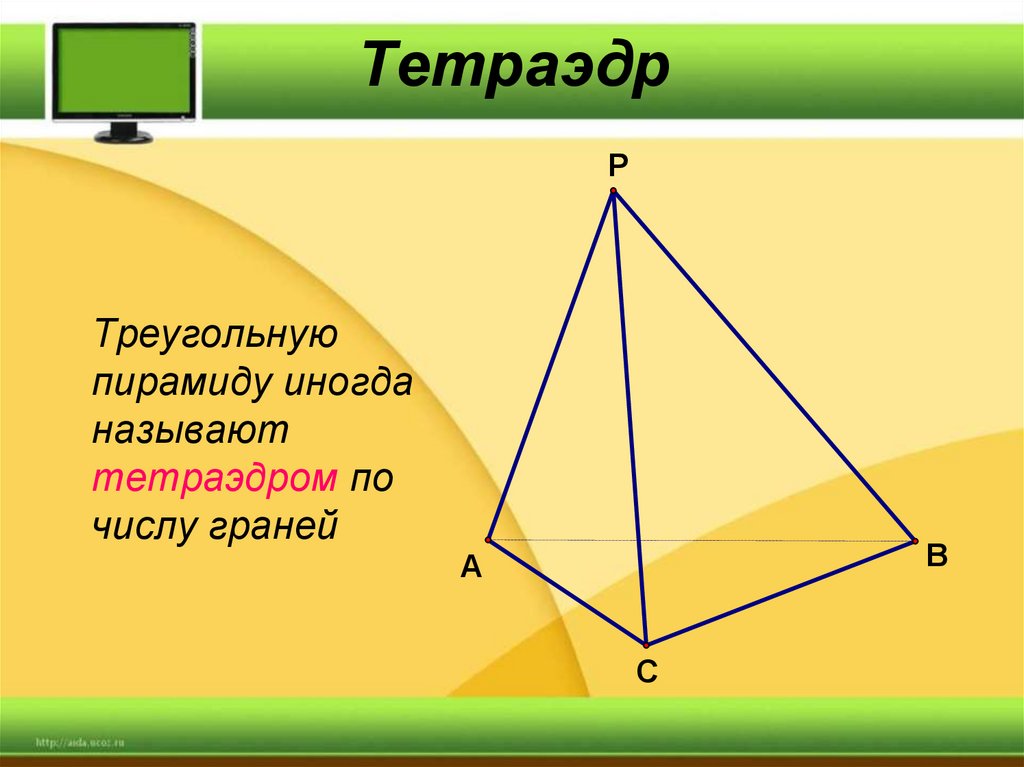
7. Тетраэдр

P
Треугольную
пирамиду иногда
называют
тетраэдром по
числу граней
B
A
C

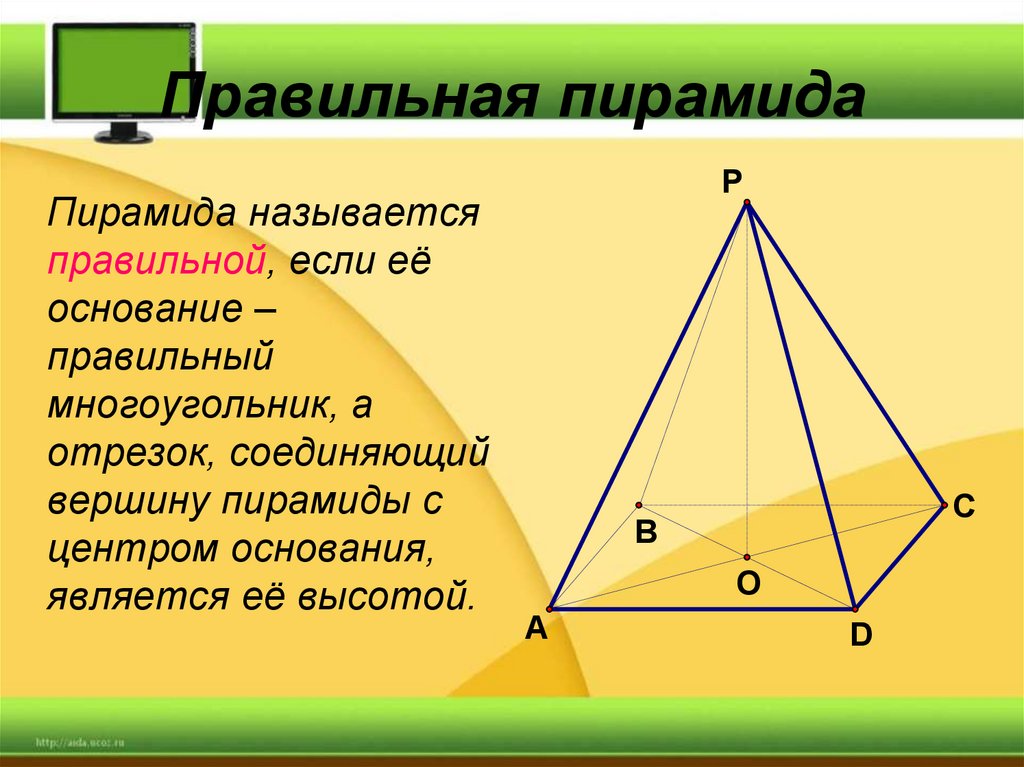
8. Правильная пирамида

Пирамида называется
правильной, если её
основание –
правильный
многоугольник, а
отрезок, соединяющий
вершину пирамиды с
центром основания,
является её высотой.
P
C
B
O
A
D

9.

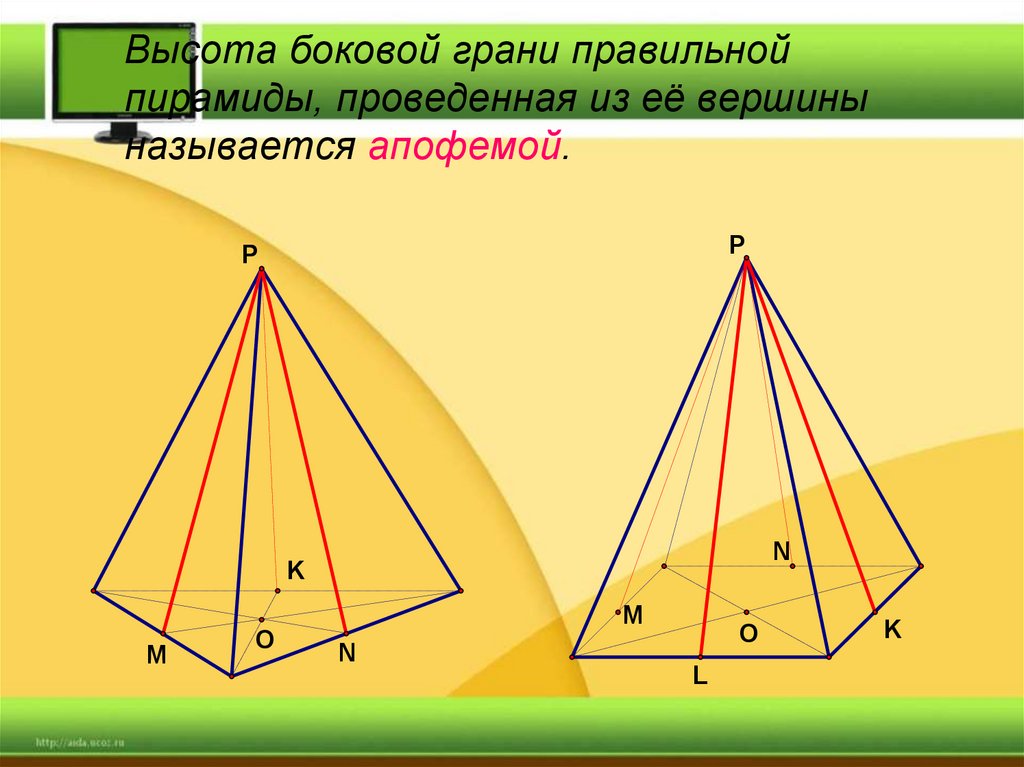
Высота боковой грани правильной
пирамиды, проведенная из её вершины
называется апофемой.
P
P
N
K
M
M
O
N
O
L
K

10. Правильные пирамиды

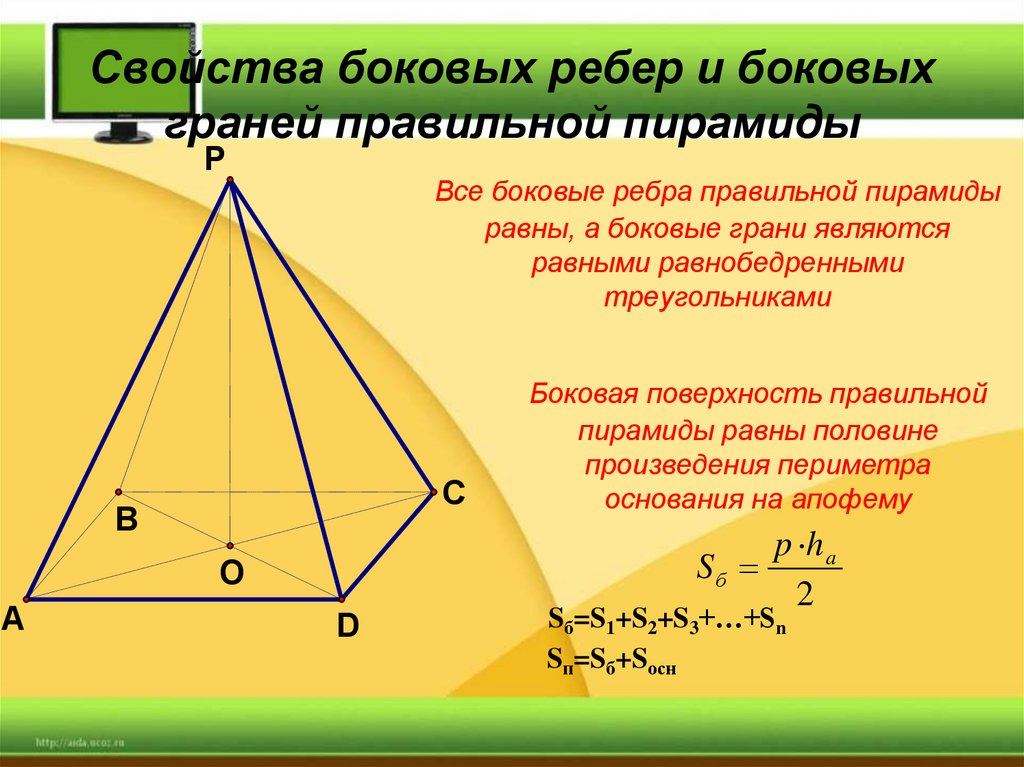
11. Свойства боковых ребер и боковых граней правильной пирамиды

P
Все боковые ребра правильной пирамиды
равны, а боковые грани являются
равными равнобедренными
треугольниками
C
B
O
A
D
Боковая поверхность правильной
пирамиды равны половине
произведения периметра
основания на апофему
p h a
Sб
2
Sб=S1+S2+S3+…+Sn
Sп=Sб+Sосн

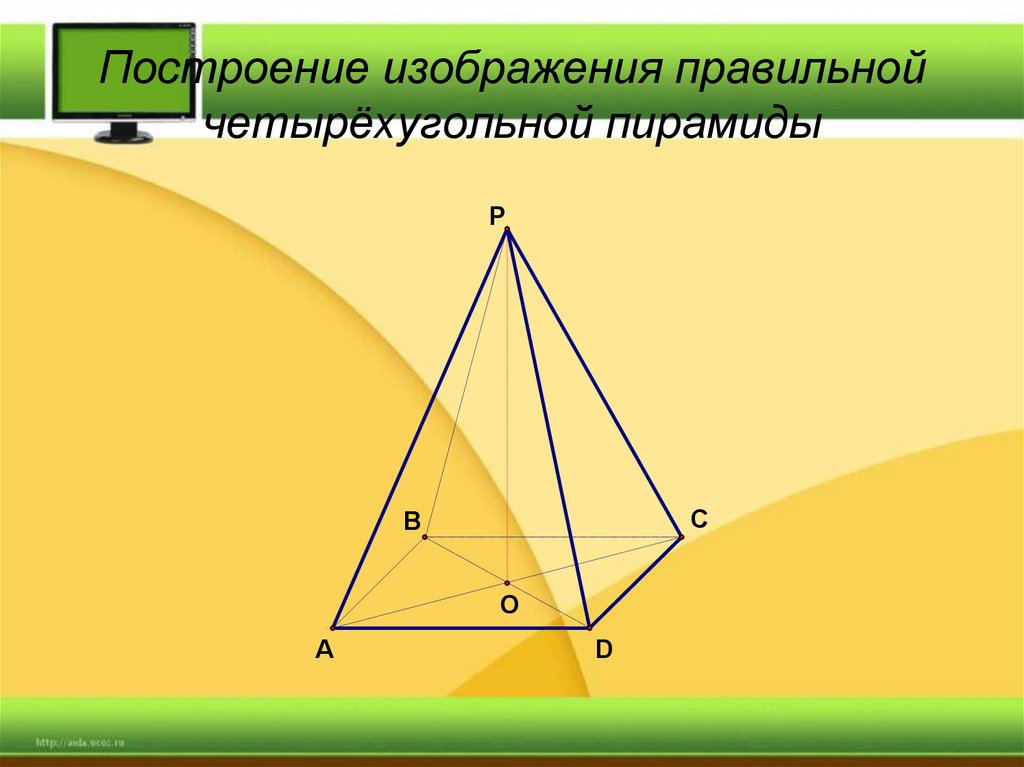
12. Построение изображения правильной четырёхугольной пирамиды

13. Построение изображения правильной четырёхугольной пирамиды

14. Построение изображения правильной четырёхугольной пирамиды

15. Построение изображения правильной четырёхугольной пирамиды

16. Построение изображения правильной четырёхугольной пирамиды

17. Построение изображения правильной четырёхугольной пирамиды

18. Построение изображения правильной четырёхугольной пирамиды

19. Построение изображения правильной четырёхугольной пирамиды

20. Построение изображения правильной четырёхугольной пирамиды

21. Построение изображения правильной четырёхугольной пирамиды

22. Построение изображения правильной четырёхугольной пирамиды

23. Построение изображения правильной четырёхугольной пирамиды

24. Построение изображения правильной четырёхугольной пирамиды

P
C
B
O
A
D

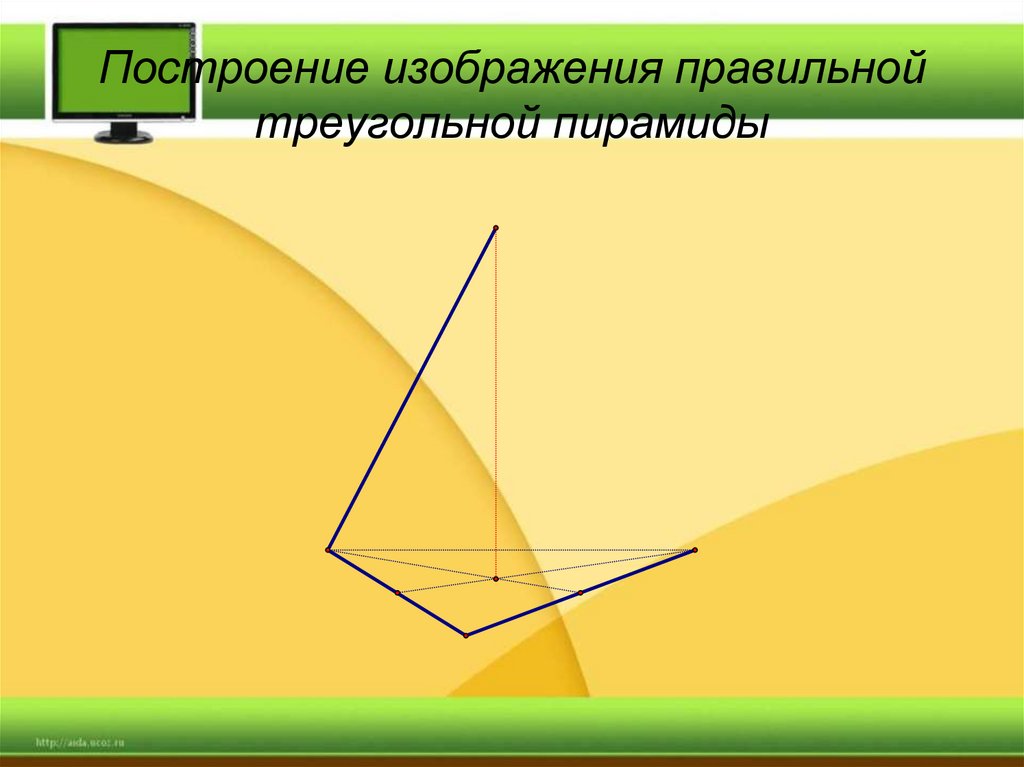
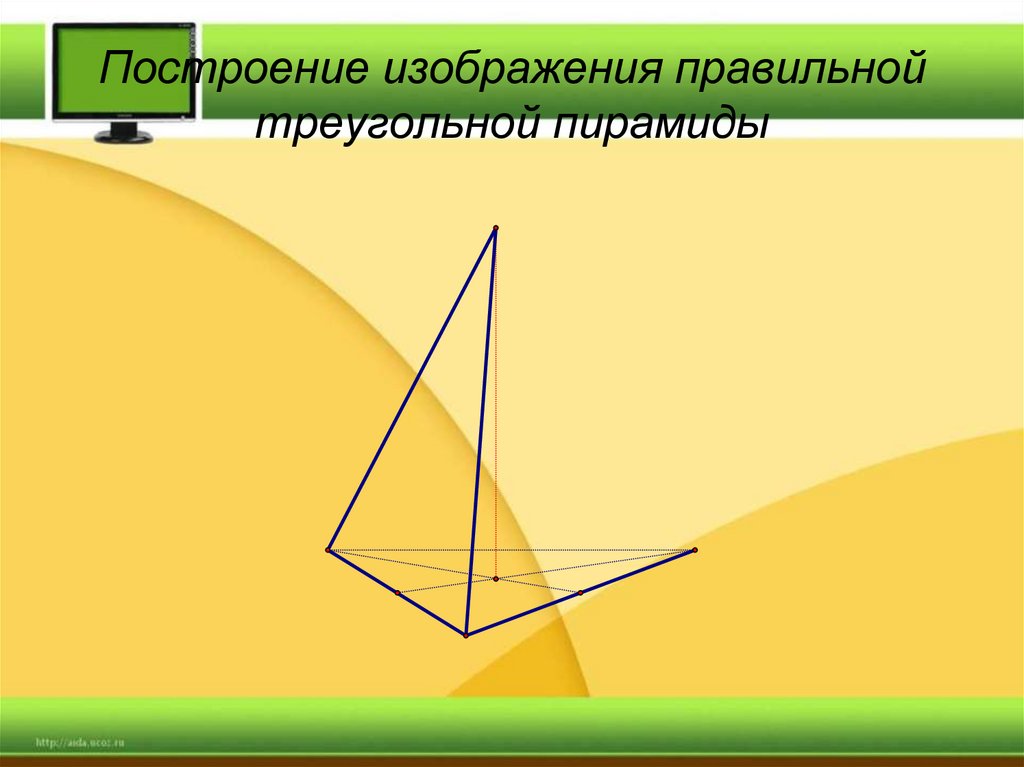
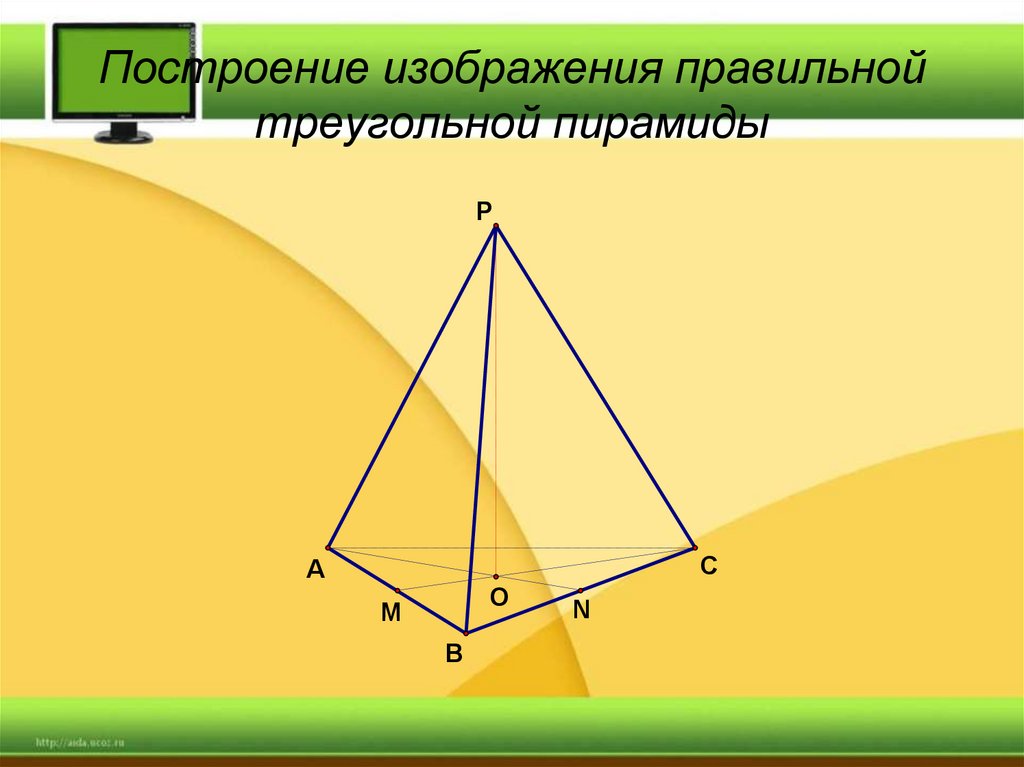
25. Построение изображения правильной треугольной пирамиды

26. Построение изображения правильной треугольной пирамиды

27. Построение изображения правильной треугольной пирамиды

28. Построение изображения правильной треугольной пирамиды

29. Построение изображения правильной треугольной пирамиды

30. Построение изображения правильной треугольной пирамиды

31. Построение изображения правильной треугольной пирамиды

32. Построение изображения правильной треугольной пирамиды

33. Построение изображения правильной треугольной пирамиды

34. Построение изображения правильной треугольной пирамиды

35. Построение изображения правильной треугольной пирамиды

36. Построение изображения правильной треугольной пирамиды

37. Построение изображения правильной треугольной пирамиды

P
C
A
O
M
B
N

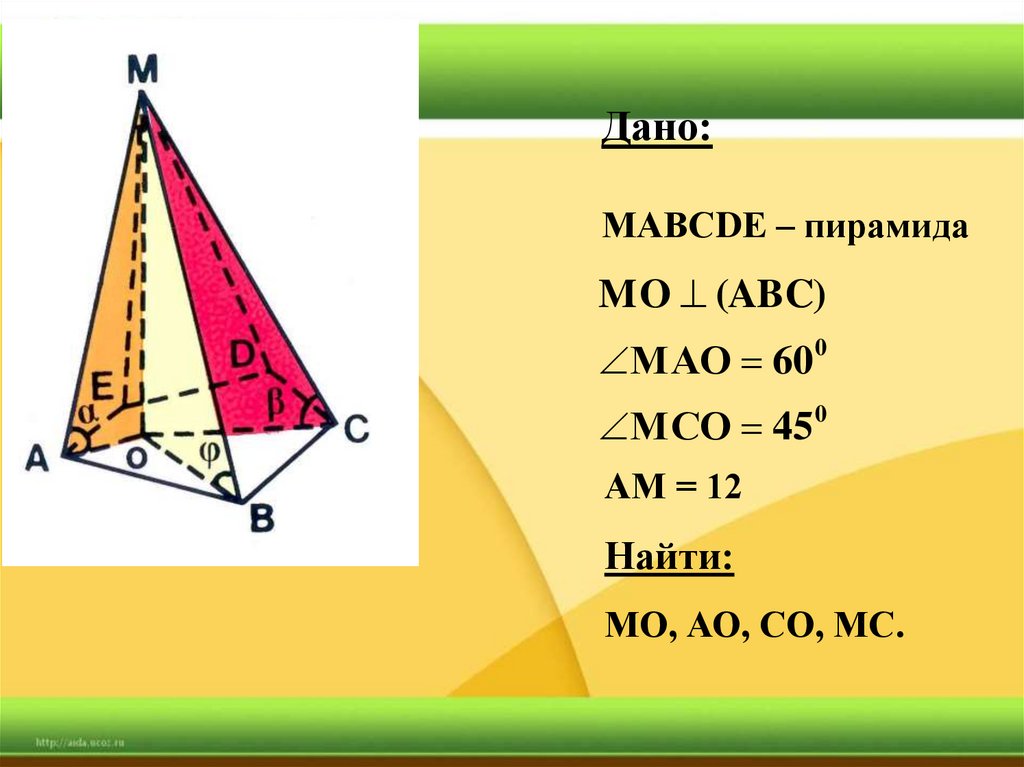
38.

Дано:
МАВСDЕ – пирамида
MO (ABC)
МАО 60 0
МСО 45 0
АМ = 12
Найти:
МО, АО, СО, МС.

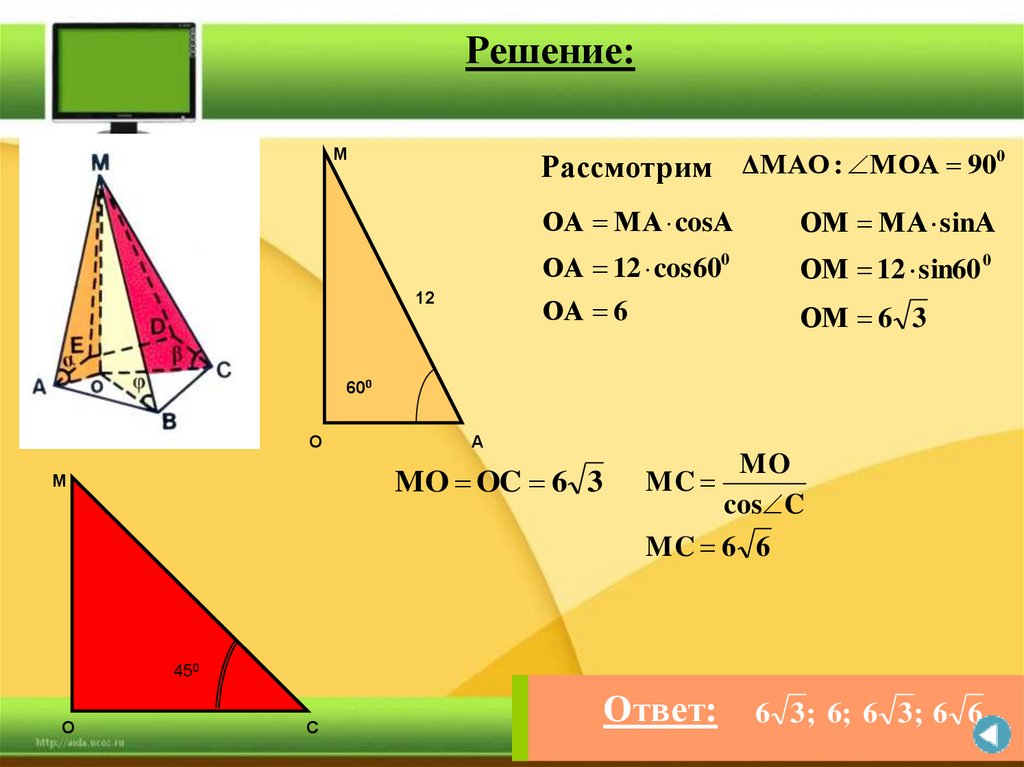
39.

Решение:
М
Рассмотрим ΔMAO : МОА 900
12
ОА МА cosА
ОМ МА sinА
ОА 12 cos600
ОМ 12 sin60 0
ОА 6
ОМ 6 3
600
О
А
MO OC 6 3
М
MO
cos C
MC 6 6
MC
450
О
С
Ответ:
6 3 ; 6; 6 3 ; 6 6

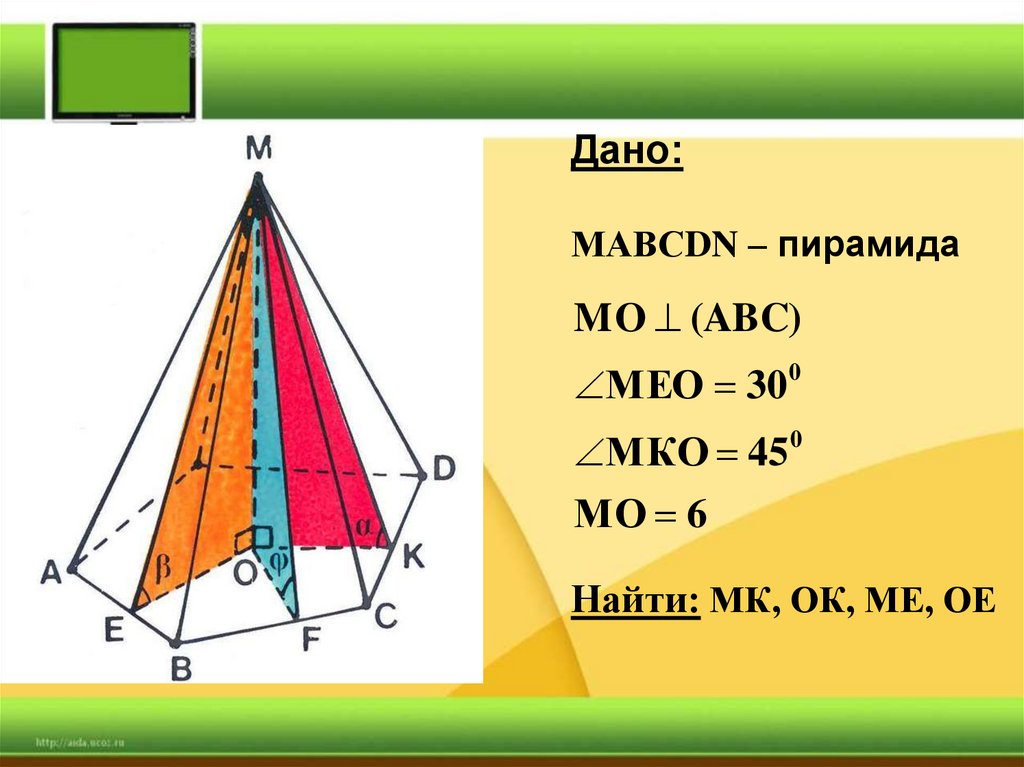
40.

Дано:
МАВСDN – пирамида
MO (ABC)
МЕО 30
0
МКО 45 0
МО 6
Найти: МК, ОК, МЕ, ОЕ

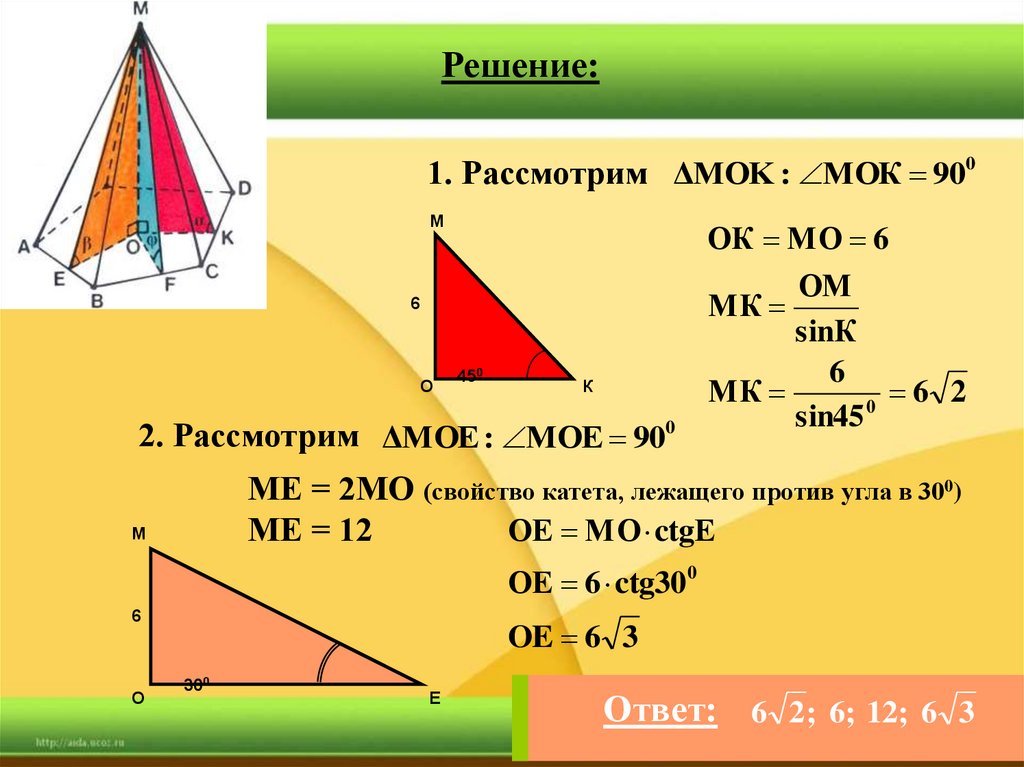
41.

Решение:
1. Рассмотрим ΔMOK : МОК 900
М
ОК МО 6
ОМ
sinК
6
МК
6 2
0
sin45
МК
6
О
450
К
2. Рассмотрим ΔMOE : МОЕ 900
МЕ = 2МО (свойство катета, лежащего против угла в 300)
МЕ = 12
ОЕ МО ctgЕ
М
ОЕ 6 ctg30 0
6
О
OE 6 3
300
Е
Ответ: 6 2 ; 6; 12; 6 3

42. Усеченная пирамида

Плоскость параллельная
основанию пирамиды,
разбивает её на два
многогранника. Один из них
является пирамидой, а другой
называется усечённой
пирамидой.
Усеченная пирамида – это
часть полной пирамиды,
заключенная между её
основанием и секущей
плоскостью, параллельной
основанию данной пирамиды

43. Правильная усеченная пирамида

Усеченная пирамида называется
правильной, если она получена
сечением правильной пирамиды
плоскостью, параллельной
основанию.
Основания - правильные
многоугольники .
Боковые грани – равные
равнобедренные трапеции (?).
Высоты этих трапеций называются
апофемами.

44.

Примеры усеченных пирамид

45.

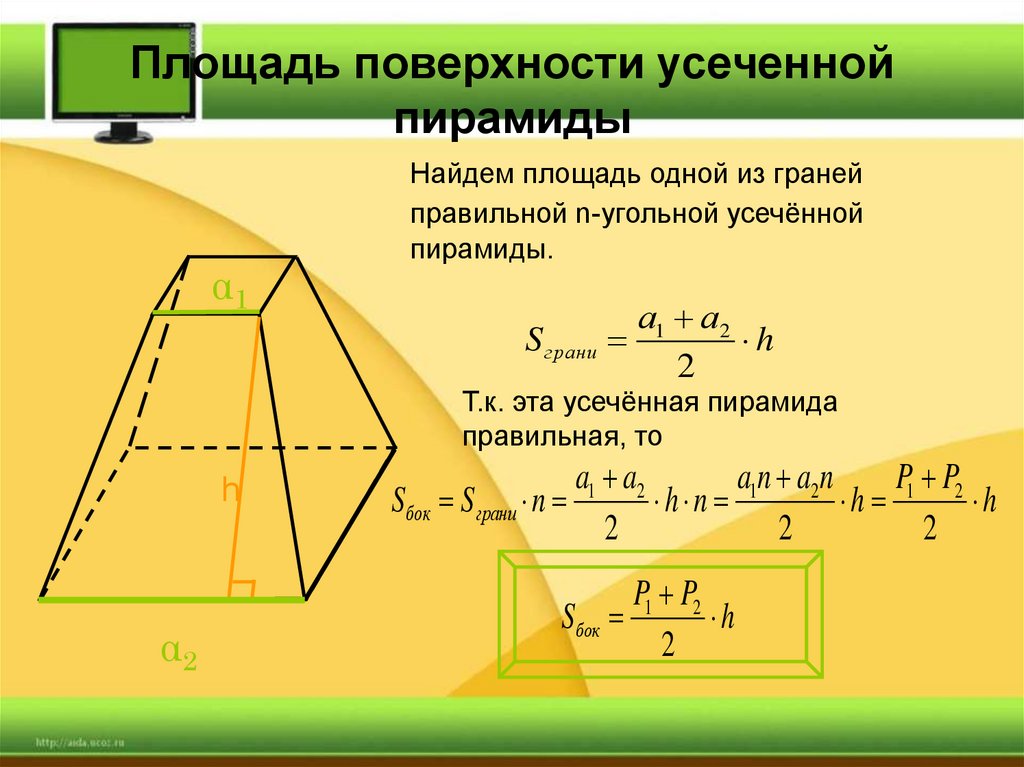
Площадь поверхности усеченной
пирамиды
α1
Найдем площадь одной из граней
правильной n-угольной усечённой
пирамиды.
а1 а2
S грани
h
2
Т.к. эта усечённая пирамида
правильная, то
h
α2
a1 a2
a1n a2n
P1 P2
Sбок Sграни n
h n
h
h
2
2
2
P1 P2
Sбок
h
2

46. Задача

Стороны оснований правильной
треугольной усеченной пирамиды равны
4 см и 2 см, а боковое ребро равно 2 см.
Найдите: 1. апофему пирамиды;
2. площадь полной поверхности.

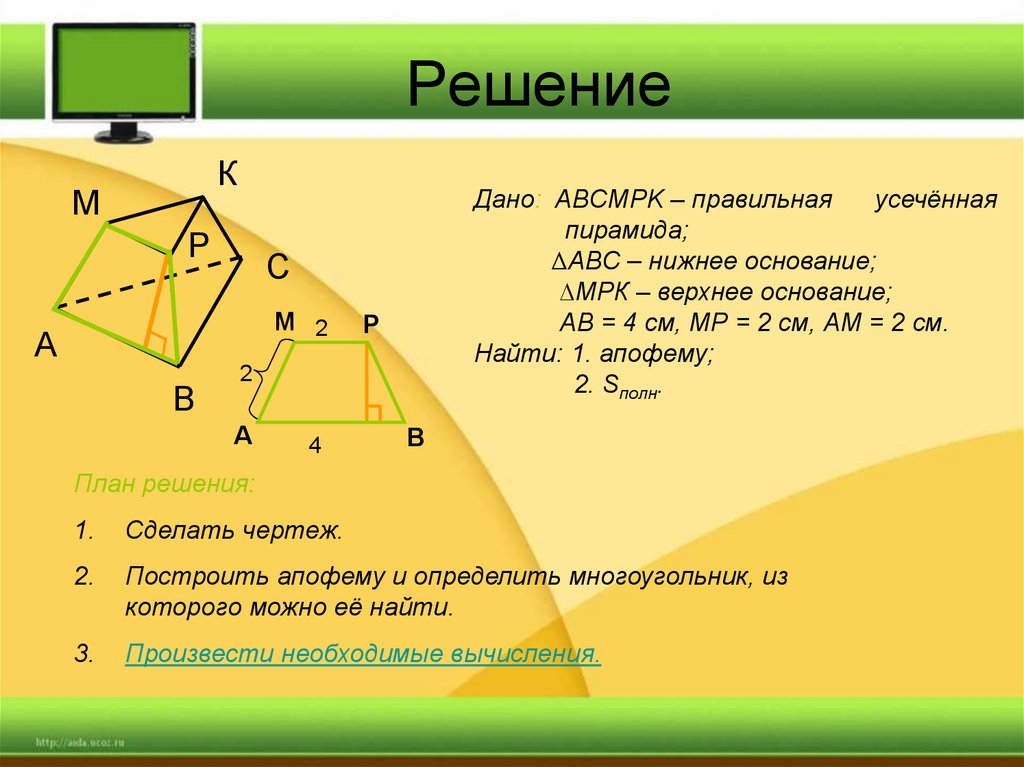
47. Решение

К
М
Р
С
М 2
А
В
Дано: ABCMPK – правильная
усечённая
пирамида;
∆АВС – нижнее основание;
∆МРК – верхнее основание;
АВ = 4 см, МР = 2 см, АМ = 2 см.
Найти: 1. апофему;
2. Sполн.
Р
2
А
4
В
План решения:
1.
Сделать чертеж.
2.
Построить апофему и определить многоугольник, из
которого можно её найти.
3.
Произвести необходимые вычисления.

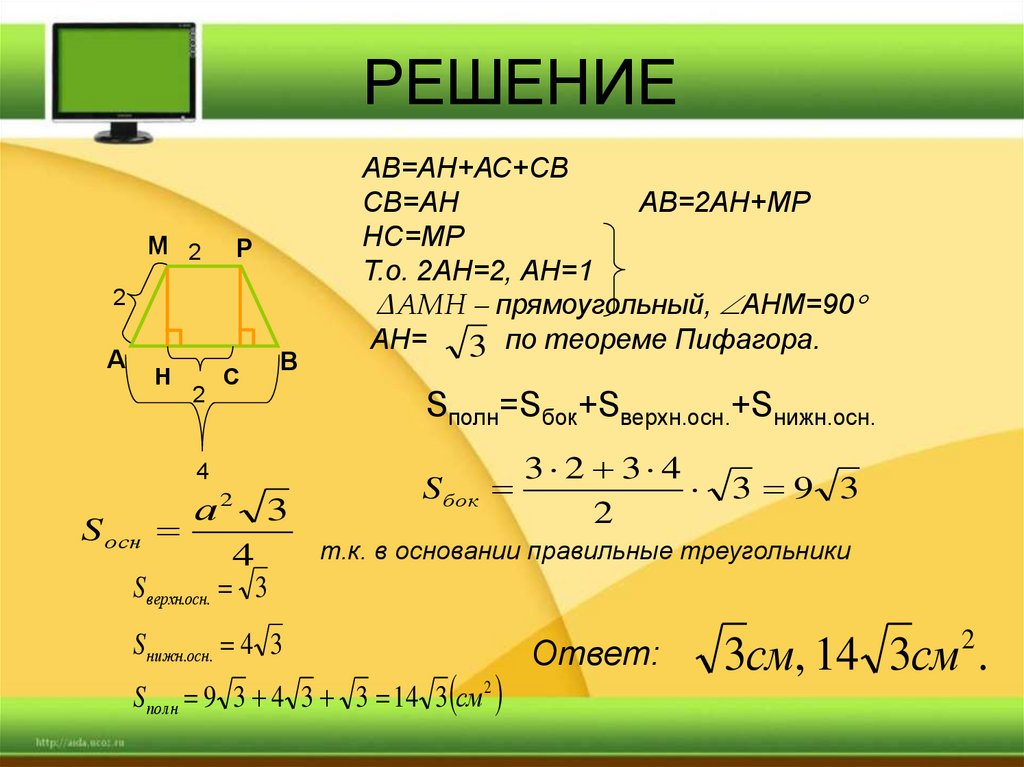
48. РЕШЕНИЕ

М 2
Р
2
А
Н
2
С
В
4
S осн
а2 3
4
АВ=АН+АС+СВ
СВ=АН
АВ=2АН+МР
НС=МР
Т.о. 2АН=2, АН=1
∆АМН – прямоугольный, АНМ=90
АН= 3 по теореме Пифагора.
Sполн=Sбок+Sверхн.осн.+Sнижн.осн.
S бок
3 2 3 4
3 9 3
2
т.к. в основании правильные треугольники
Sверхн.осн. 3
S нижн.осн. 4 3
S полн 9 3 4 3 3 14 3 см 2
Ответ:
3см, 14 3см .
2

49. ЗАДАЧА 2

Плоскость, параллельная плоскости
основания правильной четырехугольной
пирамиды, делит высоту пирамиды в
отношении 1:2, считая от вершины
пирамиды. Апофема полученной усеченной
пирамиды равна 4 см, а площадь её полной
поверхности равна 186 см2.
Найдите высоту усечённой пирамиды.