Similar presentations:
Пирамида
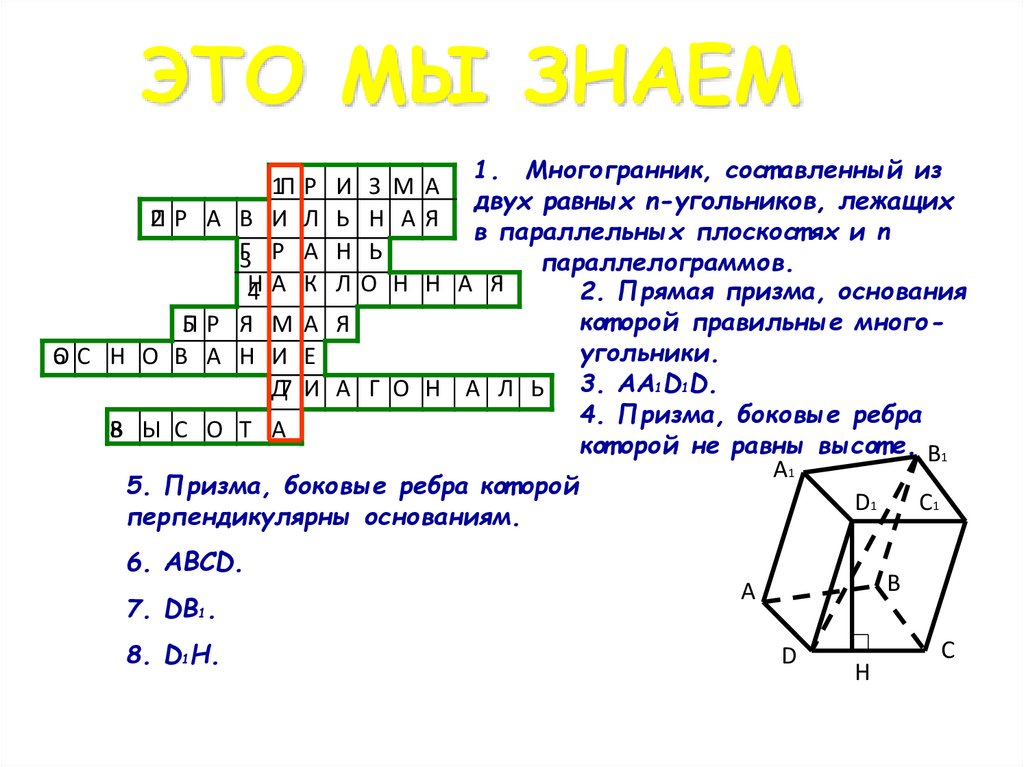
1. ЭТО МЫ ЗНАЕМ
1. Многогранник, сост авленный из1П Р И З М А
двух равных n-угольников, лежащих
2 Р А В И Л Ь Н АЯ
П
в параллельных плоскост ях и n
Г3 Р А Н Ь
параллелограммов.
Н
4 А К ЛО Н Н А Я
2. Прямая призма, основания
кот орой правильные многоугольники.
3. AA1D1D.
4. Призма, боковые ребра
В Ы С О Т А
8
кот орой не равны высот е. B1
A1
5. Призма, боковые ребра кот орой
D1
C1
перпендикулярны основаниям.
ПР Я М А Я
5
6 С Н О В А Н И Е
О
Д7 И А Г О Н А Л Ь
6. ABCD.
7. DB1.
8. D1H.
B
A
D
H
C
2.
3.
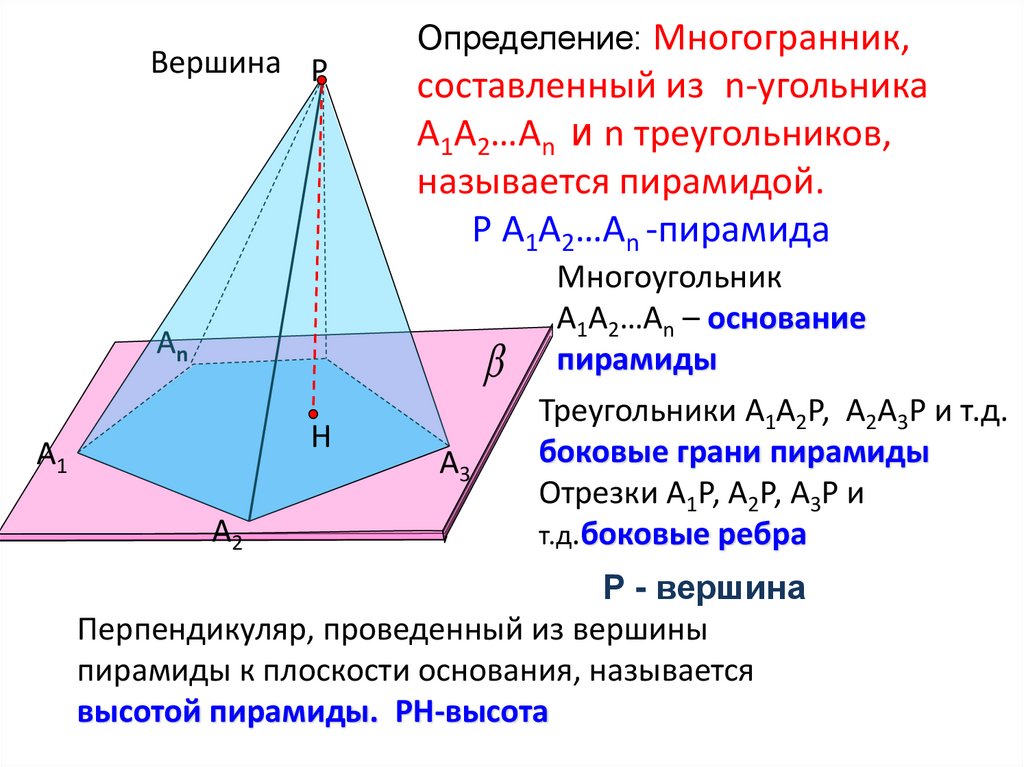
Вершина РОпределение: Многогранник,
составленный из n-угольника
А1А2…Аn и n треугольников,
называется пирамидой.
Р А1А2…Аn -пирамида
Аn
Н
А1
А2
А3
Многоугольник
А1А2…Аn – основание
пирамиды
Треугольники А1А2Р, А2А3Р и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и
т.д.боковые ребра
Р - вершина
Перпендикуляр, проведенный из вершины
пирамиды к плоскости основания, называется
высотой пирамиды. PH-высота
4.
SSН
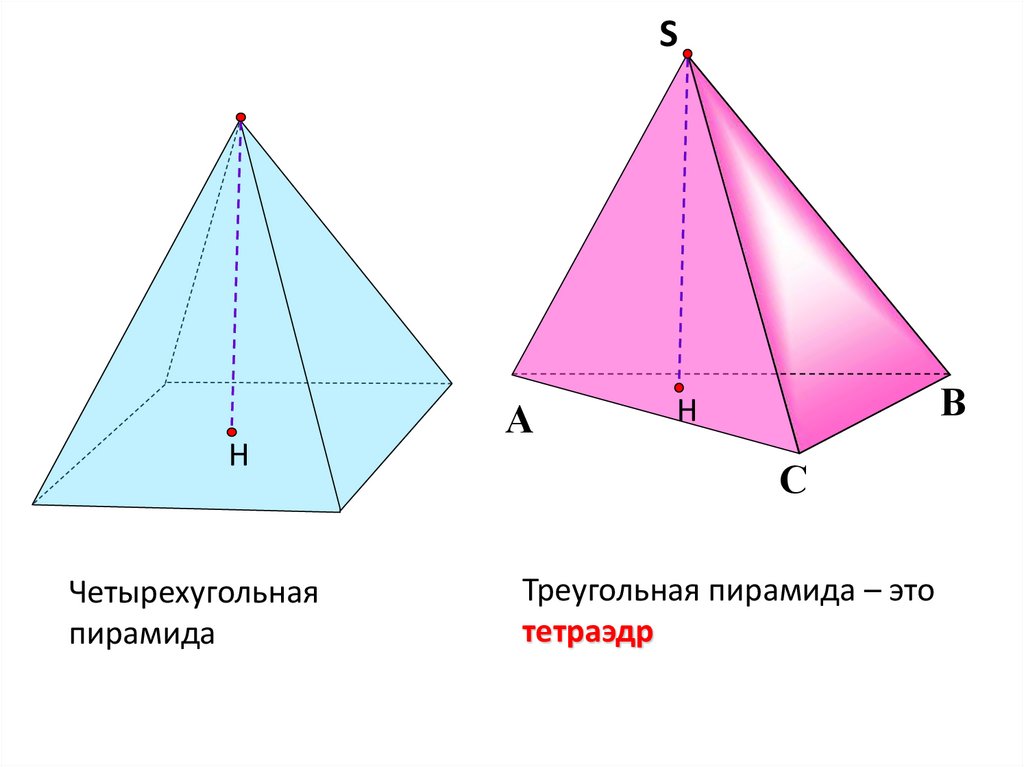
Четырехугольная
пирамида
А
В
Н
С
Треугольная пирамида – это
тетраэдр
5.
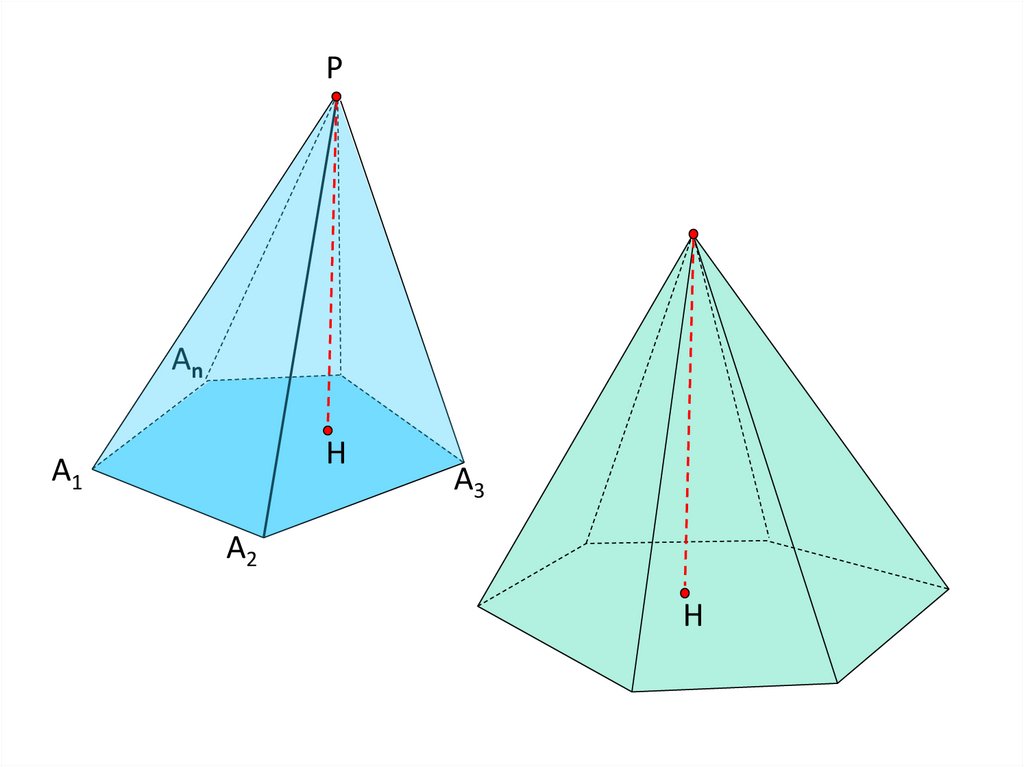
РАn
Н
А1
А3
А2
Н
6. Площадь полной поверхности пирамиды
S полн Sбок Sосн7.
Определение: Пирамида называется правильной, если ееоснование- правильный многоугольник, а отрезок,
соединяющий вершину с центром основания, является ее
высотой.
Центром правильного многоугольника
называется центр вписанной (или
описанной около него окружности).
Н
8.
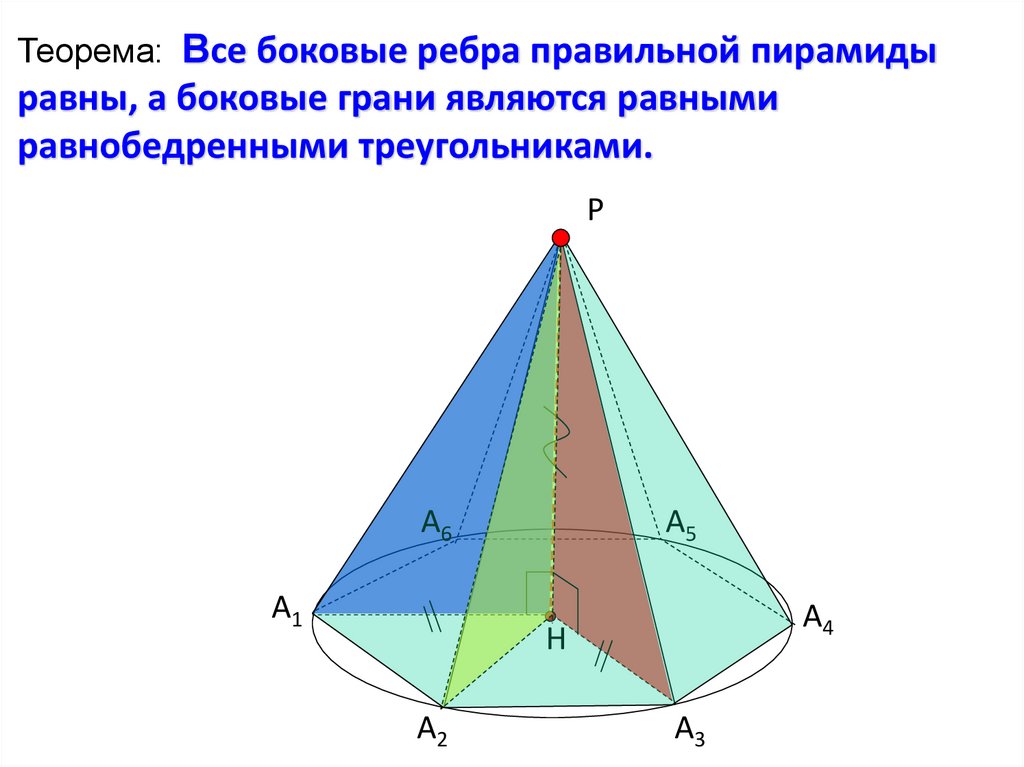
Теорема: Все боковые ребра правильной пирамидыравны, а боковые грани являются равными
равнобедренными треугольниками.
Р
А6
А1
А5
А4
Н
А2
А3
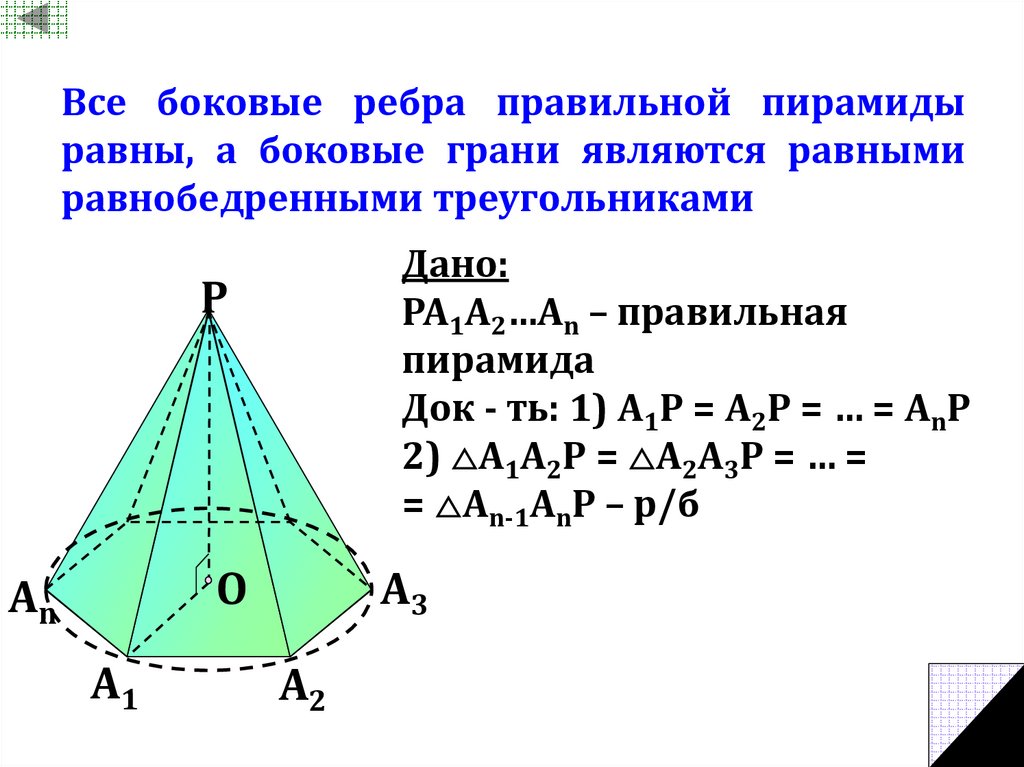
9. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками
Дано:PA1A2…An – правильная
пирамида
Док - ть: 1) А1Р = А2Р = … = АnР
2) А1А2Р = А2А3Р = … =
= Аn-1АnР – р/б
Р
О
Аn
А1
А3
А2
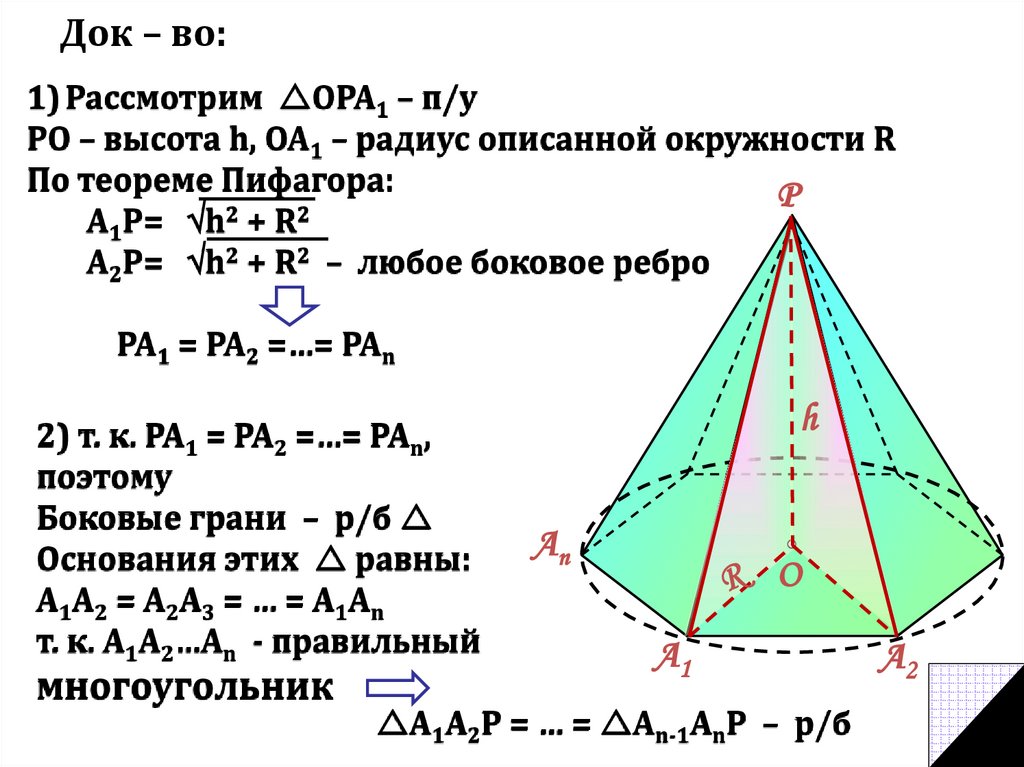
10. Док – во:
1) Рассмотрим ОРА1 – п/уРО – высота h, OA1 – радиус описанной окружности R
По теореме Пифагора:
Р
2
2
A1P= h + R
A2P= h2 + R2 – любое боковое ребро
РА1 = РА2 =…= РАn
2) т. к. РА1 = РА2 =…= РАn,
поэтому
Боковые грани – р/б
Основания этих равны:
А1А2 = А2А3 = … = А1Аn
т. к. А1А2…Аn - правильный
многоугольник
h
Аn
О
А1
А1А2Р = … = Аn-1АnР – р/б
А2
11.
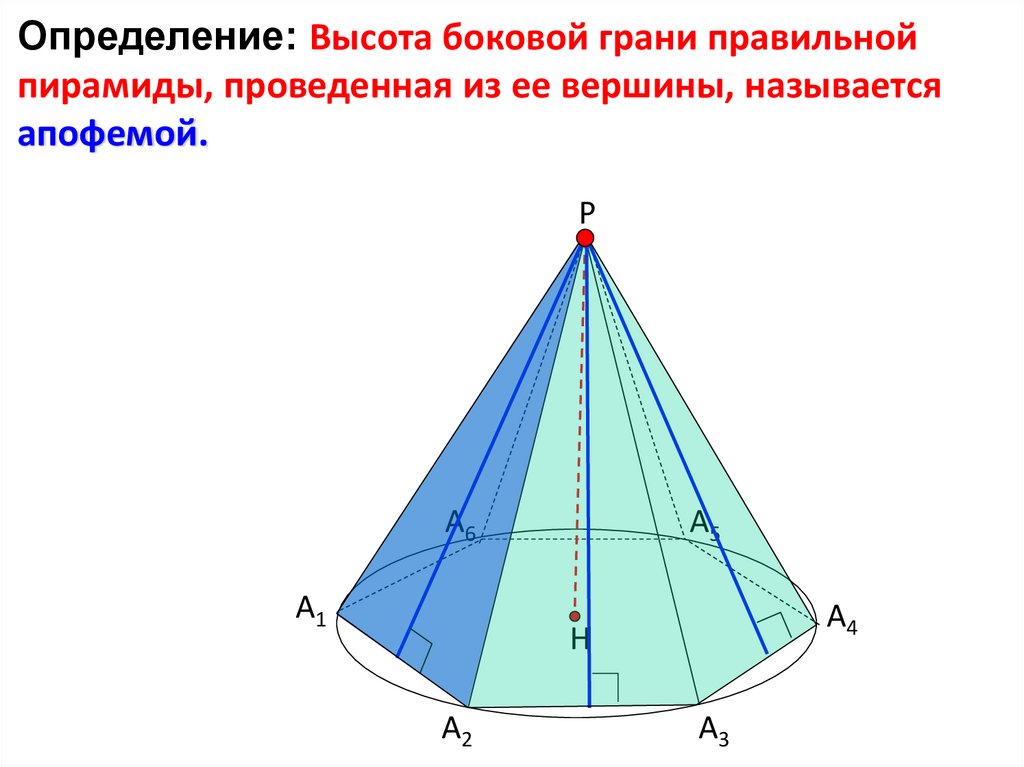
Определение: Высота боковой грани правильнойпирамиды, проведенная из ее вершины, называется
апофемой.
Р
А6
А1
А5
А4
Н
А2
А3
12.
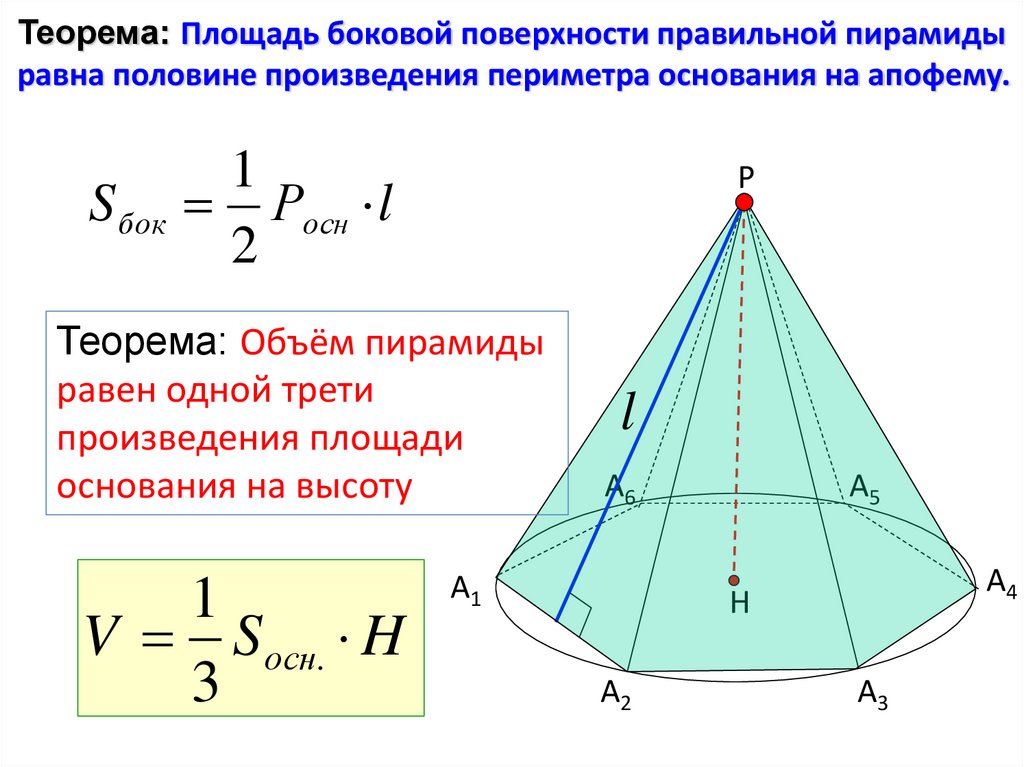
Теорема: Площадь боковой поверхности правильной пирамидыравна половине произведения периметра основания на апофему.
1
S бок Росн l
2
Р
Теорема: Объём пирамиды
равен одной трети
произведения площади
основания на высоту
1
V S осн. H
3
l
А6
А1
А5
А4
Н
А2
А3
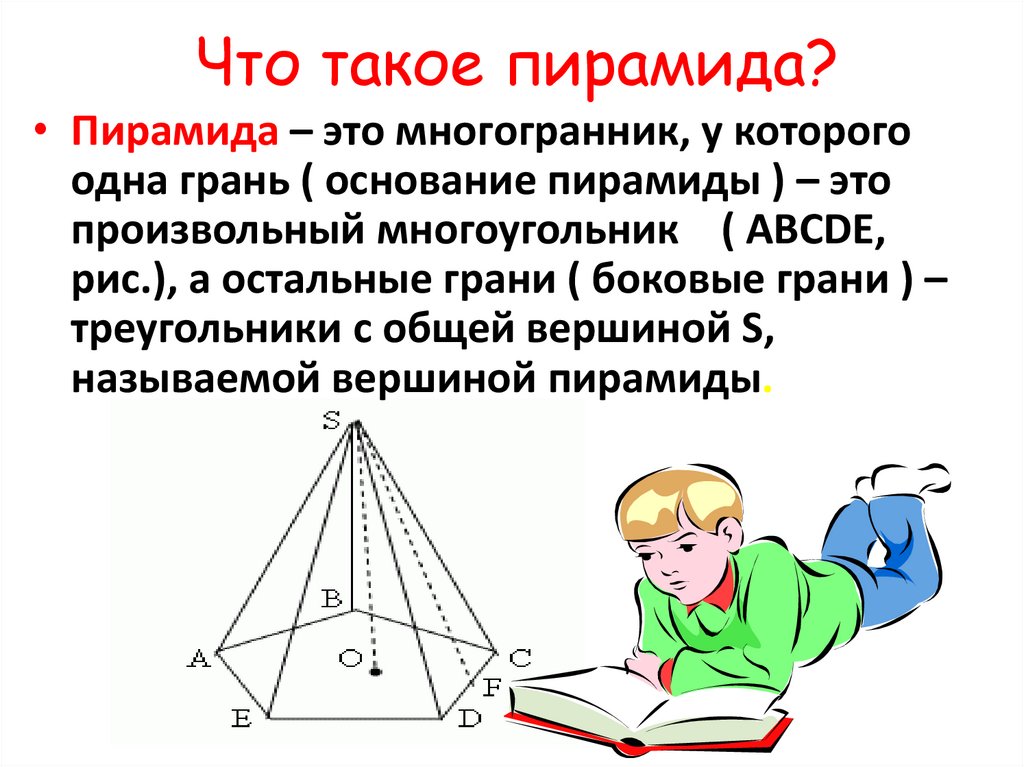
13. Что такое пирамида?
• Пирамида – это многогранник, у которогоодна грань ( основание пирамиды ) – это
произвольный многоугольник ( ABCDE,
рис.), а остальные грани ( боковые грани ) –
треугольники с общей вершиной S,
называемой вершиной пирамиды.
14.
ПРОВЕРЬ СЕБЯОснование - многоугольник.
ABC
Боковые грани - треугольники.
ABP, BCP, ACP
Вершина - общая. точка всех
P
боковых граней.
Боковые ребра - отрезки,
соединяющие вершину с
вершинами основания.
AP, BP, CP
Высот а - перпендикуляр,
A
проведенный из вершины к
плоскости основания. PH
P
B
H
C
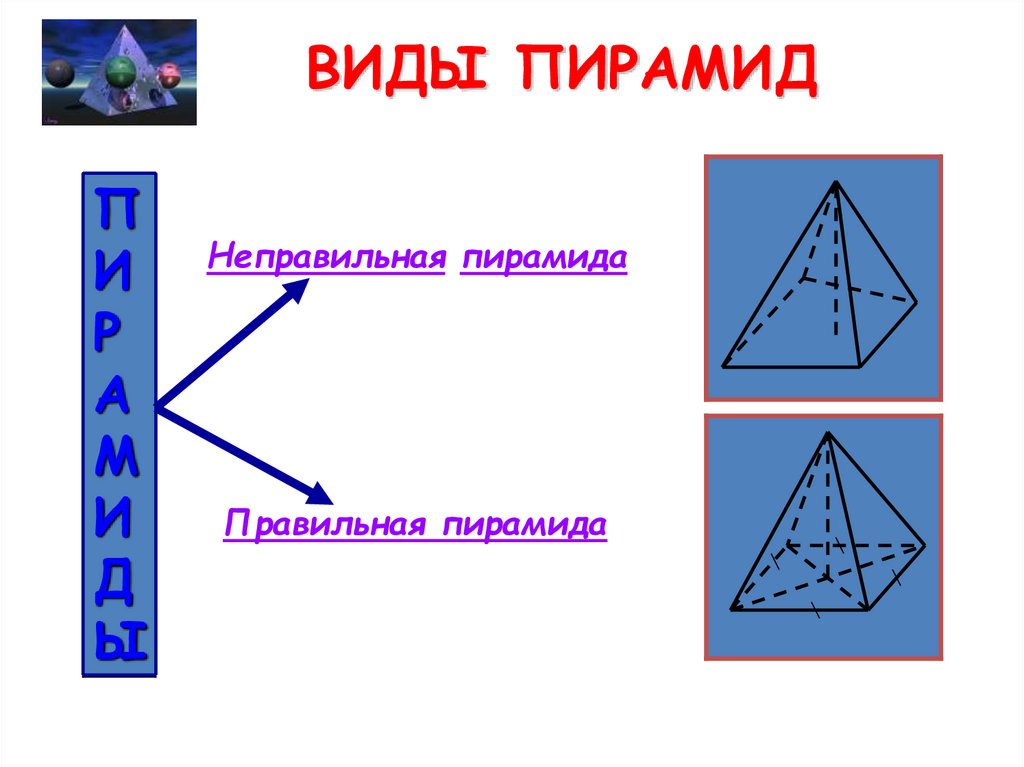
15. ВИДЫ ПИРАМИД
ПИ
Р
А
М
И
Д
Ы
Неправильная пирамида
Правильная пирамида
16.
ПРАВИЛЬНАЯ ПИРАМИДАПирамида называется правильной, если в основании
лежит правильный многоугольник, а отрезок,
соединяющий вершину пирамиды с центром её
основания, является высотой пирамиды.
•Боковые ребра равны
P
•Боковые грани – равные
равнобедренные треугольники
B
C B
C B
P
C B
Апофема правильной
пирамиды
H
H –
Aвысота ее
D боковой
A
D
A
D
A
грани,
проведенная
из вершины.
PK - апофема
C
K
H
D
17. ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПРАВИЛЬНОЙ ПИРАМИДЫ
Sбок. = 1/2Pосн. * lгде
Pосн. – периметр основания,
l –апофема правильной пирамиды.
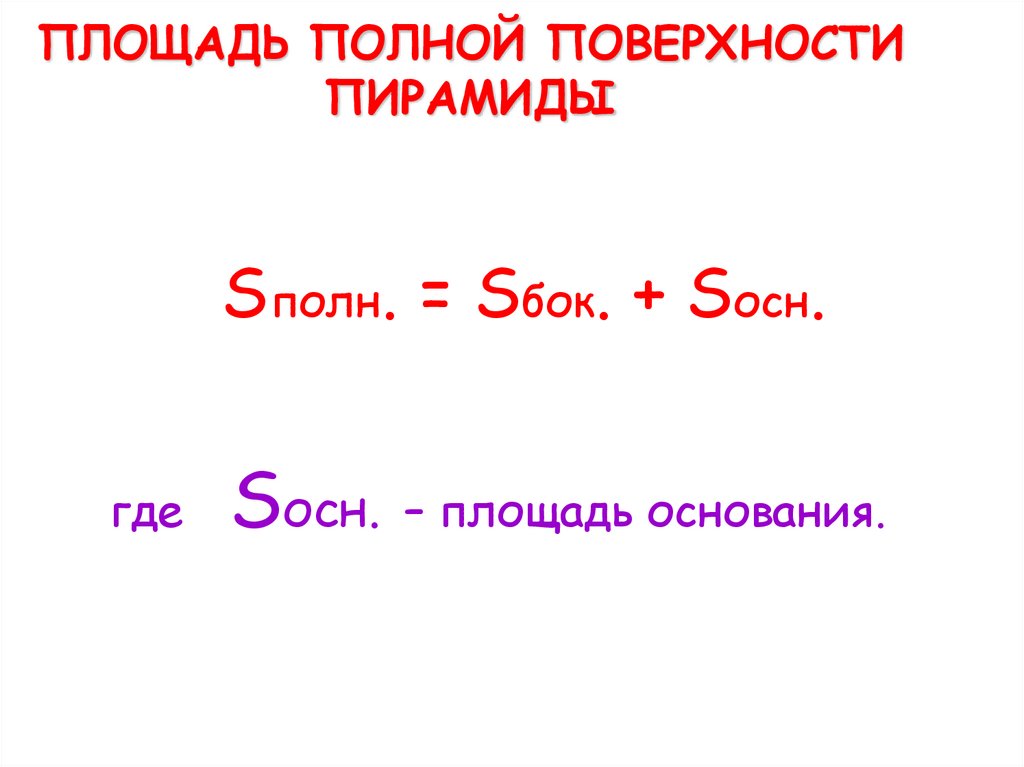
18. ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ПИРАМИДЫ
Sполн. = Sбок. + Sосн.где
Sосн. – площадь основания.
19. ОБЪЁМ ПИРАМИДЫ
1V = Sосн. * h
3
где
Sосн. – площадь основания,
h – высота пирамиды.
20. Заполни таблицу
Наклоннаяпризма
Sбок
Площадь
боковой
поверхности
Sполн
Площадь
полной
поверхности
V
Объем
Прямая призма
Прямоугольный
параллелепипед
Куб
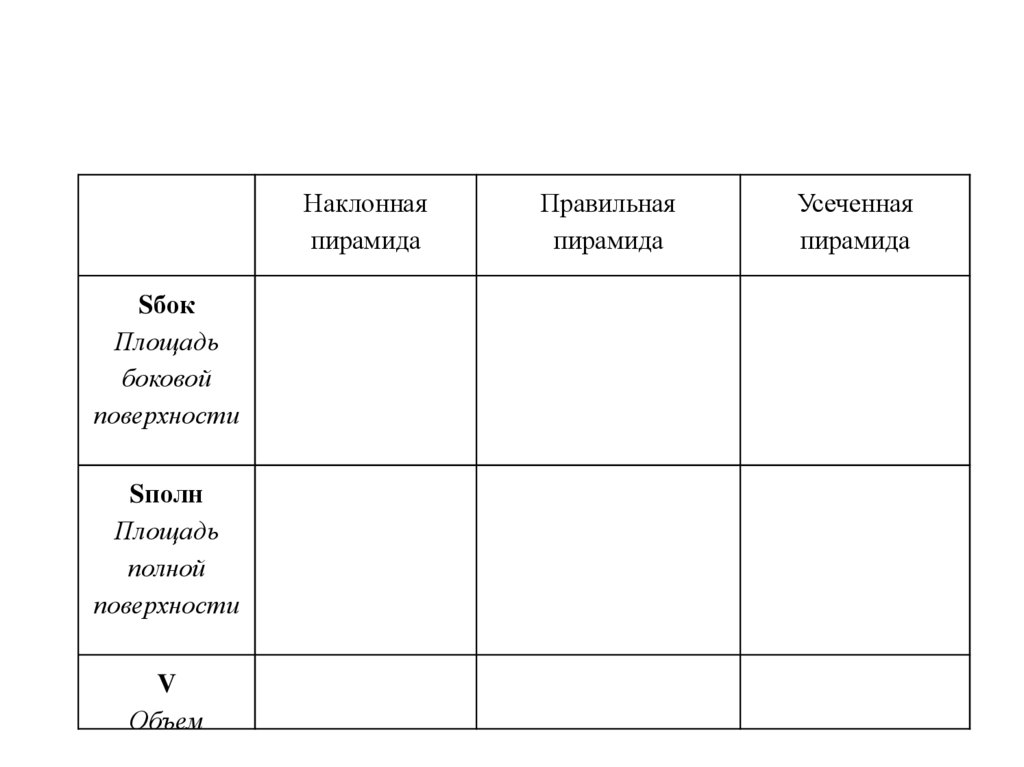
21.
Наклоннаяпирамида
Sбок
Площадь
боковой
поверхности
Sполн
Площадь
полной
поверхности
V
Объем
Правильная
пирамида
Усеченная
пирамида
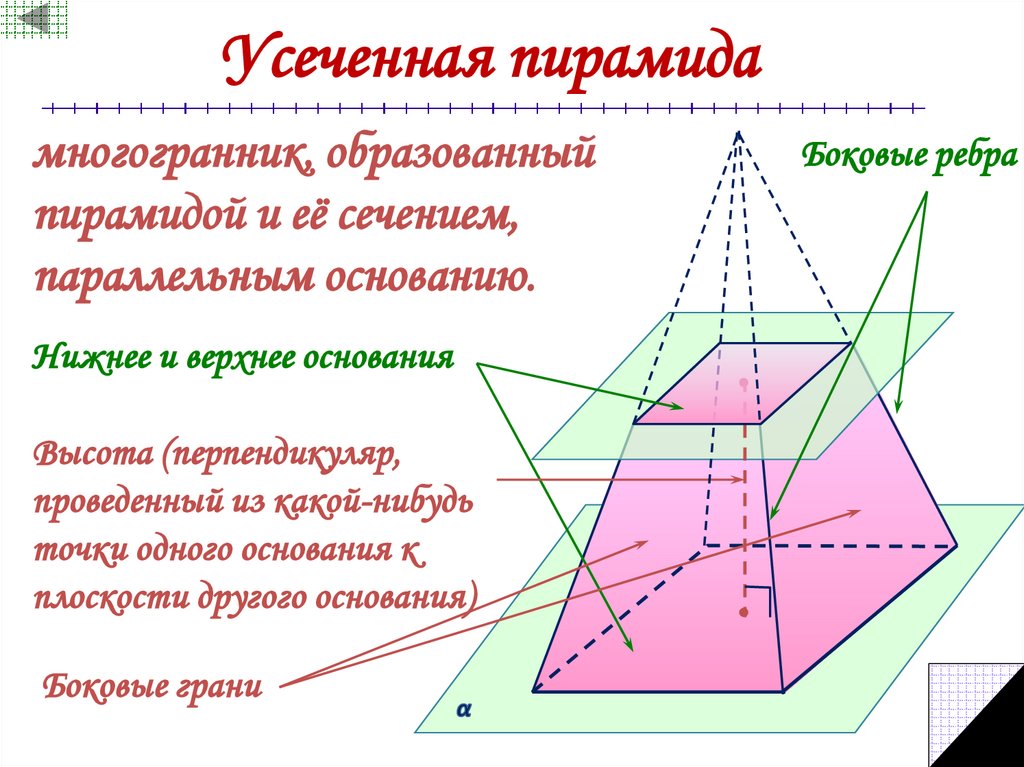
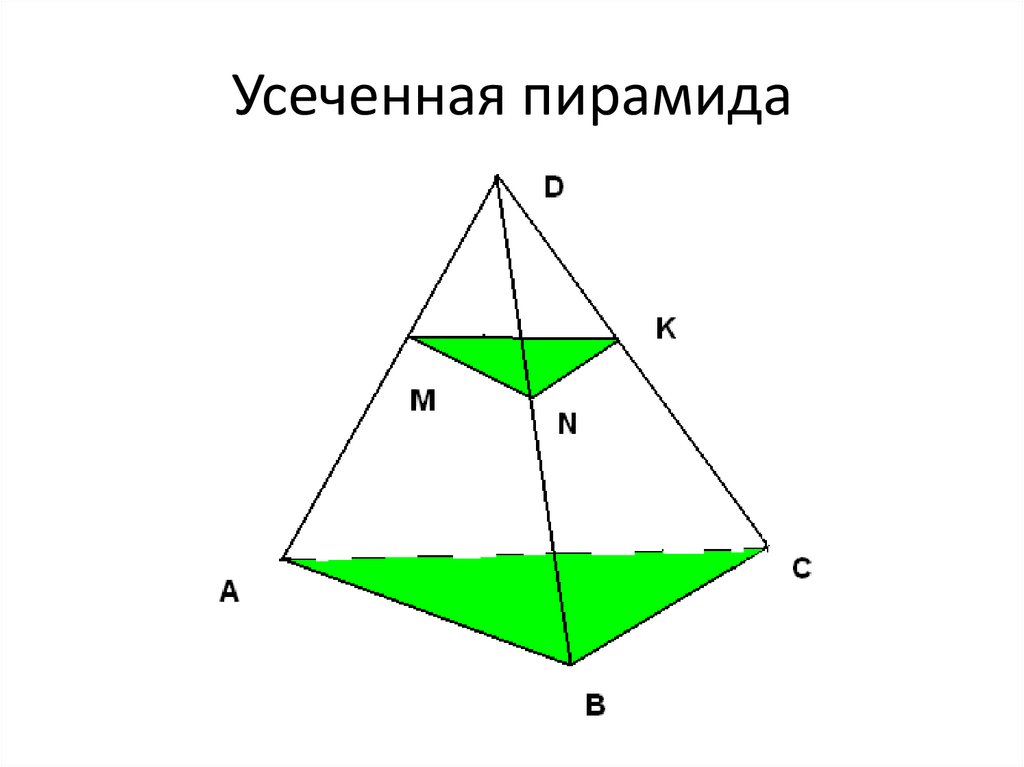
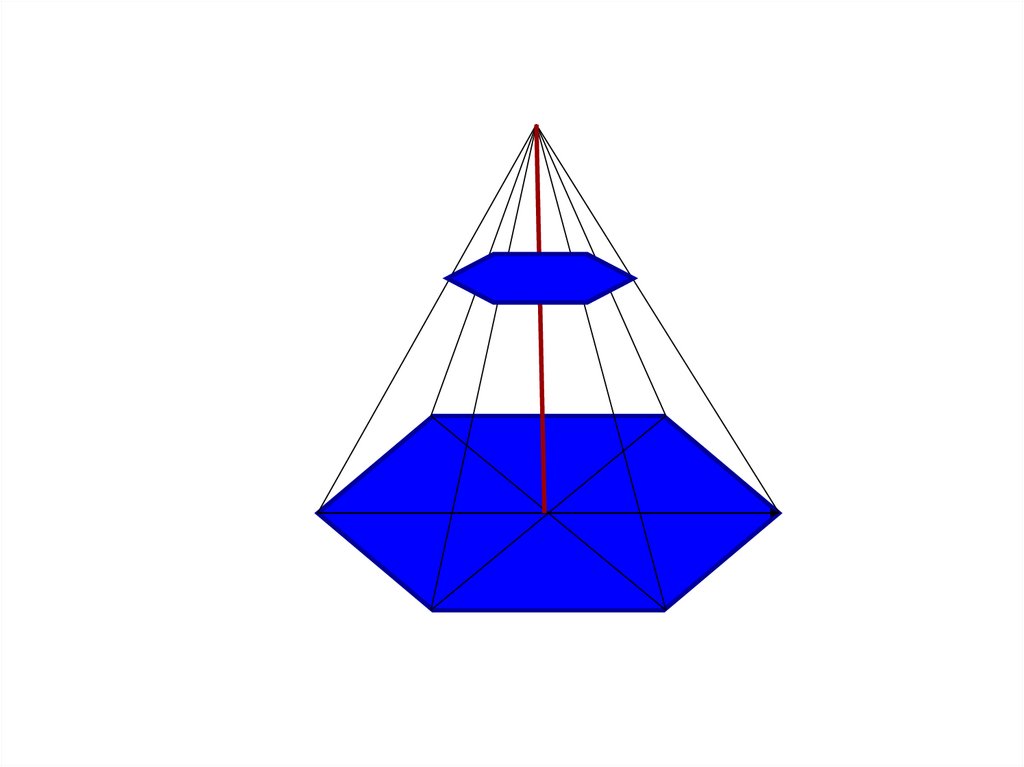
22. Усеченная пирамида
23. Усеченная пирамида
многогранник, образованныйпирамидой и её сечением,
параллельным основанию.
Нижнее и верхнее основания
Высота (перпендикуляр,
проведенный из какой-нибудь
точки одного основания к
плоскости другого основания)
Боковые грани
Боковые ребра
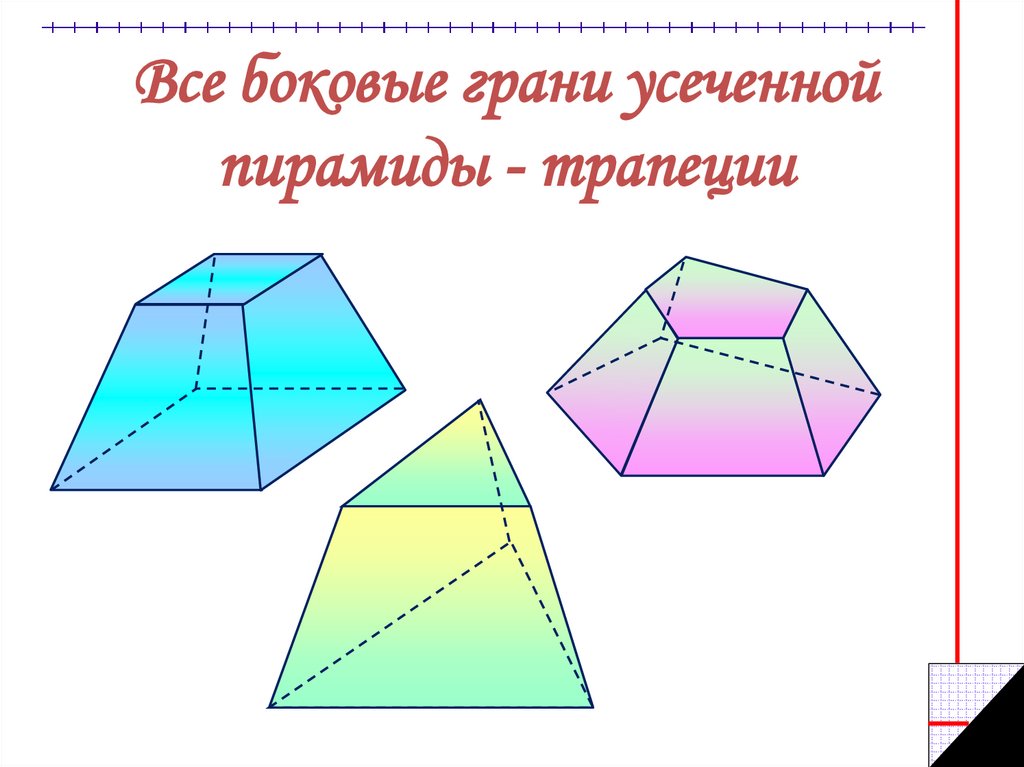
24. Все боковые грани усеченной пирамиды - трапеции
25.
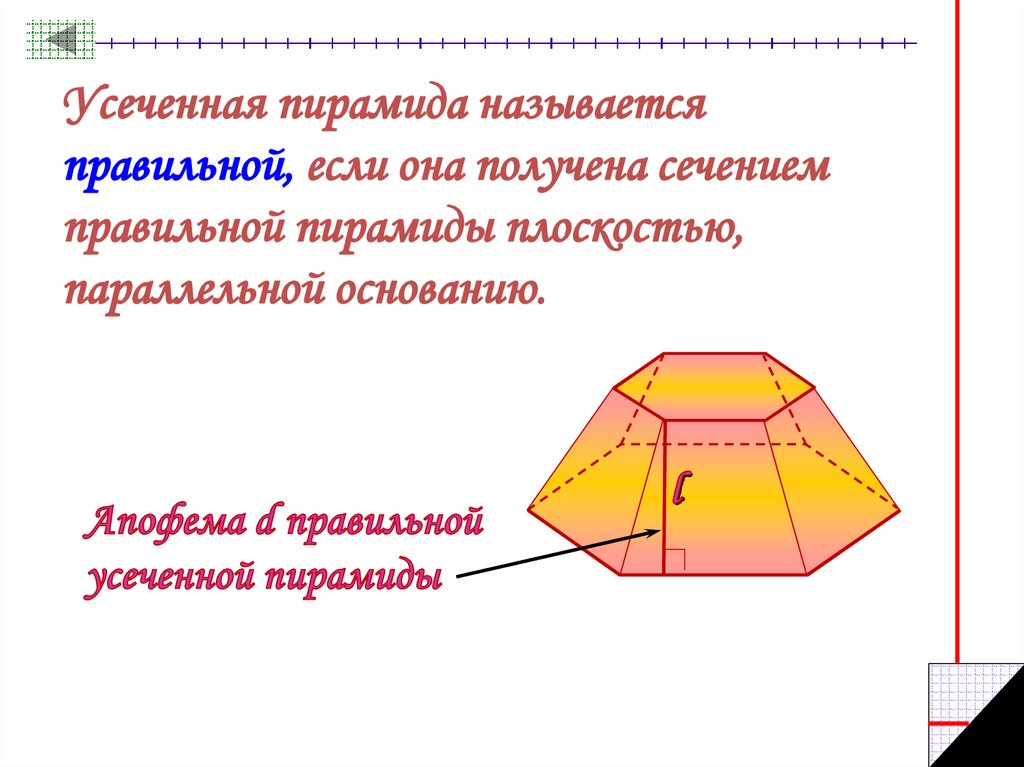
Усеченная пирамида называетсяправильной, если она получена сечением
правильной пирамиды плоскостью,
параллельной основанию.
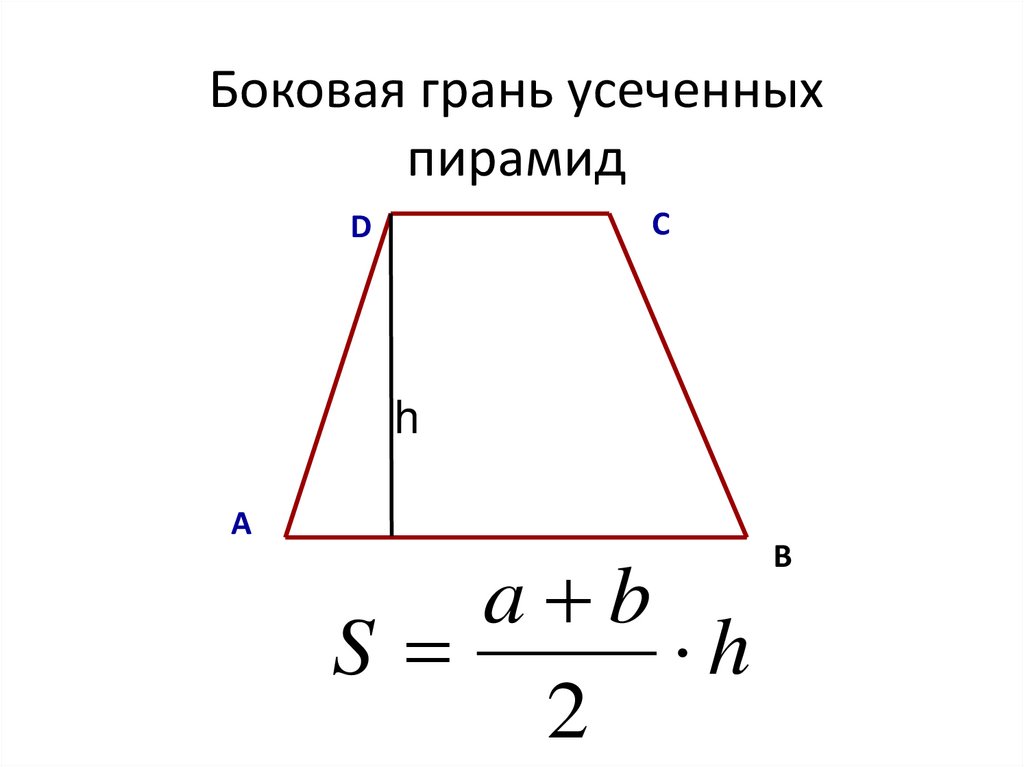
26. Боковая грань усеченных пирамид
СD
h
А
a b
S
h
2
В
27. Теорема о площади боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильнойусеченной пирамиды равна произведению
полусуммы периметров оснований на апофему
a2
S бок = ½(Р1 + Р2) l
Док – во:
S бок = ½l(a1+a2) + ½l(a1+a2) +
+ ½ l(a1+a2) + ½l(a1+a2) =
= ½l(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) =
= ½l(4a1+ 4a2) = ½l(P1+ P2)
P2= 4a2
l
a1
P1= 4a1
28. Площадь полной поверхности усеченной пирамиды
S полн Sбок Sосн1 Sосн 2Объём V усечённой пирамиды, высота которой
равна H, а площади оснований равны S и S1,
вычисляется по формуле:
1
V H ( S1 S 2 S1 S 2 )
3
29. Усеченная пирамида
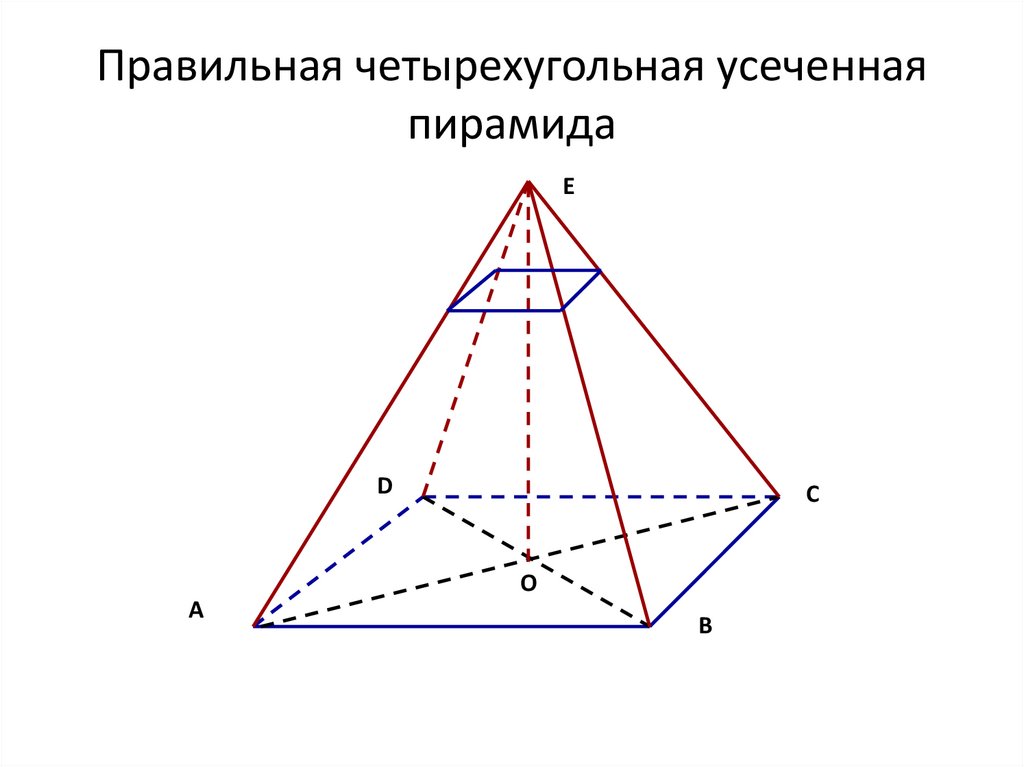
30. Правильная четырехугольная усеченная пирамида
ЕD
С
О
А
В

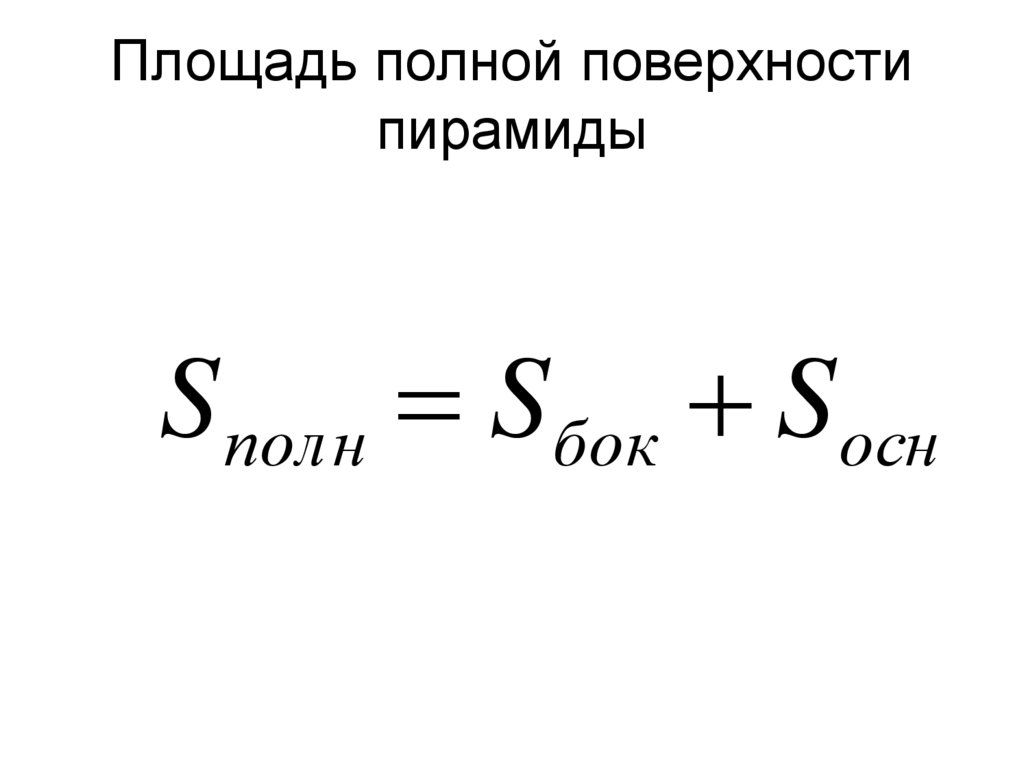









 mathematics
mathematics








