Similar presentations:
Комплексный чертеж плоскости
1.
2.
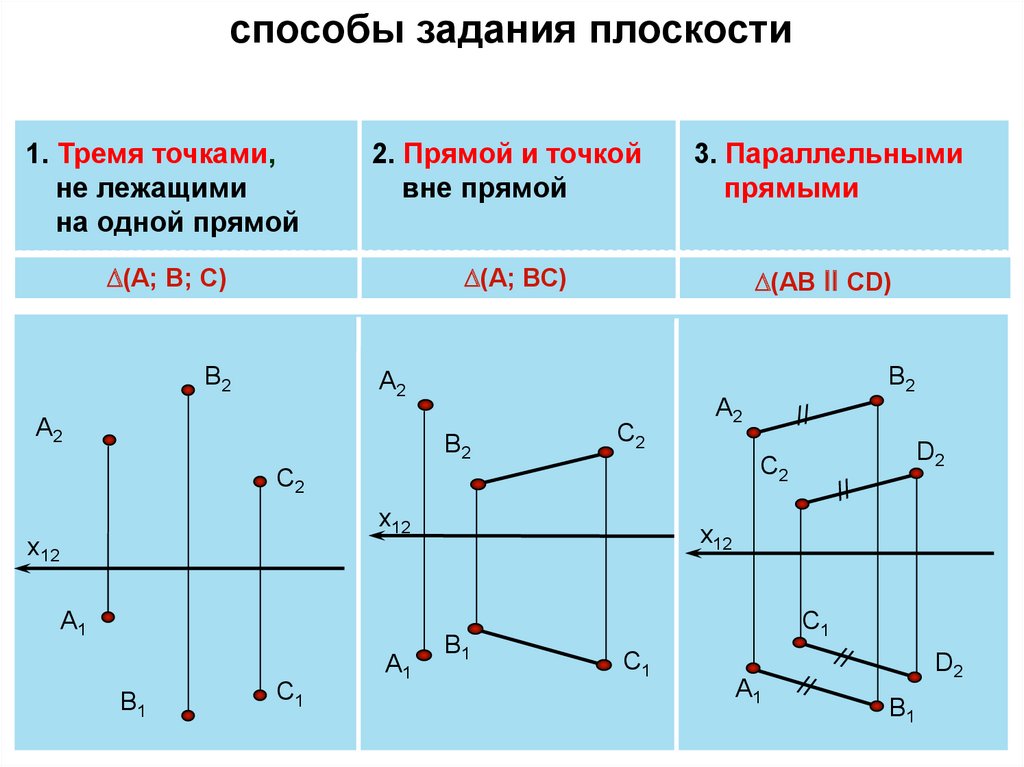
способы задания плоскости1. Тремя точками,
не лежащими
на одной прямой
2. Прямой и точкой
вне прямой
3. Параллельными
прямыми
(А; ВС)
(А; В; С)
В2
(АВ ll СD)
А2
А2
В2
С2
А2
х12
А1
В1
С1
А1
D2
С2
С2
х12
В2
х12
В1
С1
С1
А1
D2
В1
3.
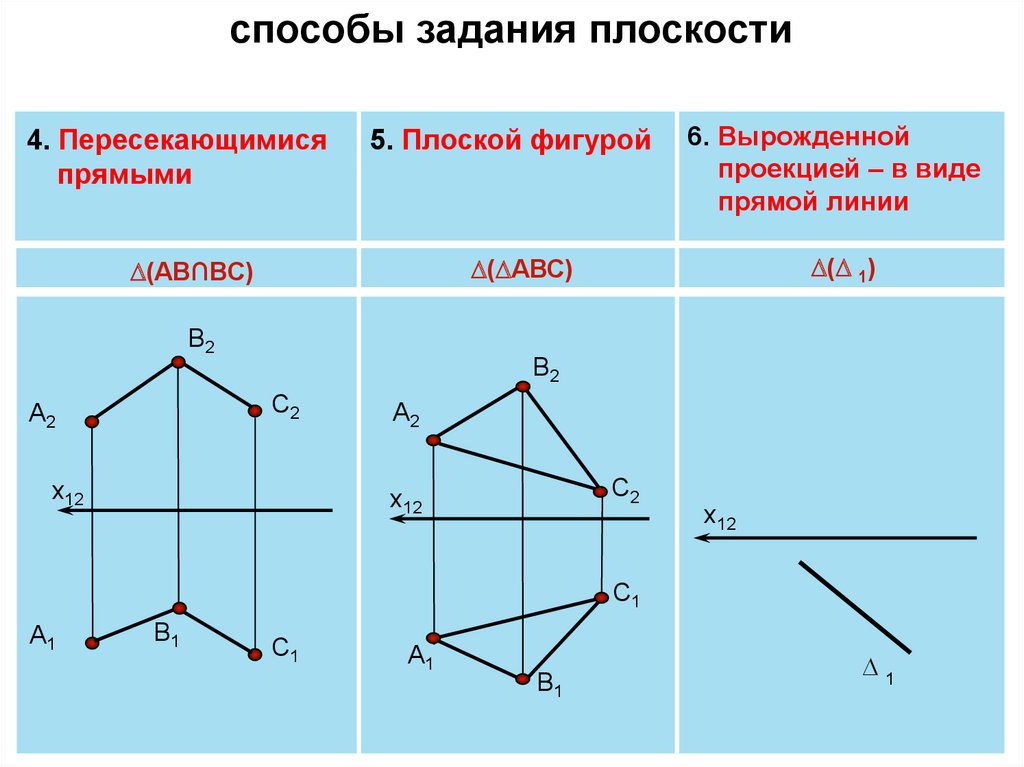
способы задания плоскости4. Пересекающимися
прямыми
5. Плоской фигурой
( 1)
( АВС)
(АВ∩ВС)
В2
В2
С2
А2
6. Вырожденной
проекцией – в виде
прямой линии
х12
А2
С2
х12
х12
С1
А1
В1
С1
А1
В1
1
4.
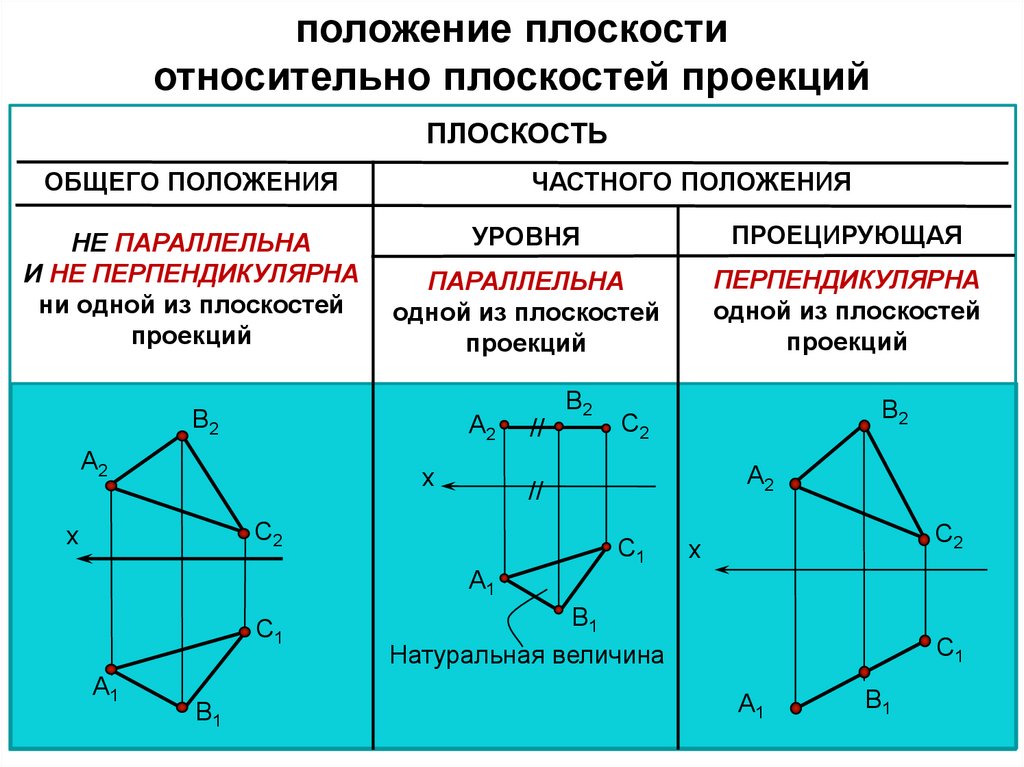
положение плоскостиотносительно плоскостей проекций
ПЛОСКОСТЬ
ОБЩЕГО ПОЛОЖЕНИЯ
НЕ ПАРАЛЛЕЛЬНА
И НЕ ПЕРПЕНДИКУЛЯРНА
ни одной из плоскостей
проекций
ЧАСТНОГО ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩАЯ
ПАРАЛЛЕЛЬНА
одной из плоскостей
проекций
ПЕРПЕНДИКУЛЯРНА
одной из плоскостей
проекций
В2
А2
А2
х
А1
С1
А1
В1
В2
С2
А2
//
С2
х
//
В2
С1
С2
х
В1
Натуральная величина
С1
А1
В1
5.
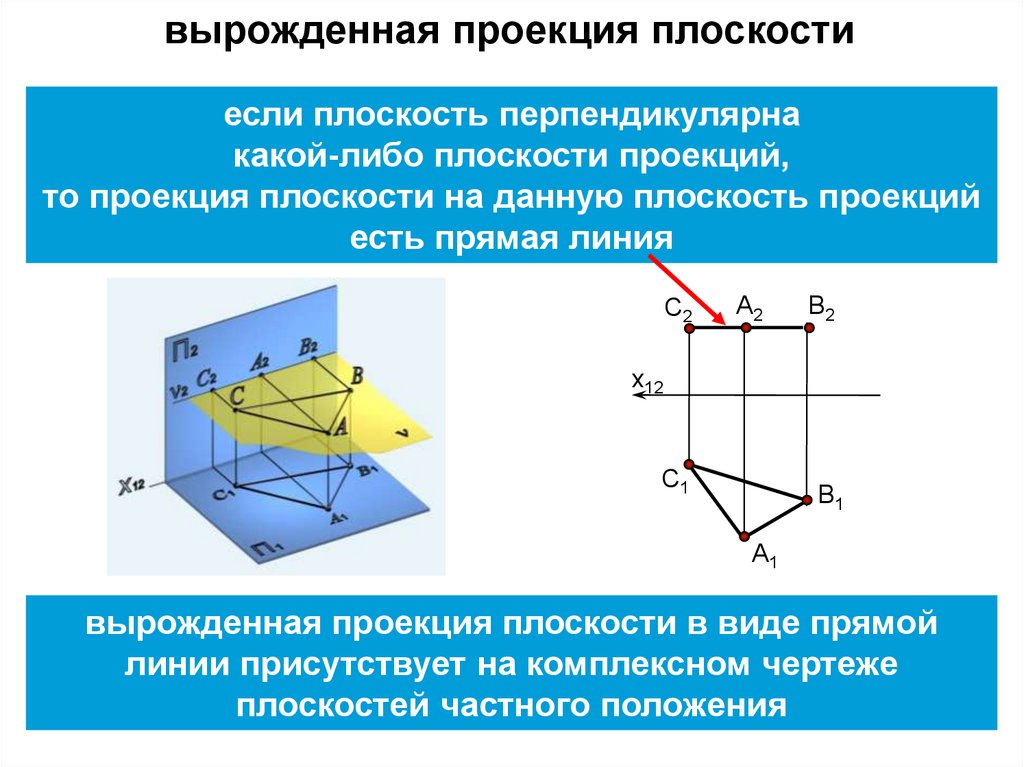
вырожденная проекция плоскостиесли плоскость перпендикулярна
какой-либо плоскости проекций,
то проекция плоскости на данную плоскость проекций
есть прямая линия
С2
А2
В2
х12
С1
В1
А1
вырожденная проекция плоскости в виде прямой
линии присутствует на комплексном чертеже
плоскостей частного положения
6.
вырожденная проекция плоскостиобладает собирательным свойством:
любая точка принадлежащая плоскости,
проецируется на эту проекцию (прямую)
С2
А2
В2
х12
С1
В1
А1
Ѵ( ABC) П1
[ C2B2 ] – вырожденная проекция Ѵ( ABC)
7.
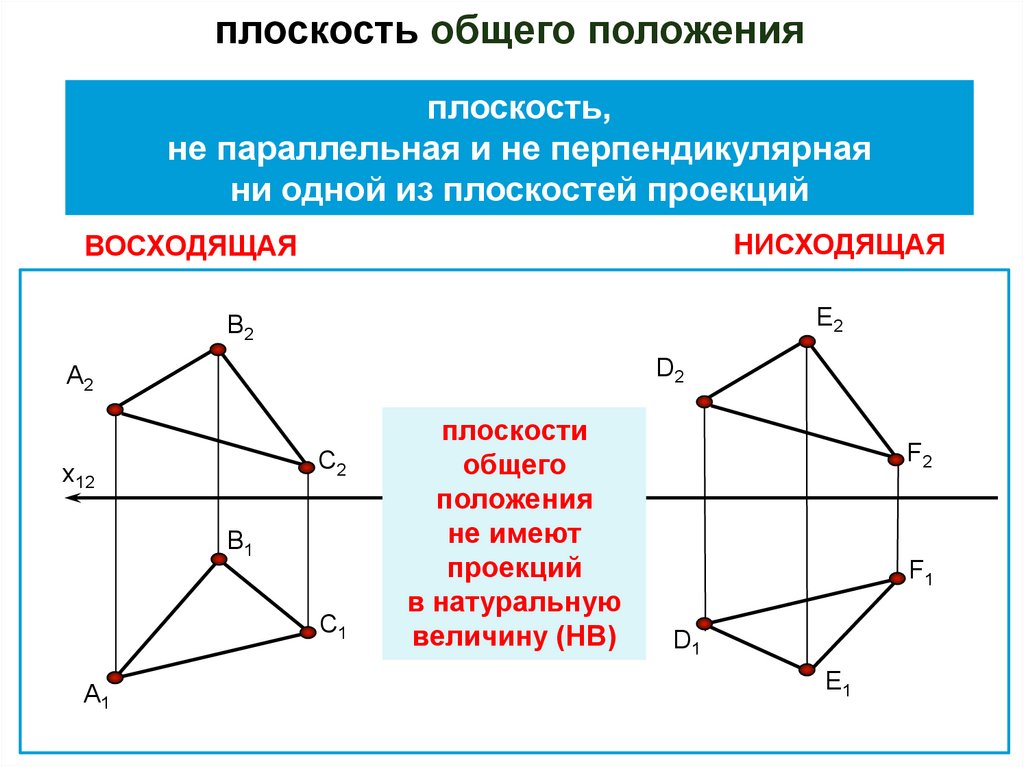
плоскость общего положенияплоскость,
не параллельная и не перпендикулярная
ни одной из плоскостей проекций
НИСХОДЯЩАЯ
ВОСХОДЯЩАЯ
E2
В2
D2
А2
С2
х12
В1
С1
А1
плоскости
общего
положения
не имеют
проекций
в натуральную
величину (НВ)
F2
F1
D1
E1
8.
ПЛОСКОСТИЧАСТНОГО ПОЛОЖЕНИЯ
9.
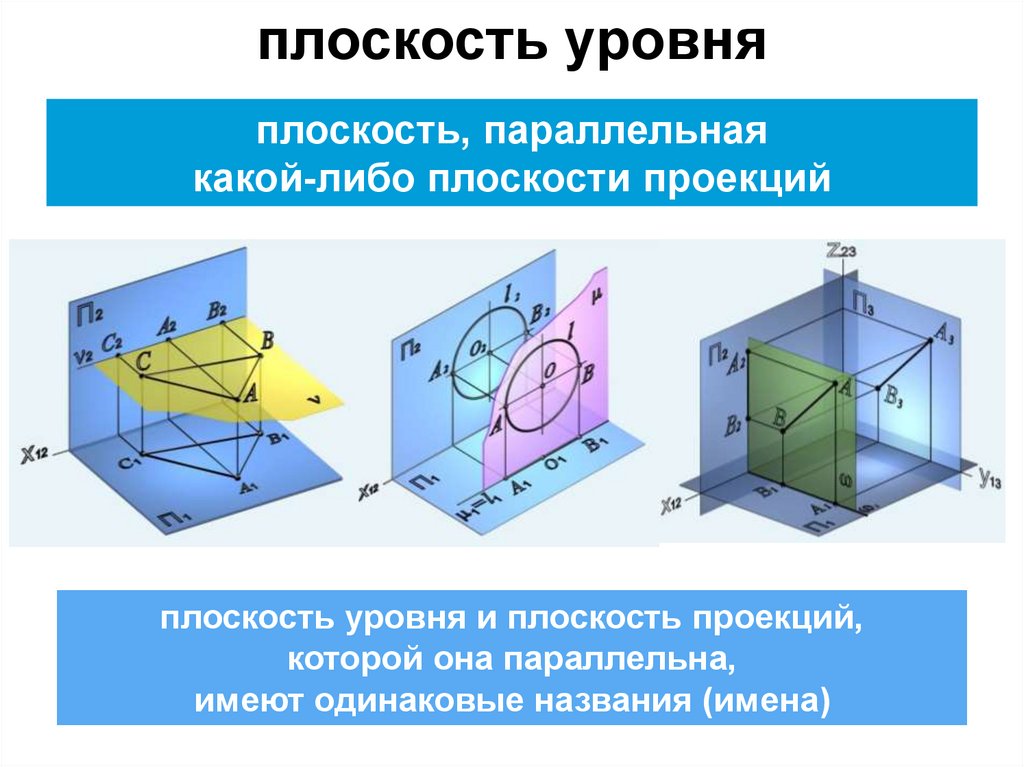
плоскость уровняплоскость, параллельная
какой-либо плоскости проекций
плоскость уровня и плоскость проекций,
которой она параллельна,
имеют одинаковые названия (имена)
10.
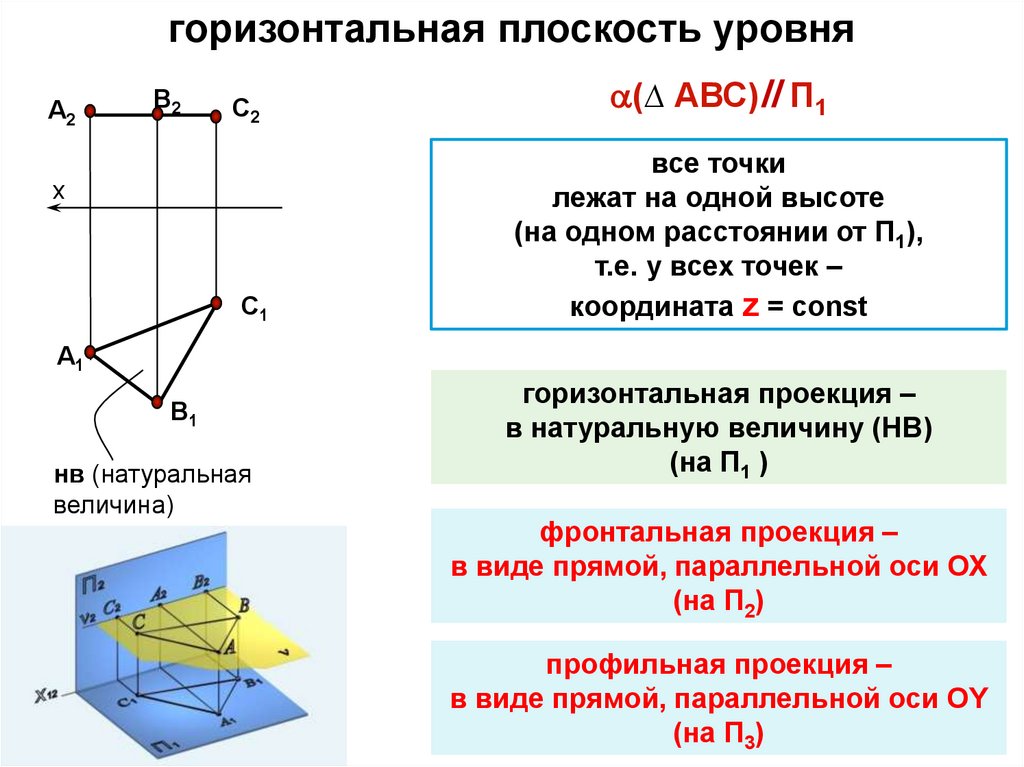
горизонтальная плоскость уровняА2
В2
С2
х
С1
(∆ АВС)ll П1
все точки
лежат на одной высоте
(на одном расстоянии от П1),
т.е. у всех точек –
координата z = const
А1
В1
нв (натуральная
величина)
горизонтальная проекция –
в натуральную величину (НВ)
(на П1 )
фронтальная проекция –
в виде прямой, параллельной оси ОХ
(на П2)
профильная проекция –
в виде прямой, параллельной оси ОY
(на П3)
11.
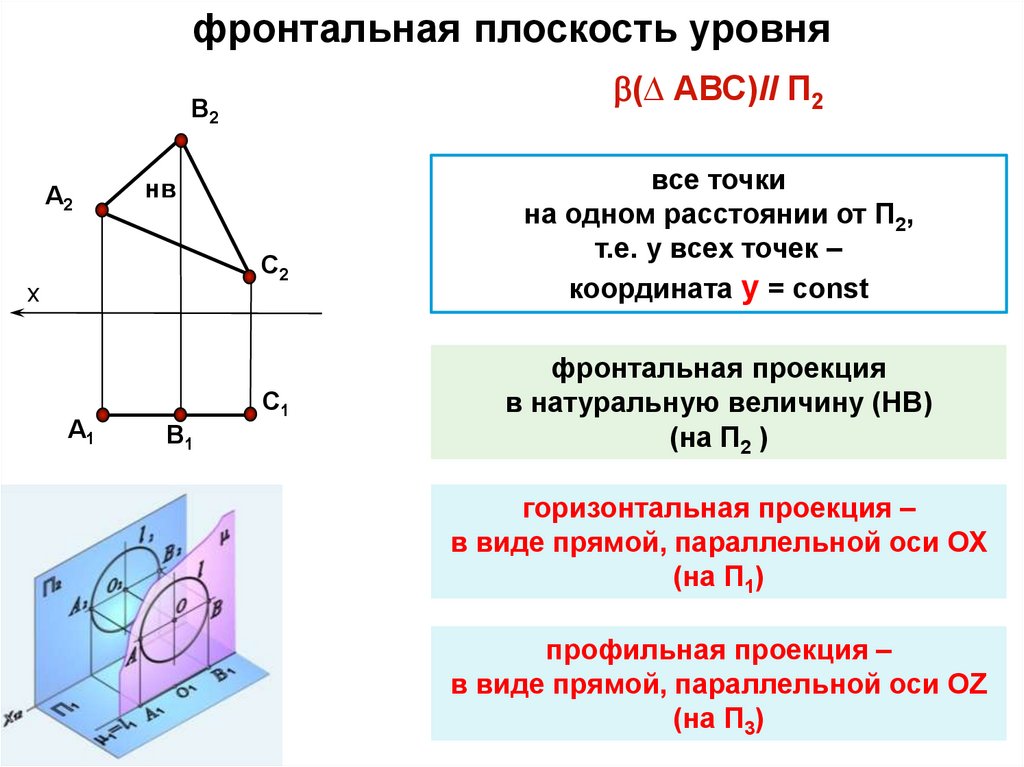
фронтальная плоскость уровня(∆ АВС)ll П2
В2
А2
нв
С2
х
А1
С1
В1
все точки
на одном расстоянии от П2,
т.е. у всех точек –
координата y = const
фронтальная проекция
в натуральную величину (НВ)
(на П2 )
горизонтальная проекция –
в виде прямой, параллельной оси ОХ
(на П1)
профильная проекция –
в виде прямой, параллельной оси ОZ
(на П3)
12.
профильная плоскость уровняz
В2
А2
А3
(∆ АВС) ll П3
В3
нв
С3
С2
А1
все точки
на одном расстоянии от П3,
т.е. у всех точек –
координата х = const
В1
С1
y
профильная проекция
в натуральную величину (НВ)
(на П3)
горизонтальная проекция –
в виде прямой, параллельной оси ОY
(на П1)
фронтальная проекция –
в виде прямой, параллельной оси ОZ
(на П2)
13.
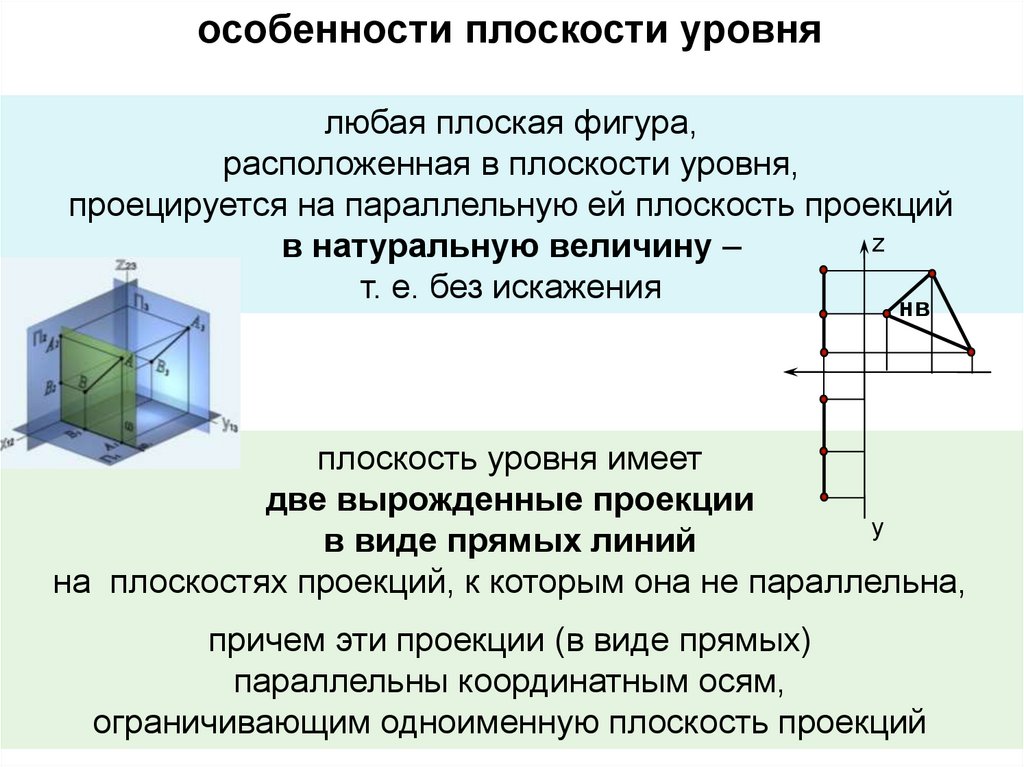
особенности плоскости уровнялюбая плоская фигура,
расположенная в плоскости уровня,
проецируется на параллельную ей плоскость проекций
z
в натуральную величину –
т. е. без искажения
нв
плоскость уровня имеет
две вырожденные проекции
y
в виде прямых линий
на плоскостях проекций, к которым она не параллельна,
причем эти проекции (в виде прямых)
параллельны координатным осям,
ограничивающим одноименную плоскость проекций
14.
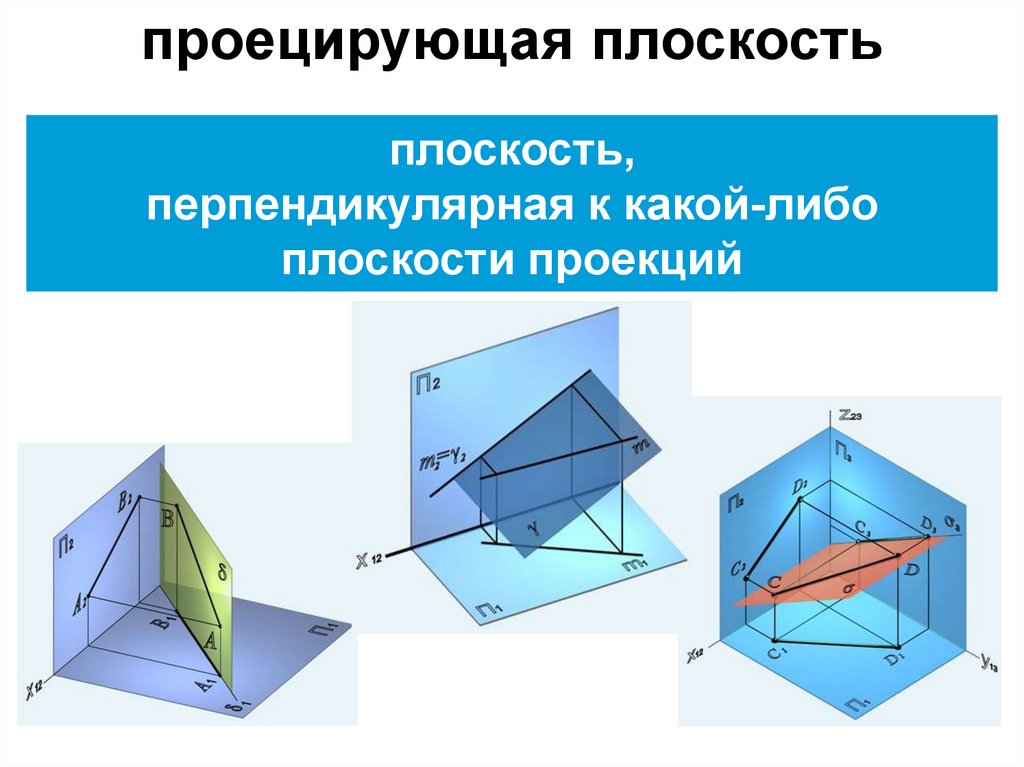
проецирующая плоскостьплоскость,
перпендикулярная к какой-либо
плоскости проекций
15.
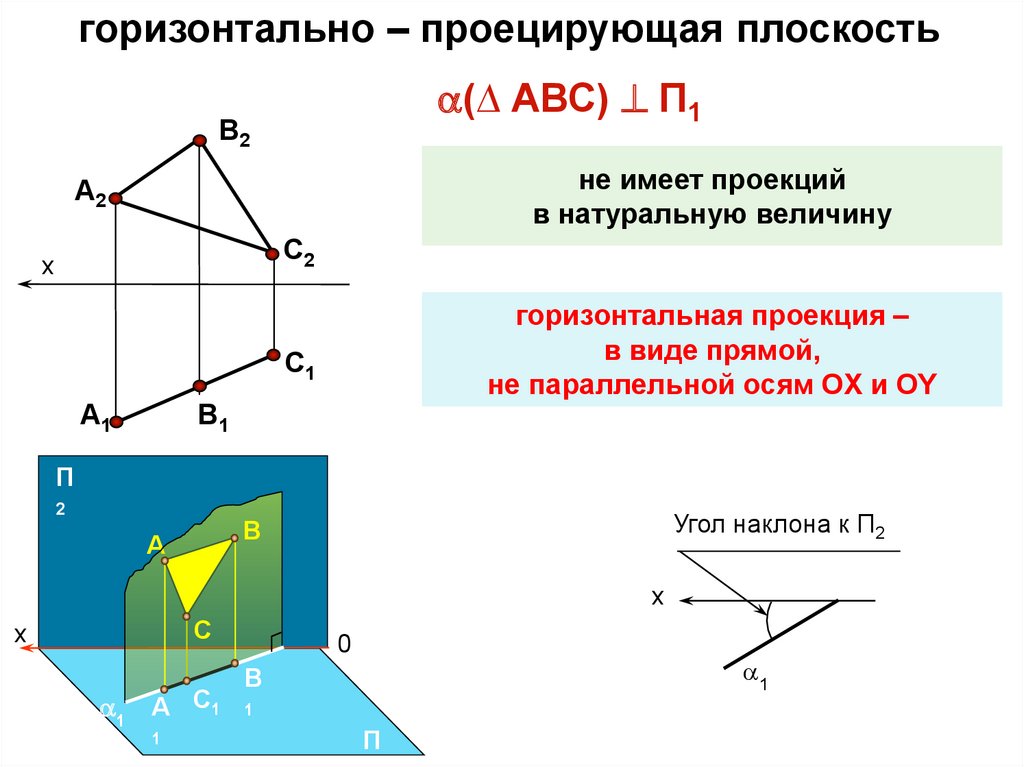
горизонтально – проецирующая плоскость(∆ АВС) П1
В2
не имеет проекций
в натуральную величину
А2
С2
х
горизонтальная проекция –
в виде прямой,
не параллельной осям OX и ОY
С1
А1
В1
П
2
Угол наклона к П2
B
A
x
C
x
1
A С1
1
0
1
B
1
П
16.
фронтально – проецирующая плоскостьА2
(∆ АВС) П2
С2
В2
не имеет проекций
в натуральную величину
х
фронтальная проекция –
в виде прямой,
не параллельной осям OX и ОZ
С1
А1
В1
П2
A2
B2
С2
x
2
Угол наклона к П1
A
2
C
x
0
B
П1
17.
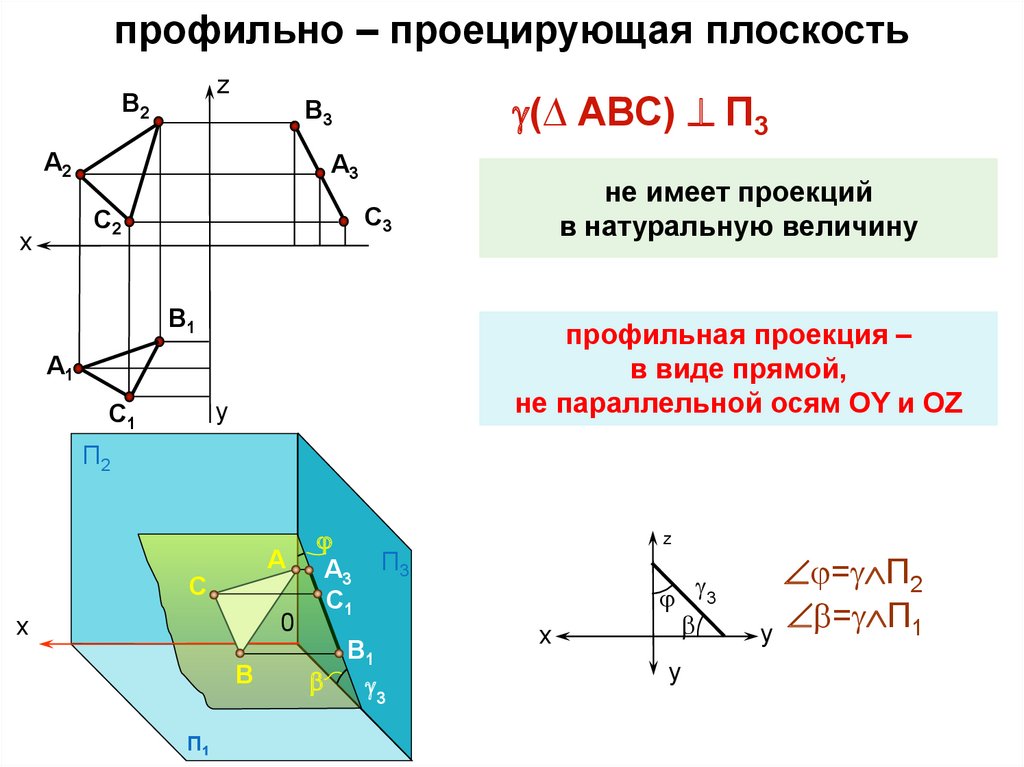
профильно – проецирующая плоскостьz
В2
А2
А3
не имеет проекций
в натуральную величину
С3
С2
х
(∆ АВС) П3
В3
В1
профильная проекция –
в виде прямой,
не параллельной осям OY и ОZ
А1
С1
y
П2
A
C
0
x
B
П1
A3
С1
z
П3
B1
3
x
3
у
= П2
= П1
у
18.
особенности проецирующей плоскостине имеет проекций
в натуральную величину
проецирующая плоскость имеет
одну вырожденную проекцию
в виде прямой линий
на плоскости проекций, к которой она перпендикулярна,
причем эта проекция (в виде прямой)
не параллельна координатным осям,
ограничивающим одноименную плоскость проекций
углы наклона проецирующей плоскости
к плоскостям проекций
проецируются в натуральную величину
на одноименной плоскости проекций
19.
ПРИНАДЛЕЖНОСТЬТОЧКИ и ПРЯМОЙ
ПЛОСКОСТИ
20.
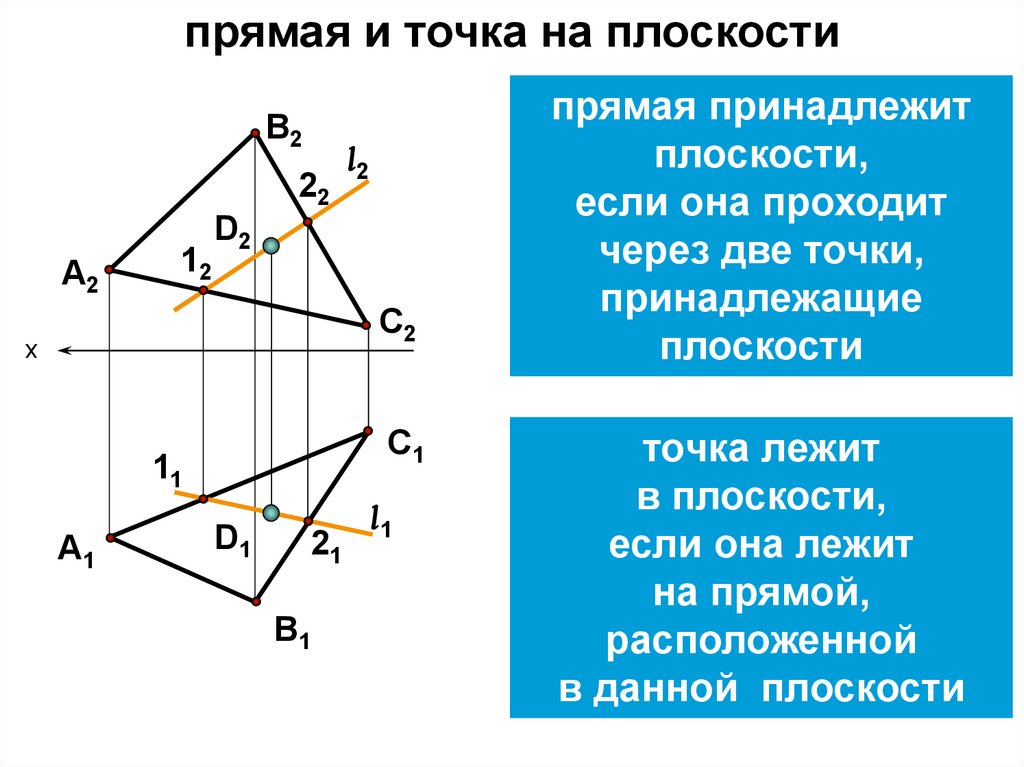
прямая и точка на плоскостиВ2
22
А2
12
l2
D2
С2
х
С1
11
А1
D1
21
В1
l1
прямая принадлежит
плоскости,
если она проходит
через две точки,
принадлежащие
плоскости
точка лежит
в плоскости,
если она лежит
на прямой,
расположенной
в данной плоскости
21.
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ22.
главные линии плоскостиВ2
22
f2
12
А2
h2
С2
х
С1
11
А1
21
В1
f1
h1
h – горизонталь
h ll П1; h ABC
f – фронталь
f ll П2; f ABC
23.
24.
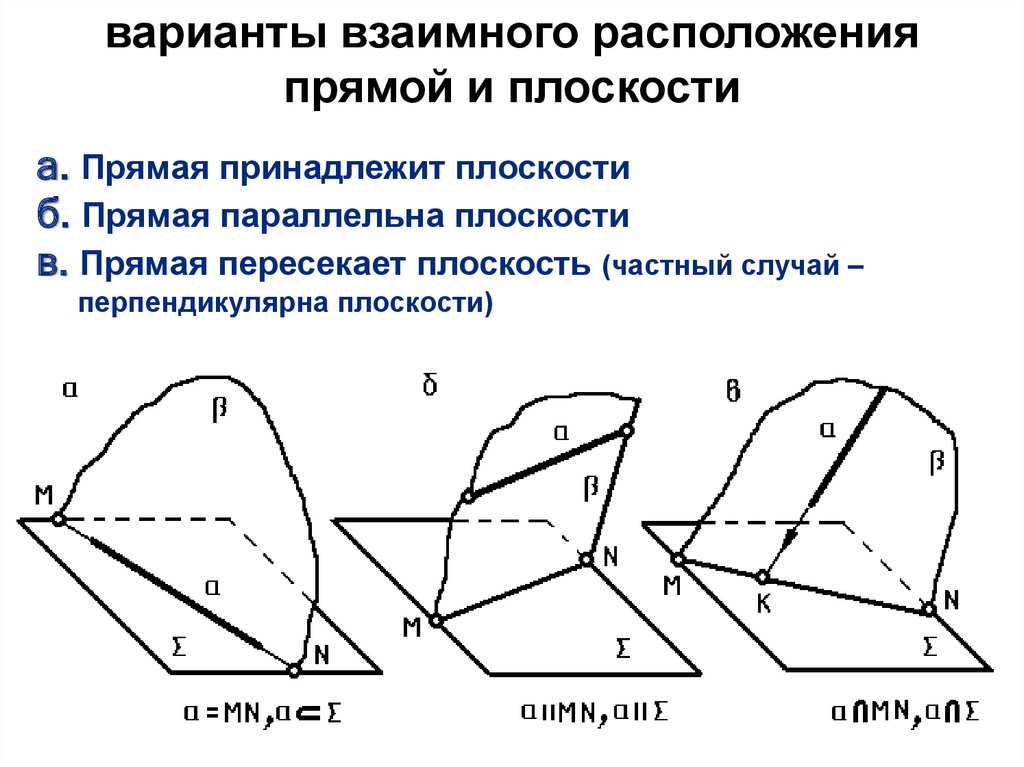
варианты взаимного расположенияпрямой и плоскости
а. Прямая принадлежит плоскости
б. Прямая параллельна плоскости
в. Прямая пересекает плоскость (частный случай –
перпендикулярна плоскости)
25.
условия параллельности прямой и плоскости1 условие
Прямая параллельна плоскости, если она
параллельна какой-либо прямой, принадлежащей
плоскости
a2
12
α (m∩ n)
m
ℓ
a
n2
х
m2
ℓ2
22
m1
n
ℓ (m∩n) ; а ||ℓ ||а
11
a1
n1
ℓ1
21
а1|| ℓ1; а2|| ℓ2 а || (m ∩ n)
26.
условия параллельности прямой и плоскости2 условие
Прямая параллельна плоскости, если она
расположена в другой плоскости, параллельной
заданной плоскости
α || ; а а ||
27.
28.
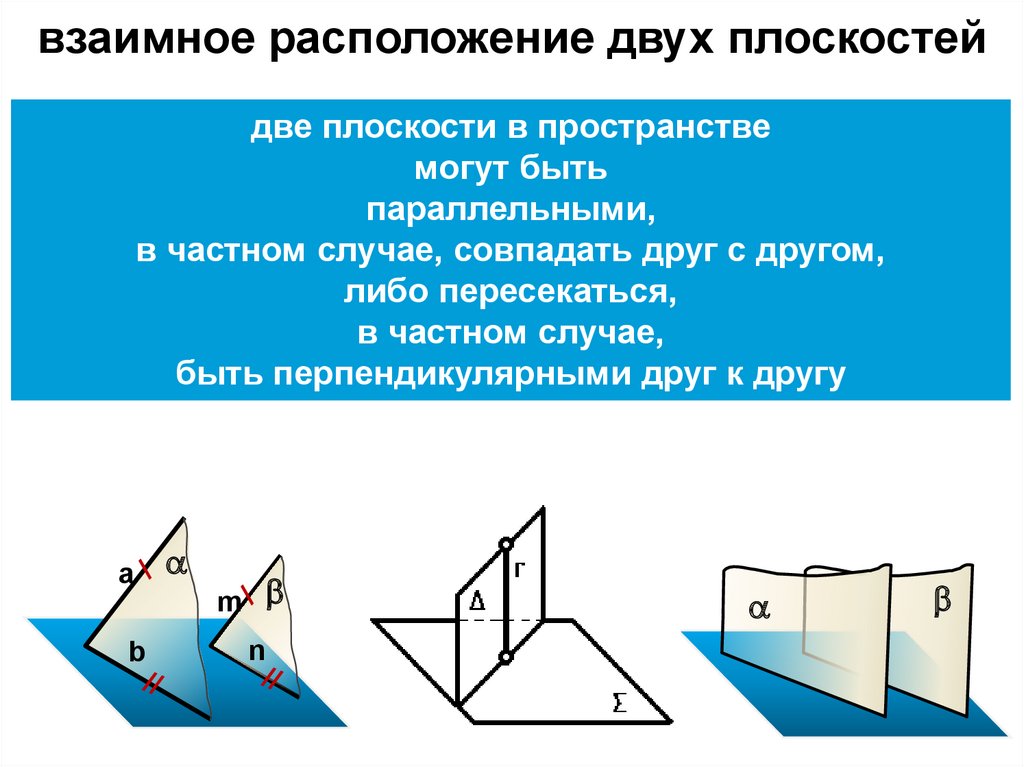
взаимное расположение двух плоскостейдве плоскости в пространстве
могут быть
параллельными,
в частном случае, совпадать друг с другом,
либо пересекаться,
в частном случае,
быть перпендикулярными друг к другу
a
b
m
n
29.
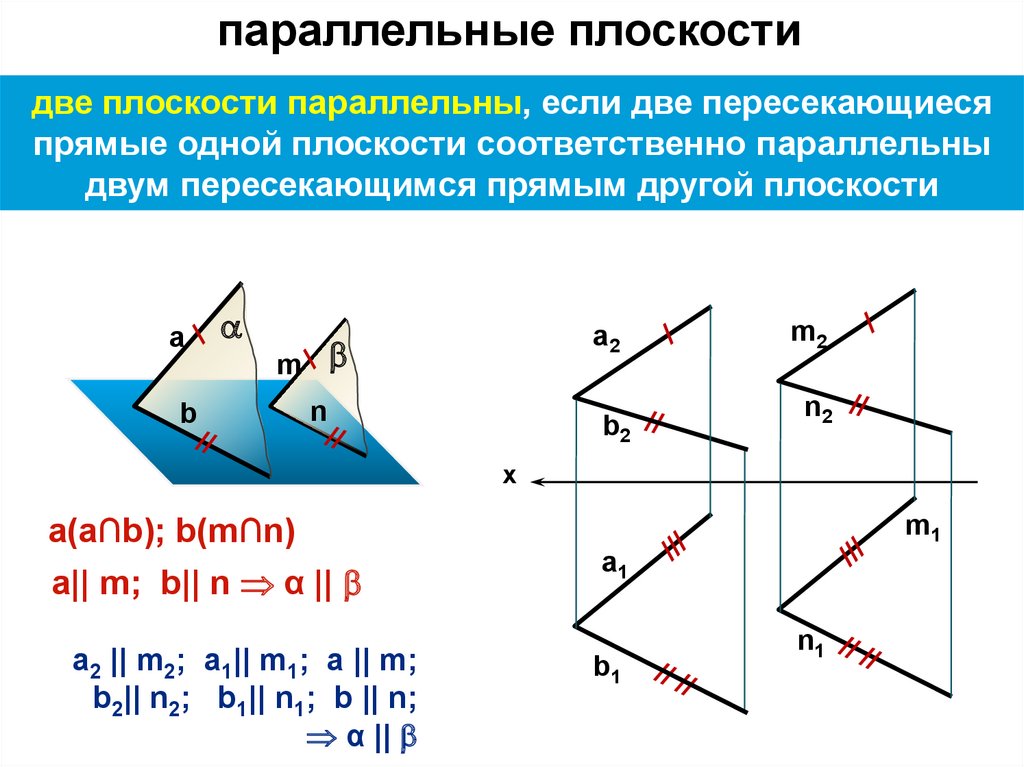
параллельные плоскостидве плоскости параллельны, если две пересекающиеся
прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости
a
a2
m
b
n
b2
m2
n2
х
m1
a(а∩b); b(m∩n)
а|| m; b|| n α ||
а2 || m2; a1|| m1; a || m;
b2|| n2; b1|| n1; b || n;
α ||
a1
b1
n1
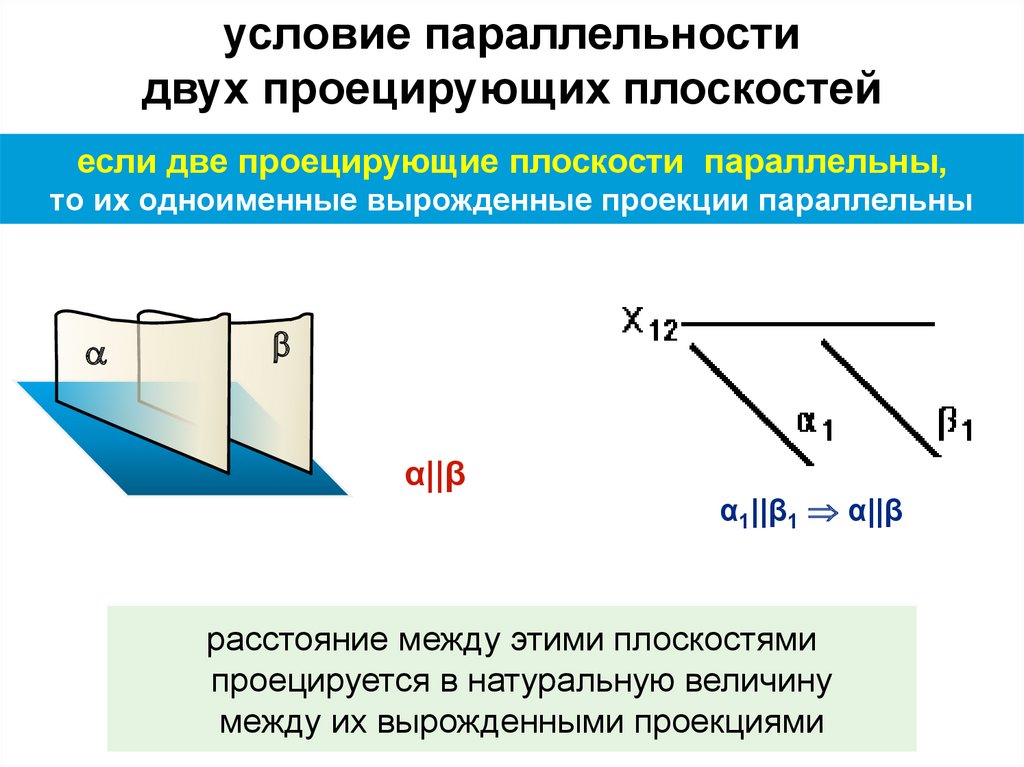
30.
условие параллельностидвух проецирующих плоскостей
если две проецирующие плоскости параллельны,
то их одноименные вырожденные проекции параллельны
α||β
α1||β1 α||β
расстояние между этими плоскостями
проецируется в натуральную величину
между их вырожденными проекциями













 drafting
drafting








