Плоскость. Способы задания плоскости на чертеже

1. Плоскость

доцент кафедры
Инженерная графика и дизайн
НИТУ «МИСиС»
Дербенева О.Л. [email protected]
2015 г.
1

2.

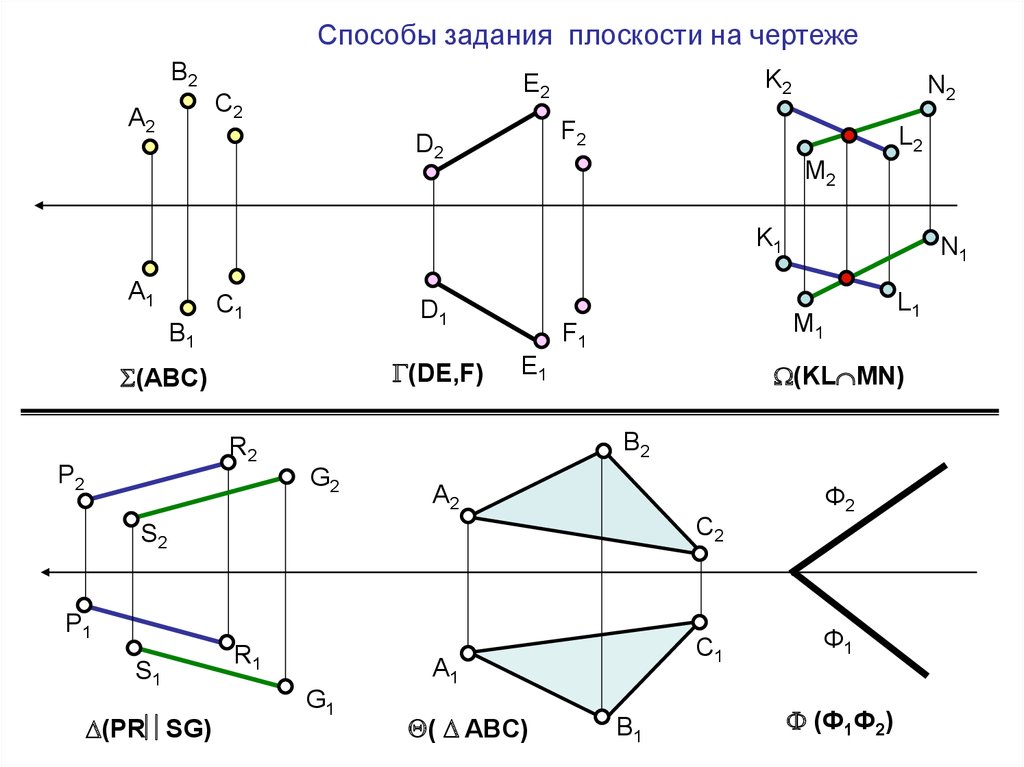
Способы задания плоскости на чертеже
В2
А2
K2
E2
С2
N2
F2
D2
L2
M2
K1
А1
В1
С1
D1
(DE,F)
(ABC)
E1
(KL MN)
В2
G2
А2
С2
S2
P1
S1
(PR SG)
L1
M1
F1
R2
P2
N1
R1
С1
А1
G1
( ABC)
В1
Ф2
Ф1
(Ф1Ф2)

3.

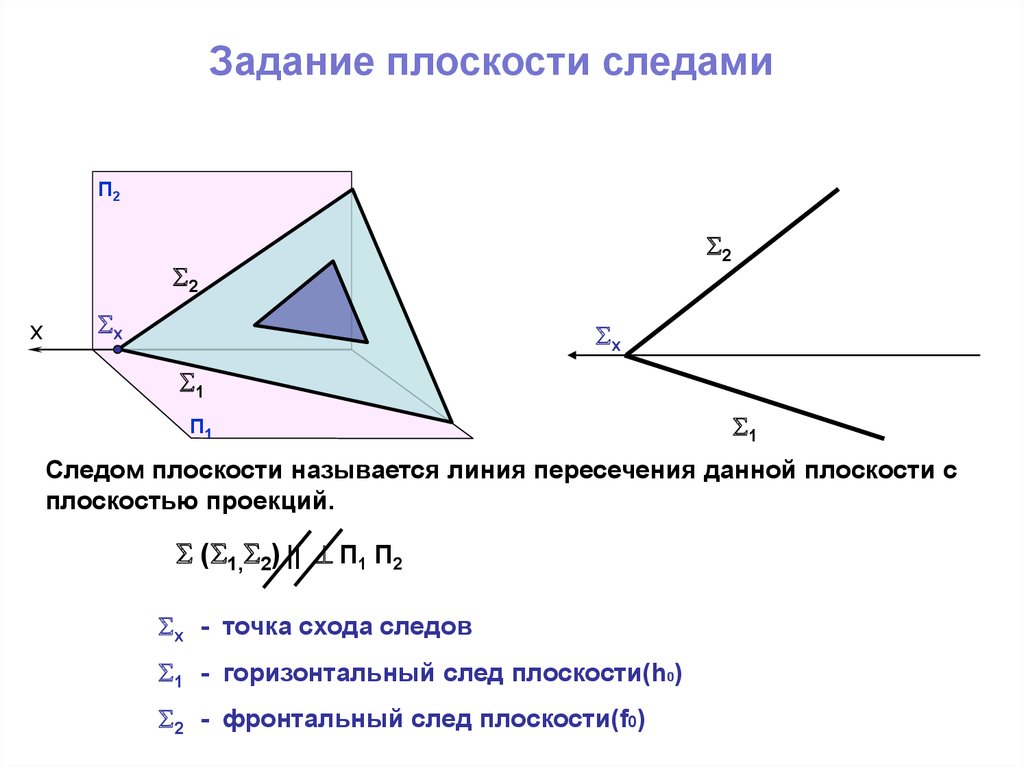
Задание плоскости следами
П2
2
2
х
х
х
1
П1
1
Следом плоскости называется линия пересечения данной плоскости с
плоскостью проекций.
( 1, 2) || П1 П2
х - точка схода следов
1 - горизонтальный след плоскости(h0)
2 - фронтальный след плоскости(f0)

4.

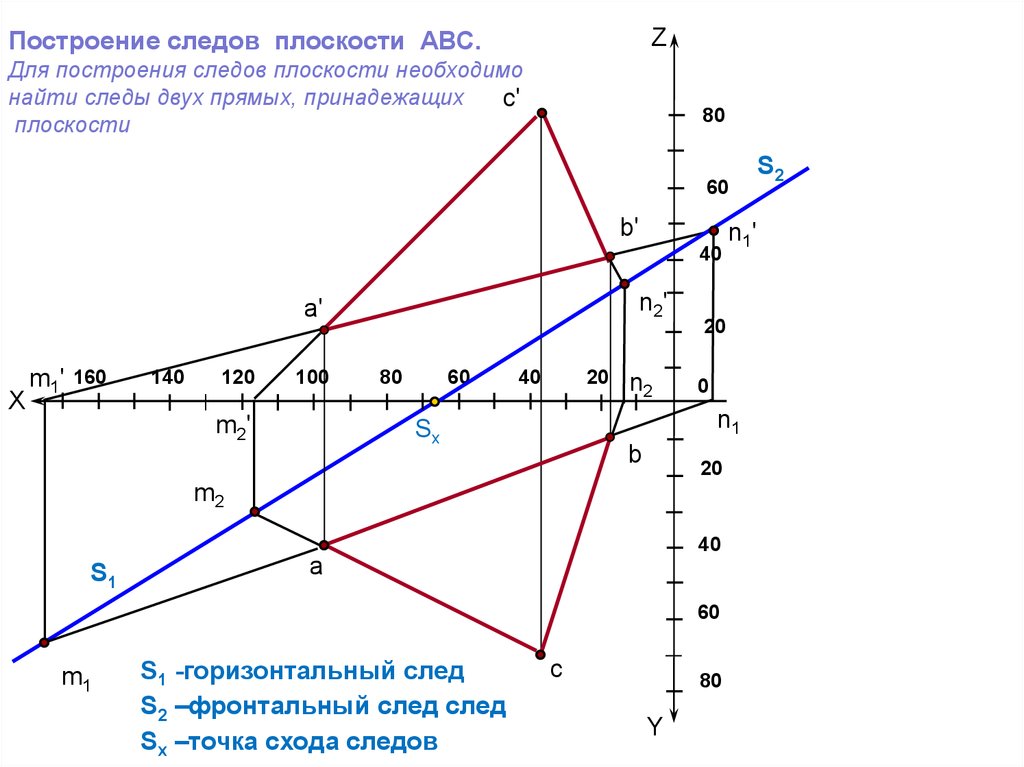
Построение следов плоскости

5.

Построение следов плоскости АВС.
Z
Для построения следов плоскости необходимо
найти следы двух прямых, принадежащих
c'
плоскости
80
60
b'
40
n2'
a'
X
m1 '
160
140
120
100
m2 '
80
60
40
20
n2
20
0
n1
Sx
b
20
m2
40
S1
a
60
m1
S1 -горизонтальный след
S2 –фронтальный след след
Sх –точка схода следов
n1'
c
80
Y
S2

6.

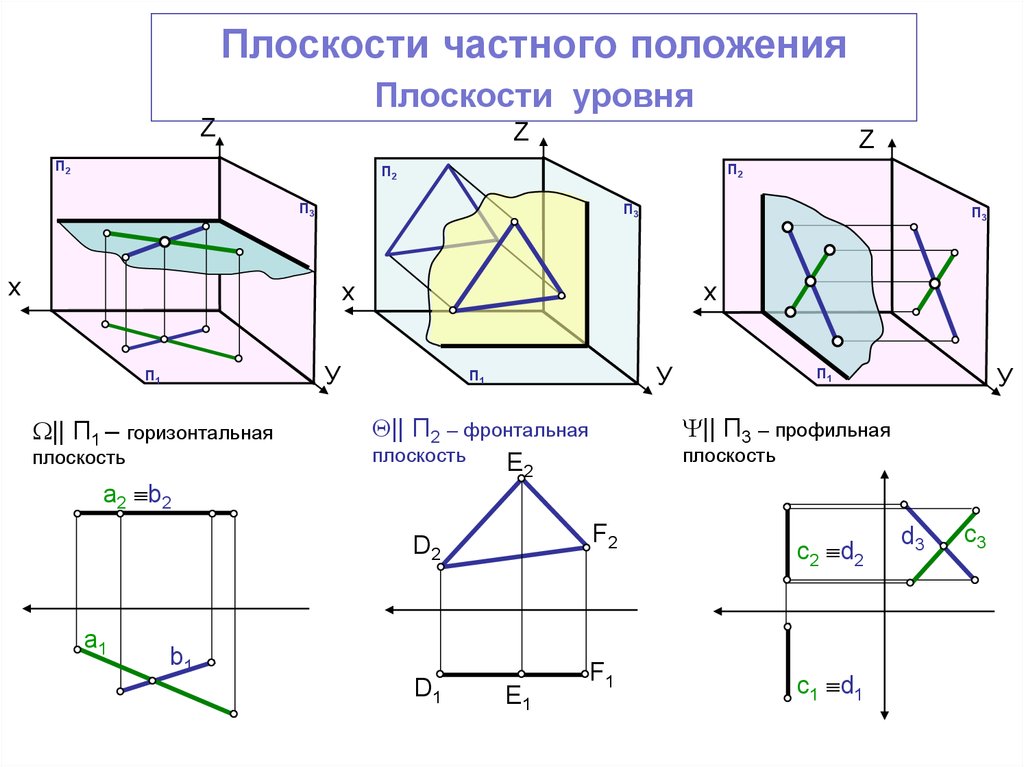
Плоскости частного положения
Плоскости уровня
Z
Z
П2
Z
П2
П2
П3
П3
х
П3
х
х
У
П1
|| П1 – горизонтальная
плоскость
a2 b2
У
П1
|| П2 – фронтальная
плоскость
E2
D2
a1
b1
D1
E1
У
П1
|| П3 – профильная
плоскость
F2
c2 d2
F1
c1 d1
d3
c3

7.

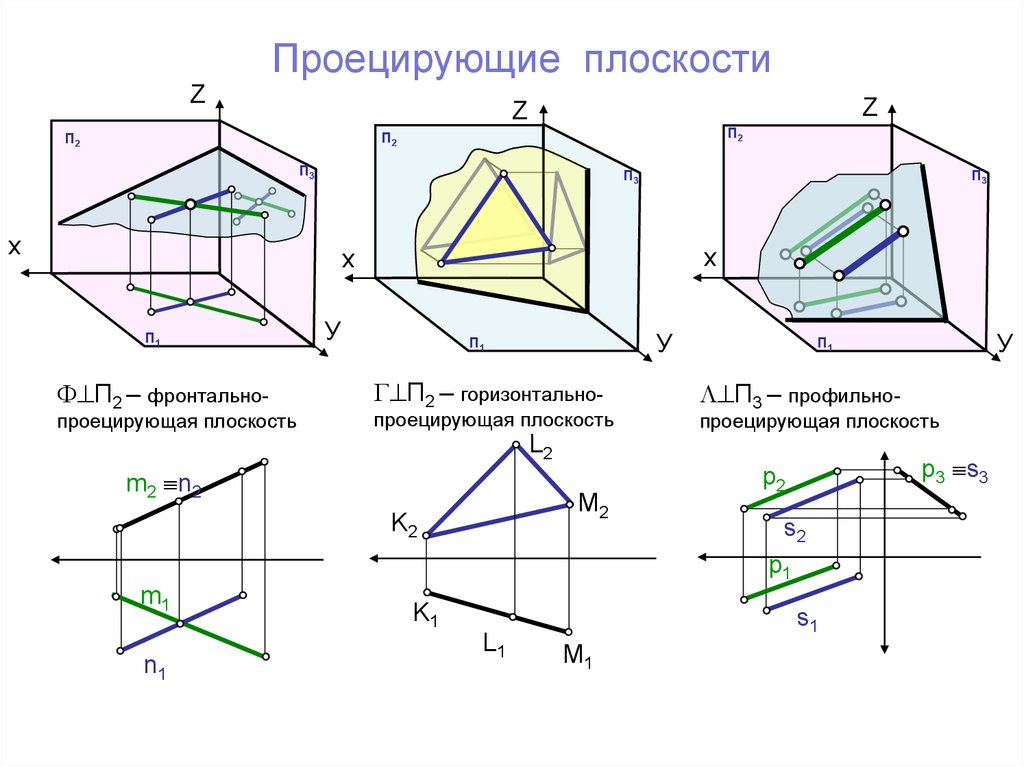
Проецирующие плоскости
Z
Z
Z
П2
П2
П2
П3
П3
х
П3
х
х
П1
П2 – фронтально-
проецирующая плоскость
У
У
П1
П2 – горизонтально-
проецирующая плоскость
П3 – профильно-
проецирующая плоскость
L2
m2 n2
M2
K2
p3 s3
p2
s2
p1
m1
n1
K1
L1
s1
M1
У
П1

8.

Главные линии плоскости:
горизонталь плоскости
фронталь плоскости
линия наибольшего наклона
(ската) плоскости

9.

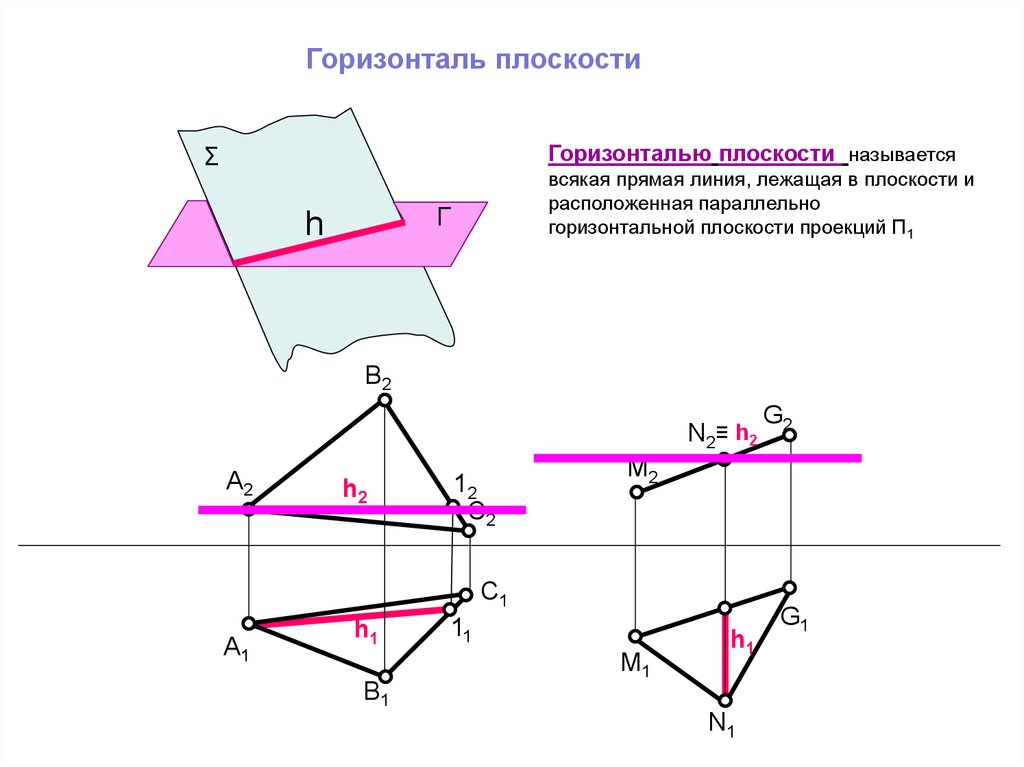
Горизонталь плоскости
Горизонталью плоскости называется
Σ
всякая прямая линия, лежащая в плоскости и
расположенная параллельно
горизонтальной плоскости проекций П1
Г
h
B2
N2≡ h2
A2
h2
12
C2
M2
C1
A1
h1
G2
11
M1
h1
B1
N1
G1

10.

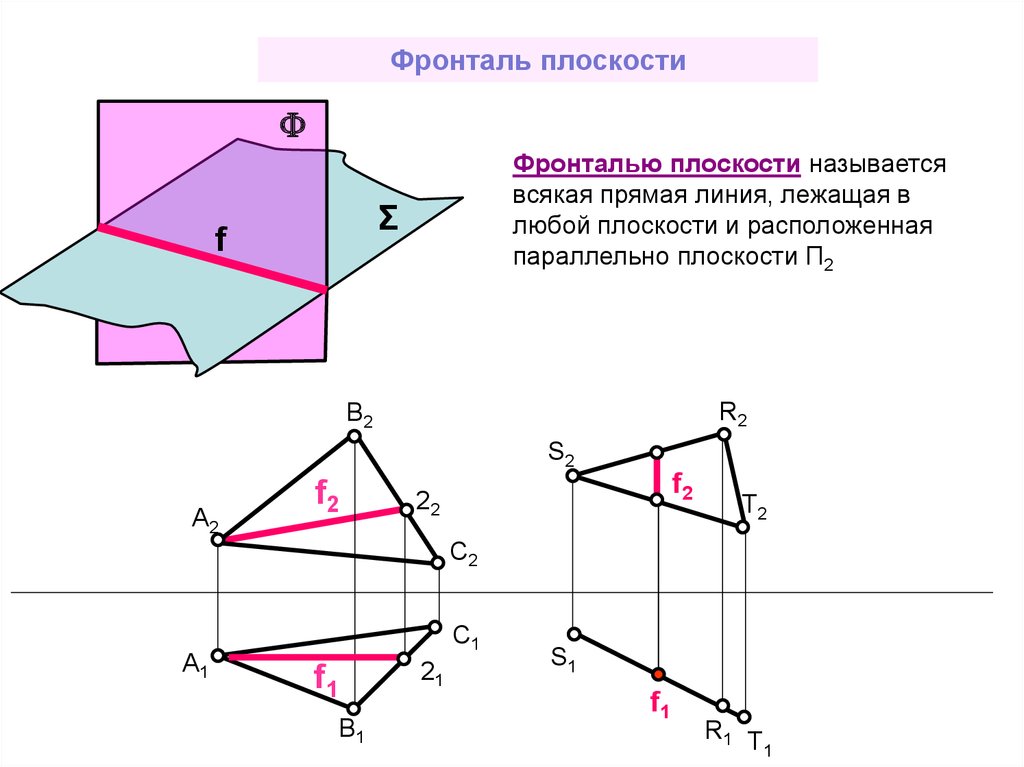
Фронталь плоскости
Фронталью плоскости называется
всякая прямая линия, лежащая в
любой плоскости и расположенная
параллельно плоскости П2
Σ
f
R2
B2
S2
A2
f2
f2
22
T2
C2
A1
C1
21
f1
B1
S1
f1
R1 T
1

11.

В плоскости, заданной
точками А, В, С провести
горизонталь h и фронталь f
Z
c2
80
f2
60
22
h2
12
b2
40
a2
X
160
140
120
20
100
80
60
40
20
0
b1
h ll П1; h ABC; h2 ll x;
f2 ll П2; f ABC; f1 ll x;
20
f1
a1
40
21
h1
11
60
c1
80
Y

12.

Линия наибольшего наклона (ската) плоскости
Л и нии на и б о л ьше г о с к а т а –это прямые, проведенные в
плоскости перпендикулярно её горизонталям.
По углу наклонения линии наибольшего ската к плоскости П1
определяют двугранный угол наклона плоскости к
горизонтальной плоскости проекций.
Правило построения линии наибольшего ската плоскости
Горизонтальная проекция линии наибольшего ската
плоскости перпендикулярна горизонтальным проекциям
горизонталей плоскости.

13.

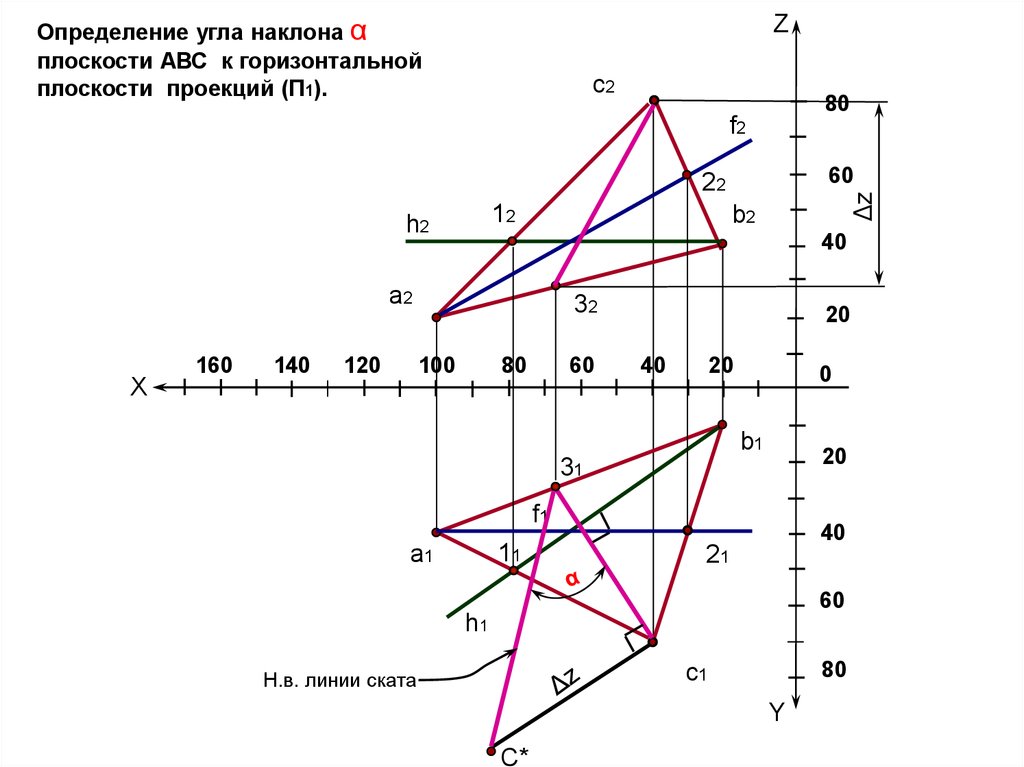
Z
Определение угла наклона α
плоскости АВС к горизонтальной
плоскости проекций (П1).
c2
80
f2
60
12
h2
b2
40
a2
X
160
140
120
Δz
22
32
100
80
60
20
40
20
0
b1
20
31
f1
11
a1
40
21
60
h1
80
c1
Н.в. линии ската
Y
C*

14.

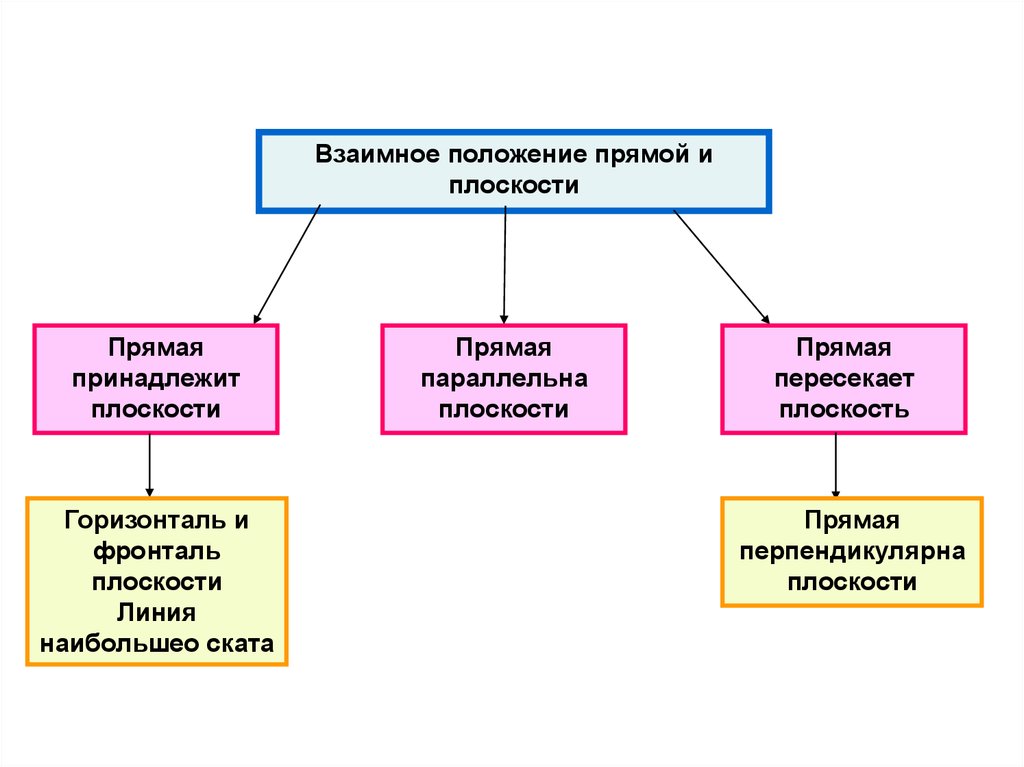
Взаимное положение прямой и
плоскости
Прямая
принадлежит
плоскости
Горизонталь и
фронталь
плоскости
Линия
наибольшео ската
Прямая
параллельна
плоскости
Прямая
пересекает
плоскость
Прямая
перпендикулярна
плоскости

15.

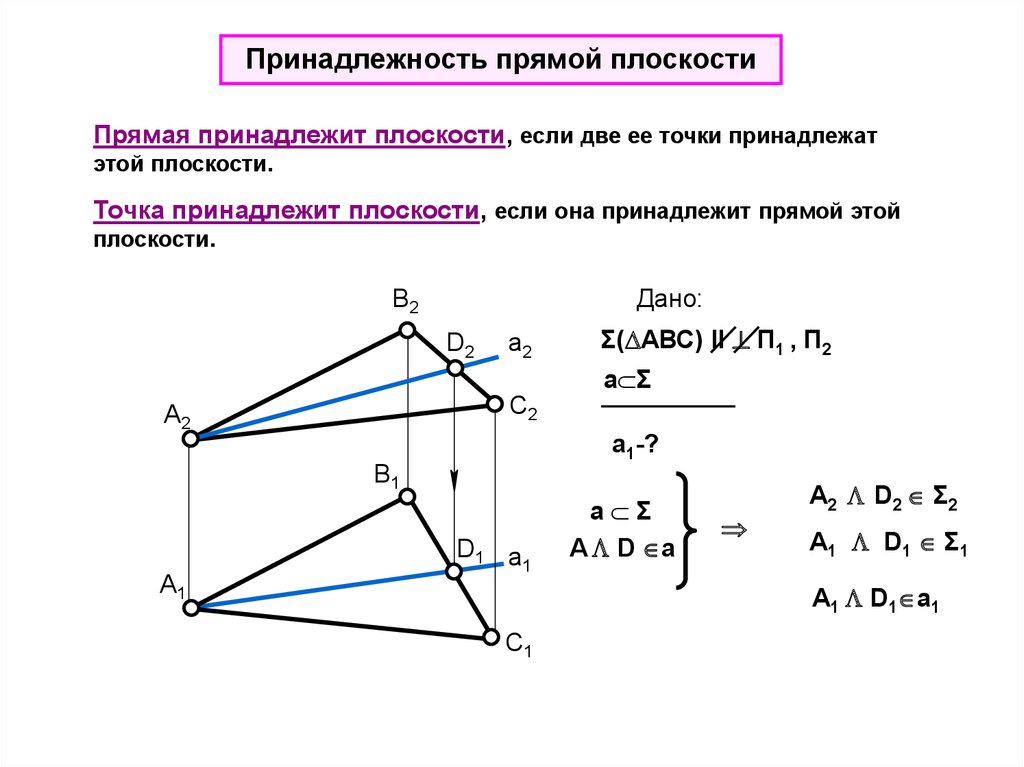
Принадлежность прямой плоскости
Прямая принадлежит плоскости, если две ее точки принадлежат
этой плоскости.
Точка принадлежит плоскости, если она принадлежит прямой этой
плоскости.
В2
Дано:
D2
a2
С2
А2
a Σ
a1-?
В1
А1
Σ( АВС) ll П1 , П2
D1 a
1
a Σ
A D a
A2 D2 Σ2
A1 D1 Σ1
A1 D1 a1
С1

16.

Принадлежность прямой плоскости
Прямая принадлежит плоскости, если две ее точки принадлежат
следам этой плоскости.
Точка принадлежит плоскости, если она принадлежит прямой этой
плоскости.
NM P
D P
n ABC
D ABC

17.

Определить
взаимоположение точек
М и N и плоскости ABC
B2
N2
Дано:
( АВС) || П1 П2
М2
12
М ?
A2
C2
N ?
М
М2
(A212)
М1 (A111)
(A1)
A1
C1
N1
B1
11
N N2 (A212)
N1 (A111)
М1

18.

B2
12
A2
C2
22
Дано:
(АВСDE) || П1 П2
1 - ?
D2
E2
B1
11
C1
A1
21
E1
D1
Определить недостающие
проекции точек C1 и D1
плоскости ABCDE.

19.

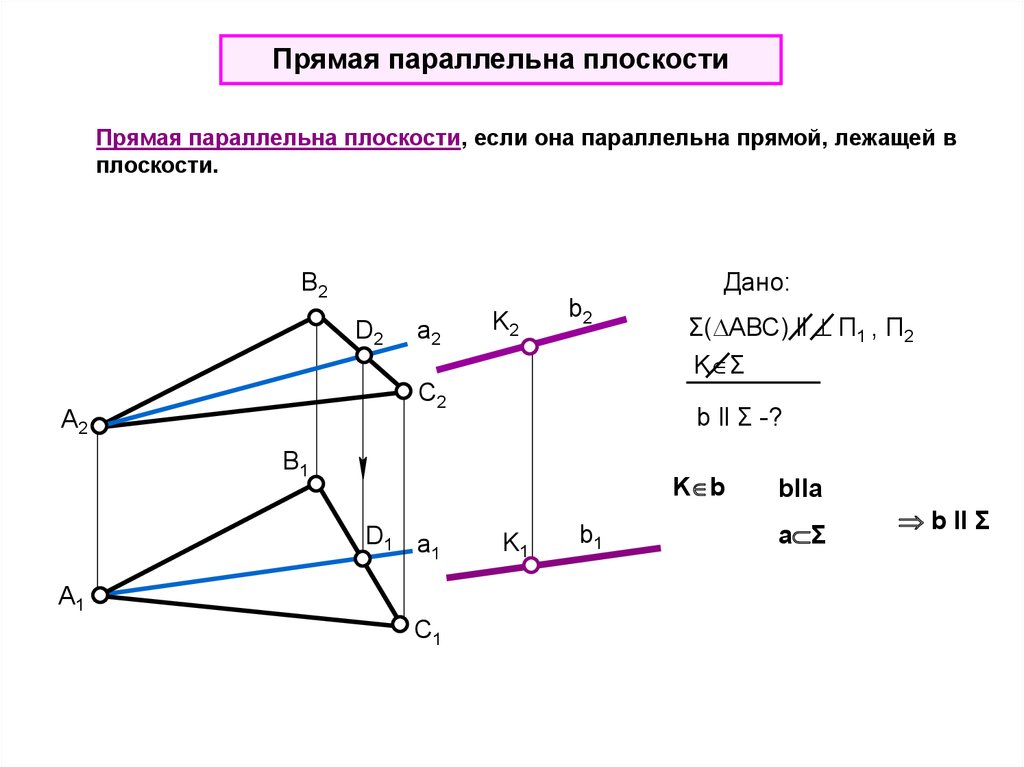
Прямая параллельна плоскости
Прямая параллельна плоскости, если она параллельна прямой, лежащей в
плоскости.
В2
Дано:
D2
a2
K2
b2
С2
А2
Σ( АВС) ll П1 , П2
K Σ
b ll Σ -?
В1
K b
D1 a
1
А1
С1
K1
b1
blla
a Σ
b ll Σ

20.

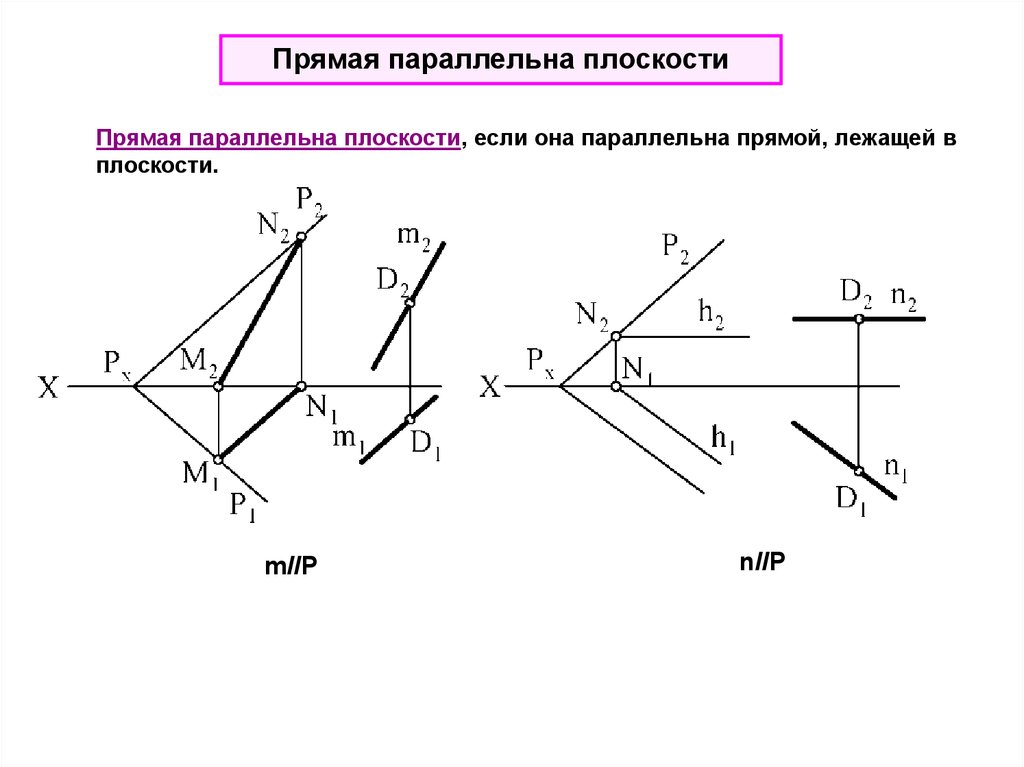
Прямая параллельна плоскости
Прямая параллельна плоскости, если она параллельна прямой, лежащей в
плоскости.
mIIP
nIIP

21.

22.

Прямая пересекает плоскость
Дано:
a
K
Г
m
Σ - плоскость
а – прямая линия
а Σ
а Σ = К - ?
Σ
1. Заключаем прямую
а во вспомогательную плоскость Г
2. Находим линию пересечения заданной плоскости Σ
и вспомогательной плоскости
3. Определяем точку пересечения
И линии m
Г
K заданной линии а
4. Определяем видимость прямой а

23.

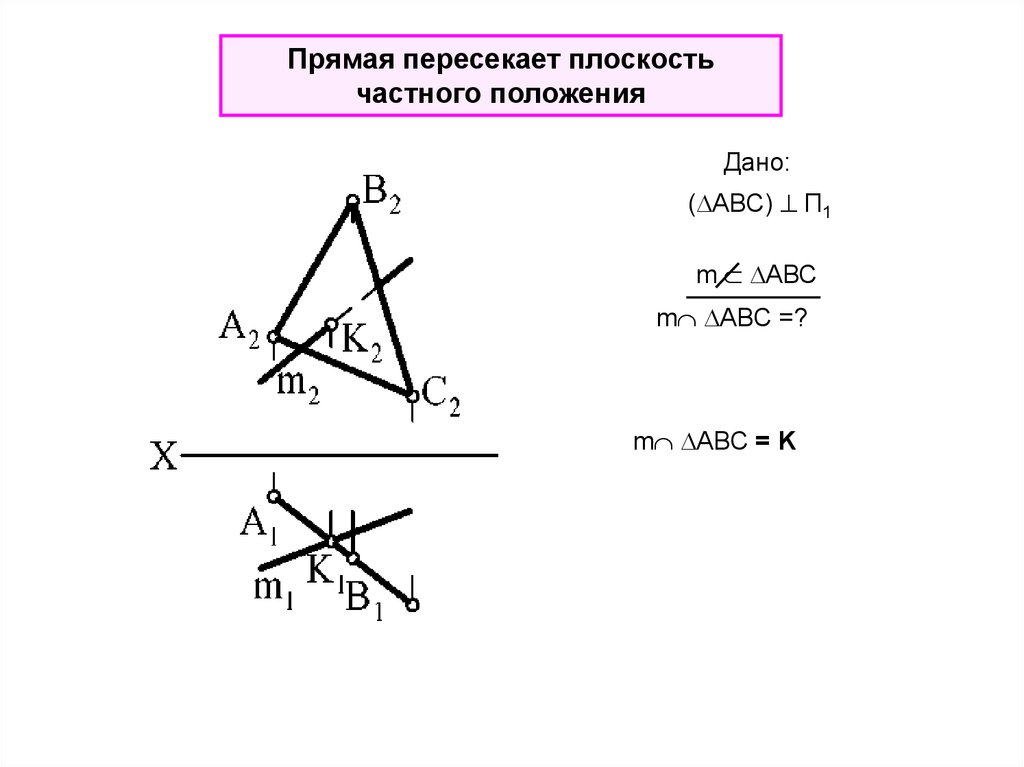
Прямая пересекает плоскость
частного положения
Дано:
( АВС) П1
m АВС
m АВС =?
m АВС = K

24.

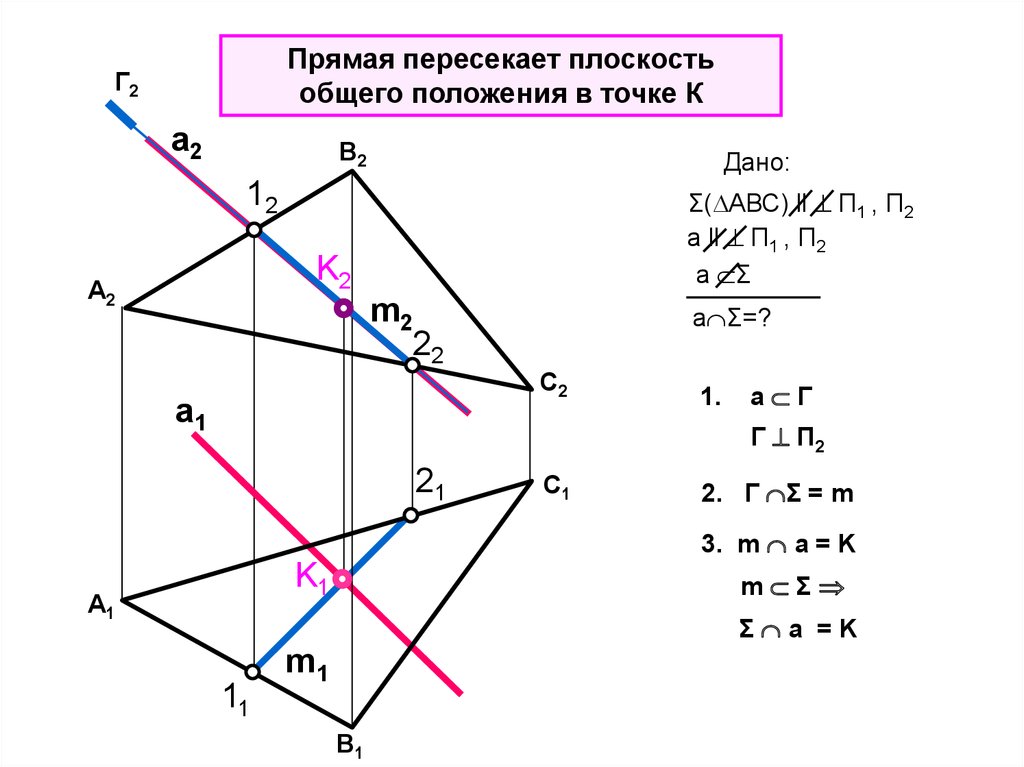
Прямая пересекает плоскость
общего положения в точке К
Г2
а2
B2
Дано:
12
Σ( АВС) ll П1 , П2
a ll П1 , П2
a Σ
K2
А2
m2
22
a Σ=?
C2
а1
1.
а Г
Г П2
21
C1
2. Г Σ = m
3. m a = K
K1
А1
m Σ
Σ a =K
11
m1
B1

25.

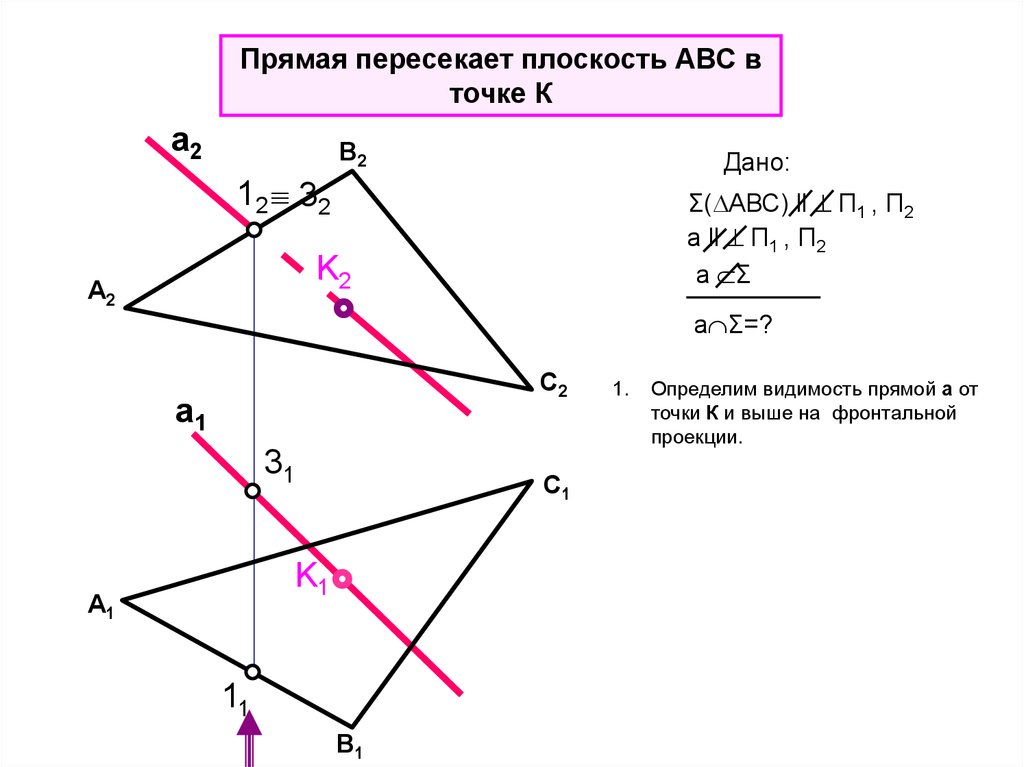
Прямая пересекает плоскость АВС в
точке К
а2
B2
Дано:
12 32
Σ( АВС) ll П1 , П2
a ll П1 , П2
a Σ
K2
А2
a Σ=?
C2
а1
31
C1
K1
А1
11
B1
1.
Определим видимость прямой а от
точки К и выше на фронтальной
проекции.

26.

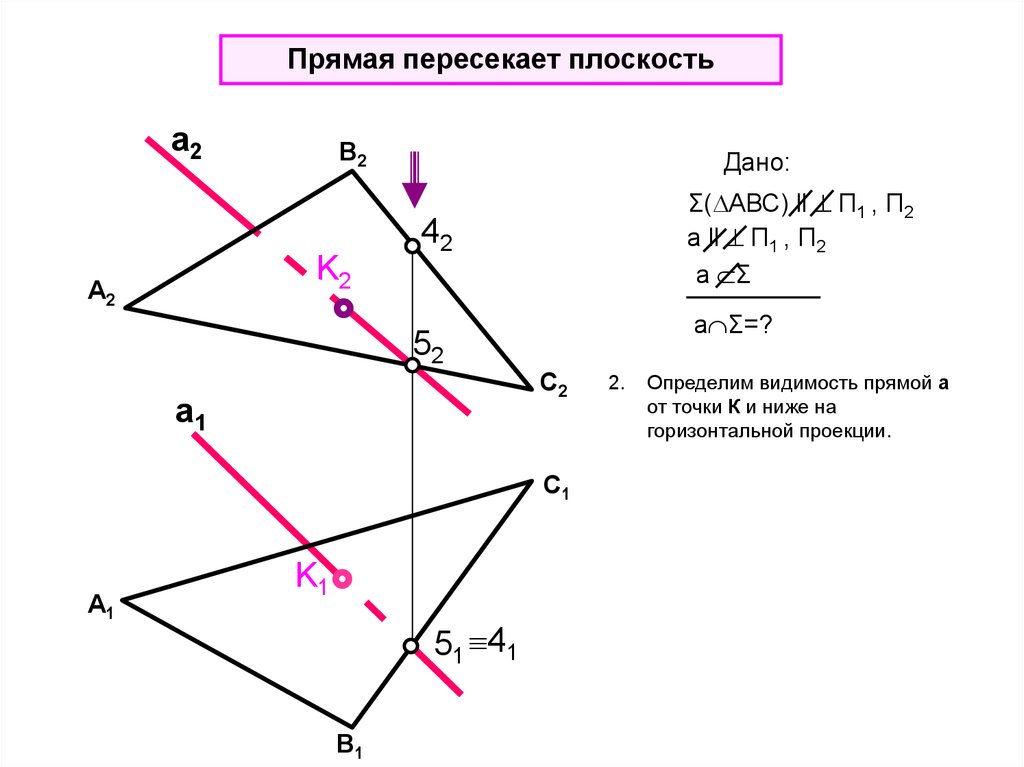
Прямая пересекает плоскость
а2
B2
K2
А2
Дано:
Σ( АВС) ll П1 , П2
a ll П1 , П2
a Σ
42
a Σ=?
52
C2
а1
C1
А1
K1
51 41
B1
2.
Определим видимость прямой а
от точки К и ниже на
горизонтальной проекции.

27.

Прямая пересекает плоскость общего положения
Г2
B2
А2
l2
22
K2
m2
12
D2
C2
1.
l Г
Г П2
D1
11
А1
m1
K1
l1
2. Г Σ = m
B1
3. m l = K
m Σ
C1
21
Σ a =K

28.

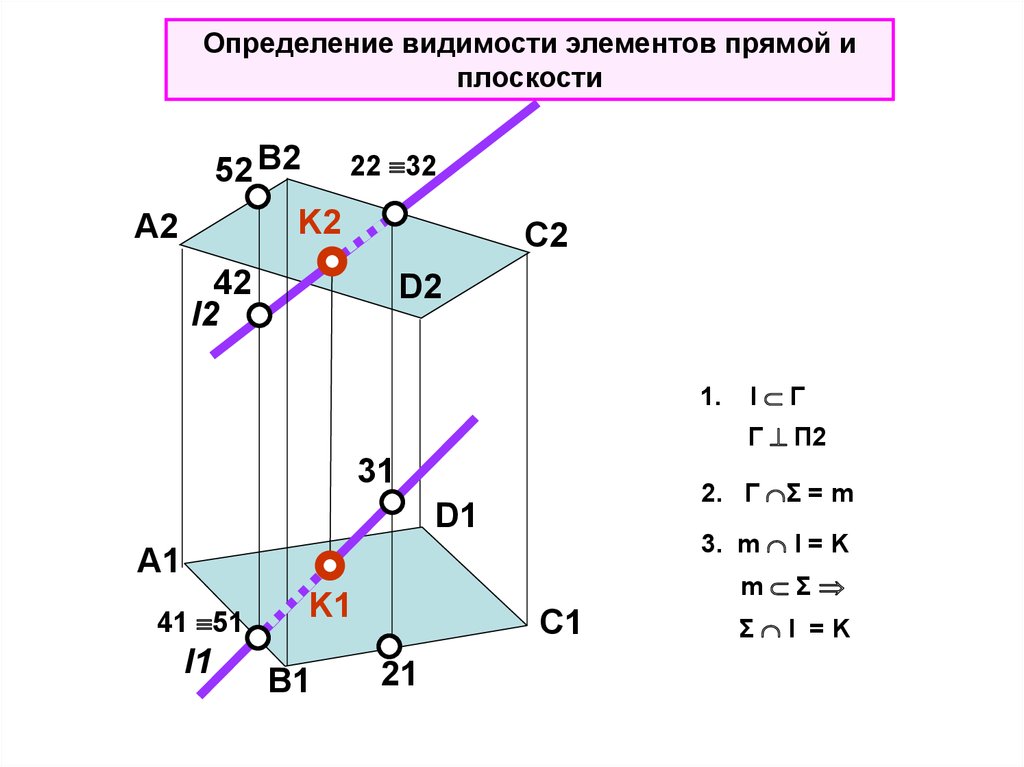
Определение видимости элементов прямой и
плоскости
52 B2
А2
22 32
K2
C2
42
l2
D2
1.
l Г
Г П2
31
2. Г Σ = m
D1
3. m l = K
А1
41 51
l1
m Σ
K1
B1
C1
21
Σ l =K

29.

30.

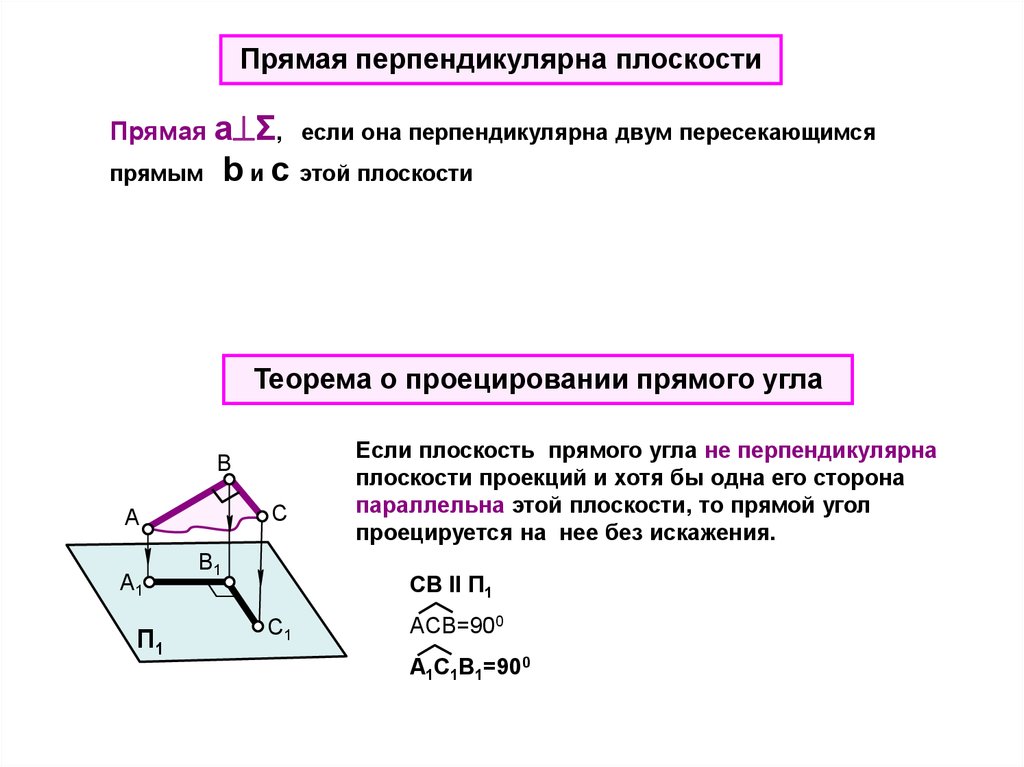
Прямая перпендикулярна плоскости
Прямая а Σ, если она перпендикулярна двум пересекающимся
b и c этой плоскости
прямым
Теорема о проецировании прямого угла
B
C
A
A1
П1
B1
Если плоскость прямого угла не перпендикулярна
плоскости проекций и хотя бы одна его сторона
параллельна этой плоскости, то прямой угол
проецируется на нее без искажения.
CB ll П1
C1
ACB=900
A1C1B1=900

31.

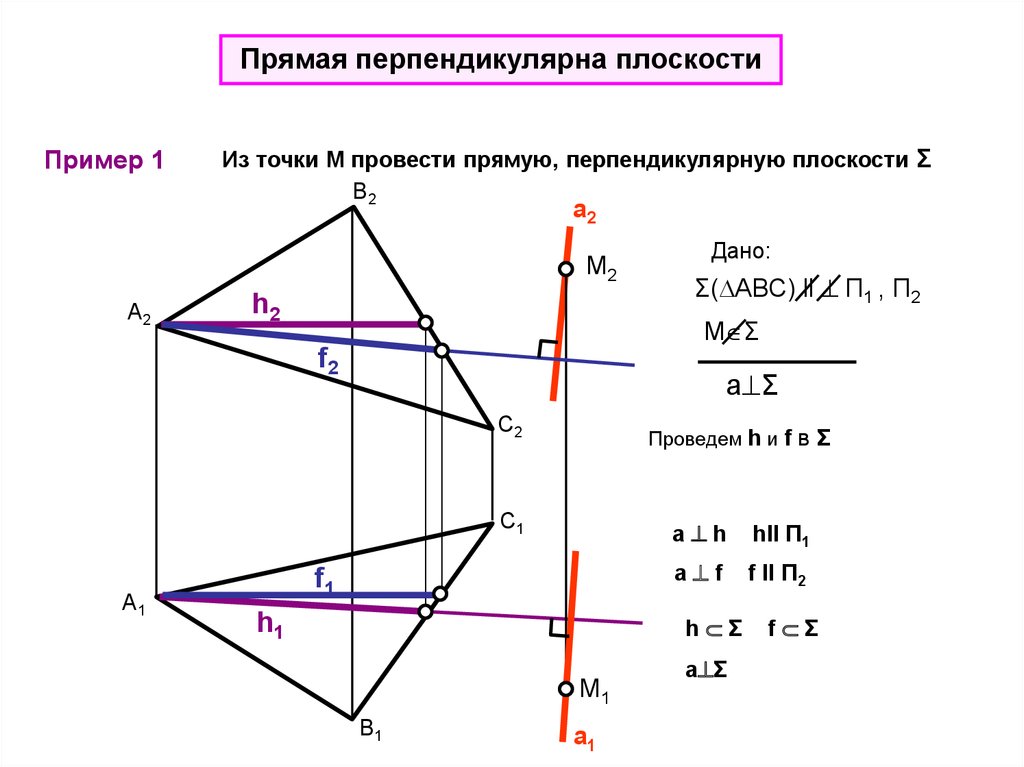
Прямая перпендикулярна плоскости
Пример 1
Из точки М провести прямую, перпендикулярную плоскости Σ
B2
a2
M2
A2
h2
Дано:
Σ( АВС) ll П1 , П2
M Σ
f2
a Σ
C2
Проведем h и f в Σ
C1
A1
f1
h1
a h
hll П1
a f
f ll П2
h Σ
M1
B1
a1
a Σ
f Σ

32.

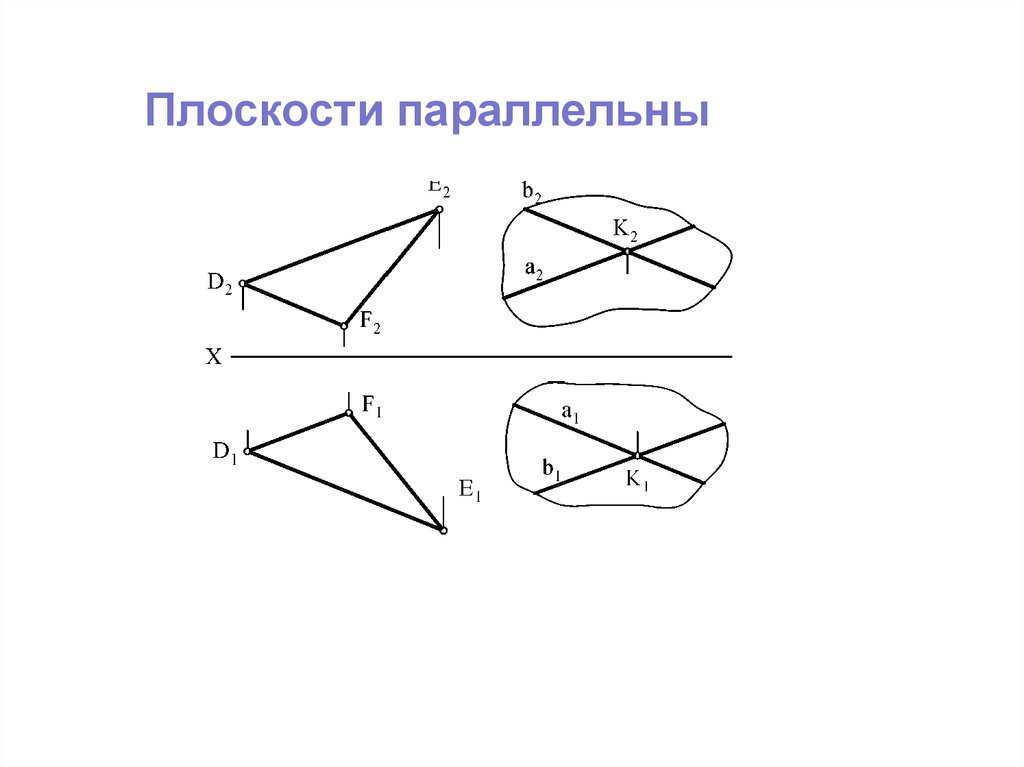
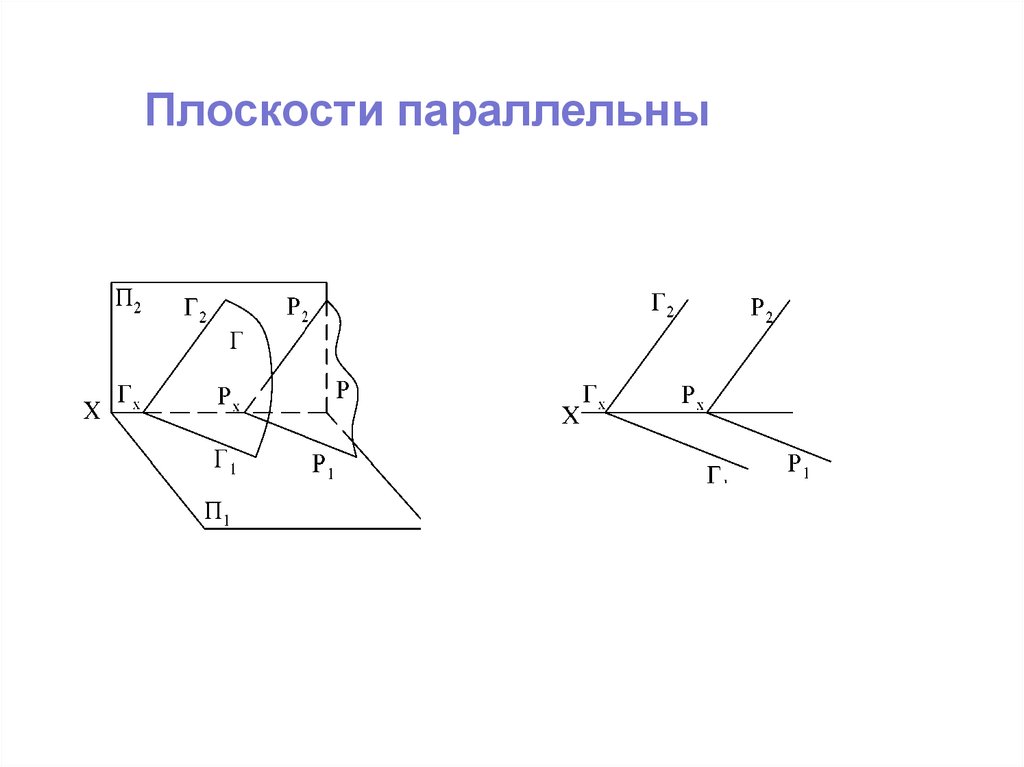
Взаимоположение плоскостей
Плоскости параллельны
Плоскости пересекаются

33.

Плоскости параллельны

34.

Плоскости параллельны

35.

Пересечение плоскости частного положения с
плоскостью общего положения

36.

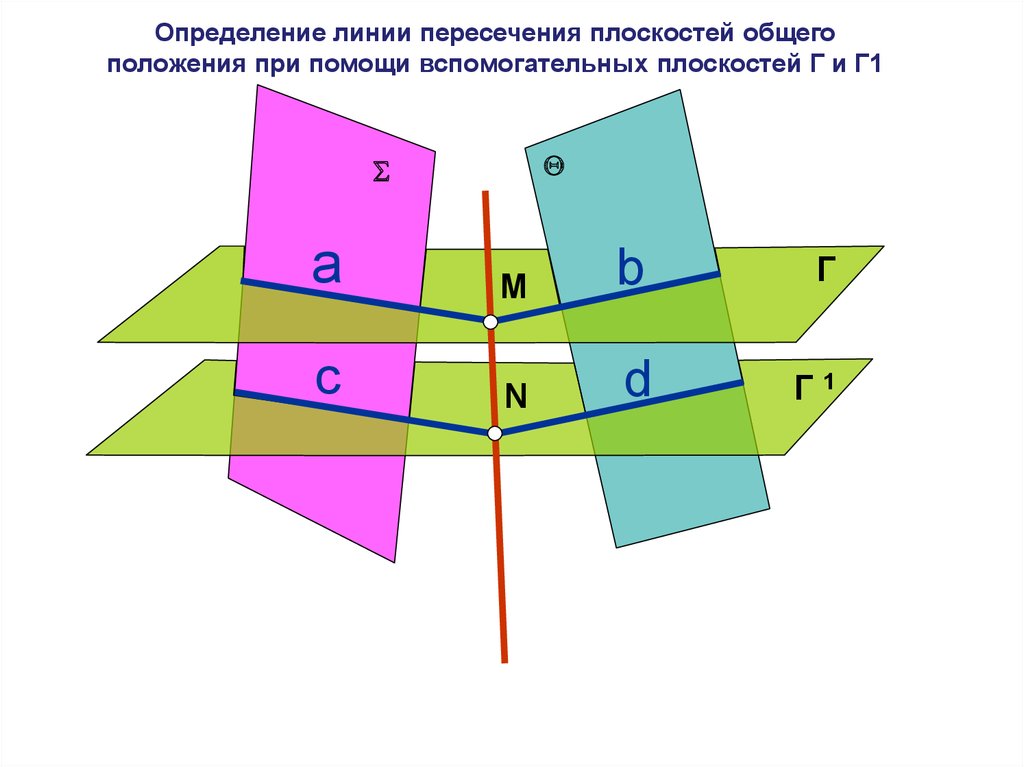
Определение линии пересечения плоскостей общего
положения при помощи вспомогательных плоскостей Г и Г1
а
М
b
Г
c
N
d
Г1

37.

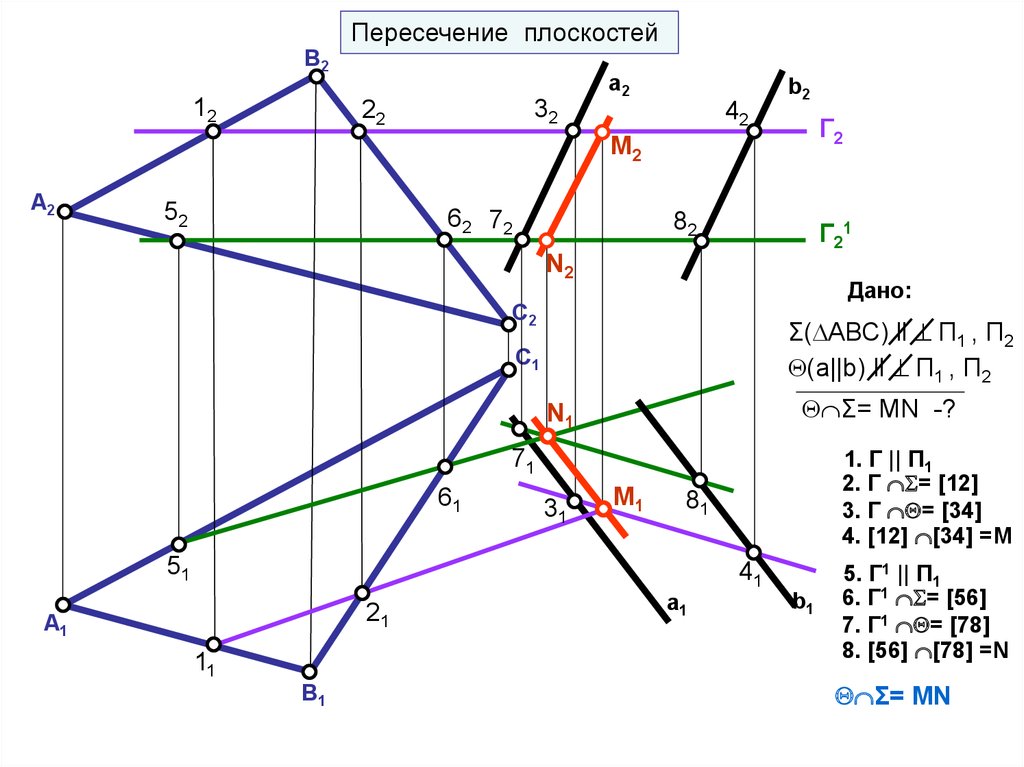
Пересечение плоскостей
B2
12
32
22
а2
42
b2
Г2
M2
A2
52
62 72
82
Г21
N2
Дано:
C2
Σ( АВС) ll П1 , П2
(а||b) ll П1 , П2
C1
Σ= MN -?
N1
1. Г || П1
2. Г = [12]
3. Г = [34]
4. [12] [34] =M
71
61
31
M1
81
51
21
A1
11
B1
а1
41
b1
5. Г1 || П1
6. Г1 = [56]
7. Г1 = [78]
8. [56] [78] =N
Σ= MN

38.

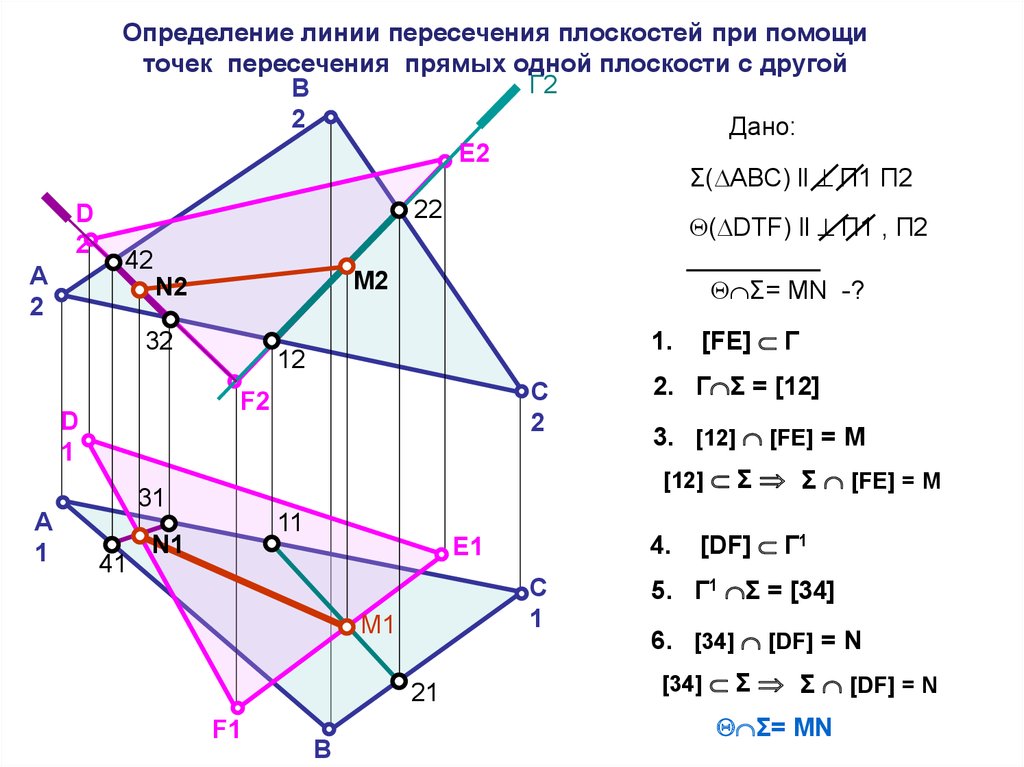
Определение линии пересечения плоскостей при помощи
точек пересечения прямых одной плоскости с другой
Г1
Г
N
M

39.

D
2
A
2
Определение линии пересечения плоскостей при помощи
точек пересечения прямых одной плоскости с другой
Г2
B
2
Дано:
E2
Σ( АВС) ll П1 П2
22
( DTF) ll П1 , П2
42
M2
N2
Σ= MN -?
32
1.
12
C
2
F2
D
1
41
2. Г Σ = [12]
3. [12] [FE] = M
[12] Σ Σ [FE] = M
31
A
1
[FE] Г
11
N1
4.
E1
C
1
M1
21
F1
B
[DF] Г1
5. Г1 Σ = [34]
6. [34] [DF] = N
[34] Σ Σ [DF] = N
Σ= MN

40.

D
2
A
2
D
1
Определение линии пересечения плоскостей при помощи
точек пересечения прямых одной плоскости с другой
Г2
B
2
Дано:
E2
Σ( АВС) ll П1 ,
П2
22
72
62
( DTF) ll П1 ,
42=52
П2
M2
N2
Σ= MN -?
82
1. [FE] Г
32
12
2. Г Σ = [12]
C
F2
2
3. [12] [FE] = M
[12] Σ Σ [FE] = M
31
A
1
41
11
N1
4.
E1
61
M1
71
81
21
F1
B
C
1
[DF] Г1
5. Г1 Σ = [34]
6. [34] [DF] = N
[34] Σ Σ [DF] = N
Σ= MN