Similar presentations:
Образование линии в пространстве и задание ее на чертеже (лекция 2)
1.
Лекция 2Образование линии
в пространстве
и задание ее на чертеже
2.
Линию следует рассматриватькак множество последовательных
положений точки, перемещающейся
в пространстве
3.
Прямая4.
Прямая линия получаетсяпри прямолинейном движении точки
без изменения направления движения
5.
Совокупность элементов, задающихпрямую в пространстве, называется
определителем прямой
6.
ВА
а (А, В)
Рис. 2.1
7.
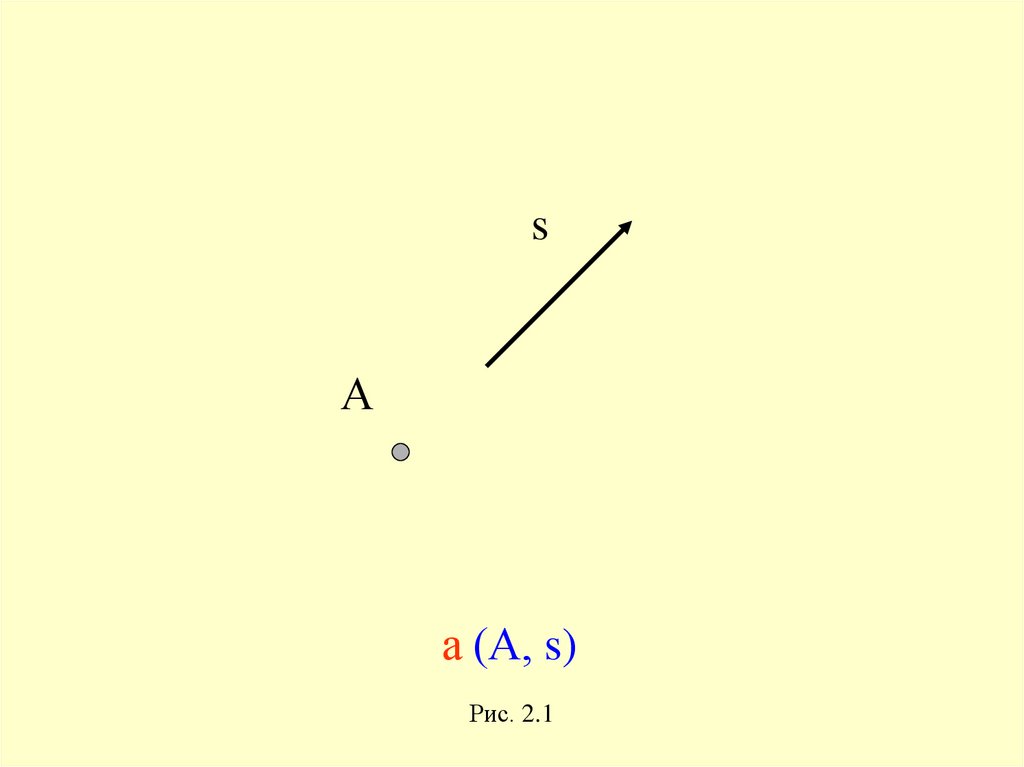
sА
а (А, s)
Рис. 2.1
8.
ВА
а ( [АВ] )
Рис. 2.1
9.
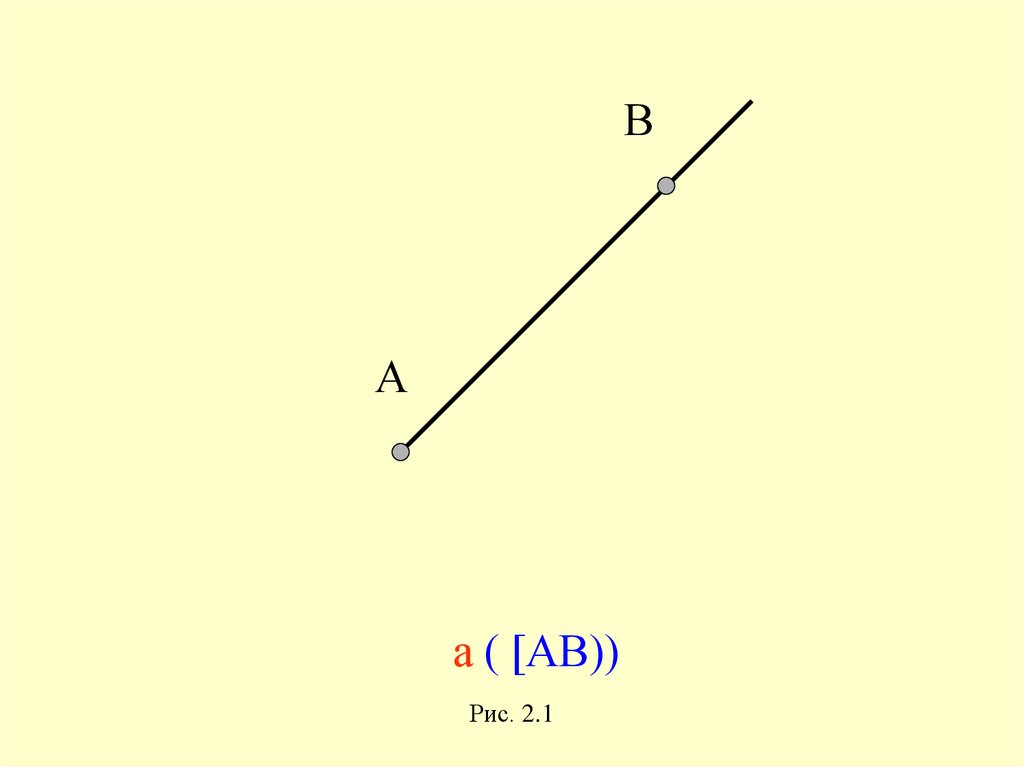
ВА
а ( [АВ))
Рис. 2.1
10.
ВА
а ((АВ))
Рис. 2.1
11.
Основные свойства прямоугольногопроецирования:
1.
Точка проецируется в точку, прямая – в прямую,
плоская фигура – в плоскую фигуру, объемные тела
– в плоские фигуры.
2.
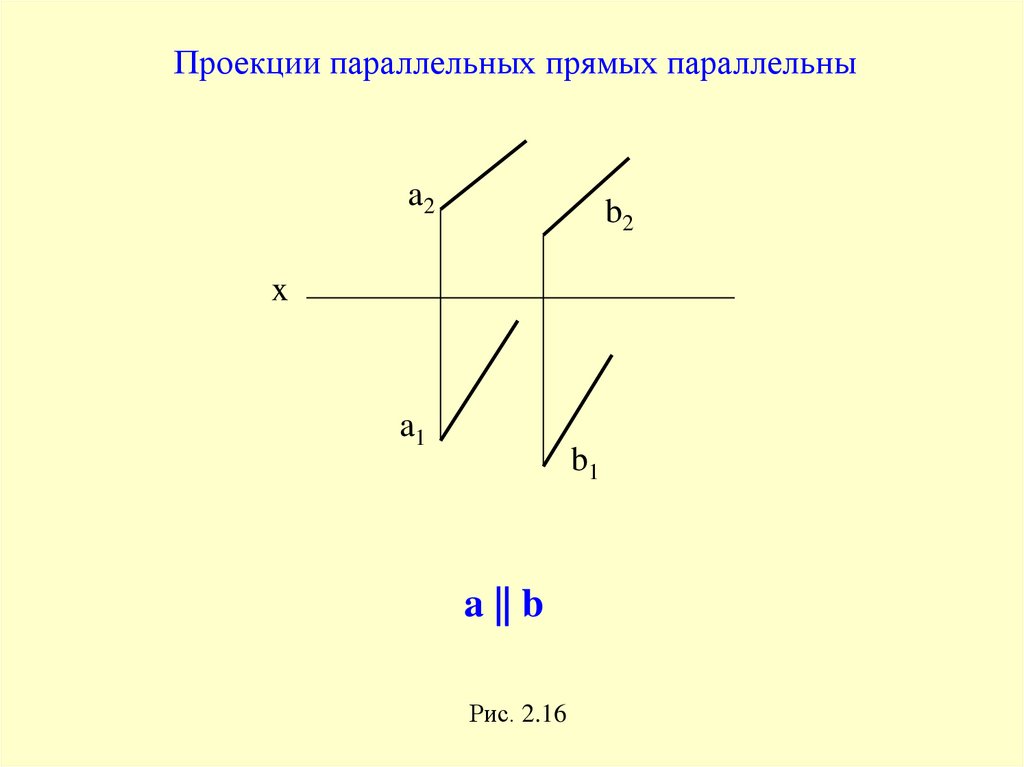
Проекции параллельных прямых параллельны.
3.
Если точка лежит на прямой, то и проекция этой
точки лежит на соответствующей проекции данной
прямой.
4.
Отношение отрезков проекции прямой равно
отношению отрезков прямой в пространстве (C1K1 :
K1D1 = CK : KD).
12.
Отсюда следует – для определенияпроекций прямой достаточно знать
проекции двух не тождественных
точек, принадлежащих прямой
13.
Прямая в системе двух прямоугольных проекцийВ2
а2
А2
х
О
В1
а1
А1
Рис. 2.2
14.
Прямоугольная изометрия прямойz
В
а
O
В1
А
а1
x
y
А1
Рис. 2.2
15.
Положение прямойотносительно плоскостей
проекций
16.
Прямая общего положения – прямая,не перпендикулярная ни одной из
плоскостей проекций
17.
Прямая общего положенияz
П2
В2
А2
x
В
П3
В3
Az
0 А3
Ах А
Аy
А1
П1
В1
y
Каждая из проекций отрезка прямой
меньше по величине самого отрезка
Рис. 2.3 а
18.
zВ2
В3
А2
А3
Аz
х
Ax
О
А1
В1
у
Рис. 2.3 б
у
19.
Прямая уровня - прямая, параллельнаяодной плоскости проекций
20.
Горизонталь h - прямая, параллельная П1z
П2
x
h2
А2
B2
Z=const
А2
А
B
h Bx
0
Ax
А1
h1
B1
Ax
x
h2 B2
Bx
β
П1
А1
y
Н.В.[AB]
Рис. 2.4
h1 B
1
0
21.
Фронталь f - прямая, параллельная П2z
Н.В.[AB]
А2
А2 f
2
А
x
Ax
А1
B2
f
B
0
Аx
x
f1 B1
А1
П1
y
Рис. 2.5
f2
B2
Bx
f1
B1
0
y=const
П2
22.
Профильная прямая р - прямая, параллельная П3z
П2
В2
р2
А2
x
Ах=Вх
В
В3 П3
р
А
В1
р1
П1 А1
р3
А3
y
Рис. 2.6 а
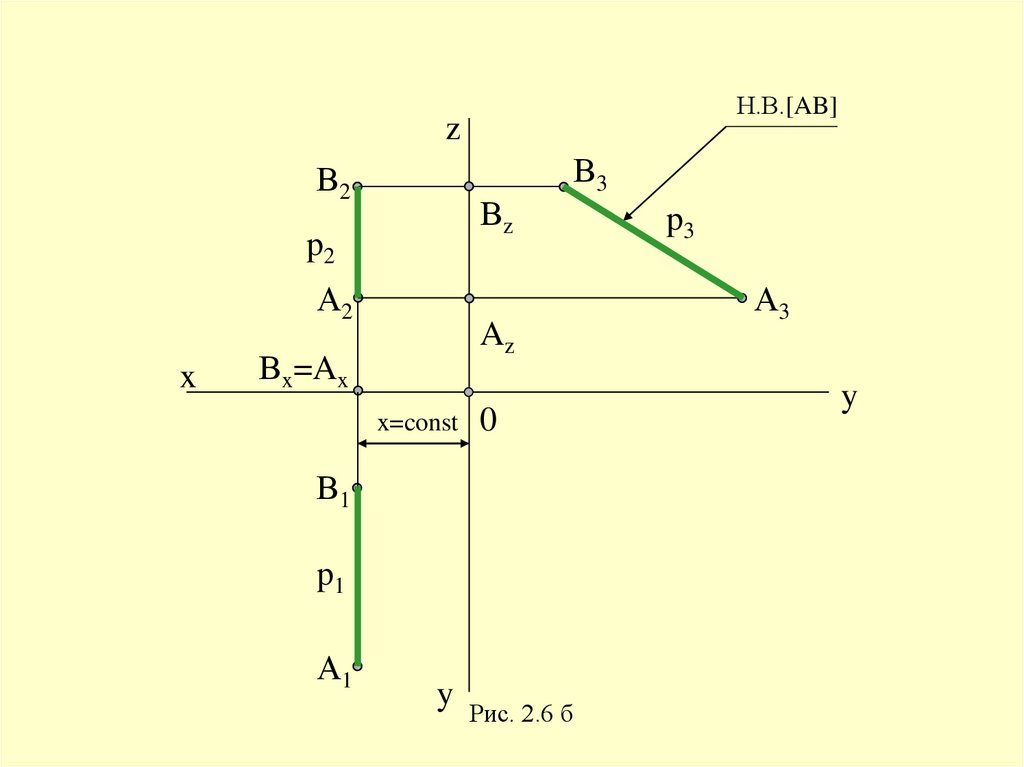
23.
Н.В.[AB]z
В2
Вz
p2
А2
x
Az
Вx=Ax
x=const
0
В1
p1
А1
y
Рис. 2.6 б
В3
p3
А3
y
24.
Вывод:Если отрезок лежит на прямой уровня
(прямой, параллельной одной плоскости
проекций), то он проецируется на
параллельную ему плоскость проекций в
натуральную величину,
а на две другие плоскости в виде отрезков
прямых, параллельных осям, образующим
данную плоскость проекций
25.
Проецирующие прямые - прямые,перпендикулярные одной из плоскостей
проекций
26.
Горизонтально-проецирующая прямая прямая, перпендикулярная П1z
П2
x
А2
А2
а2 А
B2
а
Аx=Bx
B
a2
B2
Аx=Bx
x
0
0
А1=B1=a1
П1
А1=B1 = a1
y
а1 - проекция-носитель или след-проекция
Рис. 2.7
27.
Фронтально-проецирующая прямая прямая, перпендикулярная П2z
П2
A2=B2 = a2
А2=B2=a2
x
Аx=Bx
B
a
А
a
B1 1
А1
Аx=Bx
x
0
0
B1
П1
Рис. 2.8
a1
y
А1
28.
Профильно-проецирующая прямая прямая, перпендикулярная П3z
П2
П3
A2 а2 B2
A
B
A3=B3=a3
а
x
0
а1
A1
B1
Рис. 2.9 а
П1
y
29.
zA2
a2 B2
A3=B3 = a3
x
0
a1
A1
B1
y
Рис. 2.9 б
y
30.
Вывод: Если прямая перпендикулярнакакой-нибудь плоскости проекций,
то на эту плоскость проекций она
проецируется в точку (след-проекция),
а две другие ее проекции перпендикулярны осям, образующим данную
плоскость проекций
31.
h0 П1x
h20
h10
h0 - нулевая горизонталь
Рис. 2.10 а
32.
f 0 П2f20
x
f10
f0 - нулевая фронталь
Рис. 2.10 б
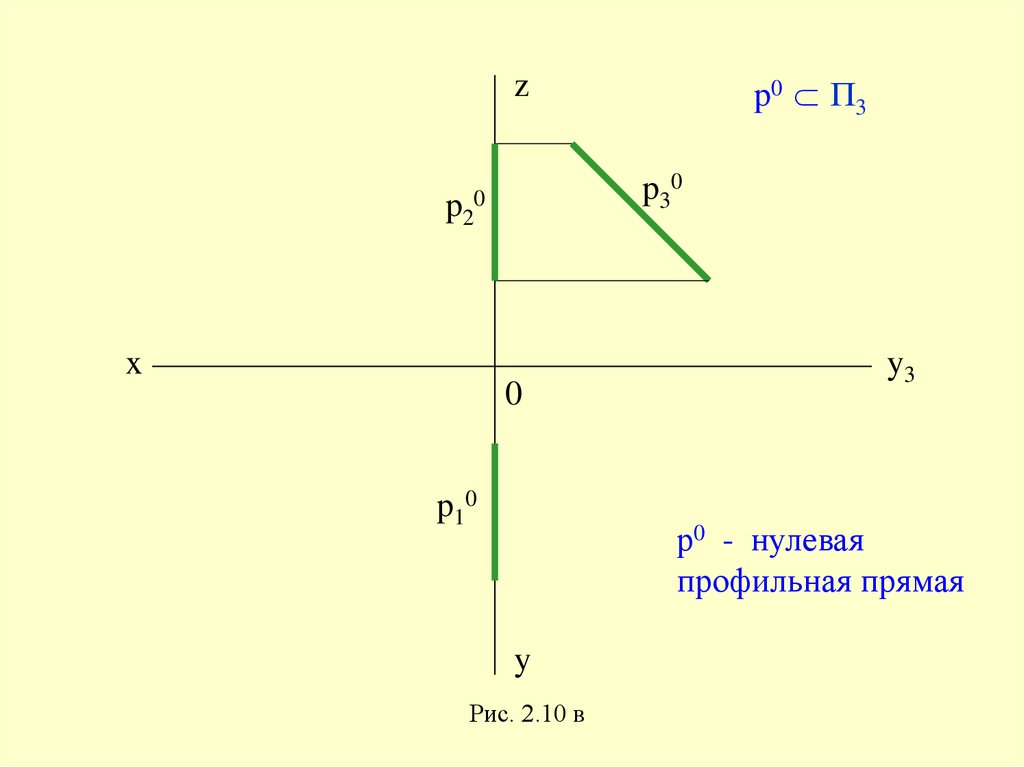
33.
p0 П3z
p2
p30
0
x
0
p10
y3
р0 - нулевая
профильная прямая
y
Рис. 2.10 в
34.
Точка на прямой35.
Точка принадлежит прямой,если проекция этой точки
принадлежит проекции этой прямой
36.
Определить принадлежат ли точки А и В прямой аB2
A2
a2
x
A a ,
A1
B1
a1
В a ,
т.к. В1 a1
т.к. А2 a2 , А1 а1
Рис.2.11
37.
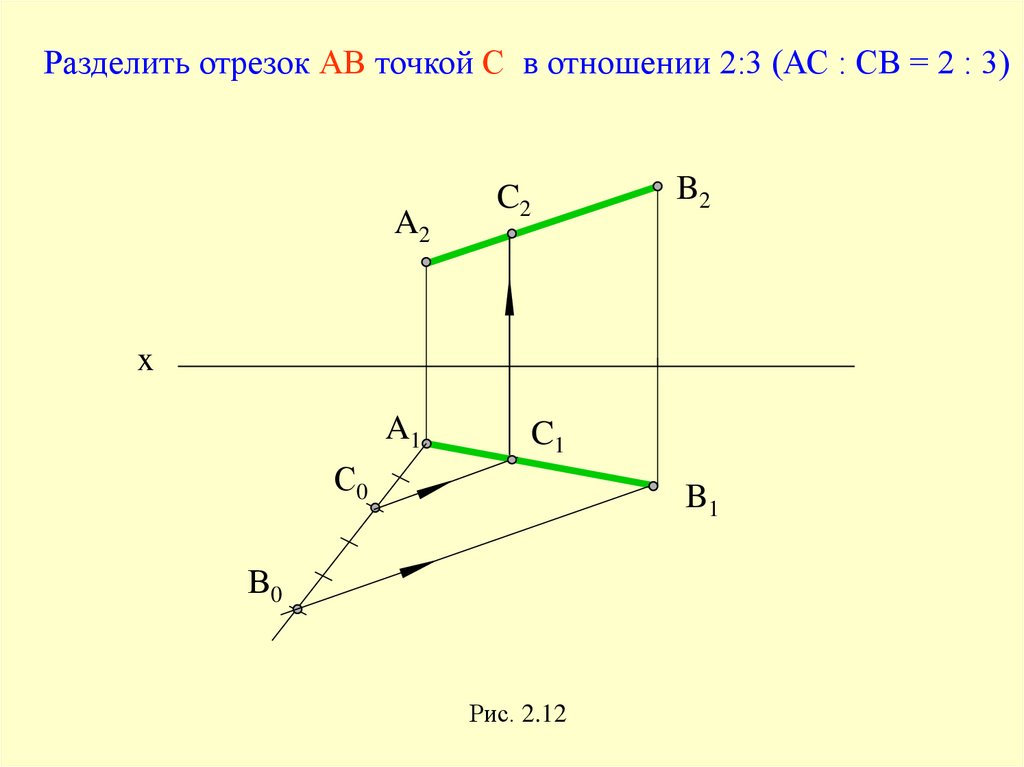
Разделить отрезок АВ точкой С в отношении 2:3 (АС : СВ = 2 : 3)A2
B2
C2
x
A1
C1
С0
B1
В0
Рис. 2.12
38.
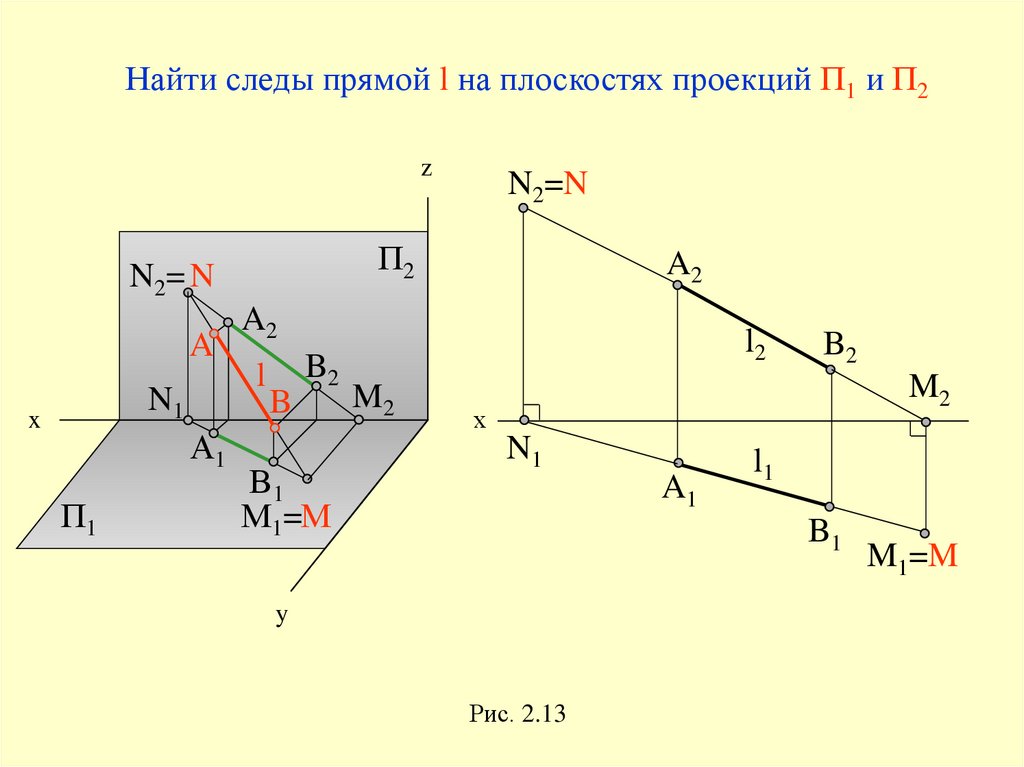
Следы прямой39.
Точки пересечения прямой линиис координатными плоскостями проекций
называются следами прямой
40.
Найти следы прямой l на плоскостях проекций П1 и П2z
П2
N2= N
A
N1
x
А1
П1
N2=N
A2
A2
l
B
B2
В1
М1=М
l2
M2
B2
M2
х
N1
A1
l1
B1
y
Рис. 2.13
M1=M
41.
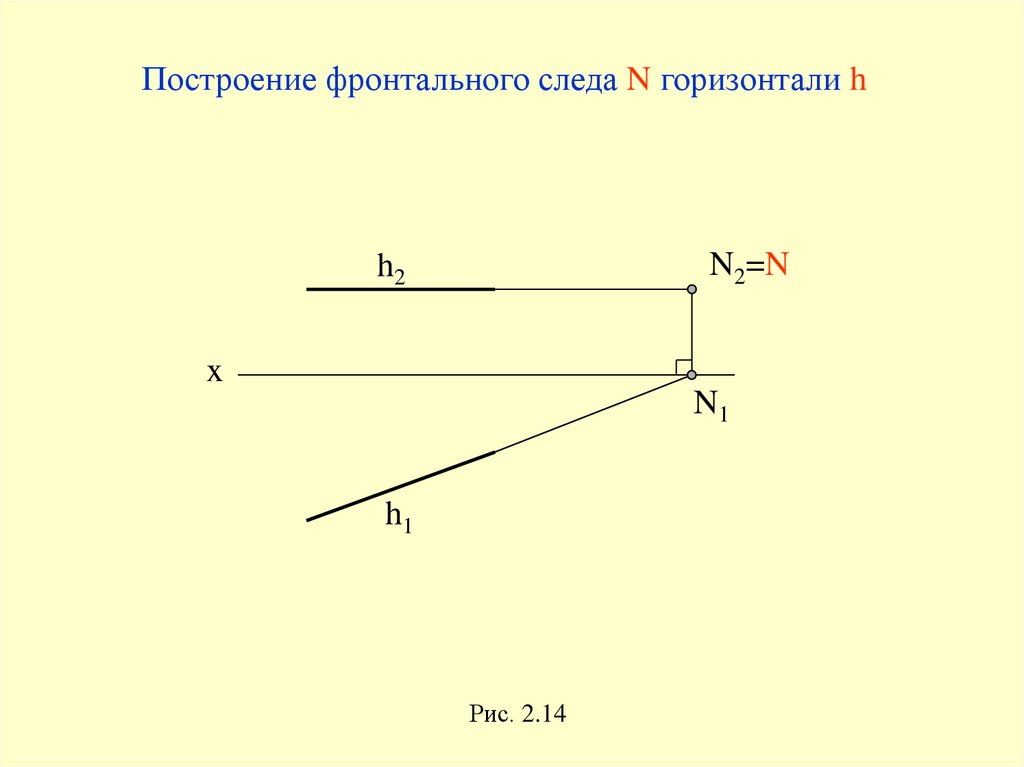
Построение фронтального следа N горизонтали hN2=N
h2
x
N1
h1
Рис. 2.14
42.
Взаимное положение прямых43.
Если прямые линии пересекаются, то их одноименныепроекции пересекаются между собой в точке, которая
является проекцией точки пересечения этих прямых
A2
x
b2
a2
A1
a1
a b
Рис. 2.15
b1
44.
Проекции параллельных прямых параллельныa2
b2
x
a1
b1
a || b
Рис. 2.16
45.
Скрещивающиеся прямыеa2
b2
x
a1
b1
a∸b
Рис. 2.17
46.
Плоские кривые47.
Кривые, все точки которыхпринадлежат одной плоскости,
называют плоскими
48.
Построение касательной t и нормали n к плоской кривой mM
t
m
M'
n
Рис. 2.18
Σ
49.
Если плоскость кривой перпендикулярна какой-либо плоскостипроекций, то на эту плоскость проекций кривая проецируется
в виде прямой
П2
С2
B2
x
l2
С2
A2
B2
А
Cx Ax С
0
l
Bx
В
B1
А1
l1 С1
П1
x
l2
Ах
Вх
Сх
B1
0
A1
l1
Рис. 2.19
A2
С1
50.
A2 C2=D2B2
x
D1
A1
B1
C1
Рис. 2.20
51.
D2A2=B2
C2
x
2R
B1
C1
D1
A1
Рис. 2.21
52.
4212
22
32
x
11
41
21
31
Рис. 2.22
53.
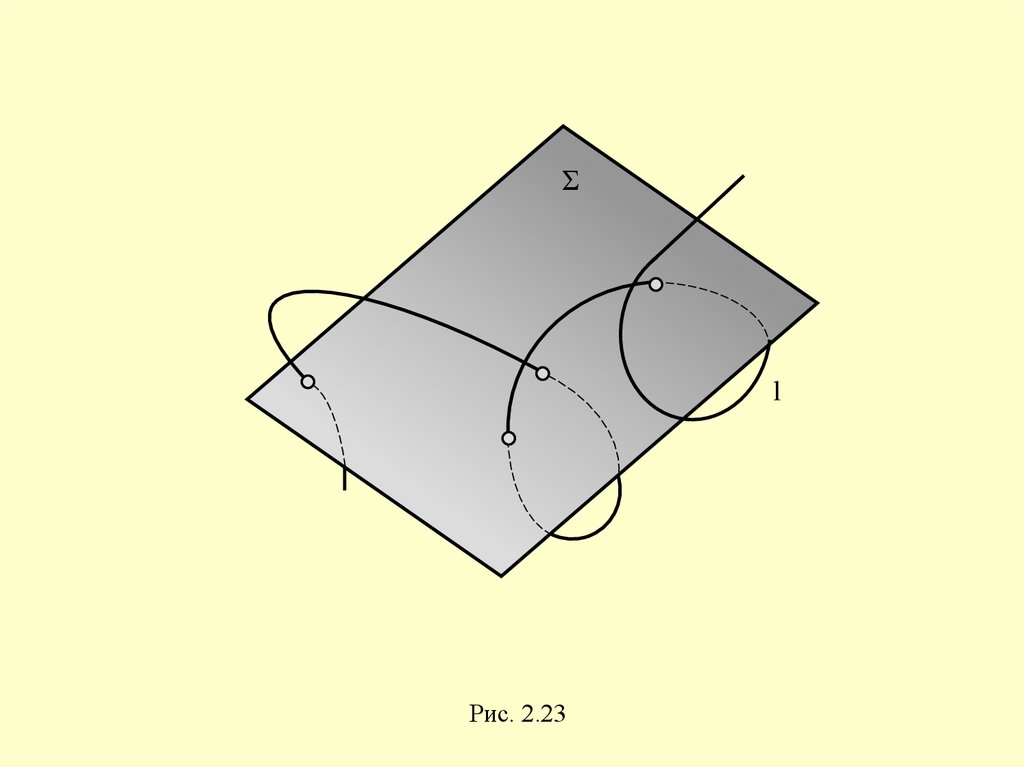
Пространственные кривые54.
Кривые, все точки которыхне принадлежат одной плоскости,
называются пространственными
55.
Σl
Рис. 2.23
56.
PО2
12
22
О1
11
21
Рис. 2.24















































 drafting
drafting








