Similar presentations:
Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости
1. Плоскость
Плоскость
Лекция № 3
2. План лекции
12
3
4
5
Задание плоскости на
чертеже
Точка и прямая в
плоскости
Положение плоскости в
пространстве
Главные линии
плоскости
Преобразование
чертежа плоскости
3.
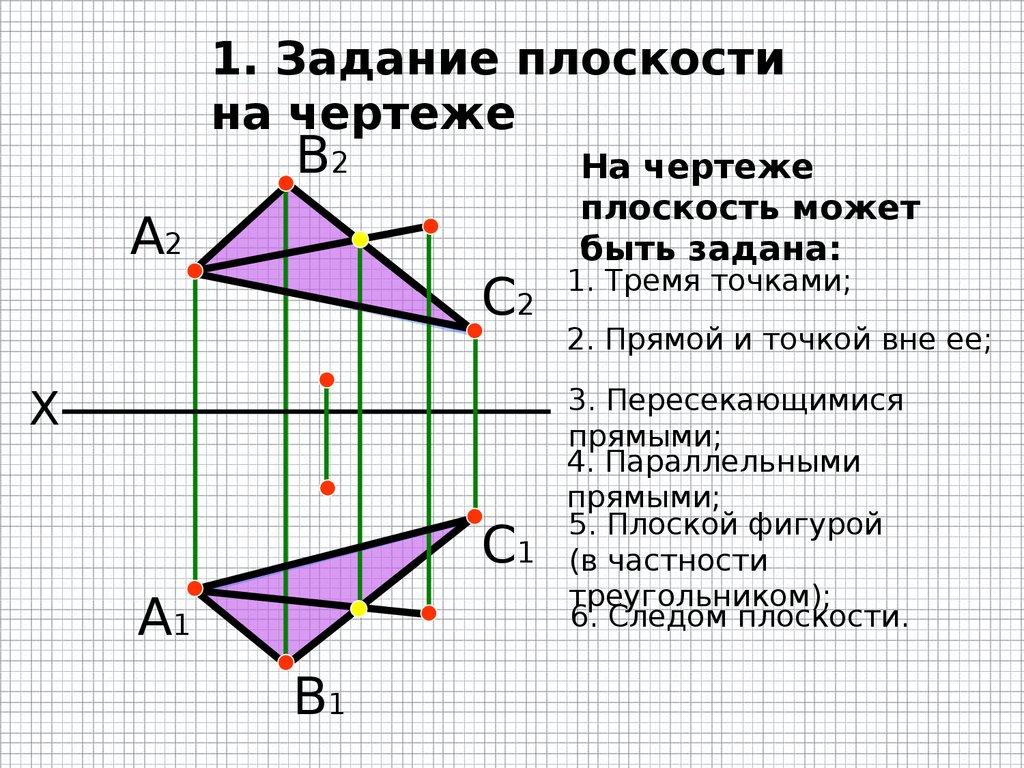
1. Задание плоскостина чертеже
В2
А2
С2
X
С1
А1
В1
На чертеже
плоскость может
быть задана:
1. Тремя точками;
2. Прямой и точкой вне ее;
3. Пересекающимися
прямыми;
4. Параллельными
прямыми;
5. Плоской фигурой
(в частности
треугольником);
6. Следом плоскости.
4.
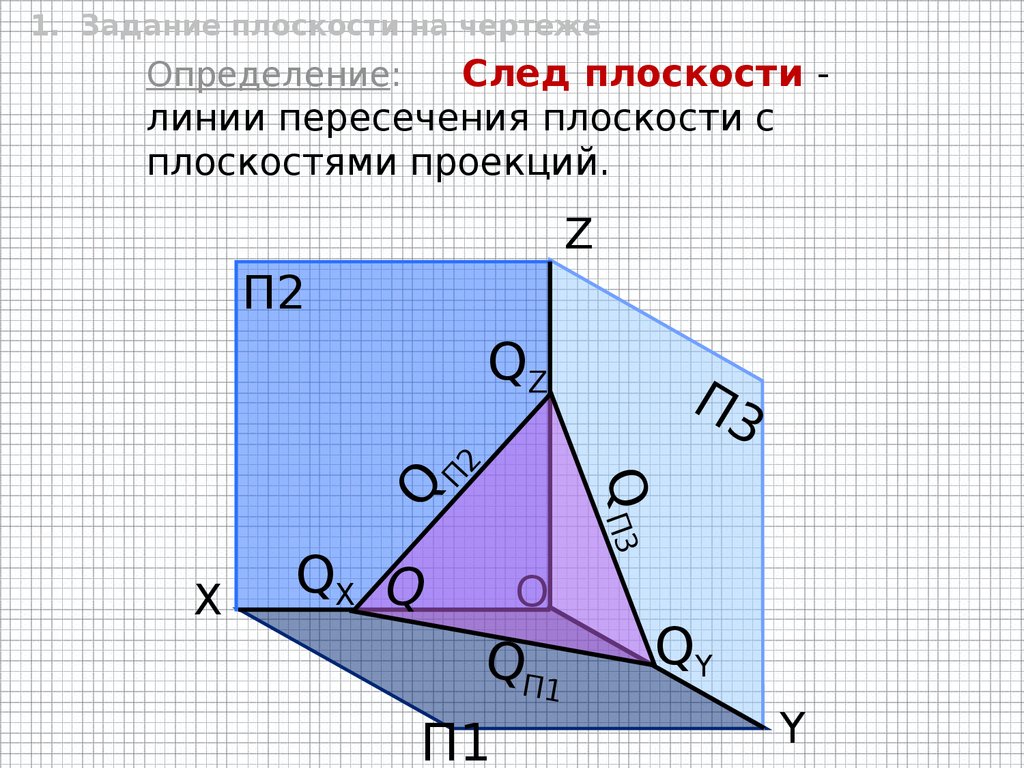
1. Задание плоскости на чертежеСлед плоскости линии пересечения плоскости с
плоскостями проекций.
Определение:
Z
П2
Q
X
П3
Q П3
П
2
QZ
QX Q
O
QП1
П1
QY
Y
5.
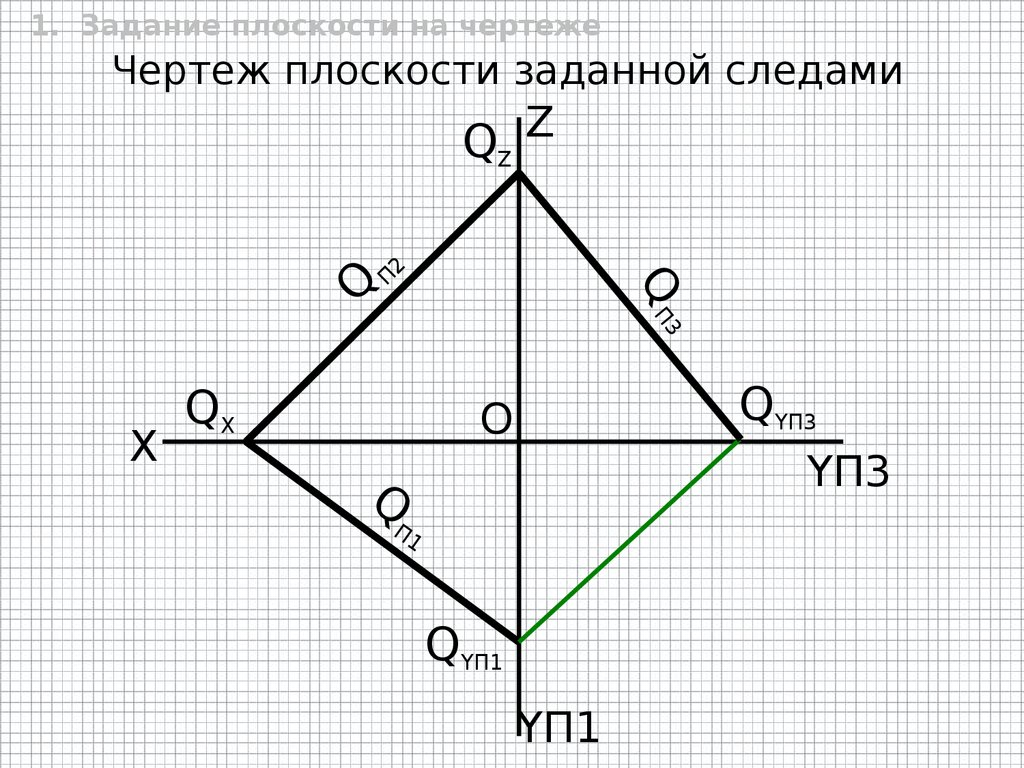
1. Задание плоскости на чертежеЧертеж плоскости заданной следами
QZ Z
3
QП
Q
2
П
X
QX
QYП3
O
YП3
Q
П1
QYП1
YП1
6.
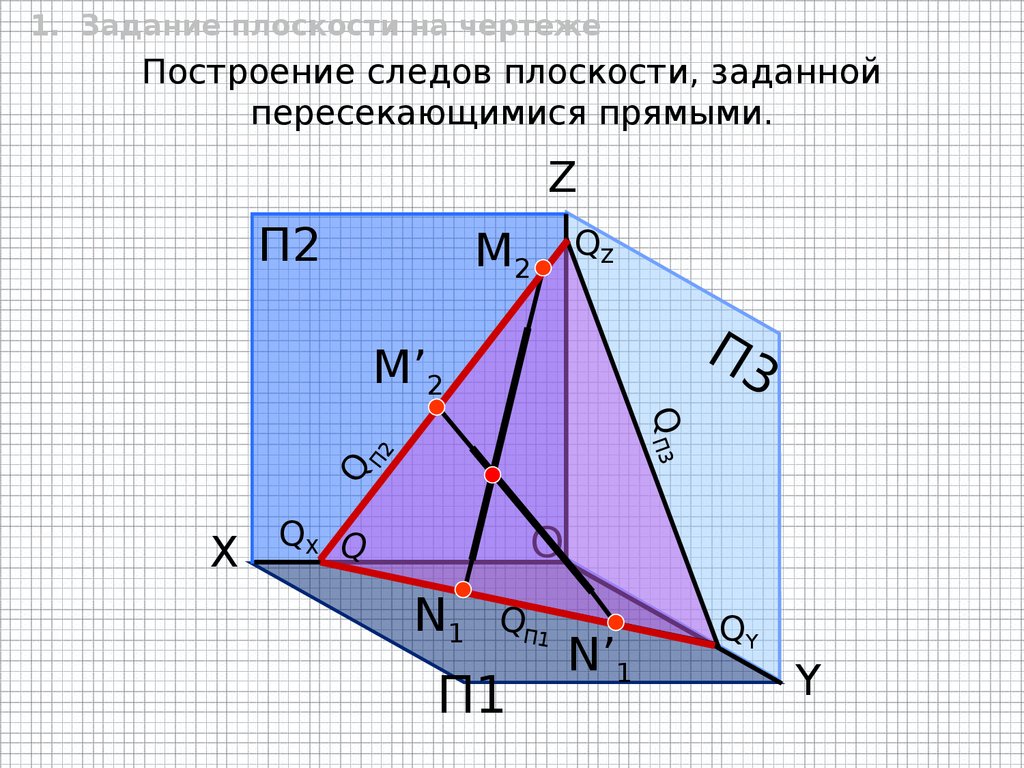
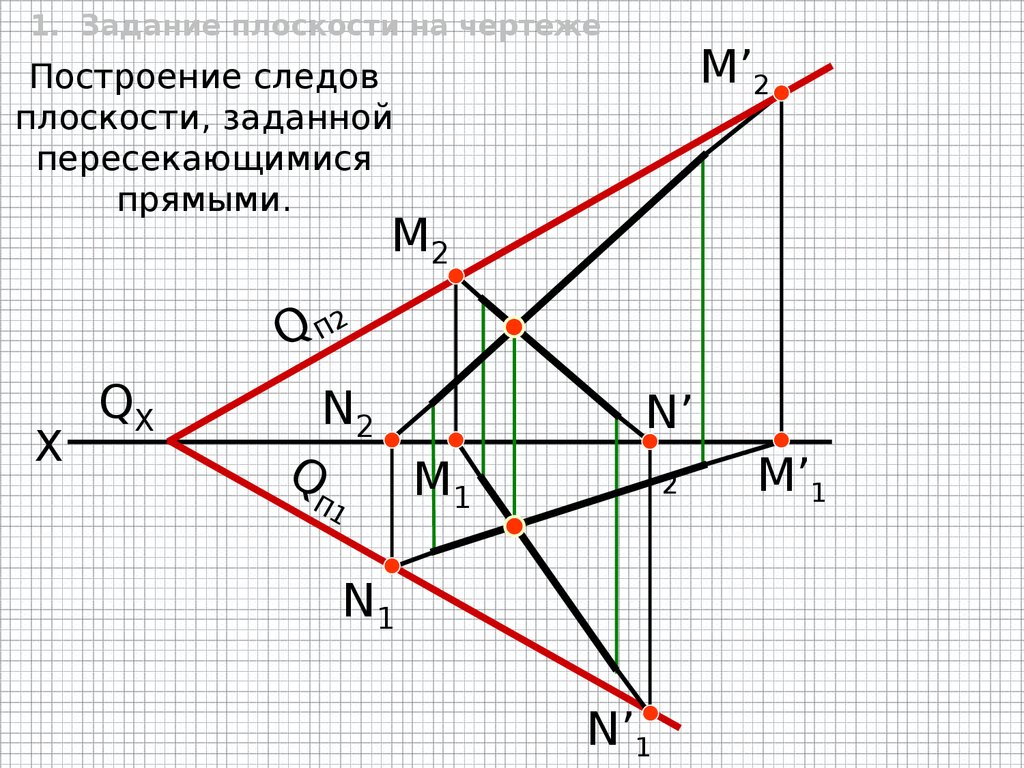
1. Задание плоскости на чертежеПостроение следов плоскости, заданной
пересекающимися прямыми.
Z
П2
M2
QZ
П3
M’2
Q
П2
Q П3
X
QX Q
O
N1
QП1
П1
N’1
QY
Y
7.
1. Задание плоскости на чертежеM’2
Построение следов
плоскости, заданной
пересекающимися
прямыми.
M2
Q П2
X
QX
Q
N2
N’
M1
П1
2
N1
N’1
M’1
8.
2. Точка и прямая вТочка принадлежит
плоскости, если она
плоскости
принадлежит какой-либо прямой, лежащей
в этой плоскости: т.K AB Q т.K Q.
Прямая принадлежит плоскости, если:
1) она проходит через две точки, лежащие в
данной плоскости: т.A Q т.B Q AB Q.
или
2) она проходит через точку, принадлежащую
плоскости, параллельно какой-нибудь прямой,
лежащей в этой плоскости:
т.A Q AB//CD CD Q AB Q.
9.
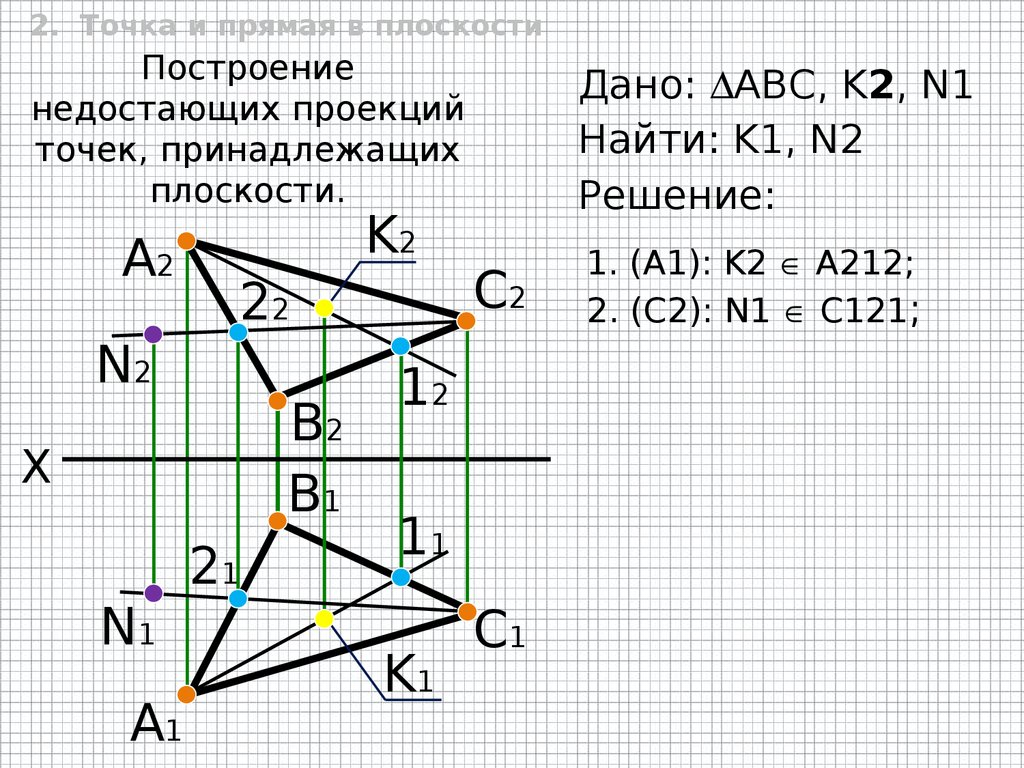
2. Точка и прямая в плоскостиПостроение
недостающих проекций
точек, принадлежащих
плоскости.
А2
K2
22
N2
В2
В1
X
21
N1
А1
Дано: АВС, K2, N1
Найти: K1, N2
Решение:
С2
12
11
K1
С1
1. (A1): K2 A212;
2. (C2): N1 C121;
10.
3. Положение плоскости впространстве
Плоскость, не параллельная и не
перпендикулярная
ни
одной
из
плоскостей
проекций,
называется
плоскостью общего положения.
Плоскости, параллельные
или
перпендикулярные плоскостям проекций,
называются
плоскостями
частного
положения.
11.
3. Положение плоскости в пространствеПлоскости частного положения
Проецирующие –
это плоскости
перпендикулярные
плоскости проекций
Уровня –
это плоскости
параллельные
плоскости проекций
Горизонтально- Профильно–
ГоризонтальныеПрофильные
–
проецирующие
–
роецирующие
–
это плоскости это плоскости
это плоскости это плоскости параллельные параллельные
перпендикулярные
ерпендикулярные
горизонтальной профильной
горизонтальной профильной
плоскости
плоскости проекций
П1 проекций
плоскости
скости проекций
П1 проекций П3
Фронтальнопроецирующие
–
это плоскости
перпендикулярные
фронтальной
плоскости проекций П2
Фронтальные –
это плоскости
параллельные
фронтальной
плоскости проекций П2
12.
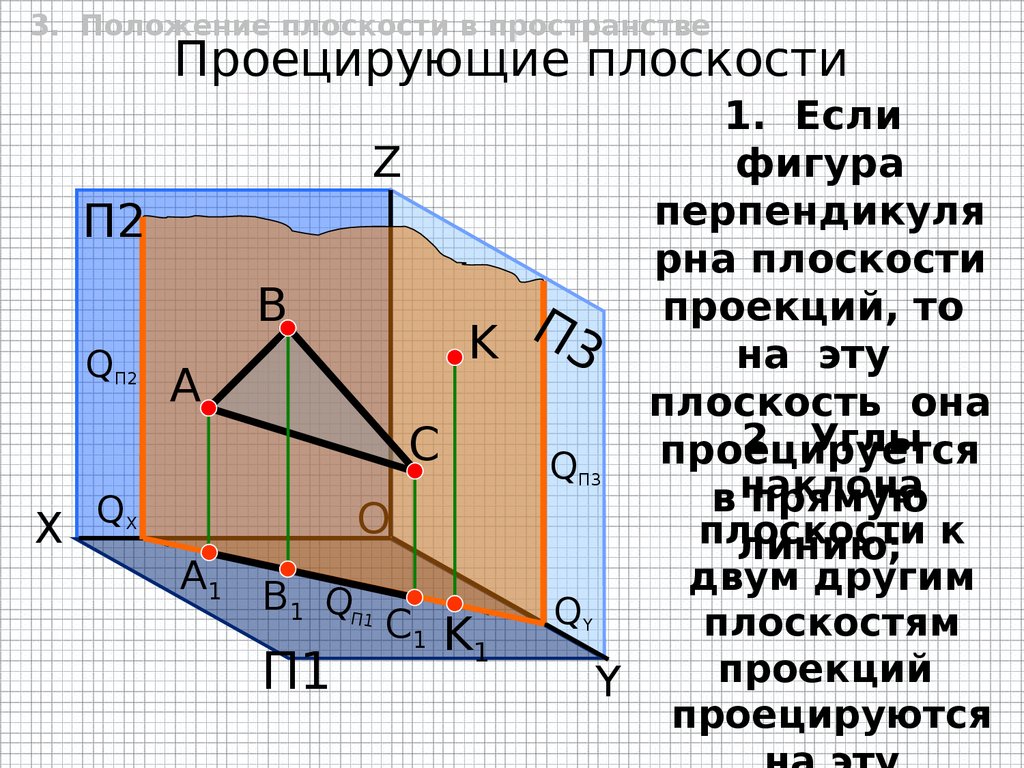
3. Положение плоскости в пространствеПроецирующие плоскости
П2
QП2
X
A
QX
A1
1. Если
Z
фигура
перпендикуля
рна плоскости
проекций, то
B
П
K 3
на эту
плоскость она
2. Углы
C
проецируется
QП3
в наклона
прямую
O
плоскости
линию; к
двум другим
B1 QП1
QY
плоскостям
C1 K
1
проекций
П1
Y
проецируются
13.
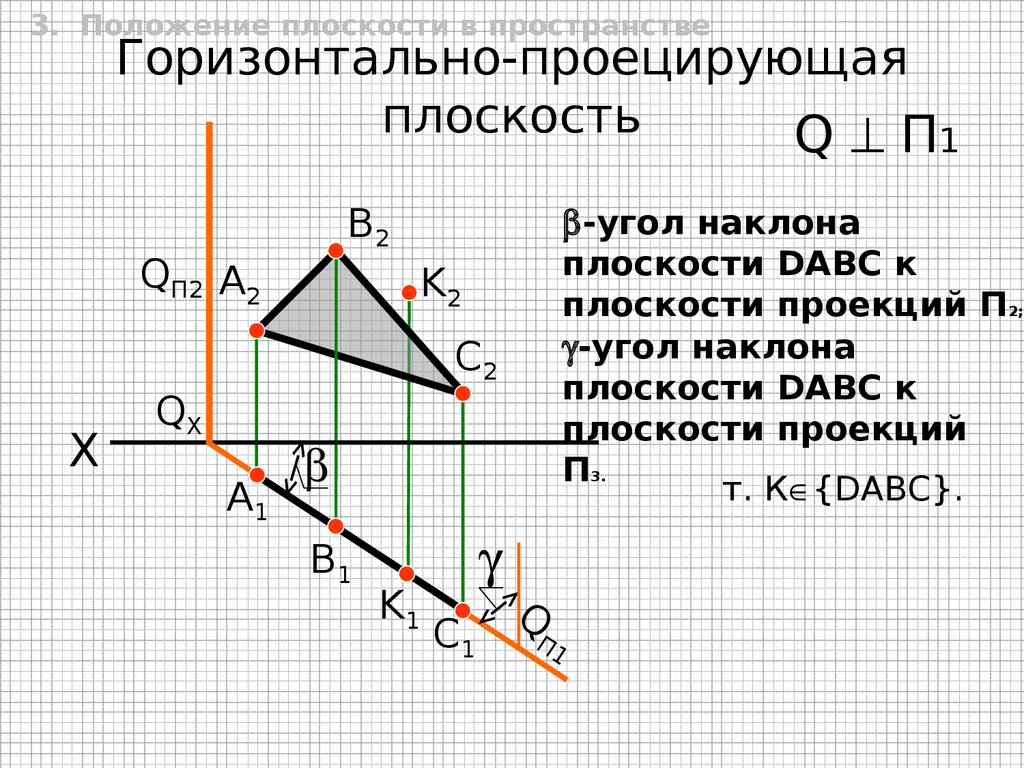
3. Положение плоскости в пространствеГоризонтально-проецирующая
плоскость
Q П1
-угол наклона
плоскости DАВС к
плоскости проекций П2;
-угол наклона
плоскости DАВС к
плоскости проекций
П3.
т. К {DАВС}.
B2
QП2 А2
K2
C2
X
QX
A1
B1
K1
C1
Q
П1
14.
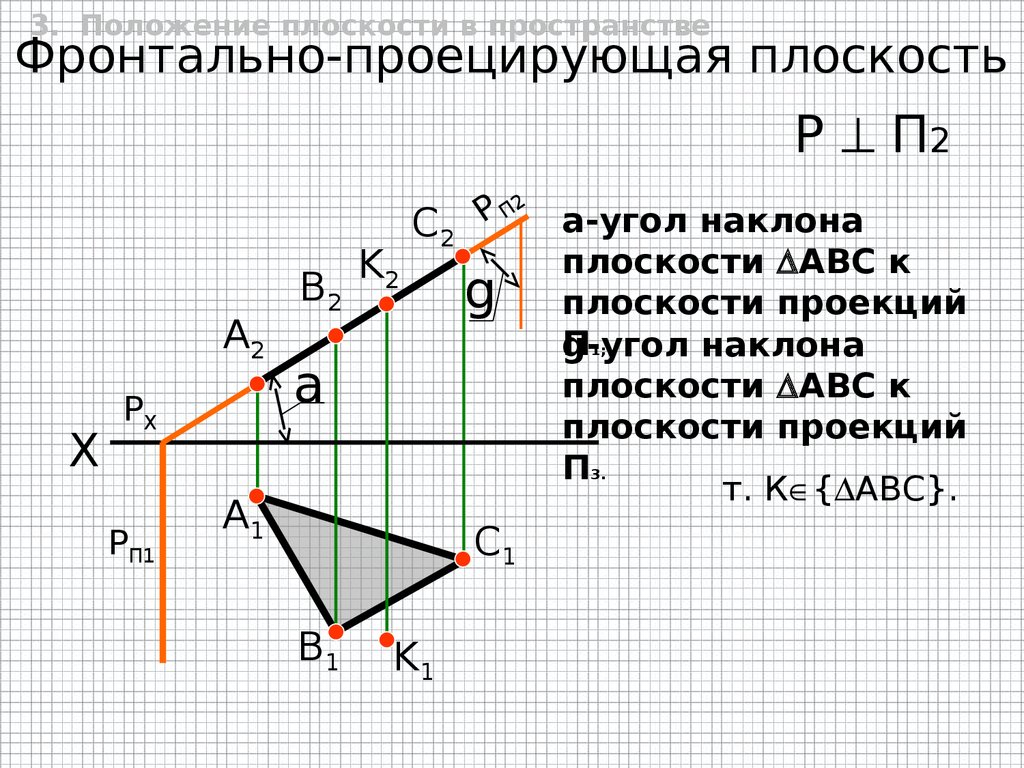
3. Положение плоскости в пространствеФронтально-проецирующая плоскость
P П2
А2
X
PX
PП1
B2
K2
C2
P П2
g
a
A1
C1
B1
K1
a-угол наклона
плоскости АВС к
плоскости проекций
П1;
g-угол
наклона
плоскости АВС к
плоскости проекций
П3.
т. К { АВС}.
15.
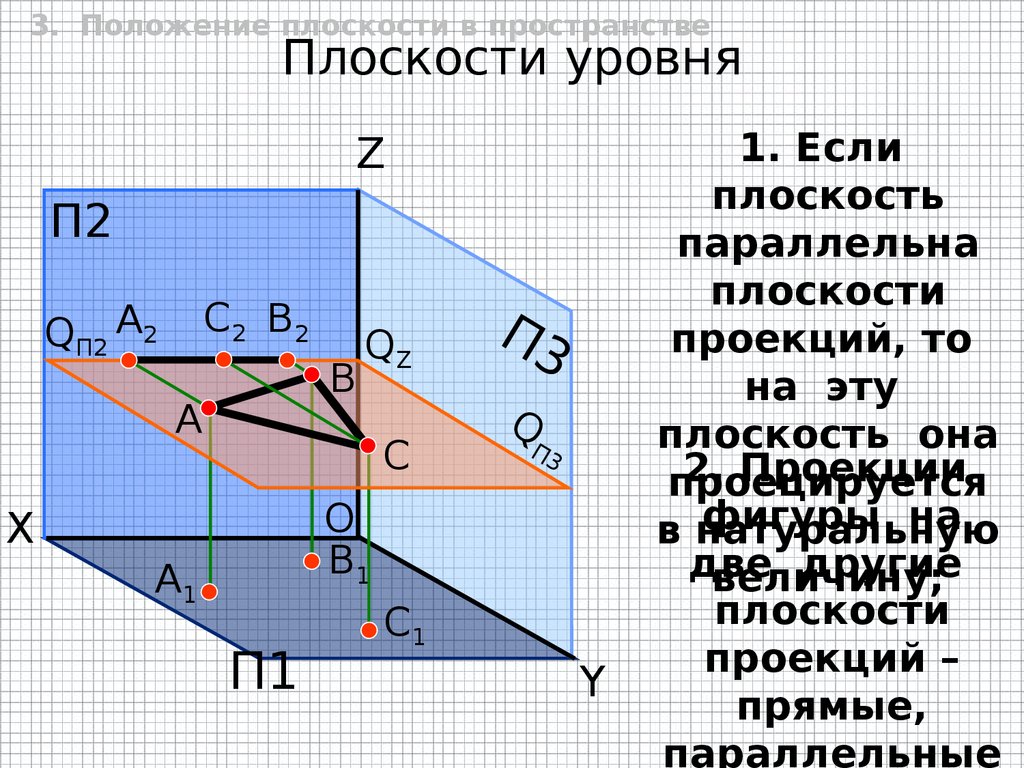
3. Положение плоскости в пространствеПлоскости уровня
Z
П2
С2 В2
QП2 A2
B
A
QZ
C
П3
Q
П3
O
B1
X
A1
П1
C1
Y
1. Если
плоскость
параллельна
плоскости
проекций, то
на эту
плоскость она
2. Проекции
проецируется
фигуры на
в натуральную
две
другие
величину;
плоскости
проекций –
прямые,
параллельные
16.
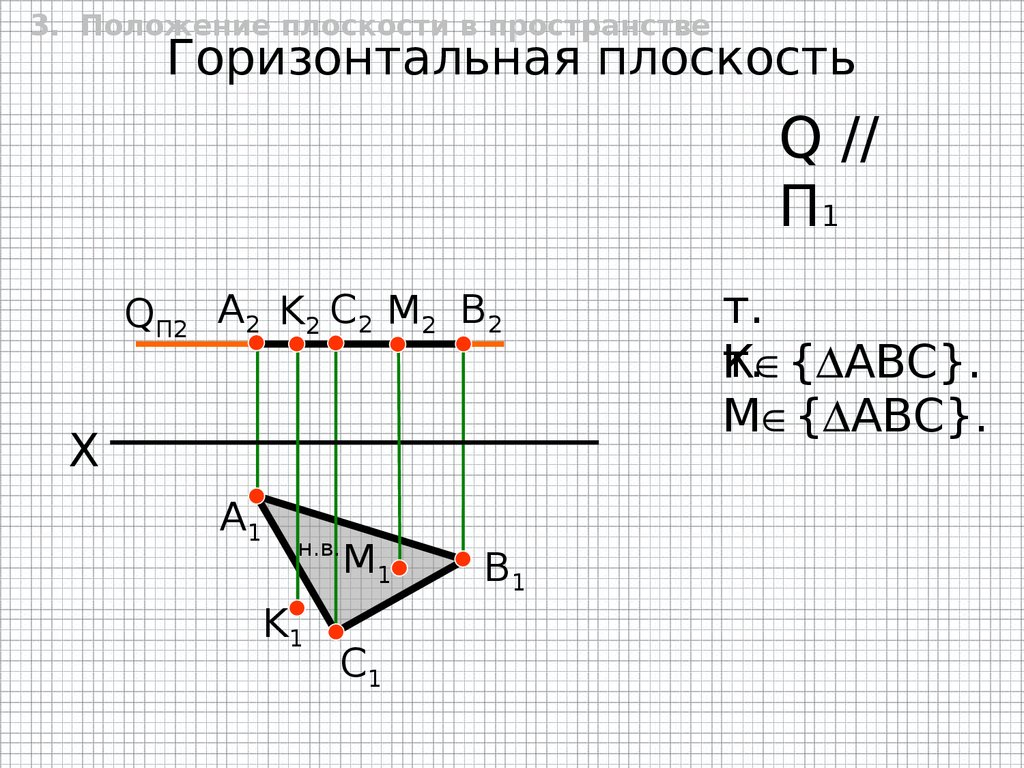
3. Положение плоскости в пространствеГоризонтальная плоскость
Q //
П1
QП2 А2 K2 C2 M2 B2
X
A1
н.в.
K1
M1
C1
B1
т.
т.
К { АВС}.
M { АВС}.
17.
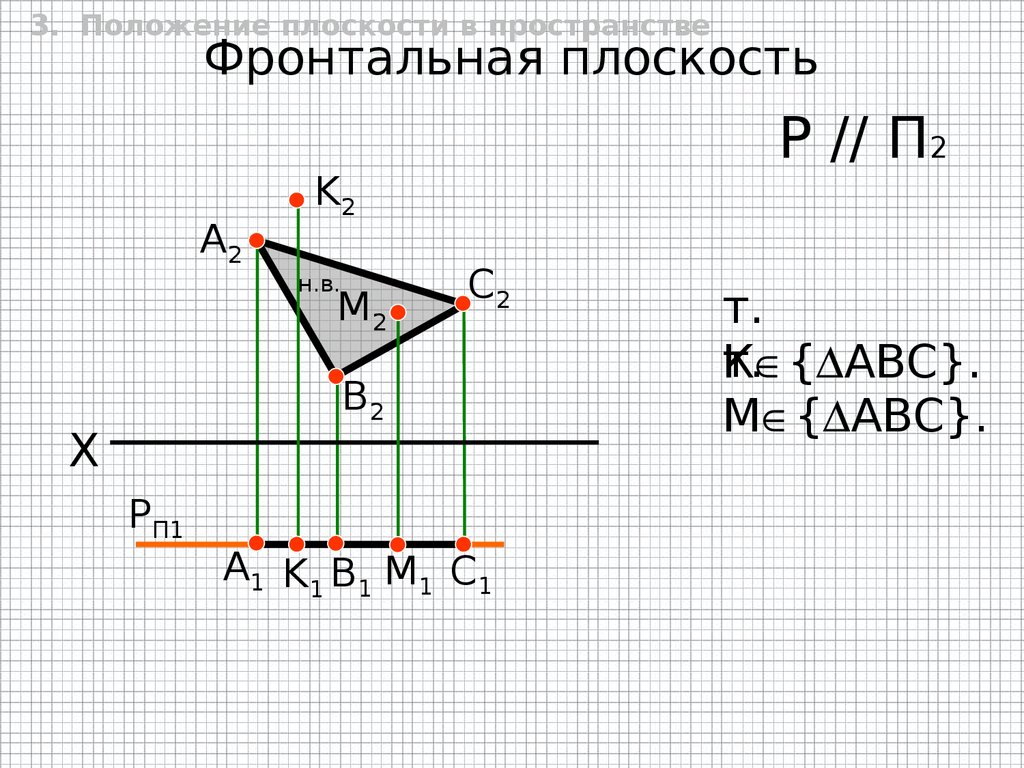
3. Положение плоскости в пространствеФронтальная плоскость
A2
Р // П2
K2
н.в.
M2
C2
B2
X
РП1
А1 K1 B1 M1 C1
т.
т.
К { АВС}.
M { АВС}.
18.
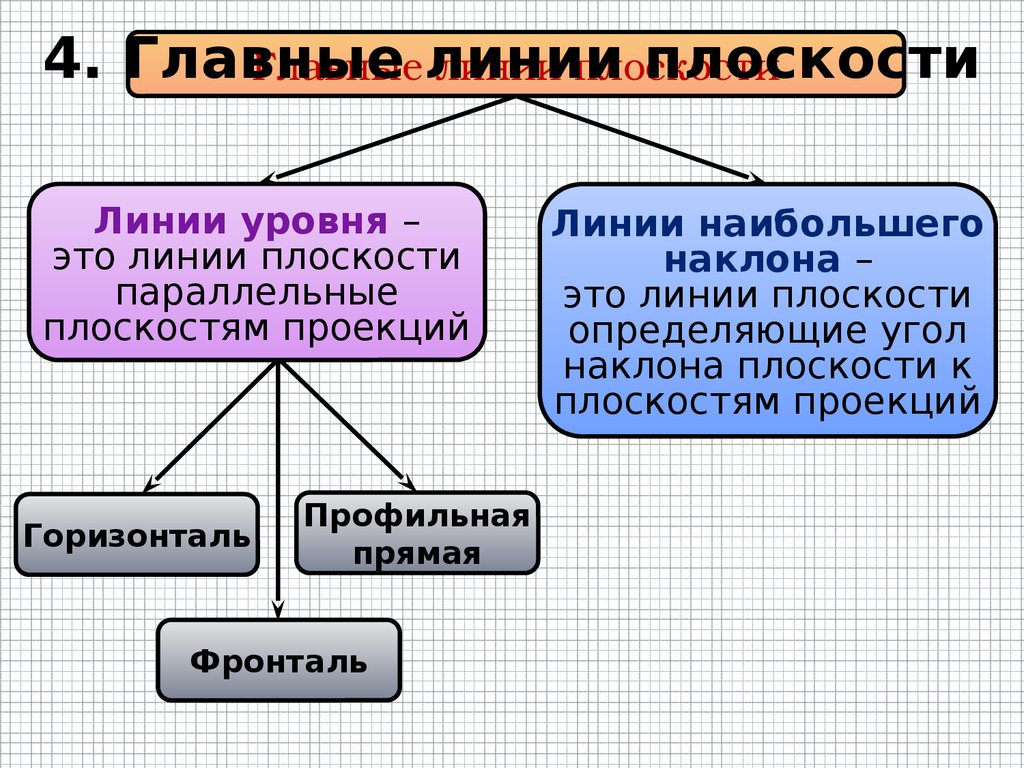
4. Главныелинии плоскости
Главные линии плоскости
Линии уровня –
это линии плоскости
параллельные
плоскостям проекций
Горизонталь
Профильная
прямая
Фронталь
Линии наибольшего
наклона –
это линии плоскости
определяющие угол
наклона плоскости к
плоскостям проекций
19.
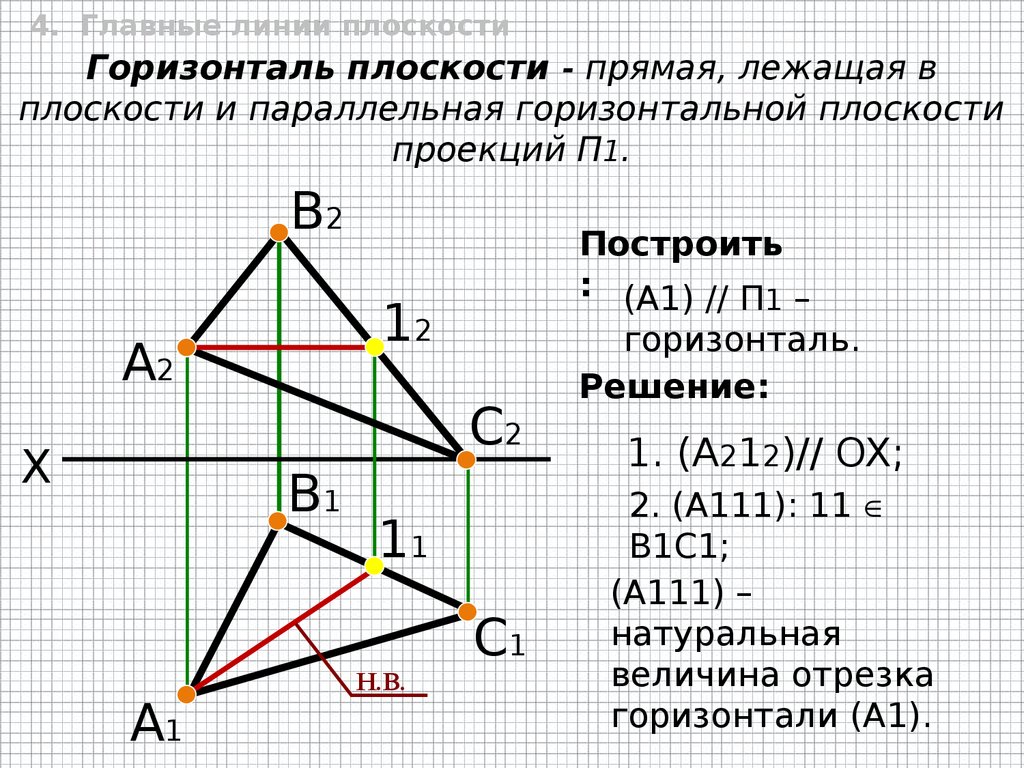
4. Главные линии плоскостиГоризонталь плоскости - прямая, лежащая в
плоскости и параллельная горизонтальной плоскости
проекций П1.
В2
Построить
: (A1) // П1 –
12
А2
С2
X
В1
11
С1
А1
Н.В.
горизонталь.
Решение:
1. (A212)// OX;
2. (A111): 11
В1С1;
(A111) –
натуральная
величина отрезка
горизонтали (А1).
20.
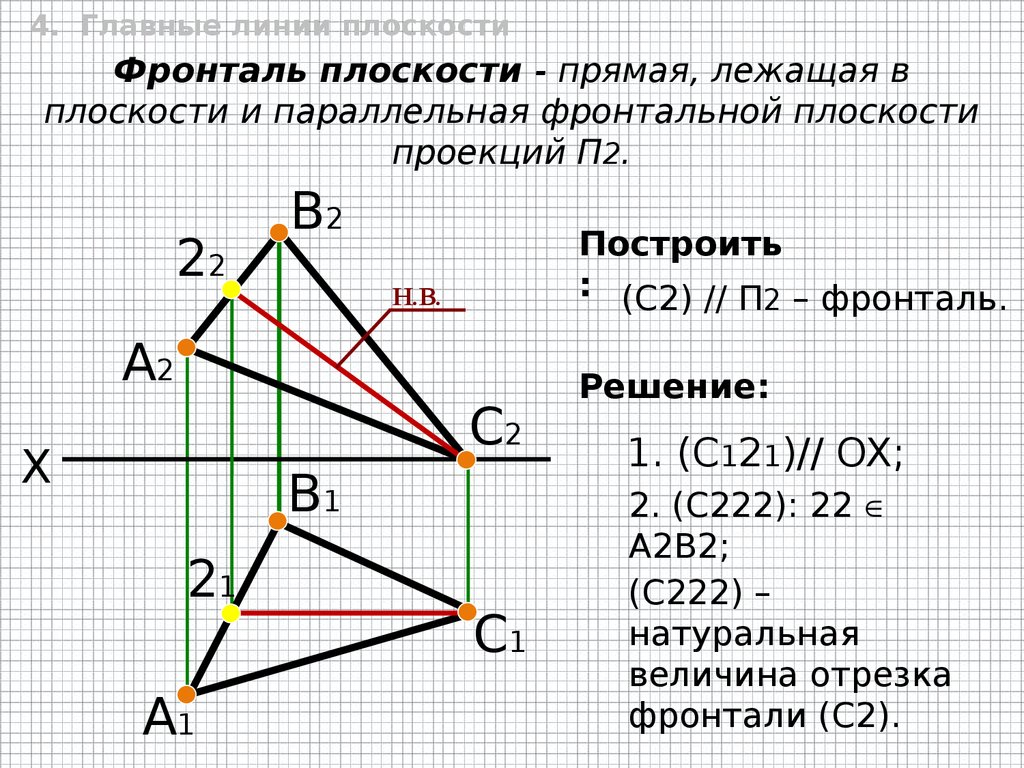
4. Главные линии плоскостиФронталь плоскости - прямая, лежащая в
плоскости и параллельная фронтальной плоскости
проекций П2.
22
В2
Построить
: (С2) // П2 – фронталь.
Н.В.
А2
С2
X
В1
21
А1
С1
Решение:
1. (С121)// OX;
2. (С222): 22
А2В2;
(С222) –
натуральная
величина отрезка
фронтали (С2).
21.
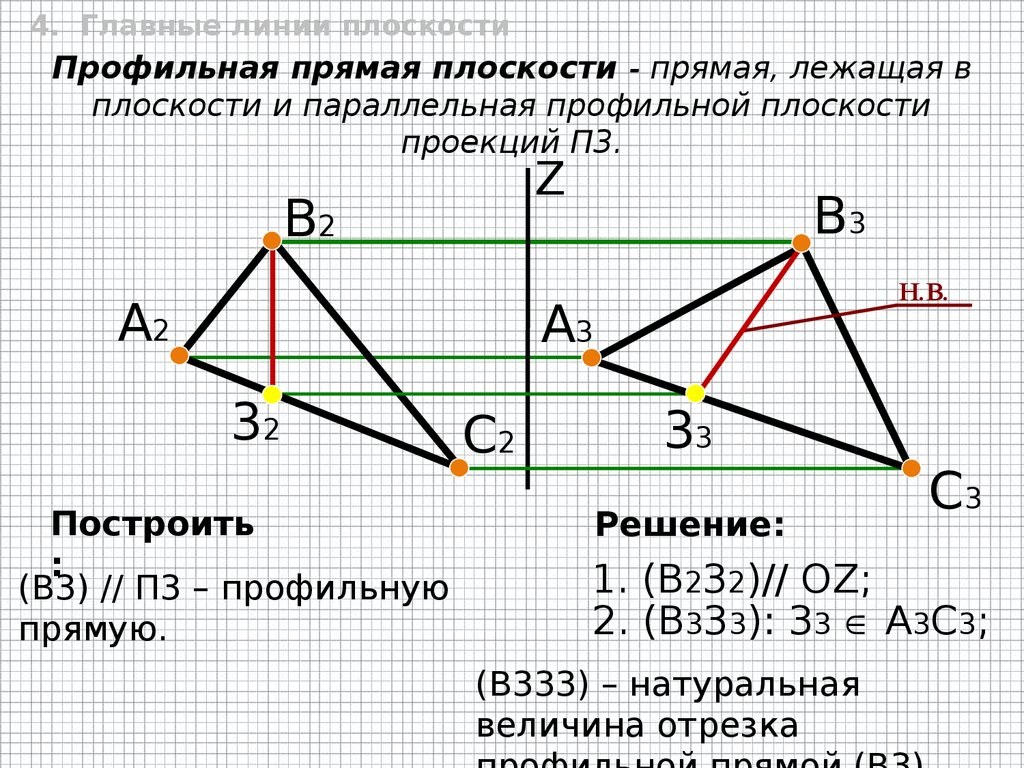
4. Главные линии плоскостиПрофильная прямая плоскости - прямая, лежащая в
плоскости и параллельная профильной плоскости
проекций П3.
Z
В2
А2
В3
Н.В.
А3
32
Построить
:
(B3) // П3 – профильную
прямую.
С2
33
Решение:
С3
1. (В232)// OZ;
2. (B333): 33 А3C3;
(B333) – натуральная
величина отрезка
22.
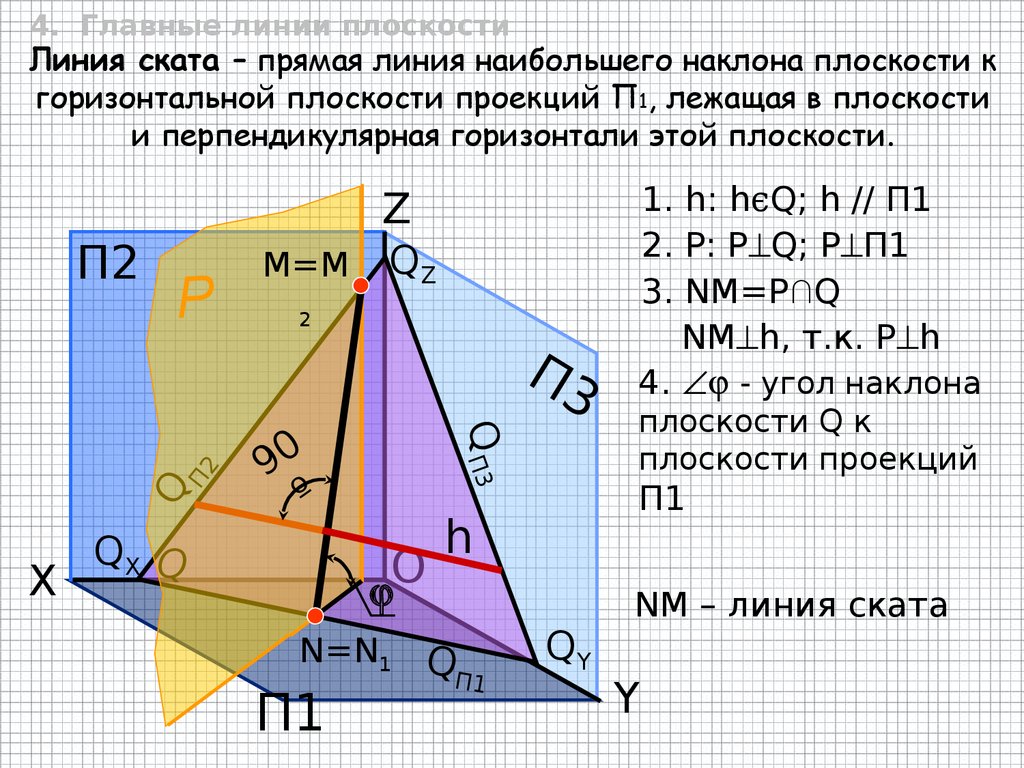
4. Главные линии плоскостиЛиния ската – прямая линия наибольшего наклона плоскости к
горизонтальной плоскости проекций П1, лежащая в плоскости
и перпендикулярная горизонтали этой плоскости.
Z
П2
P
M=M
QZ
2
Q
Q П3
П2
П3
90
º
QX Q
X
O
П1
1
плоскости Q к
плоскости проекций
П1
h
N=N1 Q
П
1. h: hϵQ; h // П1
2. Р: P Q; P П1
3. NM=P∩Q
NM h, т.к. Р h
4. - угол наклона
QY
NM – линия ската
Y
23.
5. Преобразование чертежаплоскости
Плоскость общего
положения может быть
преобразована в:
1. проецирующую
плоскость;
2. плоскость уровня.
24.
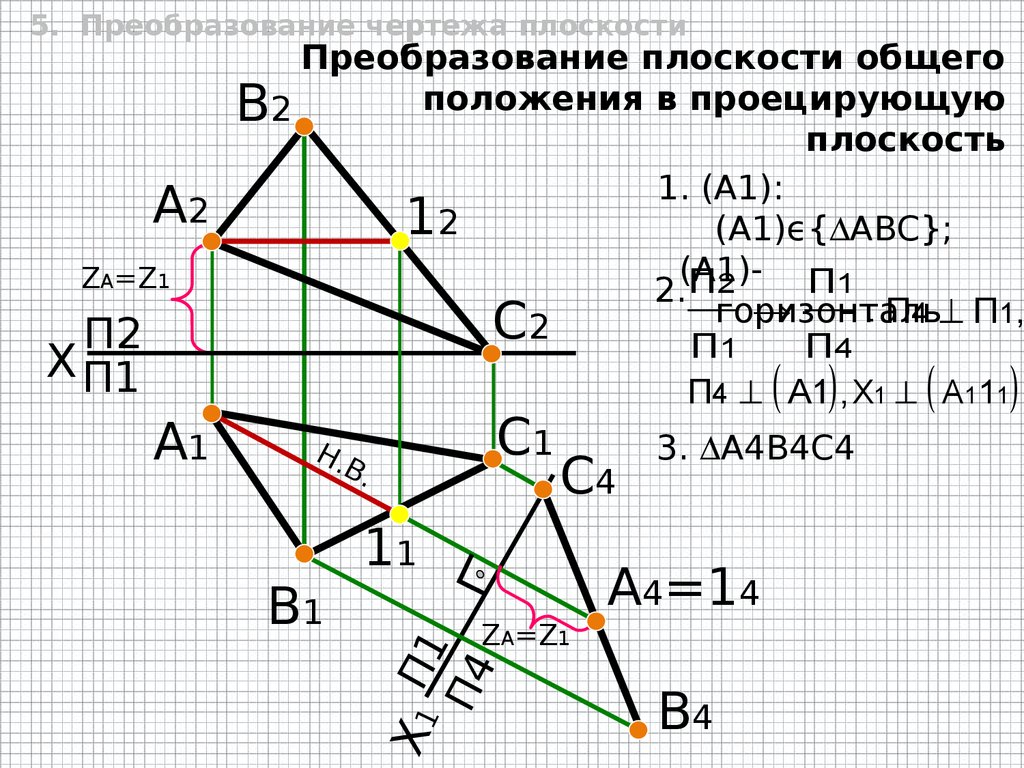
5. Преобразование чертежа плоскостиПреобразование плоскости общего
положения в проецирующую
В2
плоскость
1. (A1):
А2
12
(A1)ϵ{ ABC};
(A1)ZА=Z1
П1
2. П2
: П4 П1 ,
горизонталь
С
2
П2
П1
П4
X П1
П4 A1 , X1 А111
С
1
А1
3. A4B4C4
Н.
В.
С4
А4=14
ZА=Z1
П4
Х1 П1
В1
11
В4
25.
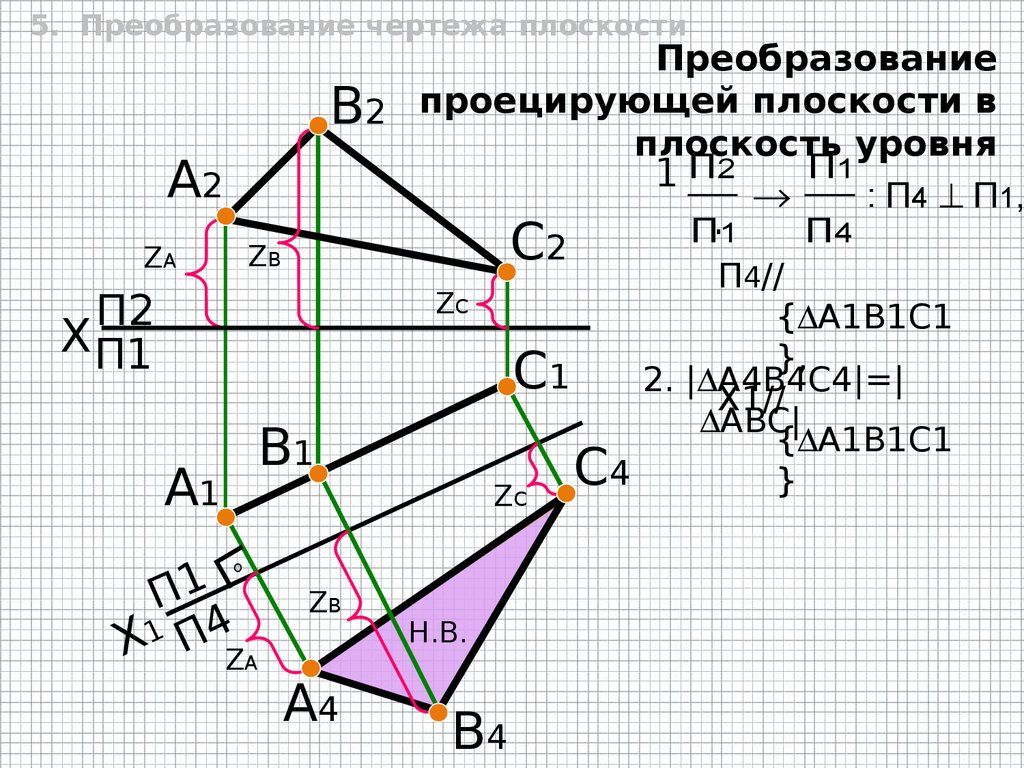
5. Преобразование чертежа плоскостиПреобразование
В2 проецирующей плоскости в
плоскость уровня
П1
1 П2
А2
: П4 П1 ,
.1
П
П4
С
2
ZB
ZА
П4//
ZC
П2
{ A1B1C1
X П1
},
С1 2. | A4B4C4|=|
Х1//
ABC|
{ A1B1C1
В1
С4
}
А1
ZC
П1
Х1 П4ZА
ZB
А4
Н.В.
В4
26.
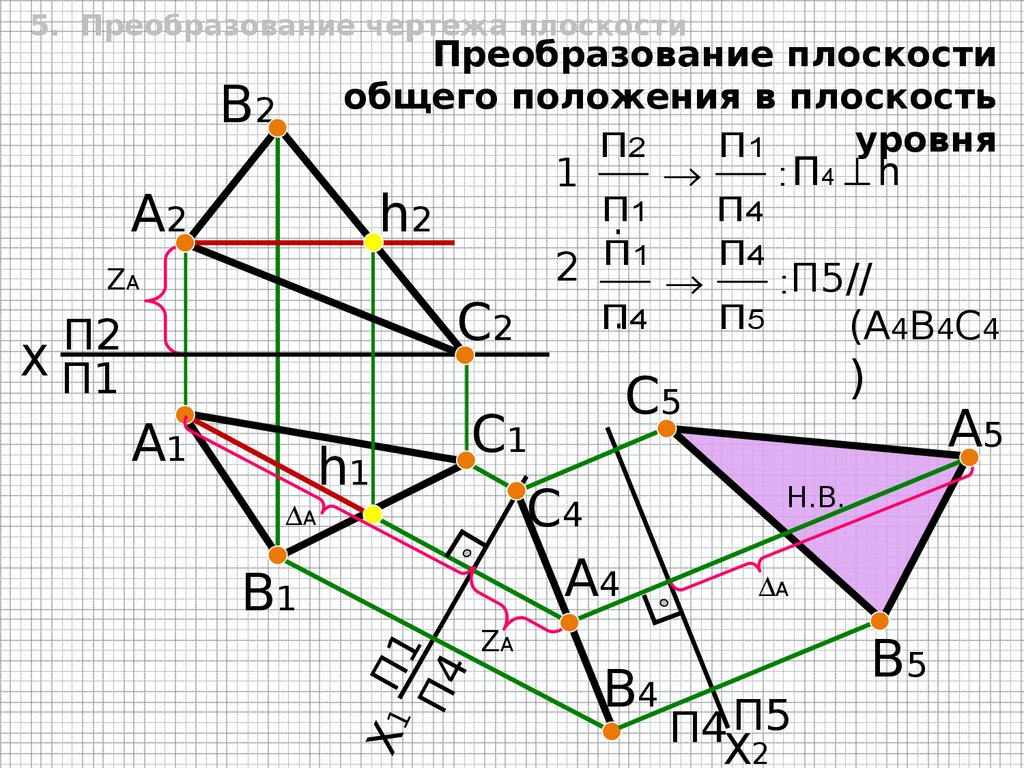
5. Преобразование чертежа плоскостиПреобразование плоскости
общего положения в плоскость
уровня
П2
П1
: П4 h
1
П
П4
h2
.1
2 П1 П4 :П5//
.4
П
П5
(A4B4C4
С2
В2
А2
ZА
П2
X П1
А1
h1
А
Х1 П1
П4
В1
С1
С4
А4
)
C5
Н.В.
А
ZА
В4
А5
B5
П4 П5
Х2
27.
Авторы:доценты кафедры «Начертательная
геометрия, инженерная и компьютерная
графика» Омского Государственного
технического университета:
Бондарев Олег Александрович, к.т.н.,
Кайгородцева Наталья Викторовна,
к.пед.н.







 mathematics
mathematics drafting
drafting








